基于小样本条件的雷达辐射源个体识别算法

丁辰伟，孙闽红，官友廉

(1 杭州电子科技大学通信工程学院，杭州 310000;2 75798部队，北京 100089)

0 引言

特定辐射源识别(special emitter identification, SEI)是通过分析从辐射源发送的信号中提取与辐射源设备相关联的特征参数(个体细微特征)来自动识别辐射源的技术。近年来，人工智能技术迅速发展，深度学习算法被广泛应用于辐射源个体识别。文献[1]提出了一种利用CNN识别7种脉冲重复间隔调制类型的全自动方法，不仅提高了系统的性能，而且对具有丢失和伪脉冲的环境具有鲁棒性；文献[2]构建了一个深度残差网络来学习信号的希尔伯特谱图，有效解决了退化问题，提高了效率和通用性；文献[3]采用卷积神经网络对特定辐射源信号进行压缩双谱识别，提高了识别性能；文献[4]提出了一种基于稀疏自编码器(SAE)的电磁信号分类算法。但是，上述算法都忽略了特征间的内在联系。在图像识别中往往会采用图像增强技术[5-6]对图像进行处理提高识别性能。但是，不论是传统方法还是深度学习方法，算法性能都受到样本数目的约束，在小样本的情况下算法很难达到较好的识别性能。文献[7]提出了一种多模态Weibull虚拟样本创建算法，使用一个数据集来检查所提出的方法的性能，并且通过预测均方根误差进行比较，验证了算法的有效性；文献[8]提出了一种分段随机抽样方法对加速测试数据进行重采样，有效扩展测试样本大小，并通过仿真验证了生成样本的可靠性；文献[9]提出了类似于原始图像的多个虚拟样本生成算法，提高了小样本下的识别率；文献[10]提出了一种基于增强条件对抗生成网络(SCGAN)和CNN的低分辨雷达目标识别算法，提高了小样本条件下算法的识别性能。

文中采用图像增强算法对SAE提取的特征进行特征增强，使得特征间的差异更加明显，然后利用SCGAN和CNN网络对增强后的特征进行训练识别，有效提高了小样本条件下雷达辐射源个体识别的识别率。

1 基于小样本条件的雷达辐射源个体识别算法

1.1 算法原理

如图1所示，算法流程为：

图1 算法运行框图

1)数据预处理。首先对接收到的雷达脉冲信号s(t)进行短时傅里叶变换(STFT)得到它的时频图矩阵S(t,f)；然后将时频图矩阵S(t,f)进行灰度处理得到灰度矩阵W；最后将灰度矩阵W进行向量化操作，得到一个N维向量v作为输入样本。将采集到的多个雷达辐射源下M个脉冲信号进行上述操作，得到一个大小为M×N的灰度矩阵V。

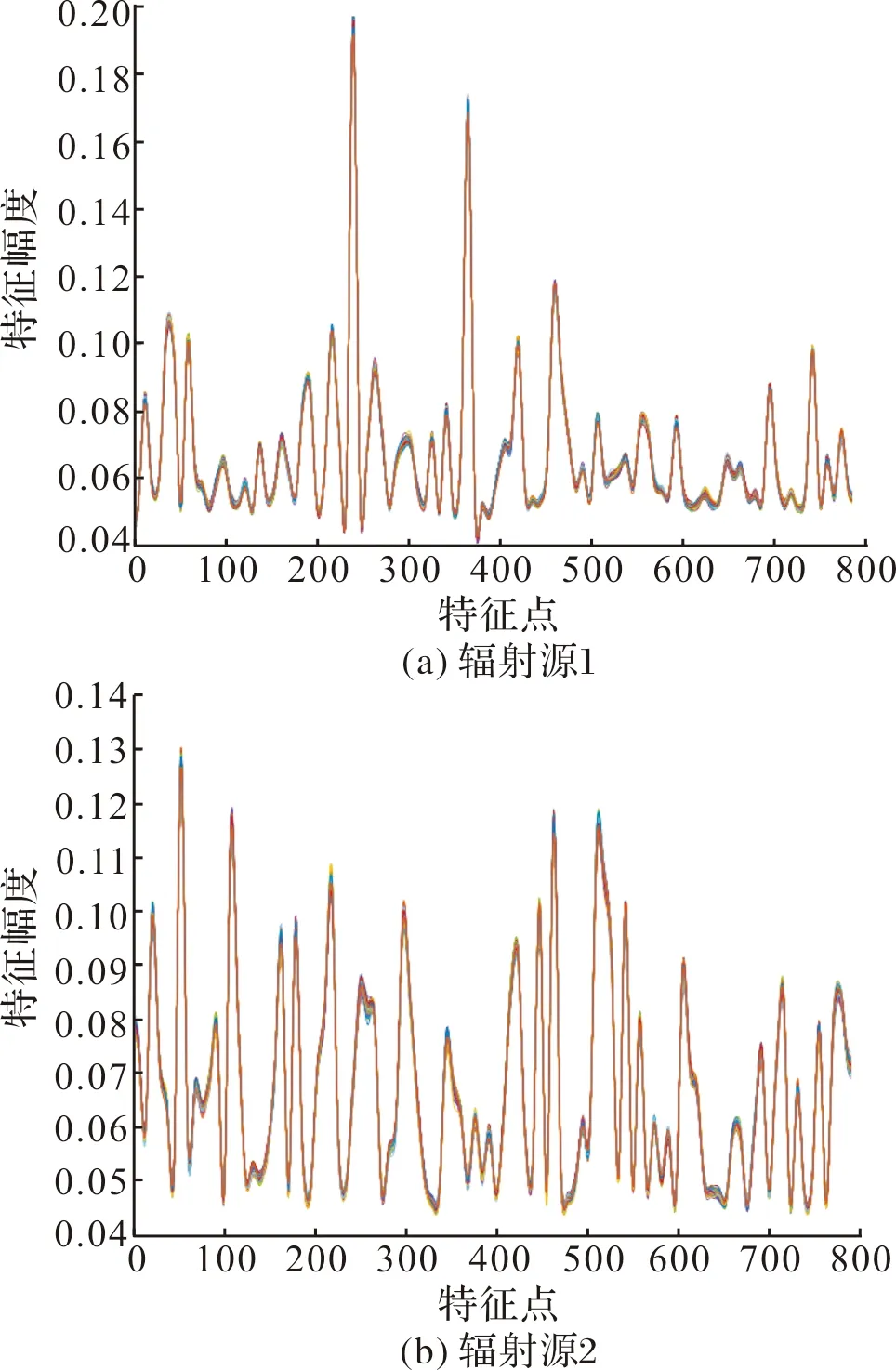
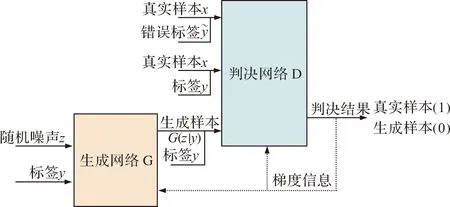
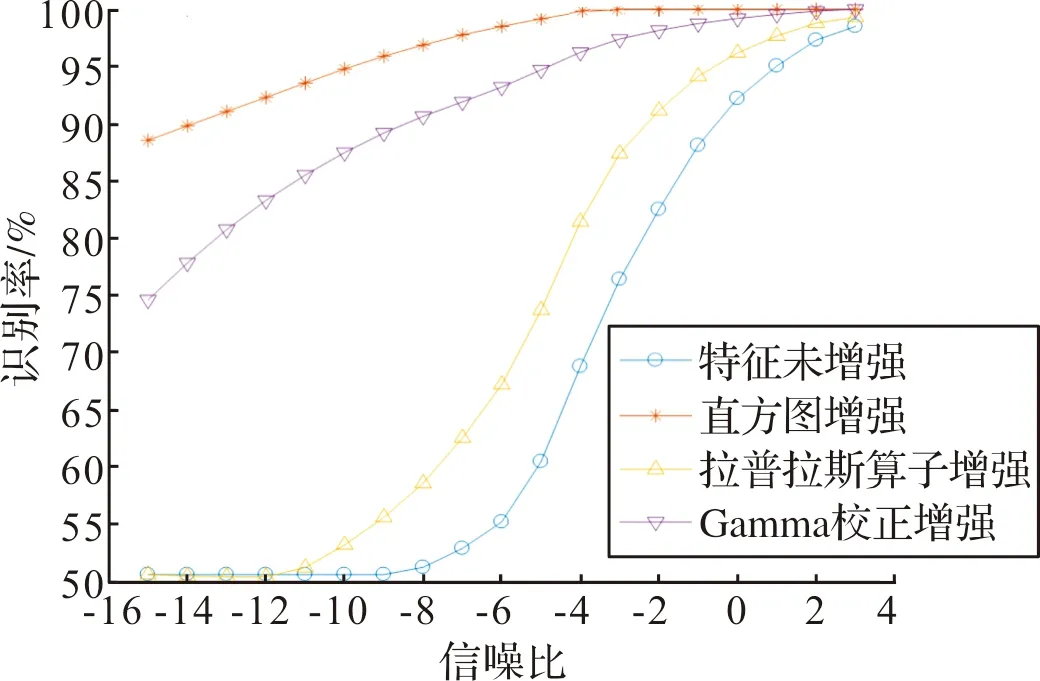
2)特征提取。将灰度矩阵V输入到SAE中进行特征提取，通过调节网络参数，使得网络输出维度为M×n的特征矩阵HM×n，此处n<

3)特征增强。通过直方图修正法、灰度变换法、图像滤波法等图像增强的方法将输出的特征矩阵H进行特征增强，最后输出得到增强特征矩阵KM×n。

4)样本扩充。将增强特征向量KM×n输入到SCGAN中进行训练，训练完毕后提取SCGAN中的生成网络模型Model_G，通过Model_G得到M1个生成特征样本，将生成特征样本与增强特征样本混合，得到新的增强特征矩阵K(M+M1)×n。

5)分类识别。将增强特征矩阵K(M+M1)×n输入到CNN中进行训练，最后通过SoftMax分类器进行识别，输出识别概率。

1.2 图像预处理

以线性调频(LFM)信号s(t)为例，对其加汉明窗进行STFT，得到S(t,f)，如图2所示。然后对时频图中有信号的部分进行截取，通过边缘检测技术提取时频图轮廓，然后找到时频图轮廓重心，以重心为中心点提取300×300的像素点，如图3所示。

图2 LFM信号时频图

图3 LFM信号截取后时频图

最后将图像转化为灰度图像，并进行下采样和向量化操作，得到长度为60×60的时频图灰度向量v。

1.3 SAE特征提取

对预处理后得到的时频图灰度向量v通过SAE进行特征提取，SAE网络的输入大小设置为3 600，第一层输出大小设置为196，第二层输出大小设置为100。

图4和图5给出了在2台辐射源各100个信号样本经过2层SAE特征提取后第一层和第二层的隐含层特征，发现100个信号样本第一层的隐含层特征基本重叠，说明特征稳定，而100个信号样本第二层的隐含层特征在幅度上存在一定的差异，说明第二层的特征存在一定的不稳定性，因此可以认为，辐射源个体信号时频图经过SAE特征提取后的第一层隐含层特征比第二层稳定。

图4 两台不同辐射源信号经过SAE特征提取后第一层隐含层特征

图5 两台不同辐射源信号经过SAE特征提取后第二层隐含层特征

1.4 特征增强

常用的图像增强算法主要有灰度变换增强[11](拉普拉斯算子锐化、Gamma校正等)和直方图增强[12]算法。以直方图增强算法为例：首先将信号SAE第一层的输出转化为图像形式，然后将这幅特征图像转化为灰度图，利用直方图变换技术对特征信息进行增强。

图6(a)是特征图的原始图像，可以看出整个特征图像素点之间的差异不是很明显，无法轻松辨别其细节特征。图6(b)给出了原始特征图像的256级直方图，可以看出，特征图像的灰度级主要集中在[0,30]之间，为了更好的增强特征图像信息，可以选取[0,30]的灰度级进行处理并均衡化。

图6 原始特征图像及其256级直方图

从图7可知，调整后的直方图在亮调细节方面比原始图像有了显著提高，动态范围明显增加。经过均衡化后图像质量得到进一步改善，特征图像亮度分布均匀，阶调变得更加柔和，直方图由原来的亮调集中变为分布基本均衡，达到了特征增强的目的。

图7 均衡化30级灰度图及其直方图

1.5 SCGAN生成特征

SCGAN在条件生成对抗网络(CGAN)的基础上改变了条件信息y，并在判决网络的损失函数中添加混叠惩戒项，将错误标签与真实样本相结合输入到判决网络。SCGAN的基本结构如图8所示，条件信息y定义为辐射源个体的标签值。

图8 增强条件生成对抗网络模型

GAN网络中的生成网络和判决网络均采用3层全连接层，将100维噪声与1维标签连接成101维数据输入到生成网络中，通过3层全连接层和3层BN层后将维度转为784维生成样本，再将784维生成样本与真实标签结合成785维数据输入到对抗网络中，同时将真实样本与真实标签结合成785维数据输入到对抗网络中，此外对抗网络还将输入错误标签与真实样本的结合数据。生成网络与判决网络中第一层和第二层的激活函数均为LeakyReLU函数，最后一层的激活函数采用Sigmoid函数，其中加入Dropout层和BN层防止模型过拟合。

实验中的生成网络与判决网络中的优化器均采用Adam优化器，其学习率设置为0.002，动量为0.5，每个批次32个样本，每一批样本在生成网络和对抗网络中交替训练各一次，训练批次设置为2 000，损失函数均为交叉熵。

2 实验结果与分析

通过3台同厂家同型号的软件无线电外设(software defined radio,SDR)USRP N210进行实测信号的采集和接收。将其中2台N210作为发射机，先后发射相同的信号，另1台作为接收机，发射位置和接收位置保持一致。在实验室环境下，发射机和接收机的距离为1 m，此时可以忽略信道噪声带来的影响。两台发射机均发射正弦脉冲信号，载波频率设为0.8 MHz，采样频率设为10 MHz。将接收到一段时间内的脉冲信号进行截取，通过MATLAB程序对脉冲进行检测并截取，截取长度为250(其中脉冲部分长度为150，噪声部分长度为100)。

2.1 特征增强性能分析

忽略小样本条件，将特征增强前后的特征直接输入到CNN中进行识别。卷积神经网络的训练轮次设置为10，批大小设置为64，损失函数选择为交叉熵函数，学习率为0.01。CNN中输入总样本数为6 000，每台辐射源各2 000组样本，将其打乱后进行训练和测试，其中训练集占总样本的70%，测试集占30%。每个信噪比下各进行500次蒙特卡洛实验。为了比较不同特征增强算法的性能，同时考虑了3种特征增强方法：直方图均衡化、拉普拉斯算子锐化以及Gamma校正。最后得到识别率如图9所示。

图9 特征增强前和增强后的真实信号识别率

图9给出了不同信噪比下的识别率曲线，其中采用特征增强方法的识别性能比未采用特征增强方法有明显提高。如未采用特征增强时，CNN在-9 dB时已经无法识别出辐射源个体，而经过特征增强后，CNN的识别性能均有所提高。3种特征增强方法中，直方图增强法的识别性能最优，平均提高9 dB；其次是Gamma校正增强方法，平均提高7 dB；最后是拉普拉斯算子增强方法，识别性能平均提高3 dB。

2.2 小样本下算法性能分析

针对不同算法，分别在不同信噪比下进行实验。每台辐射源的样本个数设置为400，将2台辐射源的各2 000个真实样本作为测试数据。算法一将每台辐射源信号样本进行数据预处理得到时频灰度矩阵，对时频灰度矩阵直接进行SAE特征提取以及直方图均衡化后输入到CNN网络中进行识别。算法二将每台辐射源信号样本进行数据预处理得到时频灰度矩阵，通过SCGAN生成每台辐射源各1 600个样本，将生成样本与原始样本融合得到每台辐射源各2 000数量的时频灰度矩阵，对时频灰度矩阵进行SAE特征提取以及直方图均衡化后输入到CNN网络中进行识别。算法三将每台辐射源信号样本进行数据预处理得到时频灰度矩阵，对时频灰度矩阵进行SAE特征提取以及直方图均衡化，然后通过SCGAN生成每台辐射源各1 600个样本，将生成样本与原始样本融合得到每台辐射源各2 000数量的增强特征矩阵，输入到CNN网络中进行识别。最后得到识别率如图10所示。

图10 不同信噪比下的识别率

图10给出了3种算法在不同信噪比下的识别率曲线，可以看到，通过SCGAN扩充特征样本可以大大提高算法的识别性能，说明SCGAN可以很好地拟合增强后的特征分布，从而有效扩充样本，提高识别性能。但是通过SCGAN扩充时频灰度向量却对提高识别性能没有帮助，说明SCGAN在扩充时频灰度向量时，很难对其进行较好的拟合，原因是由于真实信号生成的时频图数据维度过高。此外，在相同识别率条件下，算法三识别性能较算法一和算法二均提高了15 dB，说明了文中算法的有效性。

针对小样本实验中的算法一和三，分别在不同训练样本数下进行实验。样本的信噪比设置为-3 dB，每台辐射源的样本数范围设置为50～300，间隔设置为50，每台辐射源的真实训练样本数目设置为400，每台辐射源的生成特征样本个数为2 000个。采用不包含训练样本的每台辐射源各1 000个真实样本进行测试。

图11给出了不同训练样本数下，算法在加入SCGAN前后的识别率变化情况。当识别率同时达到98%时，采用文中算法仅需每台辐射源各100的训练样本，而未加入GAN的算法需要每台辐射源各400的训练样本，在达到同样识别率情况下，需要的样本数量仅为改进前算法的25%。

图11 不同训练样本数下的识别率

3 总结

提出了一种基于小样本条件的雷达辐射源个体识别算法，算法首先提取雷达脉冲信号的时频图，然后将得到的灰度图进行SAE特征提取，利用图像增强算法处理实现特征增强，然后输入到GAN中进行样本扩充，最后输入到CNN网络中进行识别。实验结果表明：采用特征增强方法的识别性能比未采用特征增强方法有明显提高，识别性能的改进程度高低依次为直方图增强法、Gamma校正增强法和拉普拉斯算子增强法；加入SCGAN后大大提高了算法在小样本条件下的识别性能，在相同识别率下，算法识别性能平均提高15 dB，所需训练样本数量与改进前相比减少了75%。