分布式协同航弹圆弧路径规划及非线性制导律设计

米长伟，吴 旭，纪辞禹，夏云凡

(兵器工业集团航空弹药研究院，哈尔滨 150036)

0 引言

协同攻击武器是基于“集群”作战思想，以空间分布的低成本单一功能载荷集中建立功能优势。协同攻击的集群作战形式是未来空战的一个关键领域，国内外学者对其进行研究，并取得了一些研究成果[1-3]。

BTT导弹可用于分布式协同作战，且BTT控制技术具有高机动性、高气动稳定性等众多优点，其自动驾驶仪基于极坐标操纵体制，在实现对目标的跟踪过程中，能快速操纵弹体旋转，将导弹的主升力面对准目标航路点，最大限度利用主升力面所能提供的法向过载，提高导弹的机动能力[4]。

针对BTT控制技术，国内外学者在航迹跟踪和制导律优化方面均取得了一些研究成果。崔生旺，黄叙磊等针对BTT导弹引入无人机的大圆航线飞行技术，设计了非线性制导律，但并未涉及滚转通道抖动问题的处理[4-5]。冒云慧等针对无人机航迹跟踪问题，提出了具备抗风能力的横向非线性制导算法，该算法需要确定合适的距离参数，在实际应用中受到一定限制[6]。贾鹤鸣等实现了UUV的航迹跟踪控制，设计了非线性迭代滑模跟踪控制器，并结合Lyapunov稳定性理论，分析了控制器的稳定性[7]。Manyam,Mejias,黄得刚等针对无人机无动力进场阶段的制导进行了研究，并进行了仿真分析和试验验证[8-10]。

在分布式协同BTT航弹的研制过程中，航向机动时受协调支路影响，滚转会产生抖动。因此，在分析相关研究成果的基础上，提出了适用于集群协同BTT航弹的双椭圆航路越界及过点判断策略、圆弧路径规划和与之适应的非线性制导律优化算法，并利用Lyapunov稳定性理论分析了该算法的稳定性。

1 航弹航路规划及制导律设计

航弹任务航路由若干航路点构成，简化的直线航路规划如图1所示。

图1 直线航路规划几何示意图

在制导控制中，由航迹建立发射坐标系下的XRP2ZR平面内，P0P1为规划的直线航路；因存在导航和控制偏差，实际飞行航迹为P0P′1，且P′1点在发射系中满足z1=0的条件。

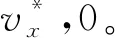
首先，得到非滚转弹体坐标系下的法向过载和侧向过载，其表达式为：

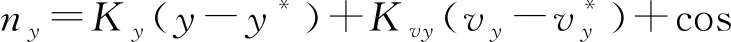
(1)

(2)

式中：ny指向y轴方向;nz指向z轴方向;Ky，Kvy为法向过载系数;Kz，Kvz为侧向过载系数;ϑ为俯仰角。

然后，通过这两个过载求得体系下的过载指令:

(3)

(4)

γctrl=0

(5)

式中：ny_bdy为俯仰通道制导指令；nz_bdy为偏航通道制导指令；γctrl为滚转通道指令。

直线航路规划时，式(2)可简化为:

nz=Kzz+Kvzvz

(6)

2 分布式协同BTT航弹圆弧路径规划及非线性制导律优化

在集群协同BTT航弹间，为解决航弹防碰撞问题，需要严格设计安全航路。针对这一问题，拟从两个方面入手：第一，设计协同航弹的双椭圆安全区域；第二，单枚航弹的航迹跟踪。

建立以目标点为原点O的目标发射坐标系，OX轴在目标点水平面内由发射点指向目标点方向，OY轴沿目标点的铅垂线向上。

2.1 协同航弹间双椭圆航路安全边界

如图2所示，根据3个航路点及安全边界参数b，构建安全边界椭圆Ellip1和Ellip2，椭圆相交区域为阴影区域Dz。

图2 双椭圆安全边界几何示意图

由航路点P1，P2和P3的位置坐标，可计算出航路点P1，P2之间的距离dp1。同时计算得到安全边界解算阈值Lthd为：

(7)

椭圆Ellip1和Ellip2分别以航路点P1，P2和P2，P3为焦点。根据椭圆焦点特性，可通过点到航路点的距离之和与Lthd的大小，判断点与椭圆的位置关系。

结合航路点P1，P2在笛卡尔坐标系下对应坐标值，可计算得到航弹距离航路点P1和P2的距离之和d1，与到点P2和P3的距离之和d2，进而确定安全边界越界标志Flag。当且仅当Flag为2时，判定航弹越过安全边界。定义Sgn为取变量正负号，则有

Flag=Sgn(Lthd-d1)+Sgn(Lthd-d2)

(8)

Flag融合安全边界越界判据和航路点过点判据于一体，即Flag为0时，可以作为航路点的过点判据。

2.2 圆弧航迹规划

如图3所示，圆心O点坐标为(x0,y0,z0)，则有

图3 圆弧路径规划几何示意图

(x1-x0)2+(z1-z0)2=R2

(9)

(x2-x0)2+(z2-z0)2=R2

(10)

根据目标发射坐标系的特性，目标点的坐标为(0,0,0)，有

(11)

式(9)和式(10)展开，并整理得到:

(12)

(13)

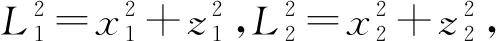
(14)

(15)

进而可得:

(16)

(17)

同时，根据(xc,yc,zc)的方程:

(xc-x0)2+(zc-z0)2=R2

(18)

可得:

(19)

进一步，对式(18)求导，可得

(20)

(21)

2.3 制导律设计优化

圆弧路径规划得到的圆弧航路点在发射系XRP2ZR平面内，其中ZR轴方向的实际位置分量为zc。集合航路为凸面体与XRP2ZR相交形成的图形，并且zc-z0仅选择正值，进而可得

(22)

同时，由圆弧路径规划特性约束可知，圆弧所对应的弦PP2为非直径，因此可剔除式(21)的奇异点，且vc的解算恒有解。

进而，可得修正侧向过载指令为:

nz=Kz(z-zc)+Kvz(vz-vc)

(23)

2.4 非线性优化制导律的稳定性证明

(24)

结合式(23)可得:

(25)

(26)

引理1：设A,E,F均为n阶实方阵，C∈Rm×n，且

1)A=EF；

2)FT+F=-CTC；

3)E>0；

4)(A,C)能观。

证明：由Lyapunov定理，结合条件4)可知，存在对称正定矩阵P满足下述Lyapunov方程:

ATP+PA=-CTC

(27)

根据条件3)，令P=E-1，并结合条件2)、 3)，可得:

ATP+PA=FT+F=-CTC

(28)

定理1：二阶阻尼式(25)系统方程渐进稳定的充分条件为:

M>0,DT+D>0,K>0

(29)

对于式(26)系统方程，有

(30)

由式(29)与式(30)可知E>0，且存在n阶可逆矩阵T，满足

DT+D=TTT

(31)

可令C=[T0]，则

FT+F=-CTC

(32)

进而，引理中的条件1)至条件3)均成立，针对条件4)，令

(33)

由于矩阵T可逆，则

(34)

再由M-1K可逆，得

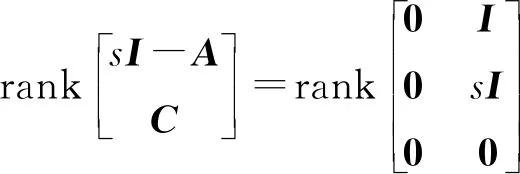
(35)

3 数学及半实物仿真

半实物仿真系统主要由仿真控制系统、弹载计算机、转台运动模拟系统等组成。其中，发动机采用数学模型，舵机采用实物，导航系统姿态数据由转台模拟，航弹飞行数据、航迹数据由数学模型得到。

主要系统参数为：IMU选择MEMS IMU，陀螺零偏为10°/h，加速度计零偏为1 mg，AHRS传感器精度约为0.5°,0.5°,2°，组合导航测速精度0.1 m/s，定位精度为水平10 m，高程15 m。

半实物仿真中设计的航路为：爬升-定高巡航-降落回收，其中定高巡航时先直线飞行，然后做半圆弧转弯，再转直线飞行。

如图4所示为飞行过程中姿态角的变化曲线，可以直观的看出偏航角完成180°变化。

图4 飞行过程中姿态角曲线

如图5～图7所示，为建立的地面发射系的X，Y，Z方向的位置曲线。在转弯时，完成航迹参考点的切换时，重建了发射系，因此在X方向上产生了跳变。

图5 转弯过程地面发射系的X向位置

图6 转弯过程地面发射系的Y向位置

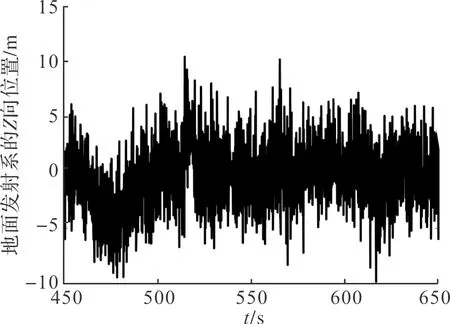
图7 转弯过程地面发射系的Z向位置

图8～图10为转弯时姿态角的对比曲线，可以看出传统制导律方法在俯仰、偏航和滚转3个方向均产生了抖震，其中滚转方向幅值最大，这种现象对飞行过程的能耗和平稳性均有不利。而文中提出的非线性制导律改进方法，有效抑制了抖震带来的震荡。其中，航向角实现了平滑，滚转角抖震幅值降低到2°左右，比改进前降低了一个数量级。

图8 转弯过程俯仰角对比曲线

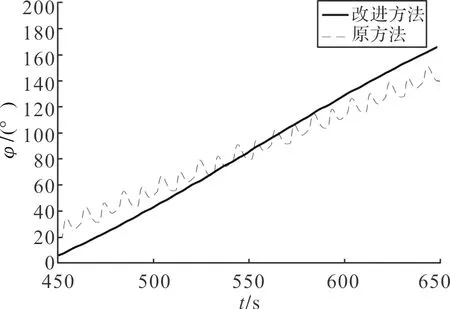
图9 转弯过程偏航角对比曲线

图10 转弯过程滚转角对比曲线

4 结论

通过对航弹航路优化及制导律进行分析，针对航路设计及追踪问题进行了双椭圆航路越界和过点判据的设计，实现了对航路点的遍历以及航路寻迹约束。针对试验中由偏航机动导致的滚转通道抖动问题，设计了圆弧路径规划及制导律优化算法，有效抑制了通道抖动，保证机动时姿态较为平稳。最后通过仿真试验，证明了提出的方法有效，能够为集群协同航弹研制工作提供技术支撑。