深部硐室长期稳定性的两个力学问题*

王明洋，徐天涵，邓树新，陈昊祥

（1. 中国人民解放军陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007；2. 南京理工大学机械工程学院，江苏 南京 210094；3. 北京建筑大学北京交通基础设施建设国际合作基地，北京 100044）

深部硐室围岩的长期强度与变形问题不仅是岩石力学的基本问题，也是当前我国诸如川藏铁路交通、水电水利、能源矿山和国防军事防御等重大工程，乃至地球物理及高能物理科学实验等基础设施深地下化建设中亟待弄清的问题。该问题的复杂性不仅在于深部非均匀裂隙岩体中存在高封闭应力且难以确定影响裂隙介质变形与强度的主要因素，还在于如何在岩体大变形及破坏情况下表征其固有属性。陈宗基院士早在20 世纪60 年代就已充分认识到岩体变形由岩块中的岩石介质变形和岩块边界面（结构面）附近区域以及岩体的弱化区（裂缝处）的变形组成，并基于流变学原理系统开展了岩体变形与强度特征的理论与实验研究；80 年代，他结合地球动力学、构造地质学和流变学方法，开创性地进行了岩体中封闭应力形成与释放、岩体随时间的强度变化与扩容、以及地下硐室围岩位移等现象的力学机理研究。强调了地应力（构造应力）在裂隙块状岩体运动以及不稳定渐进破裂中起着基本作用的观点。这些观点体现在有关岩石流变、回弹、松动、扩容以及长期强度等基本概念中，对认识地下硐室围岩长期稳定性与地质构造非协调变形和封闭应力相互作用的力学机理以及相关防控措施至关重要[1-5]。

在长期的地质活动作用下，深部岩体内部存在大量的断层、节理、裂隙等缺陷，它们将岩体分割成大小、形状不一的块体。岩体中裂缝的宽度可从构造断裂的百米级到微裂纹与矿物晶粒缺陷的10−8m，裂缝的延展长度可从106m 到10−6m，即从宏观断裂尺度到细观和微观裂纹尺度[6]。地质力学与地球物理领域不断发展的实验研究验证了Sadovsky 院士及其学派提出的岩体等级构造观点的正确性[7-10]。Sadovsky 院士[7]认为实际岩体可表示为由遵从等级序列的构造单元组成的集合体（块体），这些块体由软弱区隔开。构造单元边界可以是张开（未填充）的断层，也可以是部分填充的裂缝等不连续构造。在任何情况下，任意构造等级的岩体介质都可以表示成体积为Vi（i=1,2,···,N，其中N为等级划分的最深层次）的块体的集合体，这些块体具有不同的物理力学性质。

利用岩体中的间断尺度来对介质构造单元进行等级排列。假设最大的构造块为0 级块体，则组成0 级块体的构造单元由0 级块体中最大的间断划分，并被称作1 级块体（i= 1），依此类推（见图1）。在这样的岩体介质中，每一个单元都可以被赋予等级i（i=1,2,···,N）。

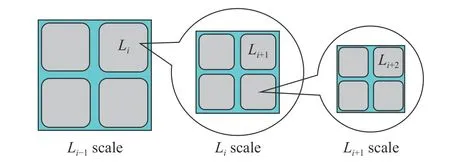
图1 岩体的构造等级示意图Fig. 1 Sketch of hierarchical structure of rock blocks

按此定义，含有i+1,i+2,···,N级构造块体的集合体组成了i级块体内部的独立构造块，而i级块体又是i− 1 级块体的从属单元。

上述岩体等级构造模型包括了所有等级的块体以及其中的软弱区域（不同等级块体之间的间隔），而且在每一个集合体中任意区域介质是非常不均匀的，这些区域包含了岩块，更高级块体的集合，或块体之间的间隙。

按照岩体构造等级这一学说，自然界中的岩体，大到大陆板块，小到细砂颗粒，甚至是晶体的结构单元，都具有嵌入特性或者层次重复性，在大的部分中嵌入小的部分，而后者又有更小的部分嵌入。然而，目前在研究岩体自然变形或诱发变形时，常把岩体看作为各向同性的连续体，因而岩体的应力应变状态以及力学过程广泛采用连续介质力学的数学模型描述（例如，弹性、塑性、蠕变、脆性和韧性断裂等概念）。其不足之处在于无法有效表征对应不同结构层次的空间及时间规模上岩体发生的变形及破坏过程，因此也就无法解释含能岩体的许多非线性力学现象[11-12]。这些非线性力学现象包括：

（1）在不同结构尺寸级别上发生着程度不同的块体运动。如Kocharyan 等[13]对地下核试验的场地效应调查发现，在距离爆炸较远处的地下硐室周围有“块体激活”现象，小型岩块（尺度为10−1～100m）的稳定可以通过工程措施来保证，而大型岩块（尺度为101～102m）的稳定无法通过工程措施实现。

（2）在工程级别的规模上发生着自然以及人为成因的微地震、岩爆等动力现象[14-15]。如在深地下进行大规模爆破时，距离爆源较远处的岩体即使经过几个小时甚至几天后也有可能出现岩爆、工程地震等灾害。显然这是由于扰动作用导致岩体约束解除，内部储存能量释放的结果[16]。

（3）硐室围岩破坏区在时间与空间上呈现渐进发展模式。锦屏一级电站主厂房洞周围岩的松动区随着开挖深入，从最初2 m 发展到最大17 m 以上，并且沿径向深度呈现间隔性分布[17-20]。白鹤滩电站右岸厂房岩体内部8.5 m 深度处，由于应力转移出现新生破裂，并且破裂面在一年多内不断扩展[21]。

（4）在实验室规模上发生由岩样内部能量释放引起的微细观裂纹的产生、发展与宏观破坏，以及扩容现象。如Revuzhenko[22]从深部岩体中取出的完整岩样，在静置一段时间后能自发快速崩解。若在完整岩样的表面刻痕或轻微敲击，则会加速其破坏过程。再如对深部岩样施加轴压后卸载，试样的高度与直径均会随着时间的推移而逐渐增大。显然这些现象中岩样破坏与扩容所做的功来源于内部储存的能量。

岩体固有的非均匀构造与封闭应力特性是产生上述现象最本质的原因。尤其对于赋存在高地应力有势场环境中的深部岩体，在掘进、爆炸以及地震等扰动作用下，随着不同尺度水平上应力场的不均匀性增加，该固有特性作用更加突出。虽然非均匀介质中多尺度、多阶段变形破坏的定量计算方法已取得长足进步，但由于岩体的实际构造特征有众多的初始条件，目前在计算上仍存在困难。如果将非均匀岩体的变形看成强烈非平衡系统，按照非均匀系统行为的统计物理规律，仅研究具有耗散的宏观结构单元变形行为，则问题可得到极大简化。

本文中利用Sadovsky 院士关于复杂地质岩体的等级构造学说，围绕深部岩体非均匀构造与封闭应力固有的统计力学属性，沿着陈宗基院士关于地下硐室长期稳定性力学问题方向，在作者相关研究基础上[23-25]，研究岩体固有的非均匀构造与封闭应力特性，以及初始地应力对硐室围岩长期稳定性影响的机制与破坏准则这两个问题。

1 岩体非均匀构造的固有力学问题

1.1 岩体非均匀构造的变形特征

岩体的变形特性是其最基本的性质，这些特性由两方面决定：一是由其组成部分（次级块体及其间隙）的变形及强度特征参数决定，二是由其整体的变形特征参数决定。根据外部作用大小不同，集合体构造单元的变形可以是协调的，也可以是不协调的。由此，集合体的状态在某一时刻可以是密合的，也可以是非密合的。如果在变形的初始阶段所有构造等级的构造单元处于密合状态（见图2（a）），那么，根据流变学的概念，可以划分出非均匀介质的三个变形阶段。

（1）可逆变形阶段（见图2（b））。该阶段构造单元的所有组成部分的变形均处于弹性极限内，介质仍保持其连续性。在外部加载解除后介质返回到初始状态。

（2）不可逆协调变形阶段（见图2（c））。在该阶段，塑性非协调变形区域形成，但是没有破坏介质的连续性，在较低强度构造单元上形成的塑性非协调性可由其他区段的弹性变形来补偿。这时产生的内部应力在外部荷载解除后仍然存在。

（3）非协调变形阶段（见图2（d））。当弹性变形不足以补偿塑性变形时，不可逆变形使构造单元失去连续性，该构造单元在一个或多个软弱面上发生断裂，进而产生旋转与平移。应当注意到，n级构造单元上非连续性的出现使其整体变形得以部分恢复，这导致在n−1 级构造单元（尺度更大的块体）中出现非协调性变形所需的应变更大，即出现时间滞后效应。

图2 第n 级非均匀构造单元的变形阶段Fig. 2 The deformation stages of the nth non-uniform structure

如上所述，随着外力作用的强度增加，微观水平上应力场的不均匀性不断增加。根据非均匀系统统计物理规律，必然形成与外力作用相应的耗散结构，并且耗散结构的线性尺寸L∗对应于岩体中的自然岩块尺度。如果外力作用引起的变形不超过临界值 ε∗，那么不可逆变形就不会发生。在块系介质中最大变形发生在软弱面附近，因此应变可按 ε =U0/L∗计算，其中U0为邻近块体面之间的相对位移。文献[26]中给出了 ε∗的计算方法，其中把现实的岩体看成是时变的非平稳系统，根据地构造运动中积累的众多资料得出 ε∗=(1 ∼2)×10−5。需要注意的是，破坏时的应变一般为10−4，这也就意味着岩体在产生不可逆变形之后，到发生破坏之前，仍能产生一定的应变。

1.2 岩体非均匀构造的封闭应力

式中：< >表示对体积V的平均。

式(9)表明，非均匀介质变形时产生的塑性协调变形，在外力卸载后将导致残余内应力的产生，其大小和状态（包括残留应力值）不仅由变形增降确定，也由所考察的构造集合体中单独区段的变形模量差值∆E i所确定，∆E i可以看作是介质具体区段的缺陷程度。

岩体的封闭应力特性对深部围岩的长期稳定有两个重要影响：

（1）岩块单元在外载彻底卸去后，单元内部可能出现局部的拉应力，造成单元的拉伸破坏，这一特性对深部围岩的变形破坏形态具有重要影响[28-29]；

（2）岩块单元在外载彻底卸去后很大一部分能量还保存下来，在爆破或地震等动力扰动作用下，这部分储存的能量可以释放，既能缓慢释放，也可快速释放，岩体的这一特性非常显著地影响着围岩动力的稳定性[30-32]。

2 深部硐室围岩的长期变形问题

深部硐室围岩长期稳定的防控技术，本质上是为了防止硐室邻近区围岩因蠕变或破碎而引起的坍塌作用。深部硐室开挖后围岩的向内收敛会在支护结构上产生数百甚至数千吨每平方米的压力，支护结构必须在没有断裂的情况下承受位移，显然，“刚性”支护会因难以承受这些位移而断裂。因此，深部硐室围岩长期变形（长期变形状态下的位移）的定量评估是长期稳定支护体系设计的基础。

研究静水压力状态下大深度圆形水平硐室围岩的变形破坏问题时，硐室可简化为轴对称问题，选用柱坐标系（r，θ，z），即取主应力σr沿径向坐标、σθ沿切向坐标、σz沿轴向坐标。在工作面掘进过程中，工作面附近的径向应力σr减小到零，切向应力σθ的变化取决于介质变形性质（见图3，应力状态随时间而变化）。对于长坑道，一般认为σz的变化不大，因此硐室的变形可看作是平面应变问题（ε0z=0）。在上述条件下，地下圆形硐室围岩最大剪切应力为τ=(σθ−σr)/2，当σ0≥τmax（其中σ0为初始地应力，τmax为岩石的剪切强度极限）时，由经典弹塑性理论可知硐室围岩出现塑性区，一般认为此时初始地应力对应的埋深即为硐室位于“深部”的临界深度。

图3 硐室开挖前后侧墙围岩应力状态的变化[1]Fig. 3 The change of stress state of surrounding rocks before and after the tunneling[1]

随着埋深进一步增加，硐室围岩状态逐渐向复杂围岩应力应变状态过渡。这种过渡与围岩产生的非弹性变形和破裂有关，在过渡中出现峰值后岩体的非线性特性，其中主应力之间的比例和主方向都可能发生变化，此时对剪切强度的评估非常重要。因此，研究硐室周围的应力应变状态就意味着研究岩体的剪切强度。

2.1 深部硐室围岩的剪切强度与破坏准则

2.1.1 Coulomb-Mohr 强度准则

可以借助摩尔圆来讨论硐室围岩的强度，如图4所示。摩尔圆的包络关系可以由下式表达：

在开始使用在线社交应用时，用户需要先向在线社交应用提交自己的隐私需求，即，对不同类型的请求者，他们最后看到的隐私信息的详细程度。这些不同的需求以隐私规则的方式存储在数据库中，由在线社交应用进行管理。用户只要定义好自己的隐私需求，在以后的使用过程中系统会将他的需求应用到他所有发布的消息中，不需要用户自身来管理各种权限的请求者可以得到什么样的内容，简化了用户的工作。

图4 硐室开挖前后侧墙围岩应力圆[1]Fig.4 The stress circles of surround rocks before and after the tunneling

式中：σn=(σr+σθ)/2。

众所周知，式(10)所示的强度准则由内摩擦角和内聚力两个特征强度参数来近似描述，它反映了围岩加载直至断裂的力学行为，但只涉及第一、三主应力，这意味着在构建摩尔圆包络关系时不考虑最大摩尔圆之外的其他摩尔圆。目前有众多的表达式来表示τ 与σn之间的关系[33]，但是有两个问题需要强调：第一个问题是，在这些关系式中σz不影响强度的von Karman 关系：即在最大摩尔圆达到极限时，不会破坏第二主方向上应力与应变的弹性关系；第二个问题是，这些关系式表达的脆性破坏强度准则不依赖于σz，材料弹性地达到断裂点[34-35]，很多岩石的变形和强度数学模型都是如此。

2.1.2三维强度准则

在复杂应力条件下，仅考虑第一主应力σθ与第三主应力σr所得到的岩石强度与实际有较大偏差，为此Shemyakin[36-37]通过引入Lode 参数µσ来研究第二主应力σz对强度的影响，他提出的三维强度准则为：

式中：τ1=(σz−σr)/2，τ2=(σθ−σz)/2。

式(11)所表示的是一个强度曲面，当µσ取不同值时即为不同应力状态下的强度曲线（见图5）。其中µσ影响的力学意义在于：在复杂应力状态下（µσ≠0），材料的强度不仅由最大剪切力决定，同时也由τ1和τ2决定，即不同类型压力状态导致不同的变形过程。

图5 三向应力状态时的强度准则Fig.5 Strength criterion at triaxial stress state

为了得到式(11)的函数曲面，必须进行三轴加载实验。图6为根据式(11)对文献[20]中锦屏大理岩真三轴实验数据进行整理的结果，岩石试样取自深约2.4 km 的锦屏二期地下实验室。图6（a）显示，随着 µσ的增大，不同围压时大理岩强度均有不同程度的增大。通过设定不同的应力状态（µσ）进行真三轴加载实验，可获得一系列强度包络线族，如图6（b）所示，进而得到式(11)所表示的强度空间曲面。

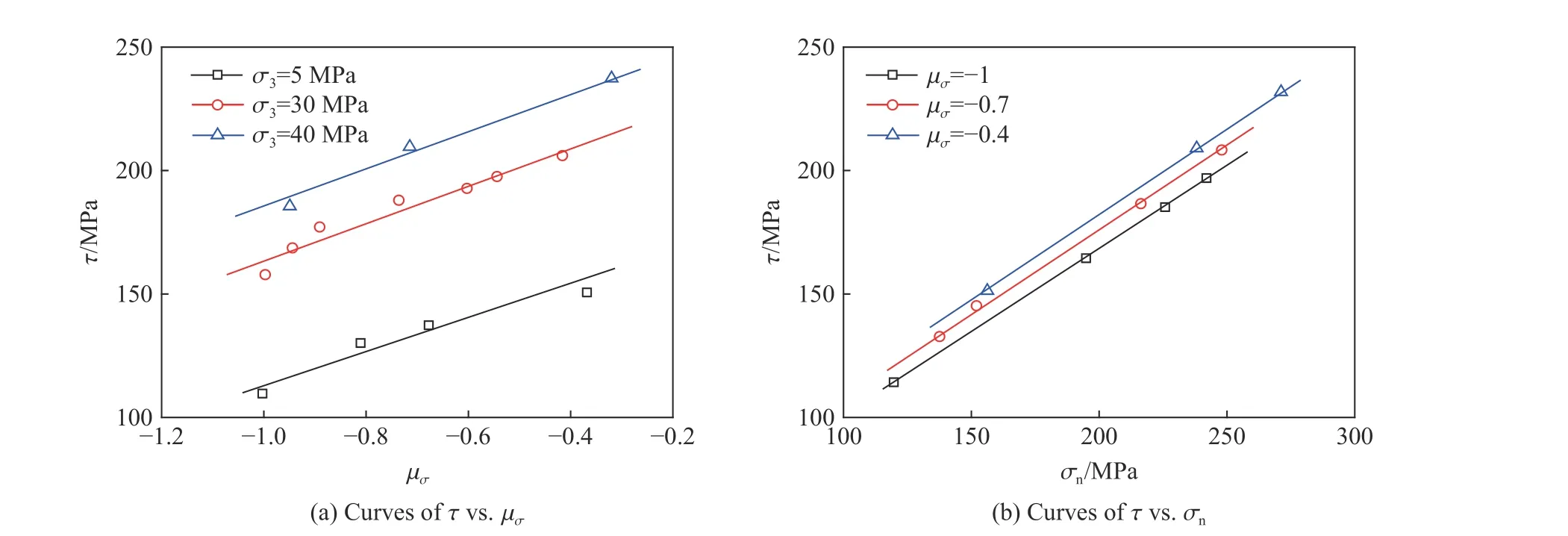
图6 锦屏大理岩真三轴实验结果Fig.6 The true triaxial test results of themarble in Jinping.

2.1.3深部围岩峰后长期变形特性

如上所述，深部硐室围岩的强度不仅由最大剪切力决定，同时也由τ1和τ2决定。即在复杂应力状态下（µσ≠0），Lode参数 µσ不仅在评估原始应力状态时应当考虑，在深部硐室工作面掘进的方向上也应当考虑。

在评价深部硐室长期稳定性中，也必须考虑切向力τ、τ1和τ2在直至破裂点的变形过程中的作用，如图7中应力应变曲线τ=τ(γ)所展示的那样，围岩在剪切应变为γe时达到剪切强度，而直至为γ0时才发生宏观破碎，图中γ=εr−εθ为主剪应变，εV=εr+εθ为体积应变。因此用应力达到极限应力状态来判断围岩达到强度极限或认为围岩丧失承载能力是不充分的，必须考虑围岩峰后的变形特性，包括不可逆剪切变形、体积扩容（剪切或拉伸），以及在不可逆变形区域的裂缝极限宽度。

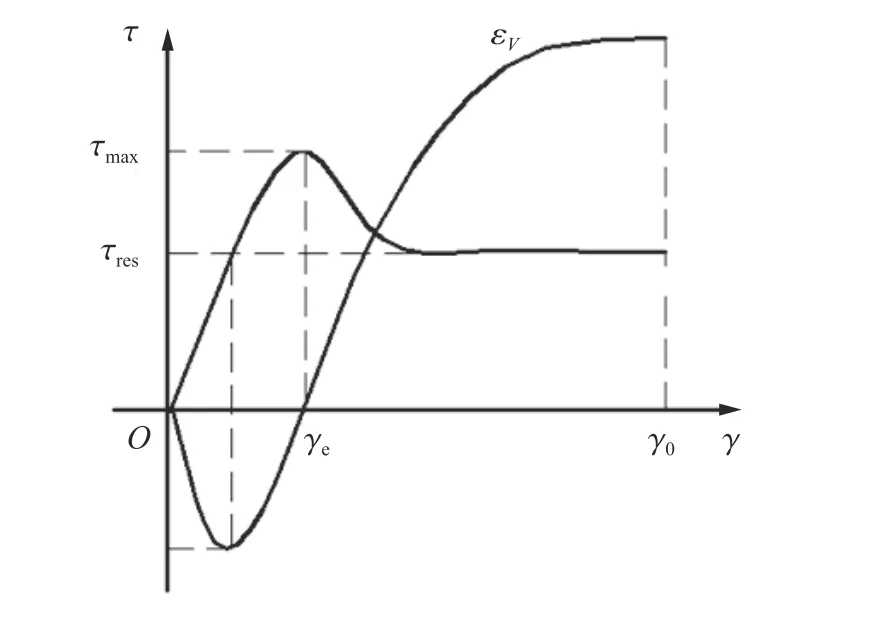
图7 体积变形与剪切变形的关系Fig.7 The relationship between bulk and shear deformations

深部硐室围岩的峰后变形行为均伴随着块体间的互相转动与滑动等各向异性特点，滑移面上的法向应力（以及由此产生的摩擦力）和变形的时间效应（岩石中的蠕变和松弛）决定着不可逆变形与破坏的形态（剪切、劈裂）。体积的改变则与膨胀及破坏所形成的块体的大小有关，这种体积变化的效应正是深部硐室围岩稳定性控制最本质的问题。

2.2 深部硐室围岩长期变形机理

2.2.1地下硐室长期变形计算的一般公式

在研究围岩的变形与破坏（剪胀与劈裂扩容）过程中，可利用质量守恒定律计算硐室围岩不可逆变形区（塑性区）内介质的位移[38]。

图8为塑性区的位移示意图，ur为半径r处岩体的位移，uc为不可逆变形区边界处的位移，从半径r至塑性区边界c处的岩体在发生位移前后质量不变，取轴向长度为单位长度，则有：

图8 塑性区围岩位移示意图Fig.8 The deformation of surrounding rocks in the plastic zone

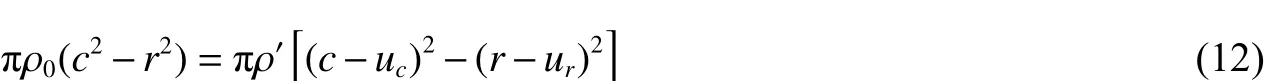
式中：ρ0与ρ′分别为位移前后岩体的密度。根据式(12)可进一步求得塑性区内半径为r处岩体的位移：

弹塑性边界的位移uc可由r=c处的连续条件得到[36]：

式中：ξ∗根据围岩分区边界条件而定，对于围岩弹塑性边界，ξ∗=γe(1−ν)，ν为介质的泊松比，γe为围岩的弹性极限剪应变，ξ∗为无物理意义的记号。考虑到ρ0/ρ′=1+∆V/V0=1+εV，εV为体积扩容应变（包括剪切变形导致的扩容以及劈裂带来的扩容），将其代入式(13)可得塑性区位移为：

半径为a的硐室边壁上的位移为：

上述依据质量守恒得到的表达式(17)对围岩的变形计算来讲可看作是一般形式。式(17)清楚地表明，围岩总的位移由第一项剪切变形和第二项扩容变形构成。

2.2.2深部硐室围岩长期变形机理

塑性区围岩变形由剪切变形和扩容变形构成，它们形成位移的机理不同，在总位移中所占比重也不同。对于剪切变形，选用Tresca 屈服准则，由经典弹塑性理论可知：当σ0≥τmax时，硐室围岩进入到塑性状态。要确定围岩的剪切变形破坏条件，如前所述（见图7），需引入τ=τ(γ)峰后变形曲线有关的参量。对于理想脆性材料，剪应力峰值对应的剪切应变为γe=γ0，其中γ0为破坏极限剪应变；但对于允许不可逆变形的岩石而言，γ0可超过γe一个数量级以上。该模型反映了真实岩体的重要性质，即存在岩体不可逆变形的临界应变γe以及岩体破碎的应变γ0。围岩在进入塑性状态以后将继续承载，同时产生较大的剪切变形。当围岩内壁应变达到γ0时，出现破碎。围岩因剪切破坏可能会导致单元体积变化，即剪胀效应。为了评估剪切导致的体积变化，按照上述模型选取最大的剪切变形值γ0，则体积变化 εV与破坏应变γ0的关系可以近似取为线性关系[39]：

式中：Λ为扩容系数，0≤Λ≤1，可用特殊实验设备测得扩容体积的变化。由于剪切破坏应变γ0是个常量，因而产生的体积变化一般不大。

深部硐室围岩体积变化的第二个原因是围岩可能发生“劈裂扩容”，即出现有平行于最大压应力的裂缝区或者是被裂缝区分离开的柱状构造[40-41]（见图9）。在各向不均匀压缩条件下，材料可能被破坏面分割（劈裂），其方向沿着最大压应力的方向。在本文所研究的问题中，最大压应力就是围岩中的环向应力σθ。在压应力 σθ作用下，即使另外两个方向存在压缩（约束）应力 σr和 σz，沿着σr方向也会形成拉伸变形，这些变形可以达到裂缝极限宽度（见图10）。

图9 地下硐室围岩劈裂示意图[1]Fig.9 The schematic diagram of spalling of rocks surrounding deep level tunnels[1]

图10 深部围岩劈裂示意图Fig.10 The splitting of deep surrounding rocks

当出现劈裂区时，围岩产生的位移可分解成两部分：一部分是直接在硐室附近区域中由岩体剪切变形产生的位移；第二部分是在围岩深处支撑压力区出现“虚假”隧道轮廓面而产生的位移（此部分位移主要来源于劈裂区围岩的体积扩容），如图11所示。这类“虚假”隧道轮廓面区域可能有几个，它取决于隧道所处位置的岩石压力和峰后变形状态下材料的剩余强度。需要指出的是，上述两部分位移均包含于质量守恒方程中，如式(17)所示。后面将给出上述两部位移的具体计算过程。

图11 深部围岩分区破裂示意图Fig.11 Diagram of zonal disintegration of deep surrounding rocks

深部硐室围岩分区破裂的发生条件仍是个悬而未决的问题，关于其在围岩什么位置发生需要回答两个问题：

第一个问题是在多大临界初始地应力下可能出现劈裂破坏？

第二个问题是大于临界初始地应力条件下，分区破裂的空间构造如何？

2.2.3深部硐室围岩劈裂破坏机制与条件

假设卸荷后应力调整的时间为tmax，根据经典弹性理论可知弹塑性边界处环向应力σθ的变化量为+τmax，径向应力σr的变化量为−τmax，轴向应力不变。假定应力变化过程为线性过程，那么应力转移过程中t时刻的应力（应力以压为正）为：

按平面应变计算，应用广义胡克定律可得应变为：

式中：Ee为岩石杨氏模量（卸载模量）。

缺陷处应力集中的演化方程为Maxwell 形式[29]：

式中：Ec为缺陷附近的压缩模量，为方便表征和测量可近似为岩石的塑性加载模量，∆ σr为裂隙附近σr方向的附加应力，J为特定尺寸缺陷上的应力集中系数，l为缺陷尺寸，η为附加应力的松弛速率，er为偏应变，er=εr−(εr+εθ+εz)/3，由式(21)可得：

将式(23)对t求导，并将导数代入式(22)可得：

根据初始条件t=0时∆σr=0，解式(24)关于∆ σr的微分方程可得：

一般情况下，η的量级为10−8m/s，同时围岩在开挖后因弹性回弹诱发松动而存在较大尺寸的缺陷，因此满足l＞＞ ηt，因而式(25)可以进一步简化为：

式(26)表明在径向方向存在拉伸的附加应力。这就回答了有关封闭应力重要特点的第一个问题，即围岩在卸载后可能出现拉应力。

将式(26)代入式(19)可得单元体内径向局部应力为：

式(28)回答了在多大临界初始地应力下可能出现劈裂破坏的问题。一般各向异性岩石的杨氏模量Ee大于加载模量Ec，因此根据式(26)求得的附加应力大小要大于各向同性(Ee=Ec)情况下的附加应力，即不均匀各向异性岩石较之均匀各向同性岩石更容易发生劈裂破坏。

Shemyakin[37]基于弹塑性理论给出了深部硐室围岩剪切破坏峰后的破碎条件。这就是为什么进入深部的硐室围岩一般更容易出现劈裂破坏或分区破裂现象的原因，该问题在实际深部工程中研究得还很少，需给予重视。

文献[25]初步回答了第二个问题（分区破裂的空间构造），给出的分区破裂半径为：

式中：ci为第i破裂区半径，i=1,2,3,···代表出现分区破裂的圈数。从能量释放的角度一般不会超过4圈（不包括硐室边壁出现小的劈裂区）。

引入围岩无量纲能量因子：

式中：Wp为开挖后围岩塑性区内应力释放的能量，M为塑性区岩体质量，cP为岩体纵波波速。k作为无量纲参数可以表征岩体的能量状态。

依据式(32)得到分区破裂半径ci/a与能量因子k之间的关系[25]（见图12和表1），可见随塑性区发展能量因子具有稳定的等级递减规律，直至塑性区围岩能量因子为1.4×10−9。

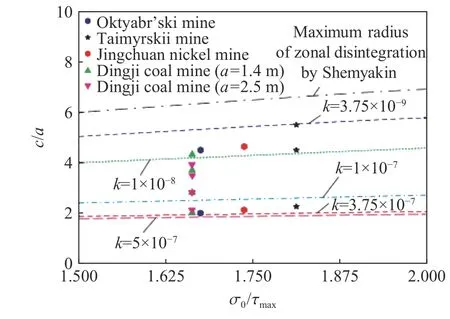
图12 分区破裂半径计算与监测结果对比[25]Fig.12 A comparison between the in-situ and theoretical radiiof zonal disintegration[25]

表1 分区破裂区半径ci/a 与能量因子k 之间的关系[25]Table 1 The relationship between the radii of zonal disintegration ci/a and theenergy factor k[25]

2.3 深部硐室围岩劈裂破坏不可逆位移

根据深部硐室围岩大量现场破坏现象，如图9（A 或B）所示，可以认为硐室附近出现劈裂破坏是由垂直或平行裂缝群构成。设每个裂缝宽度为δ，其占有的邻近岩块尺度为L，变形主要由裂隙开裂宽度构成，如果引入岩体等级构造的关系式δ=ψ∆L[9],其中岩石力学不变量为ψ∆=(0.5 ∼2)×10−2，那么硐室围岩的扩容体积变形为：

劈裂扩容与剪切滑移在边壁产生的位移依据式(17)可得:

将式(32)代入式(35)可得:

根据式(36)可以估算深部硐室在没有支护或支护能力不足的情况下，经过长时间围岩出现破裂的变形值。采用文献[17-18,43]提供的锦屏一级水电站地下厂房的基本参数与多点检测数据进行比较。

基本参数为：主变室跨度19.3 m，高32.7 m，等效圆形半径14.17 m；主厂房跨度25.9 m，高68.8 m，等效圆形半径为23.82 m；两个尾调室侧壁为竖直圆柱状，最大位移发生在半径较小的2号尾调室，半径为17.5 m。初始应力σ0=20～35.7 MPa，围岩为大理石，其基本参数为：τmax=15.5 MPa ，γe=1.275×10−3，ν=0.25，ξ∗=γe(1−ν)=0.96×10−3。

（1）现场监测数据：现场初始地应力与剪切强度比为σ0/τmax=1.3 ∼2.3，满足式(28)劈裂条件。主变室出现第一圈破裂区距边壁为8～9 m，且在深8 m 范围内围岩发生了劈裂，边壁局部变形达23.3 cm；主厂房第一圈破裂区距边壁13 cm，边壁位移最大为上游侧22 cm，下游侧24.7 cm；尾调室围岩未发生明显的劈裂破坏，边壁局部位移最大达12.5 cm。

（2）劈裂发生位置理论与实测对比验算：主变室第一圈破裂区半径与等效开挖半径之比c/a=1.64，与式(32)理论预测的第一圈exp(1/2)≈1.65相当吻合。主厂房c/a=1.55，与式(32)理论预测的第一圈exp(1/2)≈1.65基本吻合。误差主要来源于等效半径，主厂房高垮比为2.67，而主变室仅为1.7。

（3）侧壁位移理论与实测对比验算：侧壁局部位移变化是随时间而积累的过程，可以通过对ψ∆在其范围内取不同的值加以表征。根据式(36)分别得到劈裂扩容与剪切变形值，计算结果列入表2，可见实测的数值均在理论最大变形之内。其中尾调室尚未发生明显的分区破裂，因此变形还在发展的初级阶段，也与实际相符。

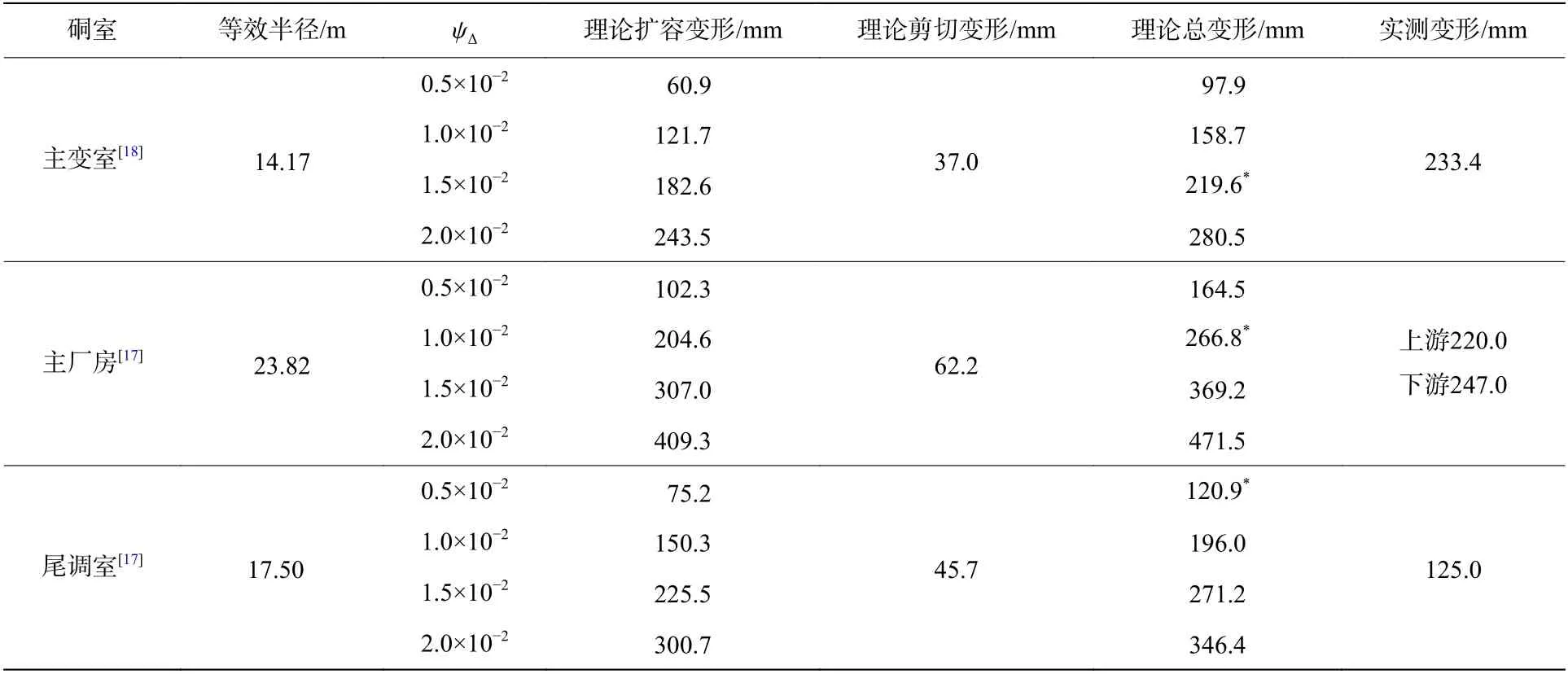
表2 围岩变形理论与现场实测结果对比Table 2 Comparison of the theoretical and in-situ results

根据式(36)计算的硐室围岩变形为开挖后无支护条件下的自然位移，而支护的存在会减缓变形的发展，因此实际位移都尚未达到模型预测的最终值。从表中也可以看出，围岩的变形主要为劈裂扩容变形，剪切的贡献较小，相差可达一个数量级。

根据深部硐室围岩的分区破裂范围，就可以确定锚杆长度，以满足围岩长期稳定而不开裂的条件；而根据围岩的变形量可以确定锚杆的强度，使其受力在正常工作区间内而不断裂。

3 结 论

（1）岩体固有的非均匀性与封闭应力特征，是决定深部硐室围岩长期变形与地震稳定性的最本质的因素。随着埋深增加，硐室围岩非均匀变形必将形成块系构造单元非协调变形，而围岩中封闭应力不仅影响其块系构造单元局部动力稳定性，也影响其长期变形破坏形态。

（2）深部硐室围岩的破坏准则不仅要考虑岩体三维强度准则，也要考虑围岩峰后变形及断裂准则。

（3）深部硐室围岩长期变形计算服从质量守恒定律，深部围岩出现劈裂的条件表明，围岩长期变形过程中更容易出现劈裂破坏导致的分区破裂化扩容效应，这种扩容变形比剪切不可逆变形高一个数量级。

（4）根据深部硐室围岩的分区破裂范围，可以确定锚杆长度，以满足长期稳定而不开裂的条件；根据围岩最大变形量，可以确定锚杆的强度，使其受力在正常工作区间内而不断裂。对于支护的变形位移计算理论将在后续研究中完成。

感谢梁文灏院士、冯夏庭院士提出的宝贵修改意见。