恒温法测爆热的快速系统辨识方法*

杨 杰，贺元吉，赵宏伟，徐明利，高洪泉

（中国人民解放军96901部队，北京 100094）

爆热是评价炸药作功能力的重要指标[1]，常用测量方法包括恒温法、绝热法与水下爆炸法[2-3]。绝热法和恒温法为直接且常用测量方法，两种方法均需获取测量结束时的内桶水温度（终点温度），区别在于，绝热法外桶温度需跟踪内桶温度、修正温升（爆炸产物向内桶系统传热引起内桶系统的温升）等于内桶温升，而恒温法外桶温度恒定、修正温升等于补偿后的内桶温升[4]；水下爆炸法为间接测量方法，需将冲击波能与气泡能折算至炸药爆热，误差较大[5]。

恒温法由于可测药量大（可达100 g）、测量精度高、硬件简单可靠，而成为测量炸药爆热的首选[1]。GJB 772A—97《炸药试验方法》中方法701.1中，恒温法的初期（外桶水升温结束至炸药起爆时间段）、末期（爆炸产物基本完成放热之后时间段）时间均为11 min，研究表明，如初期、主期（炸药起爆至爆炸产物基本完成放热时间段）、末期分别延长至21、80和21 min 时，测量误差将大幅减小[4]。

然而，恒温法测量时间比较长，如在主期或末期突遇异常温控、突然断电、软件崩溃等系统故障，会导致无法获取内桶水准确终点温度，此时常规测量方法宣告失败，造成很大的人力与物力的损失。因此，爆热的估算也是爆热测量的重要研究内容。俞统昌等[6]提出了混合炸药爆热的经验估算公式；韩早[7]提出了半经验公式法估算含铝炸药的爆热；此外，还有量子力学方法、神经网络方法、支持向量机方法等爆热估算方法[8-10]。可是，这些估算均为事前估算，目前尚未开展测量过程中爆热实时估算的研究。因此，本文中拟开展基于故障前内桶水温数据辨识炸药爆热的研究，提出爆热辨识算法，通过实验测试算法收敛性能，为爆热的实时估计提供理论依据。

1 量热计结构及恒温法测爆热经典算法

量热计（见图1）测爆热原理为：炸药起爆后，爆炸产物向内桶系统（由爆热弹金属壳、内桶水及其外壳组成）传热，根据内桶水的温升计算爆炸产物的放热量，再除以炸药质量即得到炸药的爆热。

根据GJB 772A—97中方法701.1，恒温法测量炸药爆热的经典计算公式为：

式中：TI(τ0)、TI(τn)、n分别为主期的初温（℃）、末温（℃）、温度读数个数；线性拟合初期、末期内桶水温升曲线得到的起点温度（℃）分别为θ0、θn，温升速率（℃/min）分别为V0、Vn；Δτ 为采样间隔(min)；Δθ、ΔtJ、Δt为补偿温度、经典方法修正温升、所有方法修正温升(℃)；C为量热计的系统热容（即内桶系统热容）(J/℃)；M1、M2为被测炸药、传爆药的质量，g；q为雷管爆热（J）；Q1、Q2分别为被测炸药、传爆药的爆热（J/g）。

2 爆热测量过程的传热分析

2.1 外桶系统向内桶系统的传热分析

由图1，内外桶之间的传热主要有热传导与热辐射两种方式，内外桶温差较小时（若要求辐射传热量线性计算相对误差不超过2%，外桶温度为25℃时，内外桶温差须不超过4℃），这两种方式的传热量均与内外桶温差为线性关系[11]：

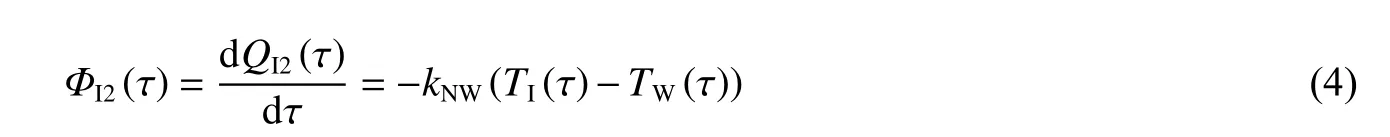
式中：ΦI2(τ)、QI2(τ)分别为外桶系统在时刻τ 向内桶系统传热的热流量、热量（为便于计算，QI2(τ)在初期、主末期阶段的计算起点分别为初期起始时刻τS、起爆时刻τM），TI(τ)、TW(τ)分别为内桶水、外桶水在时刻τ 的温度（对于恒温法，外桶水温度在初始调温、初期、主期、末期等阶段均为常量），kNW为综合内外桶热传导与热辐射的总导热系数。

在初始调温阶段，内桶水温须高于外桶水温（内外桶水温差记为TC）才能将搅拌产生的热量传导出去，进而维持内外桶温度恒定，因此根据能量守恒定律与式(4)得到搅拌产热速率为：

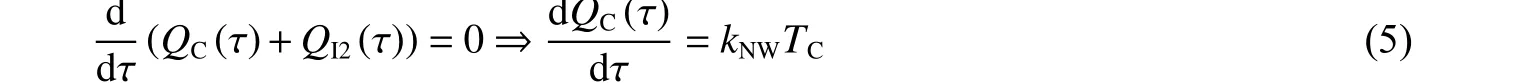
式中：QC(τ)为搅拌热，且产热速率恒定（QC(τ)、QI2(τ)在初始调温阶段的计算起点均为该阶段起始时刻）。

在恒温法中，外桶水温度TW进入初期阶段后是一个常量。而在绝热法中，外桶水温度TW(τ)需跟踪内桶水温度的变化，且与内桶水温度的关系为：

外桶水温度表达式为TW时，表示该温度为常量；表达式为TW(τ)时，表示该温度为变量。

2.2 爆炸产物向内桶系统的传热分析

爆炸产物向内桶系统的传热分为两个阶段，第一阶段是炸药爆轰与爆炸产物飞散过程对内桶系统辐射传热，第二阶段是爆炸产物充满爆热弹后对内桶系统传热。

宋浦等[12]通过含铝炸药光辐射实验研究指出，炸药爆轰及无氧燃烧反应阶段的热辐射基本为可见光辐射，而可见光辐射总能量仅占总爆热的0.02%，因此，第一阶段传热对总爆热的影响可忽略不计。

第二阶段中：爆炸产物充满爆热弹后的极短时间内，它在爆热弹内剧烈振荡（压强振荡时间不超过20 ms[2]），此阶段爆炸产物与爆热弹壳体的传热方式为强对流传热；随着爆热弹内压强振荡趋稳，爆炸产物与爆热弹壳体的传热方式转为弱对流传热；当爆炸产物完全稳定后，爆炸产物与爆热弹壳体之间的传热方式变为热传导。因此，弱对流传热与热传导是爆炸产物向内桶系统传热的主要方式。

由于爆热弹壳体（钢材质）的导热系数高、壳体较薄，弱对流与热传导状态的爆炸产物导热系数相对较小，内桶水对流强度不高，因此，爆热弹壳体的温度场沿壳体径向近似为线性[11]。

由于爆热弹壳体导热良好且较薄，爆炸产物初温非常高[13]，因此，局部升温阶段时间很短。而外桶系统传热与搅拌产热速率很小，因此，该阶段外桶系统传热量与搅拌产热量均近似为零，内桶水及其外壳温度在该阶段近似恒定，进而得到该阶段爆热弹壳体温度场分布：

图2 爆炸产物的传热过程Fig.2 Heat transfer process of explosive product

式中：t(x,τ)为在时刻τ 距离爆热弹壳体内壁（径向）x处的温度，TE(τ)为爆炸产物在时刻τ 的温度，L为爆热弹壳体的平均厚度。

由式(7)，局部升温阶段爆热弹壳体吸收的热量为：

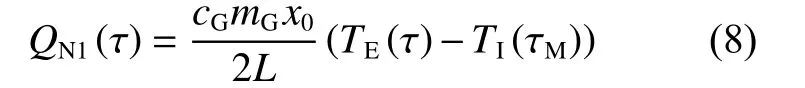
式中：QN1(τ)为时刻τM至τ 爆炸产物的传热量，cG、mG分别为爆热弹壳体的比热容、质量。

炸药爆轰后的氧化、燃烧等二次反应时间极短（无氧环境不超过0.3s[2]），因此，二次反应阶段爆炸产物因传热导致热量损失可忽略，可视为瞬态升温过程，随后爆炸产物一直处于放热过程，因此有：

式中：cZ、mZ分别为爆炸产物的比热容、质量。

在全局升温阶段，根据傅里叶传热定律，爆炸产物向内桶系统传热的热流量ФN1(τ)正比于爆热弹壳体的温度场梯度：

3 量热计传热模型

3.1 初期阶段的传热模型

初期阶段（绝热法没有初期阶段）只有外桶传热与搅拌热引起内桶系统的升温，由于外桶传热与搅拌产热速率低，因此，可认为此阶段爆热弹壳体、内桶水及其外壳同步升温：

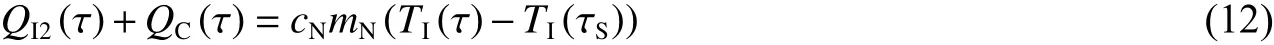
式中：τS为初期阶段起始时刻；cT、mT分别为内桶水及其外壳的比热容、质量，cN、mN分别为内桶系统的比热容、质量。cN、mN满足：

将式(5)、(12)代入式(4)，得到初期阶段量热计的传热学方程：

解式(14)，再结合式(12)，得到内桶水在初期阶段的理论温升曲线：

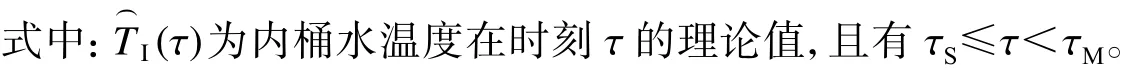
3.2 主期与末期阶段的传热模型

由于局部升温阶段时间很短，因此全局升温阶段可近似为主期与末期阶段。根据能量守恒定律，该阶段爆炸产物传热、搅拌产热、外桶系统传热共同引起爆热弹壳体、内桶水及其外壳的温升：

式中：PG为爆热弹壳体热容占内桶系统热容的比例。PG为：

根据式(18)、(20)～(21)易证，λ2＜λ1＜0。

联合式(4)～(6)、(9)、(11)、(16)，得到绝热法在全局升温阶段的传热方程：

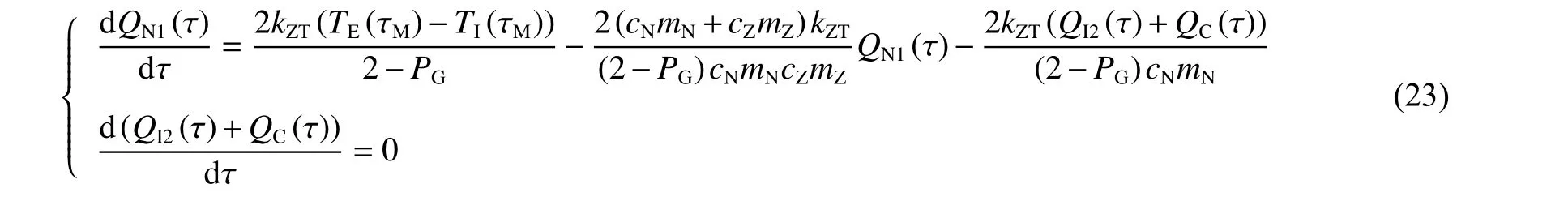
解式(23)，再结合式(9)、(10)、(16)，得到绝热法在全局升温阶段内桶水理论温升曲线：

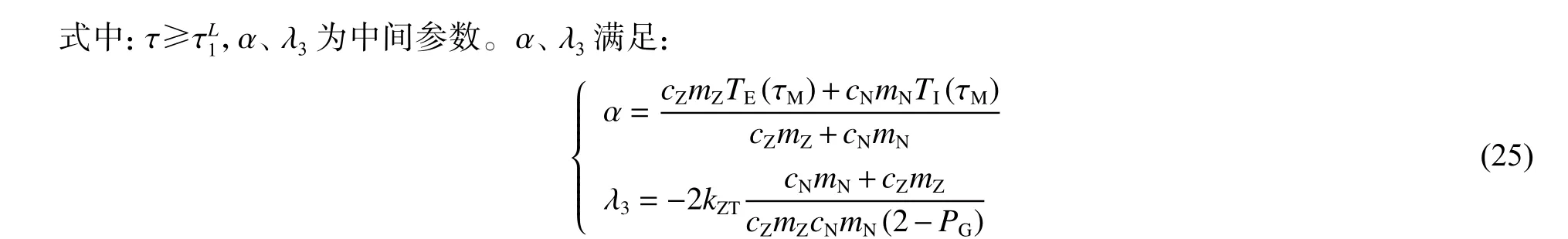
4 快速系统辨识方法的提出

系统辨识方法是通过系统的输入输出来反推系统结构或辨识系统参数，参数辨识的目的是，通过参数估计得到的模型是在选定的模型类中最好的。基于该方法，提出恒温法测爆热的快速系统辨识方法（以下简称快辨识法）的思路如下：首先，分别基于内桶水在初期阶段、主末期阶段的温升曲线辨识参数kNW/(cNmN)、u1、λ1、λ2；然后，基于隔离易受干扰参数λ1的思路快速辨识修正温升与爆热。

4.1 各测量阶段的参数辨识

量热计如在初期阶段出现故障，由于炸药未起爆，尚有调整与修复的机会，因此，初期阶段的全部测量数据可用于参数辨识；如在主末期阶段出现故障，由于炸药已起爆，很难有调整与修复的机会，因此，主末期阶段只有故障前的测量数据可用于参数辨识。

考虑到内桶系统比热容很大，而内外桶之间绝热措施良好，因此有kNW/(cNmN)≈0，根据泰勒展开，内桶水在初期阶段的理论温升曲线（式(15)）可近似为线性方程：

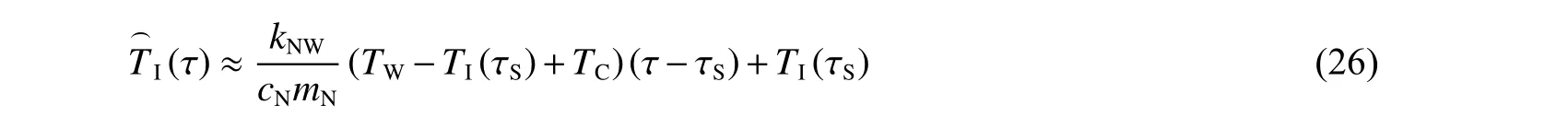
对内桶水在初期阶段的实测温升曲线进行线性拟合，得到拟合方程：

式中：k1、k2、ε(τ)为拟合方程的一次项系数、零次项、拟合残差。

对比式(26)～(27)可得，基于初期阶段测量数据辨识参数kNW/(cNmN)为：

利用内桶水在主末期阶段理论温升曲线（式（19））拟合实测温升曲线，以拟合残差均方根最小化为目标来辨识系统参数，得到基于故障前测量数据辨识中间参数u1、λ1、λ2的目标函数为：

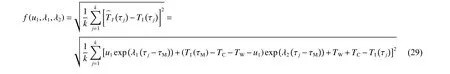
式中：τj为起爆后的第j个采样时间点，k为起爆至测量时间τ 的采样点个数。

注意，考虑局部升温阶段时间很短，因此，式(29)中将τ1L替换为τM对辨识精度影响可忽略。

由式(19)、(21)可知，λ1为内桶水温升曲线慢变特征量，且kNW/cNmN≈0时，有λ1≈0，即内桶水温升曲线慢变特征不显著，因此，λ1的辨识结果易受到快变过程与温度波动的干扰。多次模拟表明，基于目标函数（式(29)）最小化辨识λ1时，如测量时间较短且λ1无约束，则内桶水温度辨识曲线的全局拟合精度较差，目标函数衰减速度很慢。因此，为了加快算法收敛速度，需对λ1的取值范围进行约束。考虑到kNW＜＜kZT，再根据式(20)～(21)可得：

再考虑式(30)中kNW＜＜kZT、cZmZ＜＜cNmN，本文中给出一个相对宽松的约束条件：

因此，基于系统辨识的思想，本文中提出通过求解目标函数（式(29)）在约束条件（式(31)）下最小值的策略来辨识中间参数u1、λ1、λ2。

4.2 修正温升与爆热的快速辨识

首先介绍绝热法修正温升的辨识方法，然后借鉴其思路给出恒温法修正温升的辨识方法。

根据式(23)计算结果可以证明，绝热法中爆炸产物向内桶系统的总传热量为：

再根据修正温升的定义，结合式(25)，可以证明，绝热法修正温升在测量时刻τ 的辨识值为：

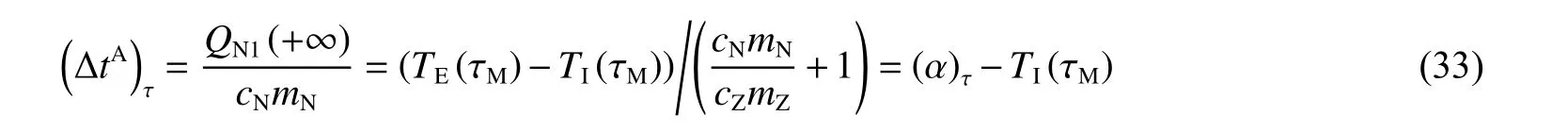
注意，本文中用(*)τ表示参数*在时刻τ 的辨识值。

因此，绝热法辨识思路为，利用内桶水理论温升曲线（式(24)）拟合实测温升曲线辨识参数α，再根据式(33)、式(3)计算修正温升、爆热。由于参数α 反映温升快变项的幅值，因此，α 收敛很快，爆热辨识值收敛也很快。

而对恒温法测量数据多次模拟表明，增加约束条件（式(31)）虽有利于提高温升曲线的全局拟合精度，但λ1辨识值受温度快变过程与温度波动的影响仍会出现频繁的振荡现象，进而降低了修正温升与爆热辨识值的收敛速度；然而，爆炸产物放热结束时，如内外桶温差较大，则内桶水温度将经历一个长时间的慢变过程，慢变过程的累积影响也是不可忽略的，不可简单地按绝热过程（λ1=0）辨识内桶水的修正温升。

综上所述，基于隔离参数λ1振荡影响，兼顾考虑恒温法测量中普遍存在的内桶水温度长时间慢变过程，参考绝热法修正温升辨识公式(33)，提出恒温法修正温升在测量时刻τ 快速辨识算法：

将式(34)代入式(3)，即可得到炸药爆热的辨识值。

4.3 辨识误差分析

考虑kNW＜＜kZT，将式(22)代入式(34)可得，恒温法修正温升的辨识值近似收敛值为：

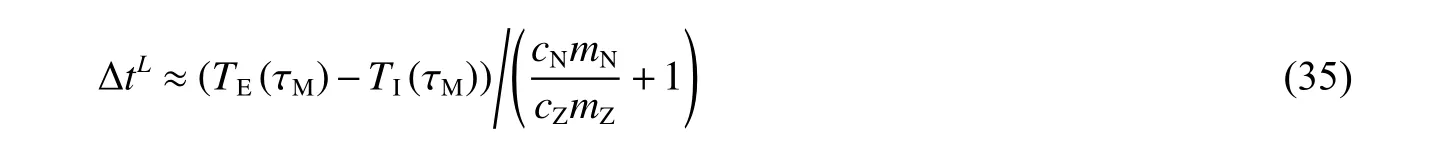
比较式(33)与式(35)可知，恒温法与绝热法修正温升辨识值的收敛值一致。

根据爆热的经典计算公式(1)～(2)，结合主末期阶段的温升曲线（式(19)），及起点温度与温升速率的理论辨识值，可证明经典方法修正温升理论值为：

根据快辨识法与经典方法得到的修正温升的相对误差，来评价爆热辨识值计算精度，令：

代入式(35)～(36)，计算可得：

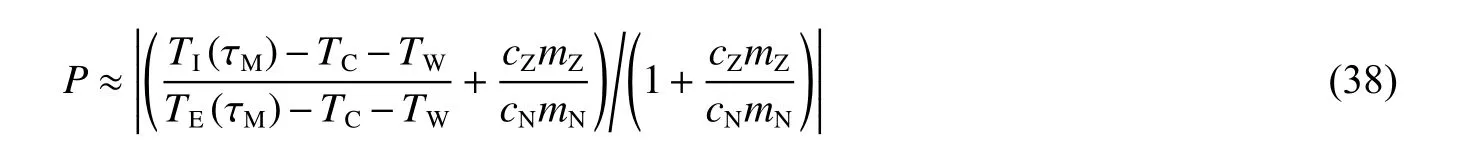
由于TE(τM)＞＞TI(τM)、cNmN＞＞cZmZ，因此有P≈0，即快辨识法与经典方法的爆热计算精度相当。

从式(34)～(35)、图3可知，恒温法修正温升辨识值收敛特性不受参数λ1的直接影响，且参数u1反映温度快变幅值，受干扰小。因此，综合前述分析，爆热的快速辨识方法具有较高的收敛速度、精度与稳定性。

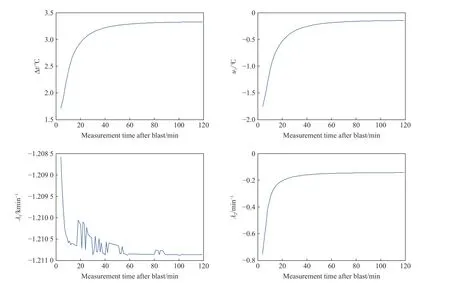
图3 实验模拟的各参数辨识值Fig.3 Identified values of each parameter in an experiment simulation

5 实验分析与讨论

爆热测量的经典算法与系统辨识算法虽基于相同的传热学模型，但误差机制却有较大的不同。经典算法本质上计算爆炸产物向内桶系统传热量的积分，其计算精度取决于爆炸产物放热的完全性，因此，需要尽可能长的测量时间和尽可能小的外界累积干扰；而系统辨识算法本质上是基于爆炸产物向内桶系统传热特征量估计的传热量预测，其计算精度取决于传热模型的吻合性与特征量辨识的精确性。一般认为，测量时间足够长时，经典算法得到的爆热值能较好地收敛于真实值。本节以经典方法为基准，通过实验数据检验快辨识法的性能，并提出可用于实际测量中收敛时间点判断的实验判据。

利用恒温法测量设备进行爆热测量。实验测量真空条件下炸药爆热，实验步骤参照GJB 772A—97中方法701.1，但为了降低测量误差，初期、主期、末期3个阶段分别延长为21、100、20 min。考虑炸药爆热值主要在4～9 kJ/g 范围，为了检验辨识方法的普适性，选取了8个基本均匀分布在该爆热范围内的典型炸药（见表1）进行测量与模拟分析，其中，样本1～4为高爆热炸药，样本5～8为含TATB的炸药。

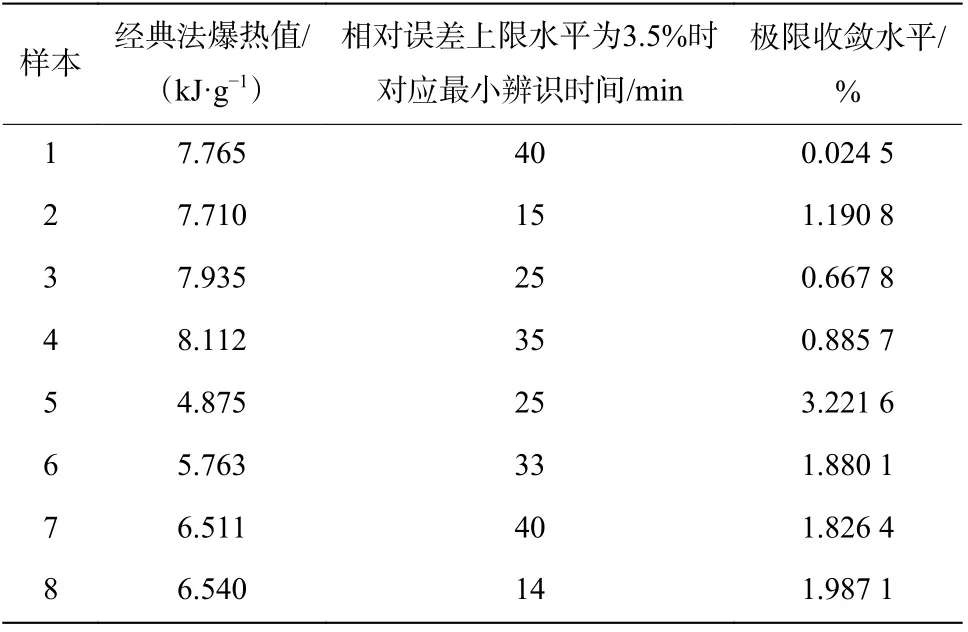
表1 爆热辨识值的收敛情况Table1 Convergent statusof system identify value of explosion heat

为了便于评价爆热辨识值收敛效果，定义如下参数。

（1）爆热辨识值相对误差为：

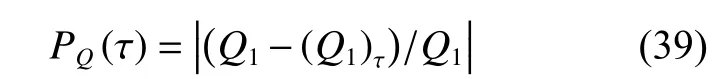
式中：Q1为测量结束后经典方法的爆热计算值，(Q1)τ为测量时刻τ 系统辨识方法的爆热计算值。

（2）相对误差上限水平、相对误差平均水平为时刻τ 后爆热辨识值相对误差的最大值、平均值。

（3）极限收敛水平取相对误差上限水平最小值。

选取表1中样本1的实验数据进行具体分析，如图4所示。初始调温阶段内外桶温差TC=0.552℃（TC取决于搅拌产热速率），外桶升温结束后的温度TW=27.019℃。炸药于85 min 起爆，起爆后，内桶水温度经历了一个快速上升的过程，理论上讲，测量时间足够长时，内桶水温度将达到TW+TC。

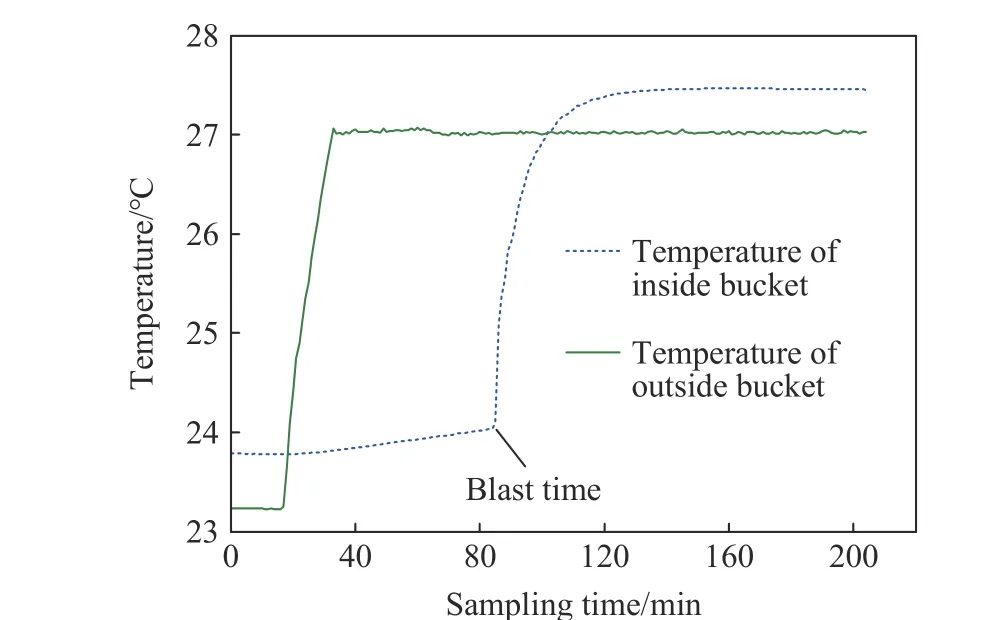
图4 内外桶温度随采样时间的变化Fig.4 Variationsof inner and outer barrel temperature with sampling time

样本1各参数收敛情况如图3所示，参数λ2、u1收敛稳定，参数λ1振荡明显，但修正温升Δt有效地隔离了参数λ1的振荡影响，起爆40 min 后变化量仅为0.11℃，从而检验了本算法的收敛稳定性。

将各参数辨识值代入式(19)，即得到主末期内桶水温升的拟合曲线，拟合残差均方根变化情况如图5所示。随着辨识时间的增加，拟合残差均方根迅速而稳定地减小，在起爆后27 min 即达到0.2℃量级，从而检验了本算法对内桶水温升变化的预测能力。

图5 内桶水主末期温度曲线的拟合残差均方根Fig.5 RMSof fitting residualsof inner barrel water temperature curve at main and end stage

样品1的模拟表明，以测量结束后经典方法爆热计算值7.765 kJ/g 为参照，爆热辨识值在起爆后40、43、51 min 快速稳定地收敛至3.5%（7.498 kJ/g）、3%（7.537 kJ/g）、2%（7.613 kJ/g）的相对误差上限水平，并最终达到了0.024 5%（7.764 kJ/g）的极限收敛水平，如图6～7所示，从而检验了本算法的收敛速度与精度。

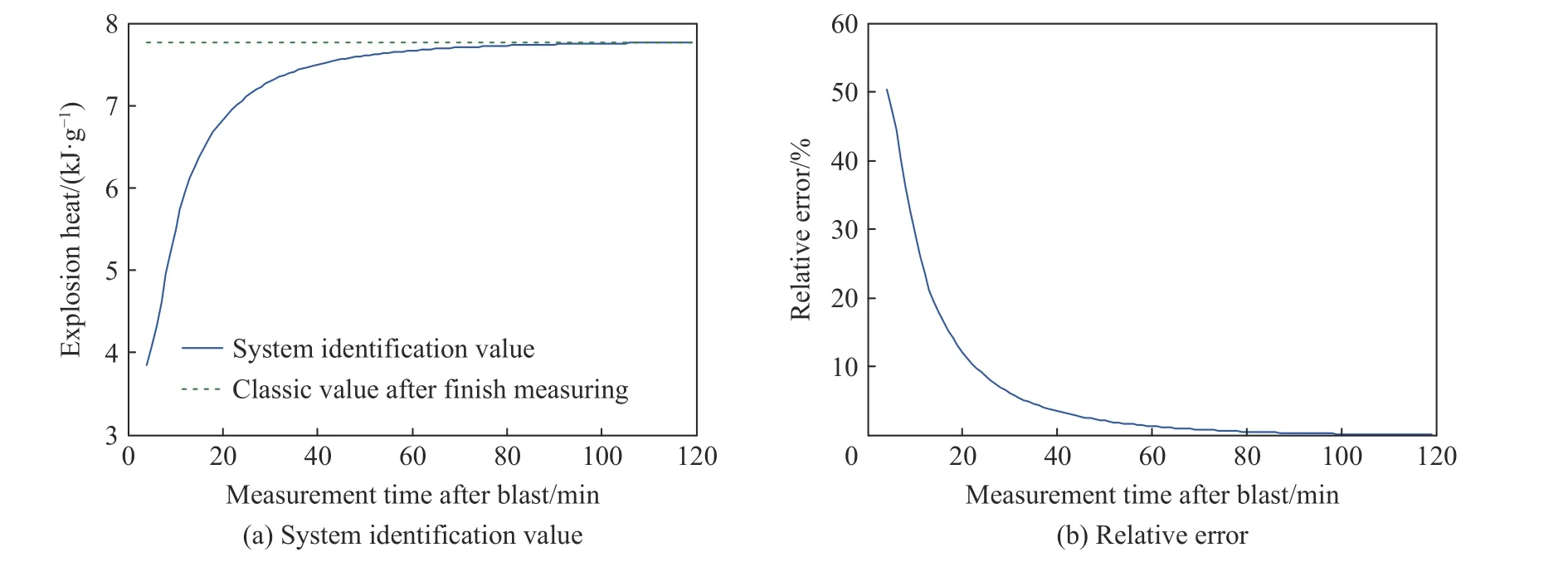
图6 爆热系统辨识值和相对误差随测量时间的收敛Fig.6 Convergence rule of system identify valueand relativeerror of explosive heat with measurement time

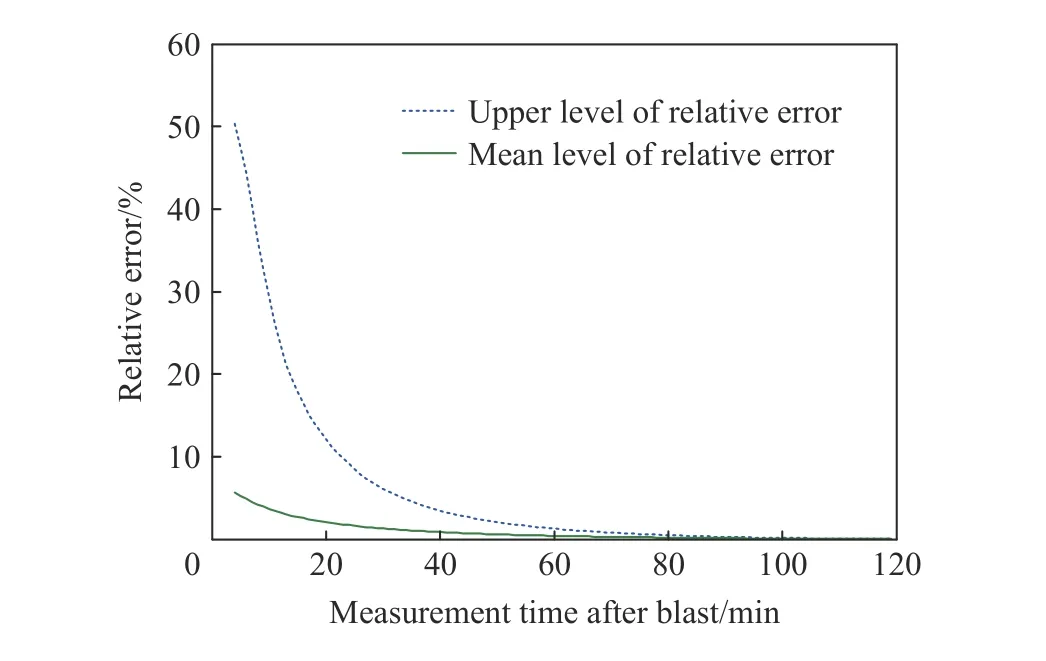
图7 相对误差上限水平和平均水平随测量时间的变化Fig.7 Variationsof upper limit level and average level of relative error with measurement time

对炸药的恒温法爆热测量数据应用快辨识法进行模拟分析，各炸药爆热的经典值、辨识值收敛至3.5%相对误差上限水平所需最小时间、极限收敛水平等参数计算结果，见表1。

由表1可见：快辨识法得到的爆热值能快速地（一般不超过40 min，即主末期总时间的1/3）收敛至经典值3.5%的相对误差上限水平内；除样品5极限收敛水平为3.221 6%，其他样本还能在起爆后50 min内进入2%的相对误差上限水平。这验证了本算法的普适性。根据式(38)，样品5收敛相对较差的原因可能是炸药爆热值较低，对应爆温也较低，导致收敛精度略差。

为了提高本方法的可操作性，给出测量过程中爆热辨识值的收敛情况，根据修正温升辨识值收敛时的慢变特性，并且研究发现，线性拟合测量时刻τ 及前14 min（共15个测量点）内的修正温升辨识值-时间曲线的直线斜率绝对值（记为J1）、拟合残差均方根（记为J2）特征量能较好地反映时刻τ 的数据变化速率与波动性。因此，本文中利用统计方法分析了各样本的这两个特征量的分布规律，得到了实验判据：如J1≤0.008℃/min，且J2≤0.006℃，则爆热辨识值在测量时刻τ 的相对误差上限水平小于3.5%。

模拟结果表明，本实验判据得到的收敛时间略大于理论收敛时间且判断误差不超过20 min，具有较好的可靠性。但考虑本实验判据所统计的样本量较小，还需要开展大样本实验进一步完善。

6 结 论

快辨识法在确保收敛精度的前提下，有效地压缩了测量时间，降低了系统故障导致测量失败的风险；或者说，当出现系统故障时，经典测量方法失效的情况下，快辨识法仍能得到一个不算差的估算结果。因此，快辨识法可作为经典方法的备用方案。通过理论与实验研究，主要获得以下结论。

（1）快辨识法只辨识中间参数kNW/(cNmN)、u1、λ1、λ2，而不辨识目标参数TE(τM)、kZT/(cNmN)、kZT/(cZmZ)，避免了参数λ1振荡通过目标参数传导至修正温升辨识值，算法的收敛速度与稳定性有了显著提高，但由于收敛值与经典值存在偏差，收敛精度会略有损失。

（2）当kNW/(cNmN)=0时，快辨识法的修正温升表达式退化为绝热法修正温升表达式，因此，快辨识法可拓展至绝热法的爆热辨识。

（3）对样本1 模拟结果表明，中间参数λ2、u1收敛稳定，中间参数λ1虽存在明显振荡，但修正温升Δt有效地隔离了λ1的振荡影响，并在起爆后40 min 收敛于0.11℃波动水平，验证了快辨识法的收敛稳定性。

（4）对样本1模拟结果表明，对内桶水在主末期温升曲线拟合残差均方根在起爆后27 min 即达到0.2℃量级，爆热辨识值在起爆后40 min 即收敛至3.5%的相对误差上限水平，并最终达到了0.0245%的极限收敛水平，验证了快辨识法的收敛速度与精度。

（5）对爆热值分布在4～9 kJ/g 的8 个炸药样本模拟结果表明，爆热辨识值可快速地（一般不超过40 min，即主末期总时间的1/3）收敛于经典值3.5%的相对误差水平内，验证了快辨识法的普适性。

（6）提出了在测量过程中实时判断爆热辨识值收敛情况的实验判据，且收敛时刻判断误差不超过20 min。