最大期望模拟退火的贝叶斯变分推理算法

刘浩然 张力悦 苏昭玉 张 赟 张 磊

①(燕山大学信息科学与工程学院 秦皇岛 066004)

②(河北省特种光纤与光纤传感重点实验室 秦皇岛 066004)

③(北京市机电研究院 北京 100027)

1 引言

在机器学习中，贝叶斯推理已经成为求解不可观测变量后验概率的重要方法，它类似最大期望算法。当模型更为复杂时，贝叶斯精确推理求解具体的参数分布时间开销巨大，而许多时候对于复杂模型的参数分布精确求解不是必要的，而推理的真正目的是得到参数的期望或者近似分布，以了解数据遵循分布的规律[1,2]。精确的贝叶斯推理表现出计算量随变量增加呈指数增长以及计算时间也迅速增加的问题，近似贝叶斯推理针对于此类问题有较好的方法，其中基于蒙特卡罗抽样(Markov Chain Monte Carlo, MCMC)[3]的随机近似算法通过采样的方式计算参数后验概率，MCMC算法提供了从目标分布渐进地生成精确样本的精确率保证，然而MCMC方法在数据量较小时，无法保证采集过程的准确率，算法的结果较差，算法会随着数据量和采样量的增大，其结果越来越好，但与此同时计算消耗和时间消耗也越来越大，而另一种确定性近似算法即变分推理算法[4]将求解隐参数后验问题转化成变分优化问题，通过迭代找到较优的后验分布解，这种方法在应对更为复杂的模型下，表现出良好的计算效率[5]。

变分推理算法广泛应用于计算机科学、模式识别、图像处理、卡尔曼滤波、战场决策等领域[6–9]。近年来，许多学者深入研究变分推理算法并提出了有效的改进方案，以解决其存在的相关问题。Gianniotis等人[10]使用梯度下降优化变分参数实现模型似然下界重新构建，通过循环迭代得到模型参数后验分布，算法具有较强的泛化能力，可应用于多种场景，如贝叶斯线性回归、贝叶斯多目标分类、概率图像去噪等，但算法在引入梯度下降优化似然下界时加重了原算法的局部最优问题。Shekaramiz等人[11]提出使用贪婪策略筛选出支持度子集进行变分推理，该算法能有效地防止算法过拟合，但算法主要针对稀疏的贝叶斯学习，在数据样本属性较多时，该算法无法得到较好的模型参数后验结果。Katahira等人[12]将最大熵引入确定性退火算法控制退火过程，算法得到相对原变分算法更优的结果，但其随机初始先验对最终结果影响较大。Tabushi等人[13]使用非线性最大化非广延统计力学的Tsallis熵提出了广义确定性退火最大期望(Generalize Deterministic Annealing Expectation-Maximization, GDAEM)算法，通过控制参数得到全局较优解，由于控制参数设置的问题，收敛效率有待提升。Salimans等人[14]提出了基于马尔科夫链的变分近似，该算法将两种近似方式有效结合，实现了速度和精度的相对平衡，但算法针对复杂的模型时，依然表现出采样时间消耗大的问题。

本文针对部分算法对求解模型参数后验分布时间消耗长、收敛精度低的问题，提出一种基于最大期望模拟退火的贝叶斯变分推理算法(Expectationmaximization and Simulated annealing for Variational Bayesian Inference, ES-VBI)，将双重最大期望(Expectation-Maximization, EM)策略应用于初始先验的生成，将模拟退火策略的逆温度参数用于似然下界的优化，最终返回算法迭代最优解，利用收敛性准则理论分析算法的收敛性，将该算法应用于混合高斯分布实例的实验仿真，说明本算法的优势。

2 问题描述

变分推理经常被用于计算模型的参数后验分布问题，通过变分法将求解模型参数后验问题转换为变分自由能最大化迭代寻优问题，最终返回全局较优解，即为最合理的近似模型参数后验分布。本文提出的算法针对初始先验和变分自由能在寻优过程中进行优化：(1)在保证算法速率的情况下，满足模型参数的后验分布的近似度最高；(2) 尽量降低算法对初始先验的敏感性，保证算法具有对全局有效的初始先验，防止算法过早地陷入局部最优。针对变分推理过程中的上述特点，给出如下推理模型。

2.1 参数描述

本文给出3个定义描述推理模型。

(1)观测变量和不可观测变量。贝叶斯网络中，变量类型分为观测变量和不可观测变量，其中观测变量是直接可观察或可采集的变量；不可观测变量是不可直接观察或不可直接采集的变量，不可观测变量包括潜变量和模型参数，潜变量用于解释观测变量，可以看作其对应观测变量的抽象和概括。模型参数是描述模型数据自身存在规律的参数。

(2)库尔贝克距离(Kullback-Leibler, KL)。衡量假设的近似分布q与真实分布p之间差异的量称为KL散度，也称KL距离[15]。其表达式如式(1)所示

其中，KL(q‖p)表示近似分布q与真实分布p的KL距离；W表示模型参数集合(隐变量集合)；X表示观测变量数据。

在变分推理中，通过随机赋值或者其他赋值方法给出一个初始先验分布q，假设q是精确条件的候选假设分布，算法将KL(q‖p)不断优化达到最小，达到假设分布与真实分布的差异无限接近于0，得到对应的q为

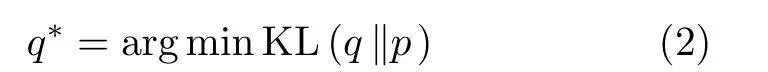
(3)证据下界(Evidence Lower BOund, ELBO)。观测变量数据似然对数lgp(X)与KL距离的差值称为证据下界(ELBO)[16]。在贝叶斯变分推理过程中，初始计算参数后验分布时，根据贝叶斯公式，将数据分布表示为似然对数的形式lgp(X)，经过化简得到ELBO与lgp(X), KL距离的关系表达式

其中，L(q)称为证据下界，即ELBO。此时lgp(X)是常数并保持不变，要使KL距离最小，则使ELBO达到最大，KL距离与ELBO的关系如图1所示。由于在变分推理过程中，最小化KL距离无法通过式(1)直接计算，故通过最大化ELBO(即最大化L(q))，最终得到最优的近似分布q∗＝arg maxL(q)。

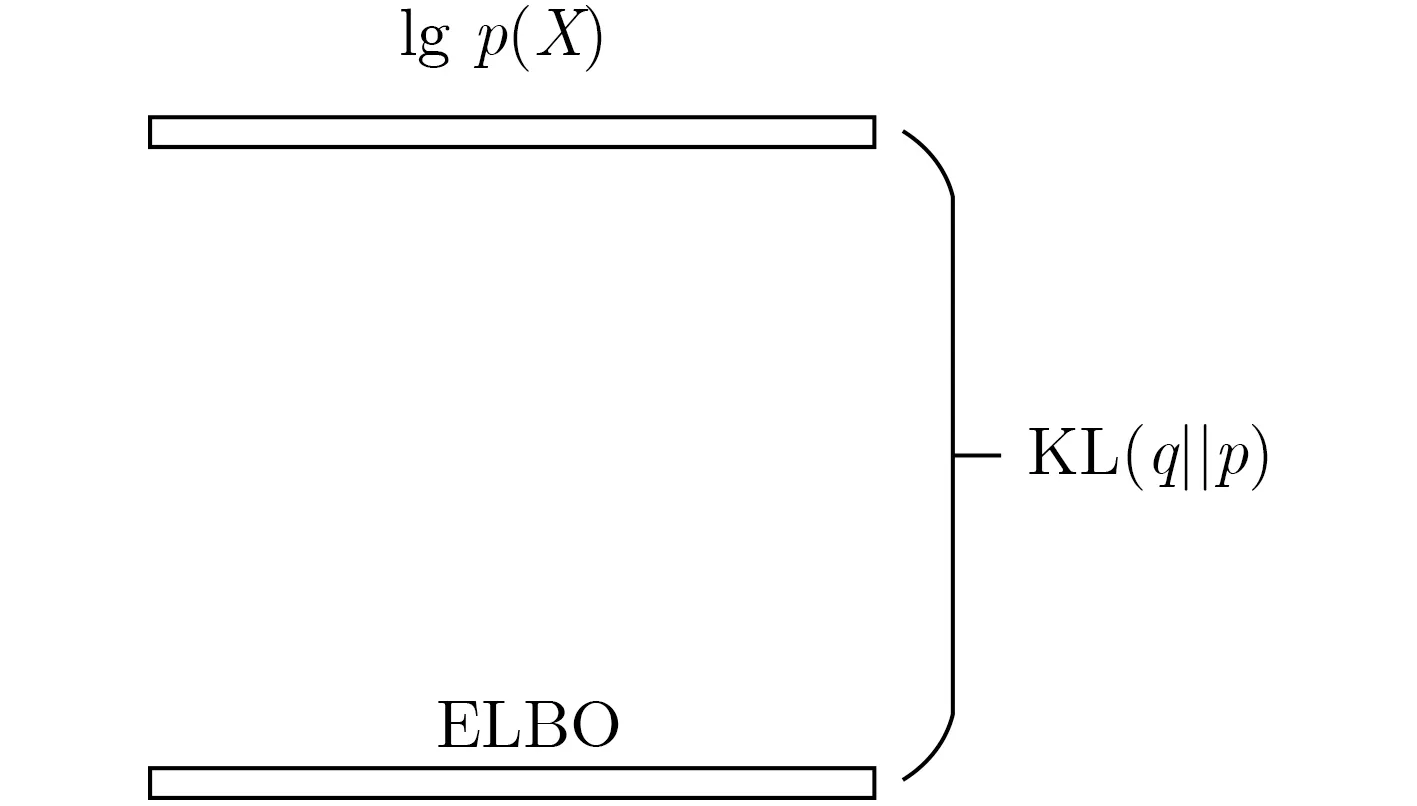
图1 KL距离与ELBO的关系

2.2 模型后验分布描述

设推理模型的观测变量集合为X＝{x1,x2,···,xn}，其中xi,(i＝1,2,···,n)表示第i个观测变量，n表示观测变量的总数；设不可观测变量集合为模型参数ω和潜变量集合z＝{z1,z2,···,zm}，其中模型参数ω表示描述模型数据在统计模型下的自身存在的规律，理论上最优的模型参数与数据无限接近吻合(拟合度无限接近1 0 0%)，zj,(j＝1,2,···,m)表示第j个潜变量，m表示潜变量的总数。通过对联合分布p(z,ω,X)积分得到观测数据的边缘密度分布(边际似然)p(X)，如式(4)所示

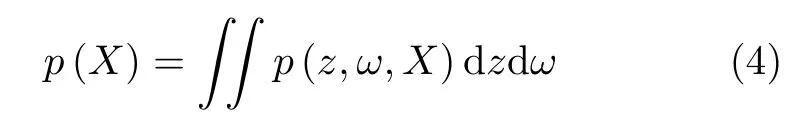
根据贝叶斯定理，z和ω在X上的后验概率表示为

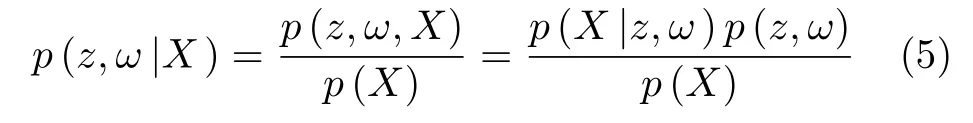
将式(4)代入式(5)，式(5)分母部分表示成边缘密度分布形式

将边际似然等式(式(4))的两边进行对数运算，式(4)进一步分解为

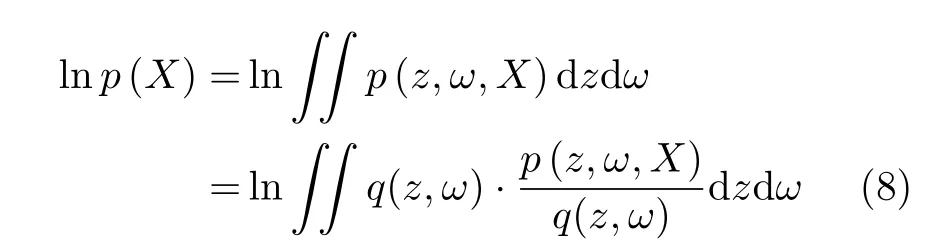
根据Jeason不等式的性质[11]，式(8)等式右边部分存在如式(9)的不等关系

将式(9)中不等式右边部分进一步分解为

2.3 双重EM模型

当前多数的推理算法模型参数初始化都是在一定范围内进行随机赋值操作，但较差的初始化结果，导致算法存在无法收敛到较优值的情况，因此模型参数初始化对初始先验敏感，在增加模型参数的数量时，这个问题显得更加突出。针对先验初始化问题，本算法采用双重最大期望(EM)[19,20]方法，算法在第1次EM算法结果的基础上运行第2次EM算法。在每次循环迭代，在第1阶段，对一组随机初始化数据使用EM算法，得到了第1阶段的模型参数。在第2阶段，针对第1阶段结果再进行第2阶段EM操作，完成ES-VBI的初始化。

求解含观测变量、模型参数的条件概率最大时的模型参数ω,z，以求解ω为例，如式(12)所示

根据对数函数的单调性可得式(12)的等价形式为

算法将最大似然估计准则应用到第1阶段所提供的模型分布。在执行该步骤过程中，选取来源于第1阶段模型分布的数据样本作为第2阶段的初始先验，该阶段的参数分布后验概率为

2.4 模拟退火模型

统计物理学的基本公式有L＝E-TS,(L是变分自由能，E是总能量，T是温度，S是熵)[21]，根据此公式原理，本文在原目标函数(式(11))的基础上引入逆温度参数ϕ＝1/T构建新的目标函数，则此时变分目标函数表示为

逆温度参数有两种特殊情况：如果ϕ→0，则第2项成为整个式子主导，使整个式子最大化相当于使第2个式子最大化，因均匀分布的熵最大，于是整个式子趋于一个均匀分布。如果ϕ＝1，整个式子与式(11)相同，可知得到原始的后验分布，模拟退火对算法的控制逐渐降低。

独立随机变量的联合熵等于各变量熵的和，因此式(19)最右边一项变为式(20)最右边两项，式(20)为

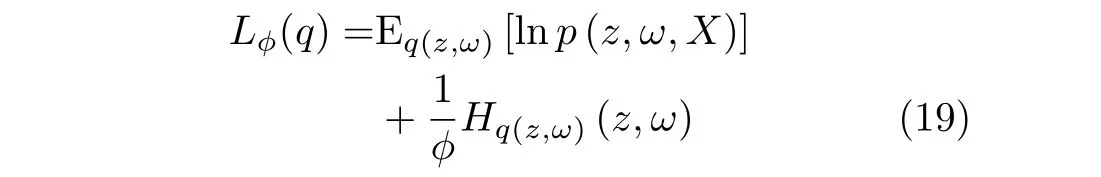
3 算法实现

3.1 算法执行过程

贝叶斯变分(VB)推理的核心是通过构造一个简单分布q去近似待求解的复杂分布p，通过不断缩小它们之间的差异即KL距离，不断增大变分自由能(ELBO)，使分布q与p无限接近，最终求得分布q即为最终的参数分布。

对以式(22)和式(23)构造的拉格朗日式求导并令其等于0(其中F1(z,ω,X,λ1)对qz(z)求导，F2(z,ω,X,λ2)对qω(ω)求导)，得

在原变分推理算法流程中加入双重EM和逆温度参数构建退火循环，可以推导出如表1所示的ESVBI算法。

表1 ES-VBI算法

其中，关于模拟退火的迭代参数const 设置，退火过程是根据控制该参数的取值使得迭代的逆温度参数ϕ逐渐从一个小正数(正向趋于0小于1的数)增加至1，以达到最大终止迭代条件，而且逆温度参数初值也是正向趋于0小于1，所以const的初值应设为大于1，这样ϕ ←ϕ×const才能逐渐从0趋于1。本算法作为DA-VB和SA-VB算法的变体，对于该参数的设置结合了退火算法的整体性能以及大体参照DA-VB的参数const设置 1.1和1.2[12]，通过实验发现两种设置情况下均能达到最终的退火性能，因此本文选择使用const＝1.1。

3.2 算法收敛性分析

定理1 ES-VBI算法中每次迭代增加L(q)，即L(qt+1)≥L(qt)，当且仅当ϕ(qt+1|qt)＝ϕ(qt)时，等号成立。

4 实验仿真

4.1 高斯混合实例和实验设置

高斯模型混合模型是比较经典的包含隐参数的数据模型，我们利用提出的算法从混合高斯模型的数据近似拟合出混合高斯模型中的相关参数的估计值，而且对于在高斯混合模型可以较为准确地衡量算法对模型的鲁棒性和准确性，具有较强的说服力，文献[13]使用了高斯混合模型，文献[14]双变量高斯模型，而且提到可以推广到多变量的混合模型。除此之外在关于变分推理算法对比文献[10–12]中还使用了隐马尔可夫模型、多目标分类、线性回归、逻辑回归等模型进行实验仿真，对比算法的性能，提升算法的可信度。本算法与对比算法属于同类型的推理算法可以针对上述模型进行实验对比，本文由于文章内容限制，仅在高斯混合模型下进行仿真实验，具体如下：本文给出一个高斯混合模型对提出的ES-VBI算法性能进行实验验证，其中该混合模型包含K个高斯分布，以及n个可观测变量xi,i＝1,2,···,n，潜在变量包含K个高斯分布的均值µk,k＝1,2,···,K和n个类别参数ci,i＝1,2,···,n，该模型表示为

为检验ES-VBI算法的迭代效率、收敛精度，将本文提出的ES-VBI算法与A-VI算法(原文中未给出算法具体名称，本文记作A-VI(Advanced-Variational Inference)算法)[10]、OSBL-VB(Ordinary Sparse Bayesiam Learning-Variational Bayesian)算法[11]、DA-VB(Deterministic Annealing-Variational Bayesian)算法[12]、GDAEM(Generalized Deterministic Annealing Expectation-Max-imization)算法[13]、MCVI(Markov Chain Variational Inference)算法[14]在混合模型中进行仿真对比，另外本文使用了一些常用的变分推理的评价量：ELOB和时间t(s)。每个算法在相同数据集下独立运行100次求取平均值为最后的统计结果。实验环境：处理器Intel(R) Core(TM),CPU i7-7700HQ，主频2.80 GHz，内存为16 GB，Windows10 64 bit操作系统，python3.8版本。

4.2 各个算法针对高斯混合模型的实验对比

在混合高斯模型优化中生成器数据为1000时各个算法的ELOB(表示变分自由能，越大越好)和时间t(s)的对比结果如表2所示，它们的迭代过程如图2所示。

图2 各算法迭代过程对比图

由表2数据可得，在6种算法中，ES-VBI算法的变分自由能E L O B 最大，且时间消耗仅比GDAEM算法多一些，但ES-VBI算法的收敛精度高于GDAEM算法，这是由于ES-VBI算法使用了双重EM相对于GDAEM算法的单层EM时间消耗有所增加，但ES-VBI通过双重EM的时间增加代价换来了算法的收敛精度提升。按照ELOB的收敛结果可以将6种算法的收敛精度从大到小排序为ESVBI算法、OSBL-VB算法、A-VI算法、GDAEM算法、MCVI算法、DA-VB算法。而且可以看出ES-VBI算法对比于确定性退火算法DA-VB收敛精度提升较大，说明基于逆温度参数对算法的收敛进行有效的控制，使得算法在迭代寻优过程的目标函数值ELOB更大，在每次迭代中更能优化出较好的模型参数。

表2 各算法ELOB和时间对比

图2显示各个算法在1至100代的目标函数优化图，可以看出ES-VBI算法的初始化过程的结果显然优于其他的随机初始过程结果，通过双重EM模型初始化模型参数使得算法最终的收敛结果较优。其中A-VI算法和OSBL-VB算法由于分别使用了梯度优化和贪婪策略使得其相对另外3种算法最终的结果较好，通过图2中A-VI的迭代线可以看出其在35代以后很难摆脱梯度优化对局部最优的加强影响，使得后期的迭代线较平，算法后期的优化效率较低，且结果精度有待提升。

将高斯混合模型的K设置为5，通过数据生成器生成5000数据样本，对比各个算法对高斯混合模型各个分量的拟合程度，其对比图如图3所示，图3中每种颜色代表一个高斯分量。

图3 各算法针对高斯混合模型拟合图

由各个算法对应的高斯混合模型拟合图，可以看出本文提出的ES-VBI算法拟合程度最好，很且明显优于DA-VB算法和MCVI算法，DA-VB算法通过最大熵控制退火过程，其并不能很好地适应算法迭代的过程，且随机初始先验也影响了最终的收敛结果。而本算法通过模拟退火的逆温度参数有效地控制迭代的过程，相比于DA-VB算法的确定性退火原理在前期和后期都有对目标函数相对较优的寻优效率，使得算法最终的收敛精度较高，拟合混合高斯分布的各个分量较优。

虽然本算法设计了一个改进的变分推理算法，算法对初始化的敏感性降低和迭代过程的有效控制，但所提出的方案仍然没有得到全局最优，只是在模型参数求解方面提供了一个优化的方法，且上述实验验证了提出算法有效性和较优性能。

5 结束语

针对贝叶斯变分推理的初始先验和变分自由能优化两个问题，本文基于模拟退火理论和最大期望理论提出了一种针对降低初始先验影响和变分自由能优化的变分推理方法。通过双重EM模型的构建，使得算法保证近似精度的情况下，进一步提升算法在前期的参数分布质量，通过模拟退火的逆温度参数控制迭代优化过程，进一步提升求解后验分布的精度。通过收敛性理论证明了该推理模型收敛于全局较优解。经过实验仿真证明本文的双重EM模型和模拟退火的逆温度参数的有效性，针对高斯混合模型本文提出算法表现出更好的性能，拟合模型参数的效果较优，同时该算法能够为卡尔曼滤波、贝叶斯神经网络参数求解、图像去噪等提供理论支持。