PMSM直接转矩控制技术的研究

安徽理工大学电气与信息工程学院 岳驰丹 胡 霞

根据永磁同步电机（PMSM）的数学模型，引入直接转矩控制技术（DTC），并在Matlab/Simulink平台搭建仿真模型。仿真结果显示，DTC响应速度快，具有良好的动态性能。

不同于矢量控制（FOC），DTC没有独立的PWM环节，它将电机和逆变器当做一个整体，直接将磁链和转矩的误差信号选择合适的电压矢量，最终作用于电机。所以DTC技术可以用简洁的控制结构实现快速的动态性能。

本文根据PMSM的数学模型，把DTC技术引用于PMSM系统当中，并利用Matlab/Simulink进行仿真搭建，最后得出仿真结果。

1 PMSM的数学模型

实际运用中，为了研究方便，通常忽略PMSM电机中的非理想化因素，做理想化设定条件：

忽略磁路饱和、涡流和磁滞损耗。

三相定子绕组完全对称，转子上无阻尼绕组。

电机中电流为对称三相正弦波电流。

在以上条件下，建立在d-q坐标系下的PMSM数学模型，其定子电压和定子磁链方程为：

其中ud和uq为d、q轴的定子电压；id和iq为d、q轴的定子电流；Rs为定子的电阻；Ld和Lq为d、q轴的电感分量；ψf为永磁体产生的磁链；ω为电机的电角速度。

PMSM电机在旋转d-q坐标系中电磁转矩方程为：

PMSM电机的转子动力学方程为：

其中Te为电机的电磁转矩；Tm为电机的负载转矩；b为电机的阻尼系数；J为电机的转动惯量。

2 PMSM的直接转矩控制系统原理

PMSM的直接转矩系统的原理结构框图如图1所示，它由PI速度调节器、转矩滞环、磁链滞环、开关矢量表、逆变器、磁链和转矩计算、PMSM电机、转速测量等部分组成。

图1 直接转矩控制框图

其控制原理如下：将系统给定的角速度与检检测到的角速度进行对比，得到电机角速度误差信号ωr*，然后误差信号ωr*通过PI速度调节器后输出的数值为转矩给定信号Te*，并与实时反馈的转矩信号Te相比较，从而经过转矩滞环比较器。磁链的控制信号与转矩的控制信号原理相同，最终进入磁链滞环比较器中。滞环比较器的原理是设置一定的滞环宽度，用来减小转矩和磁链信号的误差，使其输出的信号在一个适当并且可接受的区域之内，最终这两者信号在两个滞环比较器中进行有效的调制，最终输出信号经过电压开关矢量表选出适当的开关状态，进而控制逆变器最终驱动永磁同步电机，达到调速的目的。

3 基于Matlab的PMSM直接转矩控制系统建模

根据上述PMSM的直接转矩控制原理，在MATLAB/Simulink的环境中建立PMSM的直接转矩控制系统仿真模型，整体的仿真设计框图如图2所示。系统主要由PMSM电机模块、磁链和转矩计算模块和开关电压矢量表模块等部分组成。

图2 PMSM直接转矩控制仿真系统

3.1 PMSM电机模块

PMSM电机动态模型相对简单，但是在实际的运用之中需要进一步简化，其中常用的方法就是坐标变换，把三相静止坐标转化为两相同步旋转坐标系。新版本的MATLAB/Simulink已提供PMSM电机仿真模块，可以直接运用。

3.2 磁链和转矩计算模块

在获取同步旋转坐标系下的定子电压和电流之后，通过公式(1)计算磁链的大小。转矩的数值则由公式(2)计算得出，最终这两者信号进入电压开关矢量选择表，选取合适的电压矢量。

3.3 开关电压矢量表模块

开关电压矢量表是根据转矩和磁链滞环的开关状态，以及磁链所在的位置，从而控制逆变器输出电压，最终驱动PMSM。

4 PMSM DTC系统仿真

选用此表贴式PMSM电机作为仿真电机，电机系统参数如表1所示。

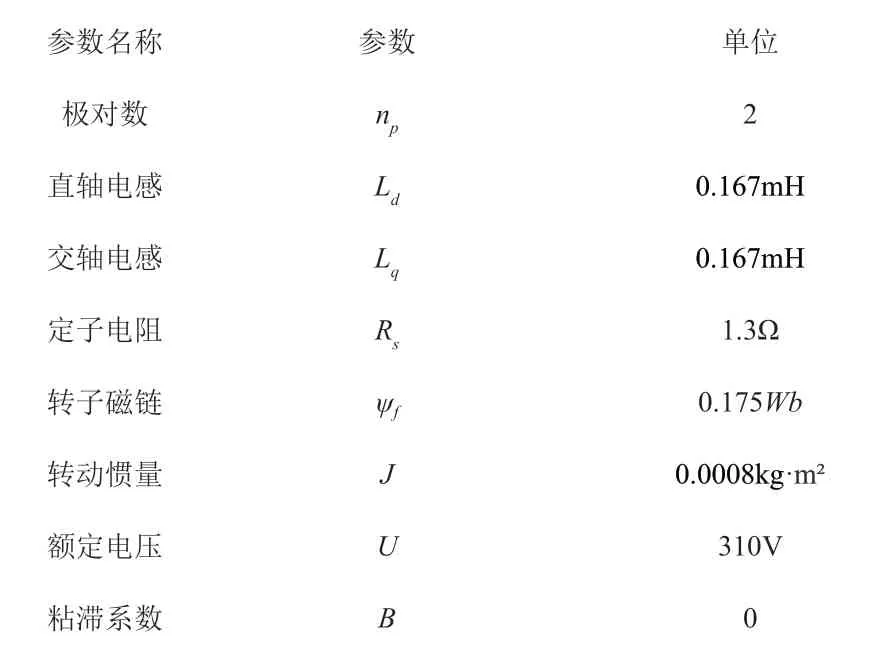
表1 电机系统参数

仿真条件设置为：初始转速为700r / min，初始时刻的负载转矩TL= 0N●m，在t= 0.2s时负载转矩TL= 2N●m，仿真时间为0.4s。磁链轨迹图、转速、转矩的变化曲线图分别如图3～图5所示。

图3 磁链轨迹

图5 转矩的变化曲线

5 实验结果分析

仿真结果显示，在整个仿真的过程中，图3定子磁链的运动轨迹近似成圆形，并且波动很小，说明PMSM电机周围的旋转磁场较好的达到了我们预期的圆形磁场。图4所示的转速曲线可以看出，当PMSM电机从零上升到给定转速700r / min时，虽然在最开始时电机转速有一些超调量，但依旧具有较快的相应速度，并且顺利达到设定转速，表现出较好的动态性能。同时图5所示的转矩的变化曲线表明，在0.2s给定负载突变后，转矩能很好的随之改变，证明直接转矩控制技术可以较好的运用于PMSM电机系统中。

图4 转速的变化曲线

结论：本文研究了PMSM DTC系统的方法和控制原理，并运用Matlab/Simulink软件搭建了仿真模型，进行了仿真实验。仿真结果显示，PMSM直接转矩控制系统响应速度快，鲁棒性强，具有一定的实际应用意义。