基于自适应无迹卡尔曼滤波的汽车状态参数估计

石志伟， 任师通， 魏民祥， 查曰珩

(1.山东理工大学 计算中心， 山东 淄博 255012；2.南京航空航天大学 能源与动力学院， 江苏 南京 210016；3.江苏省文化馆， 江苏 南京 210016)

对汽车主动安全性进行分析时，获取汽车行驶过程中的状态参数尤为重要。用于汽车关键状态参数估计的算法主要有卡尔曼滤波算法、粒子滤波算法、滑模观测器算法、鲁棒观测器算法和龙贝格观测器算法等。其中粒子滤波算法易出现因密度函数建立不准确而导致粒子退化的现象；滑模观测器算法依赖传感器的精度和性能，否则易产生抖振现象；鲁棒观测器算法在有些情况下易产生低估估计偏差，从而引起算法发散；龙贝格观测器算法的计算过程较复杂，不易满足车辆估计算法的实时性要求；卡尔曼滤波算法(KF)计算简单、收敛快速，在汽车状态参数估计中得到广泛应用。

汽车是一个强非线性系统，而卡尔曼滤波仅能对线性系统进行处理，在标准卡尔曼滤波算法的基础上开发出扩展卡尔曼滤波算法(EKF)和无迹卡尔曼滤波算法(UKF)来处理非线性系统。扩展卡尔曼滤波算法通过将非线性系统的数学模型在最佳点进行泰勒展开，对非线性函数求解雅可比矩阵，从而将非线性系统线性化。采用该算法进行非线性系统线性化时，只保留一阶系统，对于二阶或更高阶的分量采用舍弃的方法，因而存在一定估计偏差，同时当估计的目标系统非线性较强时，其计算量过大，雅可比矩阵求解复杂，易产生发散现象。而无迹卡尔曼滤波算法摒弃了求解非线性函数的雅可比矩阵，采用构造样本点的方法将整个非线性系统线性化，进而得到一些sigma点，减少了算法的计算量。对于得到的各个sigma点，保证其均值和方差与原始采集数据相同，并将其带入非线性系统中进行无迹变换，通过样本加权求和使其接近高斯分布。基于高斯分布的特点，该算法可精确到三阶均值和协方差，且运算简单，得到的系统稳定。

当前的研究中，大多把观测噪声的协方差矩阵设定为固定值，然而车辆实际行驶过程中，过程噪声和观测噪声是随机产生的，并非固定不变，为更好地对行驶中车辆状态参数进行实时估计，该文将不同时间段的过程噪声和观测噪声设定为不同值，提出自适应无迹卡尔曼滤波(AUKF)算法。

1 三自由度车辆模型

为更好地表达车辆的真实状态，建立具有横向、纵向、横摆3个自由度的车辆动力学模型(见图1)。

Fxf、Fyf分别为前轮在x、y轴方向受到的力；δf为前轮转角；Fcf、Flf分别为前轮受到的纵向力和侧向力；ω为横摆角速度；Fxr、Fyr分别为后轮在x、y轴方向受到的力；Fcr、Flr分别为后轮受到的纵向力和侧向力；a、b分别为质心至前轴和后轴的距离

在x轴方向，车辆的动力学方程为：

(1)

在y轴方向，车辆的动力学方程为：

(2)

在绕z轴的横摆方向，车辆的动力学方程为：

(3)

式中：m表示汽车总质量；Iz表示车辆绕z轴的转动惯量。

2 基于AUKF算法的汽车状态参数估计

2.1 无迹卡尔曼原理

2.1.1 建立汽车状态空间方程和量测方程

非线性汽车系统的状态量为：

x=(ω,β,vx)T

(4)

式中：β为质心侧偏角；vx为车辆的纵向速度。

系统控制输入量为：

u=(δf,ax)

(5)

系统观测量为：

y=(ay)

(6)

根据建立的三自由度汽车模型，得汽车状态空间方程如下：

(7)

量测方程为：

(8)

将过程噪声和测量噪声代入汽车状态空间和量测方程，得：

xk+1=f(xk,uk)+Q

(9)

zk+1=h(xk+1,uk)+R

(10)

式中：xk+1为k+1时刻的状态向量；f为前一时刻状态量与后一时刻状态量之间的映射关系；uk为系统的控制输入量；Q为预测过程中的噪声；zk+1为k+1时刻的观测向量；h为状态向量与观测向量之间的映射关系；R为测量过程中的噪声。

以上2种噪声需满足以下关系，否则易产生协方差矩阵的非正定现象：

E[Q]=0

(11)

E[R]=0

(12)

Cov[R,Q]=0

(13)

式中：E[*]表示*的均值；Cov[*]表示*的方差。

2.1.2 无迹变换

(1) 初始均值和方差的确定：

(14)

(15)

(2) 采集点与各权值计算。1) 采集点。构造2n+1个样本点[见式(16)]。2) 采样点权值计算。由于存在采样的非局部效应，需对各采样点的权值进行一定比例修正，计算得到均值的权值见式(17)，方差的权值见式(18)。

(16)

(17)

(18)

式中：λ为调节参数。

2.1.3 Sigma点的获取

根据式(16)和式(17)，可获取一组Sigma点集，点集中包括2n+1个点，可由向量ζ表示：

(19)

式中：i=0,1,2,…,n。

2.1.4 预测更新过程

当k大于1时，通过加权得到状态的预测值：

(20)

预测更新后得到的均值为：

(21)

式中：q为过程噪声的平均值。

预测更新后获取的方差矩阵的预测值为：

(ζ(k+1|k)-x(k+1|k))T]+Q

(22)

根据测量方程对各个点进行非线性变换：

ζ(k+1|k)=h(ζ(k+1|k))

(23)

得到模型预测更新后的观测值：

(24)

式中：r为测量噪声的平均值。

2.1.5 测量更新过程

系统的输出方差矩阵为：

(ζ(k+1|k)-z(k+1|k)T)]+R

(25)

协方差矩阵为：

(ζ(k+1|k)-z(k+1|k)T)]+R

(26)

卡尔曼滤波增益矩阵为：

(27)

对状态进行更新后的滤波值为：

x(k+1|k+1)=x(k+1|k)+Ka(z(k+1)-

z(k+1|k))

(28)

后验方差矩阵为：

P(k+1|k+1)=P(k+1|k)-

KaPzk+1zk+1KaT

(29)

2.2 自适应无迹卡尔曼滤波原理

在测量噪声和过程噪声为固定值的情况下，无迹卡尔曼滤波算法可完成车辆状态参数估计。但实际上测量噪声和过程噪声具有不确定性。针对实际过程中噪声的不确定性，提出基于Sage-Husa算法理论的自适应无迹卡尔曼滤波算法，该算法可对无迹卡尔曼滤波中的测量噪声协方差和过程噪声协方差进行实时修正。步骤如下：

(1) 按式(30)计算测量噪声的估计平均值。

1|k)]

(30)

式中：bk+1=(1-d)/(1-dk+1)；d为遗忘因子，取0.9。

(2) 按式(31)计算测量噪声的估计协方差。

(31)

式中：ek+1为误差，ek+1=z(k+1)-z(k+1|k)。

(3) 按式(32)计算过程噪声的估计平均值。

qqk+1=(1-bk+1)qqk+bk+1[xk+1-

(32)

(4) 按式(33)计算测量噪声的估计协方差。

RRk+1=(1-bk+1)RRk+bk+1(kak+1ek+1·

(33)

3 仿真验证与分析

为验证文中所建模型与自适应无迹卡尔曼滤波算法的正确性，建立Carsim和MATLAB/Simulink仿真平台，联合仿真结构见图2。

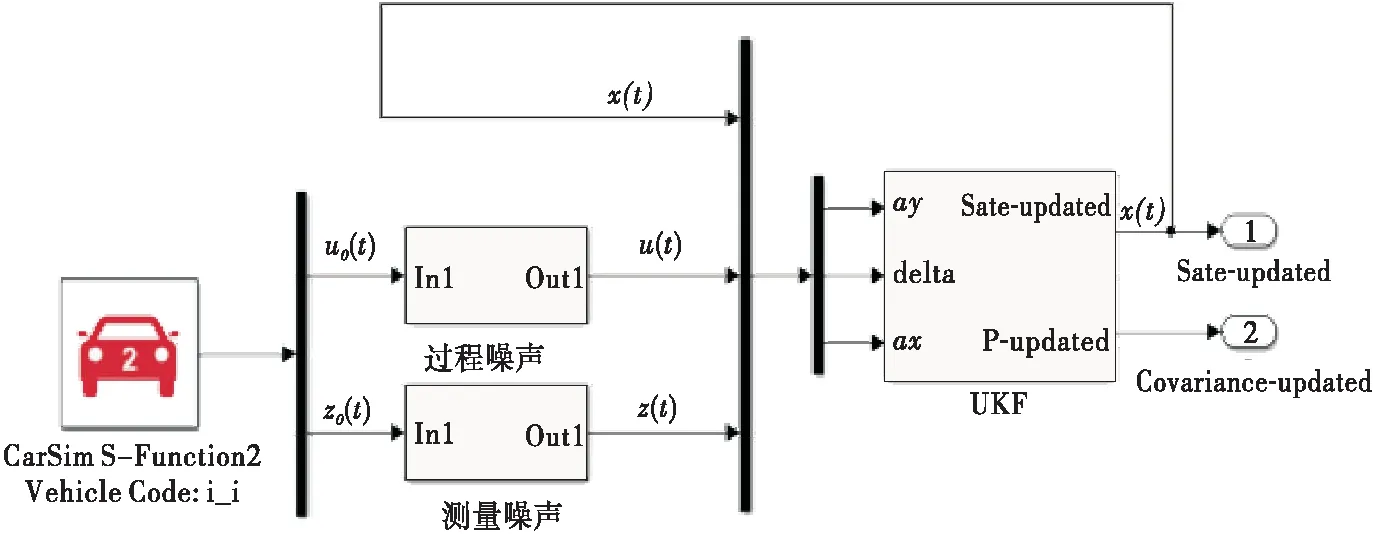
图2 汽车状态参数估计联合仿真结构图

仿真环境选取双移线典型工况、附着系数为0.85的水平沥青路面，仿真车辆选择Carsim中自带车辆，车速设置为72 km/h，采样时间设置为0.01 s，整车质量m为1 500 kg，质心距前轴的距离a为1.55 m，轴距l为3.1 m，汽车绕z轴的转动惯量为4 607.4 kg·m2，前轮总侧偏刚度为-264 570 N/rad，后轮总侧偏刚度为-240 000 N/rad。仿真工况控制输入量见图3～5。

图3 双移线工况下车辆输出侧向加速度

图4 双移线工况下车辆输出纵向加速度

图5 双移线工况下车辆输出前轮转角

把车辆输出的控制量和观测量输入UKF算法模型中，对3个状态量进行实时估计。以Carsim软件中车辆输出的状态量结果作为虚拟试验值，将AUKF算法估计的状态量结果与虚拟试验值进行对比，验证AUKF算法的正确性。AUKF算法估计求解结果、UKF算法估计求解结果与虚拟试验值对比见图6～8。

图6 不同算法的横摆角速度估计值对比

图7 不同算法的质心侧偏角估计值对比

图8 不同算法的纵向速度估计值对比

由图6可知：采用UKF算法对横摆角速度进行估计时出现发散状态，表明在应对不同噪声时，UKF算法不能准确估计相应的状态参数；而AUKF算法对横摆角速度的估计值与虚拟试验值较接近，两者最大瞬态误差为0.5 (°)/s，相对误差仅5.101%，估计效果较理想。

由图7可知：采用UKF算法对质心侧偏角进行估计时出现发散状态；而AUKF算法对质心侧偏角的估计值与虚拟试验值接近，最大瞬态误差仅为0.04°，相对误差为3.633%。

由图8可知：采用UKF算法对纵向速度进行估计时出现发散状态；而AUKF算法对纵向速度的估计值与虚拟试验值接近，最大瞬态误差为1.875 km/h，相对误差仅为1.704%。

综上，采用AUKF算法对汽车状态参数进行估计的效果较好。

4 结语

采用自适应无迹卡尔曼滤波算法对汽车横摆角速度、质心侧偏角和纵向速度进行估计，结果表明该算法在车辆行驶环境中的噪声发生变化时仍可对相应状态参数进行估计，且估计精度较高。