基于Lyapunov稳定性的模块化多电平换流器反馈控制

莫跃，王健，刘明，杜丹

(1.中国南方电网有限责任公司超高压输电公司天生桥局，贵州 黔西南布依族苗族自治州562400；2.贵州大学电气工程学院，贵州 贵阳550025；)

模块化多电平换流器(modular multi-level converter, MMC)因其模块化、可扩展性、高效率、良好的谐波性能和故障阻断能力受到了广泛的关注[1-2]。近年来被广泛应用于中压大功率电机驱动系统、配电系统、高压直流输电网中[3-6]。然而，在应用MMC的控制系统中要保证输出电流和电压的质量，在保持电容电压平衡的同时最小化或抑制环流是有挑战的[7]。因此当MMC作为逆变器运行时，需要满足三个控制目标才能确保正常运行。第一，输出电流或电压必须控制在适当的幅度、频率和相位;第二，流经MMC各相的环流必须控制在一定值;第三，每个子模块(Sub Module,SM)的电容电压必须保持在参考电压。有学者已提出多种控制策略，其中，模型预测控制因其性能优点被广泛应用[8]。然而，随着SM数量的增加，其计算复杂度呈指数上升，因此，一些学者一直在减少计算负荷的方法上做了一些研究[9-11]。在文献[12]中，假定在电容电压完全相等的前提下，采用简单的线性控制器，通过基于反馈线性化的电流控制策略来调节输出电流和内部差分电流。相移脉宽调制(PS-PWM)[13]适用于SM数量比较少的情况，它具有良好的输出电压和电流质量，但开关频率高，占用大量硬件资源。与PS-PWM相比，最近电平控制(nearest level control,NLC)[14-15]简单，开关频率低，损耗小，随着SM数量的增加，NLC的输出质量优良。但当SM数量相对较少时，其输出电压和电流质量较差。参考文献[16-20]在一定的程度上改进了NLC的缺点。在参考文献[21]中，提出了在不对称运行条件下MMC的一般解析模型和改进的桥臂控制方法。

在鲁西站柔直功率模块故障诊断技术研究(CGYKJXM20180354)项目的支持下，针对上述控制方法的不足，研究并提出了一种能够优化多目标控制并实现动态跟踪的控制器。此外，控制系统的复杂性、动态响应、输出电流质量和换向不受SM数量的影响。

1 MMC的拓扑和数学模型

1.1 工作原理和拓扑结构

目前实际工程应用中，子模块通常采用半桥结构。上、下桥臂之间串联两个电抗器，阻感负载为星形联结，负载中性点与两电源中点相连，以保持负载中性点与电源中点电位一致且为零电位[22-23]。

每个桥臂上都串联了 N 个子模块，1 个桥臂电感 L 及等效桥臂电阻 R；而每个子模块中又由子模块电容C 和若干半导体开关器件构成，三相MMC的电路结构如图1所示，其单相由上臂和下臂组成。三相 MMC 基本拓扑结构包含 3个相单元和 6 个桥臂，且上、下桥臂相互对称，每个臂由N个子模块(SM)、一个电感和等效电阻串联组成，通过改变各桥臂投入的子模块数量即能起到调节 MMC 交流侧输出电压的作用[24]。

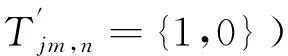
子模块由上IGBT S1、下IGBT S2，电容器C，以及续流二极管D1、D2构成。功率模块在接入桥臂时端电压为其内部电容器C的电容电压，旁路出桥臂时端电压为0。 MMC的功能是进行交流侧电压与直流侧电压的相互转换。MMC的交 /直流互换功能的实现依靠电压调制算法的控制。电压调制算法通过控制每个IGBT的导通和关断，按照一定的规律将桥臂的不同功率模块分时接入桥臂或者旁路出桥臂电路，使桥臂上接入的功率模块的串联电压呈现正弦波形，而在此过程中桥臂电流不断对功率模块电容器充电，维持电容电压的稳定。

1.2 MMC的数学模型

考虑图1中假设的直流侧中点，并使用基尔霍夫定律，可以获得j相中的MMC动态特性的数学方程以下:

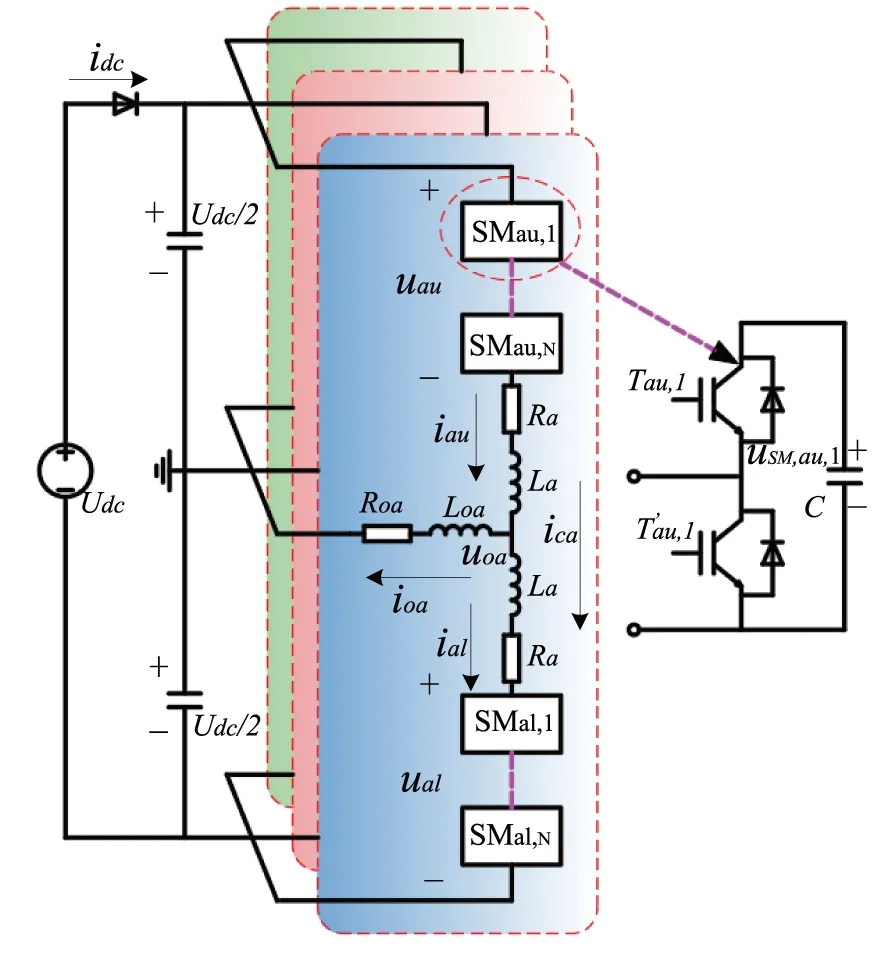
图1 一种三相MMC逆变器的结构及其SM[25]Fig.1 Structure of a three-phase MMC inverter and its SM[25]

(1)

(2)

ioj=iju-ijl

(3)

基于图1，根据文献[26]中所述，上下臂电流分别可表示如下:

(4)

其中icj是流经MMC第j相的环流，可通过以下公式获得:

(5)

通过将等式(1)减去等式(2)，并用等式(3)中的iju-ijl代替ioj，j相交流侧电流的动态特性如下:

(6)

类似地，通过将等式(1)和(2)相加，并用等式(5)中的iju+ijl代替icj，获得了j相中环流的动态特性，其表示如下:

(7)

设x1=ioj，x2=icj，u1=uju，u2=ujl，那么，j相的MMC的状态方程可以描述如下：

(8)

很明显，方程(8)是具有多个控制输入和干扰的耦合状态方程。特别重要的是，状态变量是周期性波动的正弦或余弦函数，这使得控制更加困难。经过理论分析与研究，建立MMC模型并利用MATLAB/SIMULINK进行仿真。

输出方程如下：

y=uoj=f(xoj)=R(t)xoj

(9)

(10)

2 基于李雅普诺夫稳定性的控制器设计

李雅普诺夫稳定性理论既适用于分析线性系统的稳定性，也适用于分析非线性系统、定常系统和时变系统的稳定性，是一种更为一般的稳定性分析方法。李雅普诺夫稳定性理论主要是指李雅普诺夫第二方法，又称为李雅普诺夫直接法。对非线性系统和时变系统，状态方程的求解往往很困难，因而李雅普诺夫直接法就展现出极大的优势。

本文就是借助李雅普诺夫稳定性理论，进行系统控制器的设计工作。在前一节中，我们已经得到了模块化多电平换流器的状态方程，参见方程(8)。那么接下来的任务就是如何设计控制变量u1和u2，使得x1的期望值为正弦，x2的期望值为常数。

2.1 控制器设计

本节基于所建立的状态模型，提出了一种系统的控制器设计方法，控制状态变量跟随期望值。将等式(8)改写如下:

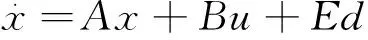
(11)

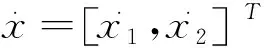
(12)

其中：

将(6)代入(9)得：

y=Cx+Du

(13)

其中y是 输出变量，

(14)

D=Loj[b11,-b11]

(15)

假设x的期望值是xd=[xd1，xd2]T,

e是x和xd之间的误差 ，那么

e=xd-x

(16)

在方程(16)的两边对时间求导

(17)

目标是要将误差收敛到零，即当t → ∞时，e→ 0。系统的控制算法分两步设计。

1)我们候选了一个Lyapunov函数V(e)，如下：

(18)

很明显，V(e)是正定的。通过对李雅普诺夫函数方程(18)求导得：

(19)

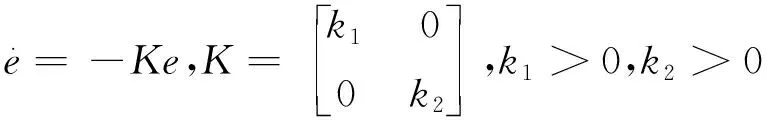
(20)

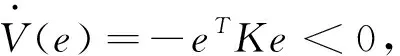
2)将式(16)和(17)带入式(20)，得：

(21)

再将式(11)带入(21)得：

(22)

整理式(22)求解u，得到如下控制律：

(23)

2.2 反馈跟踪性能

本节基于式(23)中考虑的控制器形式，在控制MMC动态性能之前验证状态变量跟踪性能。系统的框图如图2所示，系统的参数如表1所示。

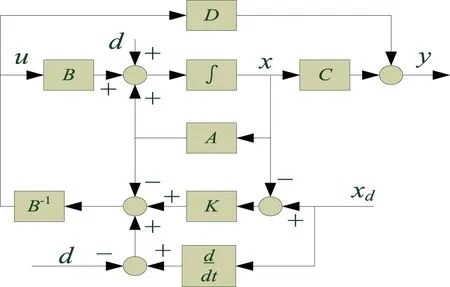
图2 系统反馈控制框图Fig.2 Control block diagram of system feedback

表1 系统参数Tab.1 System parameters

仿真框图如图2所示。在0.01s到0.012s的范围内，假设存在突变，这使得xd1振幅从500A变为250A，仿真结果如图3-图6所示。

如图3所示，x1能跟踪xd1，即使在xd1预期值出现突变时也能迅速做出反应，而且跟踪误差非常小，跟踪性能满足需求。在图4中，x2在很短的时间内实现对xd2的无差跟踪。这种响应速度大大满足了MMC的性能要求。因为x1和x2不耦合，xd1的突变不影响x2。

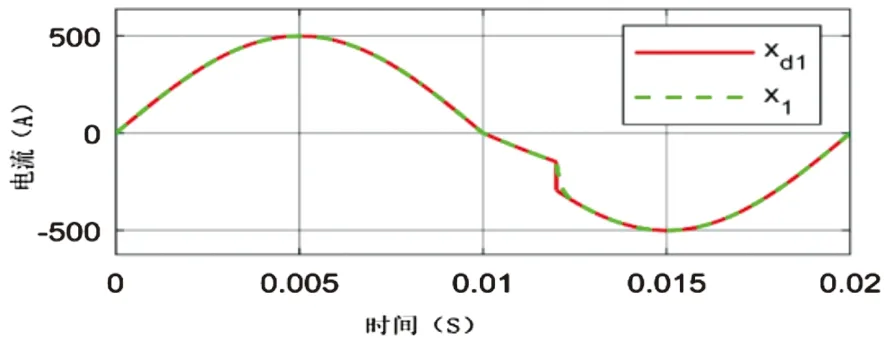
图3 输出电流x1跟踪xd1预期值的动态性能Fig.3 Dynamic performance of output current x1 tracking expected value xd1

图4 循环电流x2跟踪xd2预期值的动态性能Fig.4 Dynamic performance of circulating current x2tracking expected value xd2

在图5中，控制变量u1和u2的值从零变为负，然后迅速变为正，在0到近6000的范围内呈正弦曲线变化。它们的相角差是π，在0.01秒开始跳变，在0.012秒产生一个脉冲变化，然后迅速恢复正常。

图5 反馈控制矢量u1，u2的动态性能Fig.5 Dynamic performance of feedback control vector u1 and u2

输出电压y的波形如图6所示。开始时，波形由0V突变为750V，即一个SM的电容电压，然后根据正弦函数变化。仅在0.01s到0.012s期间，变化模式与图5中控制变量的变化模式相同。

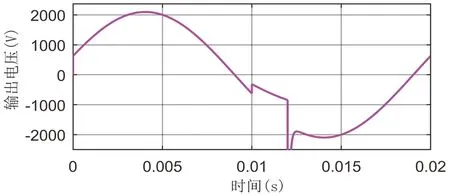
图6 输出电压y的动态响应Fig.6 Dynamic response of output voltage y

3 仿真结果

为了评估控制方法的性能，对每个臂包含4个和8个SM的三相MMC开关模型进行了仿真。MMC的控制框图如图7所示，MMC的参数如表2所示。在图7中，期望值xd，反馈增益K，以及状态变量x是反馈控制器的输入，反馈控制器如式(23)，进而获得最佳控制量u*。然后通过等式(24)计算j相上臂和下臂的插入的SM数njwnjl。子模块的投切功能利用文献[11]中的电压排序算法计算实现，以平衡MMC所有模块的电容电压uSM,jm,n。由于控制系统的最佳控制u，因此不受子模块数量的影响。

表2 MMC的主要电气参数Tab.2 Main electrical parameters of MMC

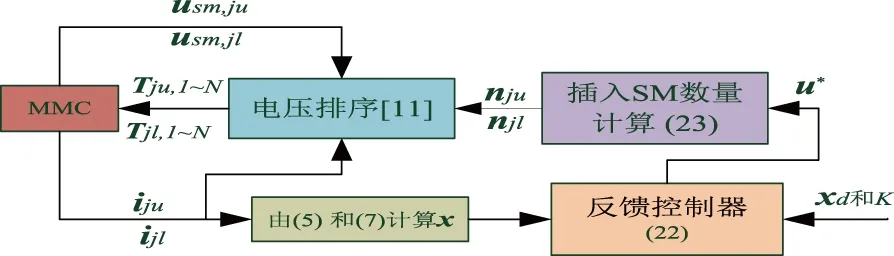
图7 MMC控制框图Fig.7 Control block diagram of MMC

插入MMC的SM的最佳数量如下:

(24)

其中njwnjl分别是插入MMC上臂和下臂的子模块数量，uC是子模块的标称电容电压，如下所示：

(25)

在式(23)中得到的u是一个连续函数，在式(24)之后，它被MMC的SM结构离散化。这就是电力电子电路的特点，一个连续和离散的混合系统。

假设MMC的三相的电路结构相同，并且上臂和下臂具有相同的电路拓扑结构。为了便于理解，在下面的研究中，仅以a相为例进行分析。其他两相的分析方法相同。

本文对四种情况进行了比较和分析，如表3所示。

表3 仿真情况分类Tab.3 Classification of simulation situations

3.1 输出电流/电压性能比较

四种情况下交流侧输出电流和电压的仿真结果分别如图8所示。为了进一步验证所提出控制方法的优点，图9和图10给出了输出环流和电容电压的波形。

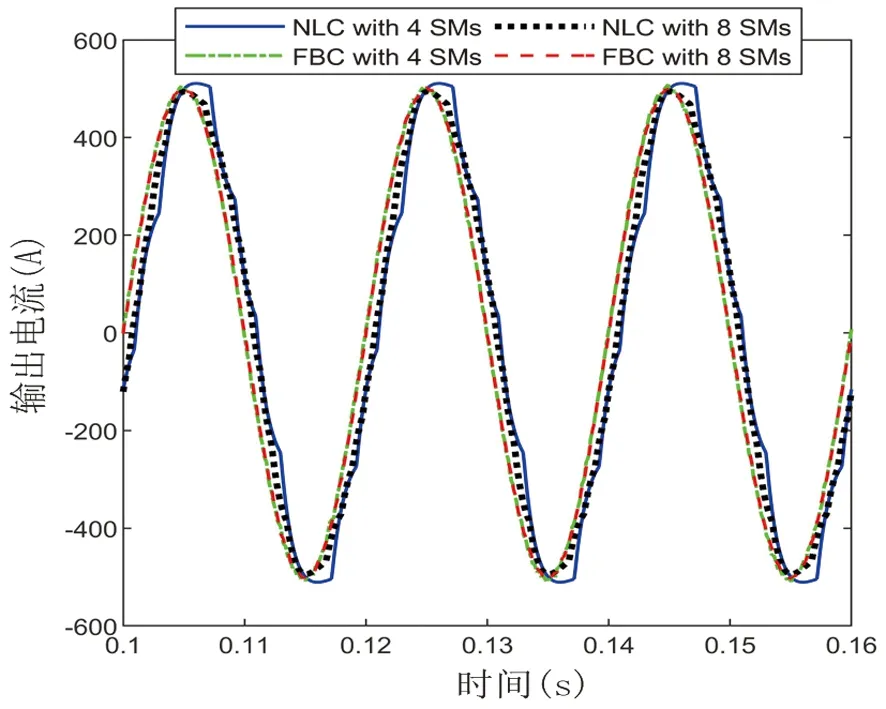
(a)4种条件下a相输出电流(ioa)的波形分析(a)Waveform analysis of a-phase output current (ioa) under 4 conditions

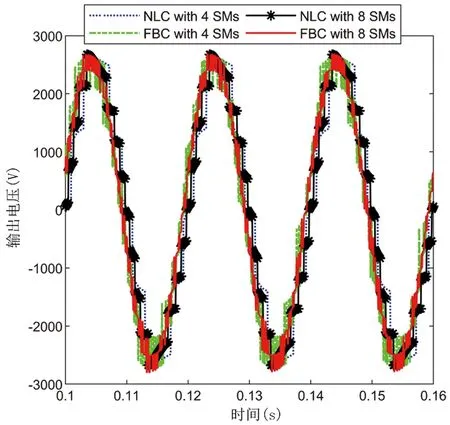
(b)4种条件下a相输出电流(uoa)的波形分析(b)Waveform analysis of a-phase output voltage (uoa) in the case of 4 conditions图8 四种情况下a相输出电流和电压的波形Fig.8 Waveform of a-phase output current and voltage in four conditions

在图8(a)中，每臂4个SM的最近电平调制控制与每臂8个SM的最近电平调制控制得到的电流波形完全一致，近似于正弦波形。每臂4个SM的反馈控制跟踪效果最差，每臂8个SM的反馈控制效果次之。与每臂4个SM的反馈控制相比，每臂8个SM的反馈控制得到的波形有了改善。基于该控制方法，输出电流的质量不受SM数目的影响。

在图8(b)中，每臂8个SM的反馈控制得到的电压波形最好，每臂4个SM的反馈控制次之，每臂8个SM的反馈控制效果再次之，每臂4个SM的反馈控制最差。另外，从图8(a)和图8(b)可以看出，采用最近电平调制控制方法的波形具有一定的滞后性。

3.2 输出电流性能比较

图9展示了四种情况下a相环流的仿真结果。每臂8个SM的反馈控制抑制环流效果最好，每臂4个SM的反馈控制次之，每臂8个SM的最近电平调制控制效果最差。xd2的期望值是120A。所提出的控制策略明显能有效地抑制环流的波动。这使得输出环流在120A的期望值附近波动，误差很小。

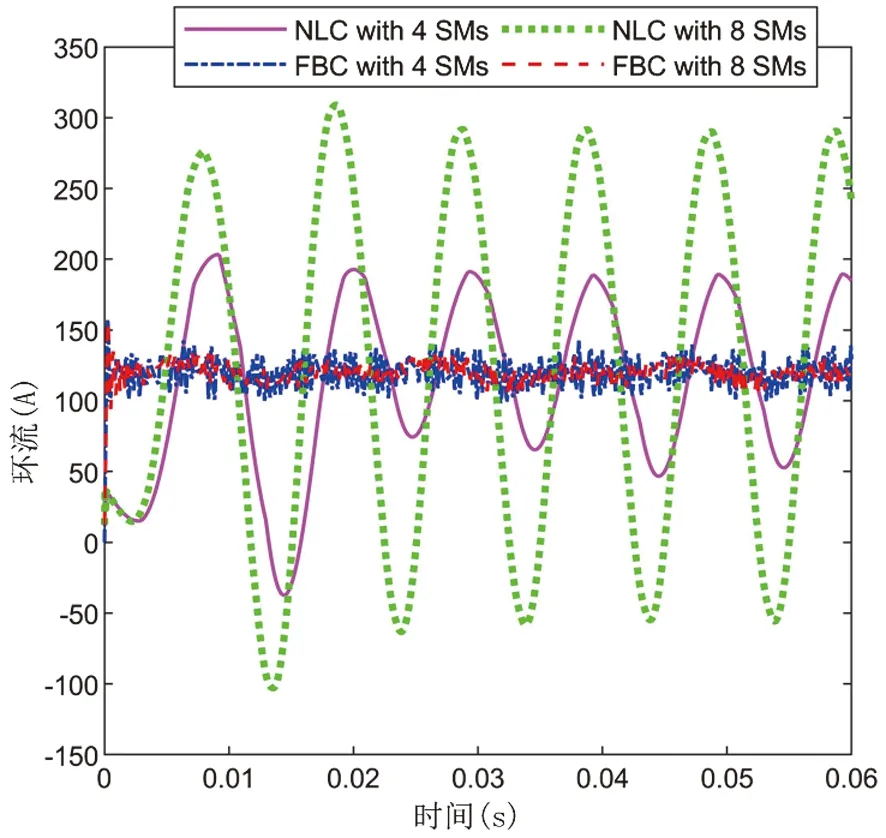
图9 四种情况下a相环流(ica)波形Fig.9 A-phase circulating current (ica) waveform in four cases

最近电平调制控制策略对环流的抑制效果并不理想，而且随着SM数的增加，抑制环流的效果越来越差。

3.3 电容电压分析

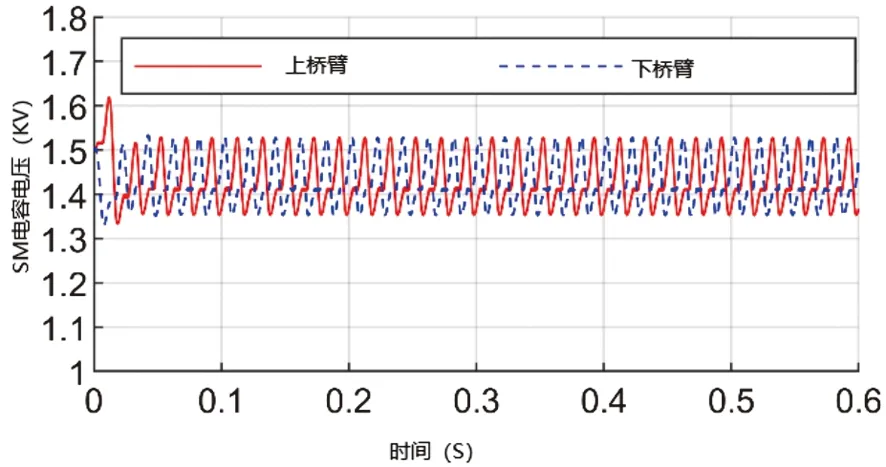
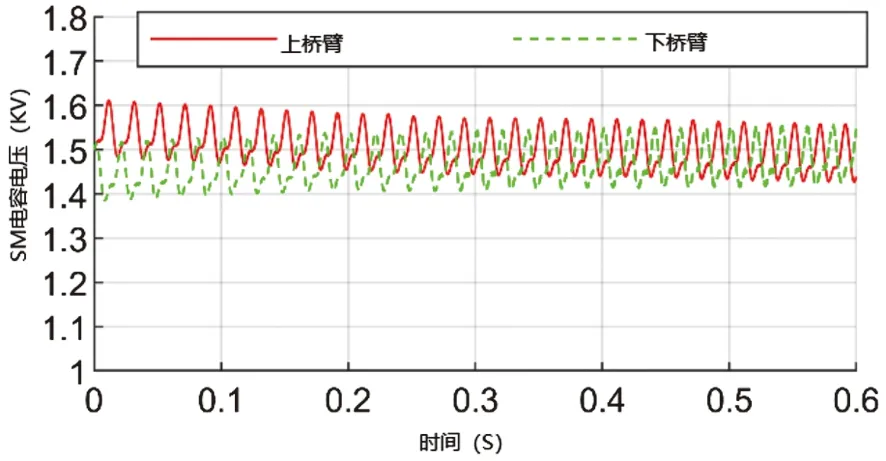
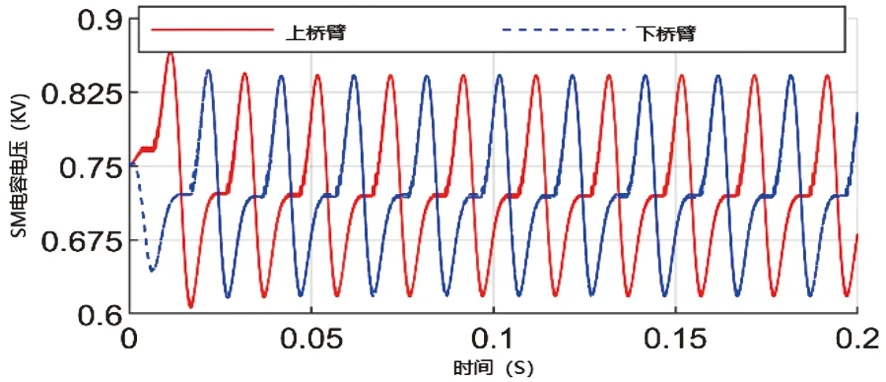
a相电容电压的动态响应如图10所示。图10(a)和图10(c)对应的电容器标称电压为1500V，图10(b)和图10(d)对应的电容器标称电压为750V。考虑到数据的稳定性，在下一次分析中，数据采集在时区[0.03，0.06]之间。

(a)每臂4个SM的最近电平调制控制(a)NLC with 4 SMs

(c)每臂4个SM的反馈控制(c)FBC with 4 SMs

(b)每臂8个SM的最近电平调制控制(b)NLC with 8 SMs

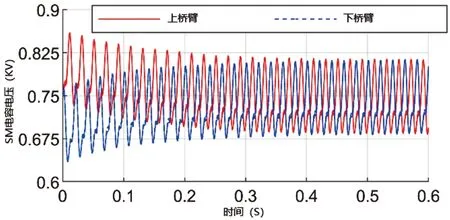
(d)每臂8个SM的反馈控制(d)FBC with 8 SMs图10 4种情况下a相上、下臂的SM电压Fig.10 SM voltages of the upper and lower arms of phase a under 4 conditions

在图10(c)中，上臂SM电容电压波动范围为1426.2V～1570.9V，下臂为1409.6V～1553.5V，与标称电压相比，上臂的波动范围为-73.8V～70.9V，波动率为-4.92%～4.73%(下臂为-91.4V～53.5V，-6.03%～3.57%)。上臂平均值1489.9V，标准差41.68(下臂平均值1472.2V，标准差41.77)。所有SM电容器的电压数据均采用相同的方法获得，如表4所示。

综上所述，综合图10和表4得出以下结论：

表4 四种仿真情况下SM电容电压的数据分析Tab.4 Data analysis of SM capacitor voltage in four simulation situations

(1)采用反馈控制策略，电容电压的标准差接近，在4种情况下是最小的，并随时间的增加而逐渐稳定；

(2)每种情况下，当采用反馈控制策略时，上下臂电容电压不同，采用最近电平调制控制策略时基本相等；

(3)采用反馈控制策略时，电容电压值更接近标称值；

(4)随着SM数的增加，电容电压的波动范围增大，如每臂8个SM的MMC分别采用反馈控制策略和最近电平调制控制策略，但采用反馈控制策略时电压波动幅度较小，电压波动幅度也与电容电压标称值的降低有关。

续表

仿真情况类别上/下臂标称(初始)值/V平均值/V标准偏差/V最大值/V最小值/V波动率/%NLC with 8 SMs上臂750723.163.13842.59617.59-17.66～12.35下臂750723.562.96842.675617.49-17.67～12.36FBC with 4 SMs上臂15001489.941.681570.91426.2-4.92～4.73下臂15001472.241.771553.51409.6-6.03～3.57FBC with 8 SMs上臂750745.5241.87836.42682.62-8.98～11.52下臂750732.7741.88812.99662.48-11.67～8.40

4 反馈增益对电流谐波的影响

上一节的仿真分析中，直接采用了反馈增益k1=12000，k2=15575。接下来将进一步分析在不同反馈增益条件下，其对电流谐波的影响。为了充分研究，对于9电平(每臂8个SM)做了25次实验，k1从1550到12000变化，k2从600到20000变化，其相应参数见表5所示。从数据来看，随着增益的逐渐增大，电流THD(总谐波失真)逐渐减小，到k1=12000，k2=15575时，THD=0.52达到最小值，而之后THD缓慢增加。鉴于控制器不希望增益过大，因此进行了25组数据后就结束了。同理也对5电平(每臂4个SM)进行了研究，其结果趋势和9电平相同，也是在k1=12000，k2=15575时，THD=1.03达到最小值。

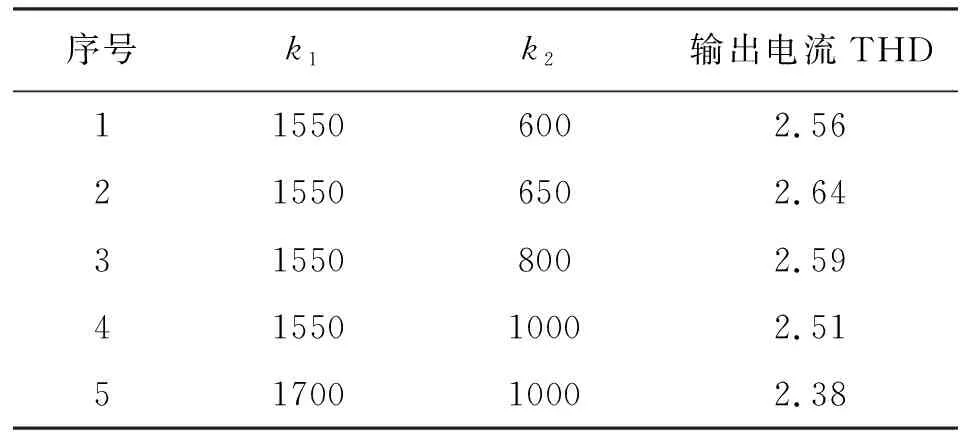
表5 增益对电流谐波的影响Tab.5 Influence of gain on current harmonics

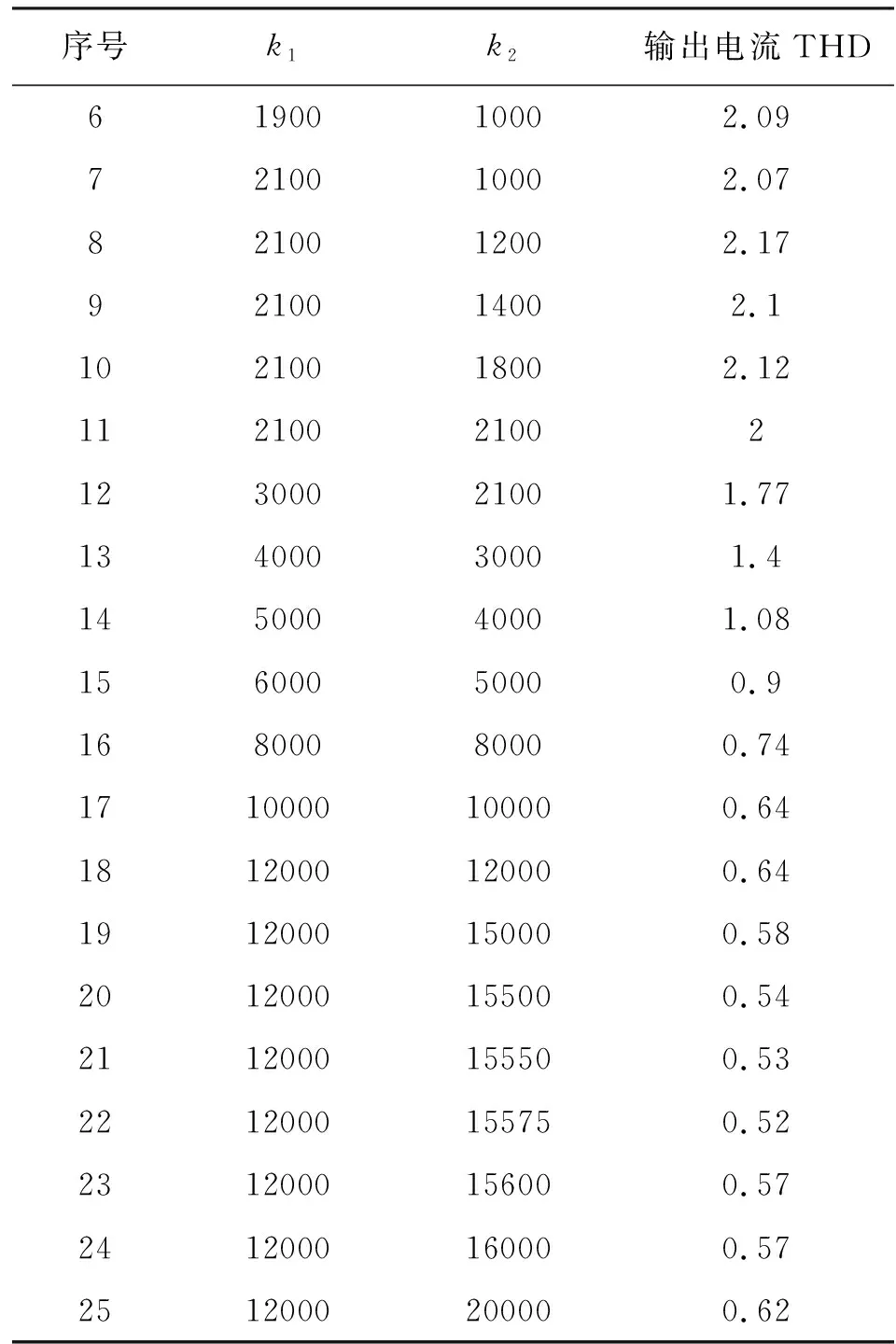
续表

因此，本文的研究采用反馈增益k1=12000，k2=15550。此时输出电流的THD是最小的。此外还可以看到9电平的THD比5电平的THD小一半。也即是，在桥臂子模块(SM)数量较少时，桥臂子模块的数量与输出电流的THD成一定的比例关系。当然这个结论并不代表桥臂子模块(SM)数量较大时适用。

5 结论

本文提出了一种基于Lyapunov稳定性的控制器设计方法。为了描述MMC交流侧电流和环流的动态特性，建立了模块化多电平的数学模型。与传统的控制模型不同，该模型不需要坐标变换。上(下)臂的电压用作控制输入，以调整插入上(下)臂的SM数量。然后，根据输出电流和环流反馈，对上下臂电压进行校正。即根据输出电流和环流与它们各自的期望值之间的误差来校正上(下)臂的电压。仿真结果验证了该方法的有效性。与传统的最近电平调制控制控制器相比，所提出的反馈控制控制器可用于包含不同SM数目的MMC中，其输出电流和环流具有良好的动态性能和较低的谐波分量。特别地，所提出的反馈控制控制器还具有传统最近电平调制控制控制器的优点，例如便于理解和计算，适合在时域中使用。