网络化遥操作系统的全状态时变约束控制研究
杨亚娜,代 特
(燕山大学 电气工程学院,河北 秦皇岛 066004)
0 引言
典型网络化遥操作系统主要由操作者、主机器人、网络信息传输通道、从机器人和从端的外界工作环境五部分组成[1]。其工作模式可大致描述为:操作者操作主机器人,并将主机器人的位置、速度等信息通过网络等传输媒介传输给远端从机器人,从机器人根据接收到的主机器人信号在特定环境下模拟主机器人的行为来配合操作者完成各项工作。同时,从机器人将自己的位置、速度、力等信息通过网络传输通道反馈给操作者,便于操作者根据从机器人的运动状态做出正确的决策[2-3]。遥操作系统作为能最大限度发挥人类和机械系统各自优势的远程操作系统,目前已被广泛应用于核事故救援、空间探测、海底作业和远程医疗以及农业等多个领域[4-7]。
随着遥操作系统使用范围的不断扩大,对遥操作系统控制性能的要求日益提高。遥操作系统控制器的设计需同时满足多种性能需求:1)通信时延下闭环遥操作系统的稳定性;2)良好的主-从机器人同步精度;3)较快的系统瞬态响应速度等。由于主-从机器人之间通过网络相连,因此不可避免地存在通信时延问题[8]。另外,遥操作系统作为典型的非线性系统,在实际中存在不同程度的模型未知、参数不确定以及未知外界干扰等问题。遥操作系统在实际工作中,由于工作环境的限制、操作的安全性以及性能提高的考虑,系统状态往往受到不同程度的约束。正是因为主-从通信时延、系统不确定性和系统状态约束的存在,迫切需要针对网络化遥操作系统设计全状态约束控制策略以保证主-从系统高精、快速同步的基础上,保证系统状态始终处于所约束范围以内。
近年来,针对单机器人以及非线性系统的状态约束控制问题,现有文献进行了深入的研究。许多有效的控制设计方法,包括模型预测,参考调节器和函数集合不变性概念被提出。除此之外,基于障碍Lyapunov方程(Barrier Lyapunov Function, BLF)的控制器设计方法取得了大量的研究成果。该方法通过设计新的带有约束的Lyapunov方程,并设计有效的控制器,使得Lyapunov方程始终有界,即所选取的约束函数有界,从而确保受限状态始终处于约束范围以内[9]。基于该方法,文献[10]针对严格反馈非线性系统提出了一种针对输出约束的控制器设计方法,通过选取对称时变BLF来确保系统输出满足约束条件。进而文献[11]针对一类非线性系统考虑系统的部分状态约束问题,提出了一种新的基于BLF的控制方案。文献[12]针对一类具有输入饱和、状态约束、匹配参数不确定性和输入扰动的多输入多输出系统,提出了一种双环控制方法。文献[13]针对一类具有全状态约束的非线性纯反馈系统设计了自适应控制方案。然而,在上述文献中,大多只考虑系统的输出约束或者带有恒定约束条件的状态约束问题。然而,由于实际工作环境的复杂多变以及控制目标的时变性,非对称时变状态约束问题更具实际研究意义。另外,虽然现有针对非线性系统状态约束问题取得了一定的研究成果,但上述控制方法很难直接应用于带有信号传输时延的网络化遥操作系统。
在遥操作系统的实际应用中,主-从机器人之间的通信传输时延特别是时变的传输时延,给控制器设计带了巨大的挑战[14-17]。文献[18]针对带有定常时延的遥操作系统,考虑机器人位置约束问题,设计自适应控制器,保证了主从机器人的快速同步性能。进而,文献[19]针对带有定常时延、输入饱和、多状态约束下的双边遥操作系统的同步控制问题进行了深入研究,通过设计神经网络控制策略保证了闭环遥操作系统的稳定性。然而,实际中主-从端通信时延大多具有非对称时变特性。
针对以上存在的问题,本文拟针对带有非对称时变约束、系统不确定、未知外界干扰的网络化遥操作系统在多状态约束下的控制问题展开研究,通过设计新的自适应神经网络控制策略,保证闭环遥操作系统稳定的同时,使得系统状态始终处于受限的范围以内。本文的主要贡献点可归纳如下:
1) 针对带有模型和参数不确定的网络化遥操作系统在时变非对称全状态约束下的同步控制问题,通过设计新的自适应控制策略保证系统具有良好的暂稳态性能。
2) 针对主-从机器人之间存在的不对称时变通信时延,本文创新性地利用非线性观测器在线估计并补偿时延的影响,从而避免控制器的设计依赖于时延导数信息,在提高系统跟踪精度的基础上,增强了控制器的实用性。
3) 径向基神经网络(Radial Basis Function Neural Networks,RBFNN)与障碍Lyapunov函数的结合放松了神经网络控制中要求输入信号均保持在一个紧集合这一假设条件,且通过设计简化的调整机制,减少计算量,缩短神经网络计算时间。
4) 利用Nussbaum增益,很好地处理了不确定输入矩阵对系统稳定性的影响,实现更高精度的同步控制。
1 预备知识
1.1 遥操作系统模型描述
考虑两个具有n-关节机械臂组成的主-从非线性遥操作系统动力学模型:

(1)
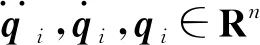
上述非线性主-从机器人系统存在如下重要属性:
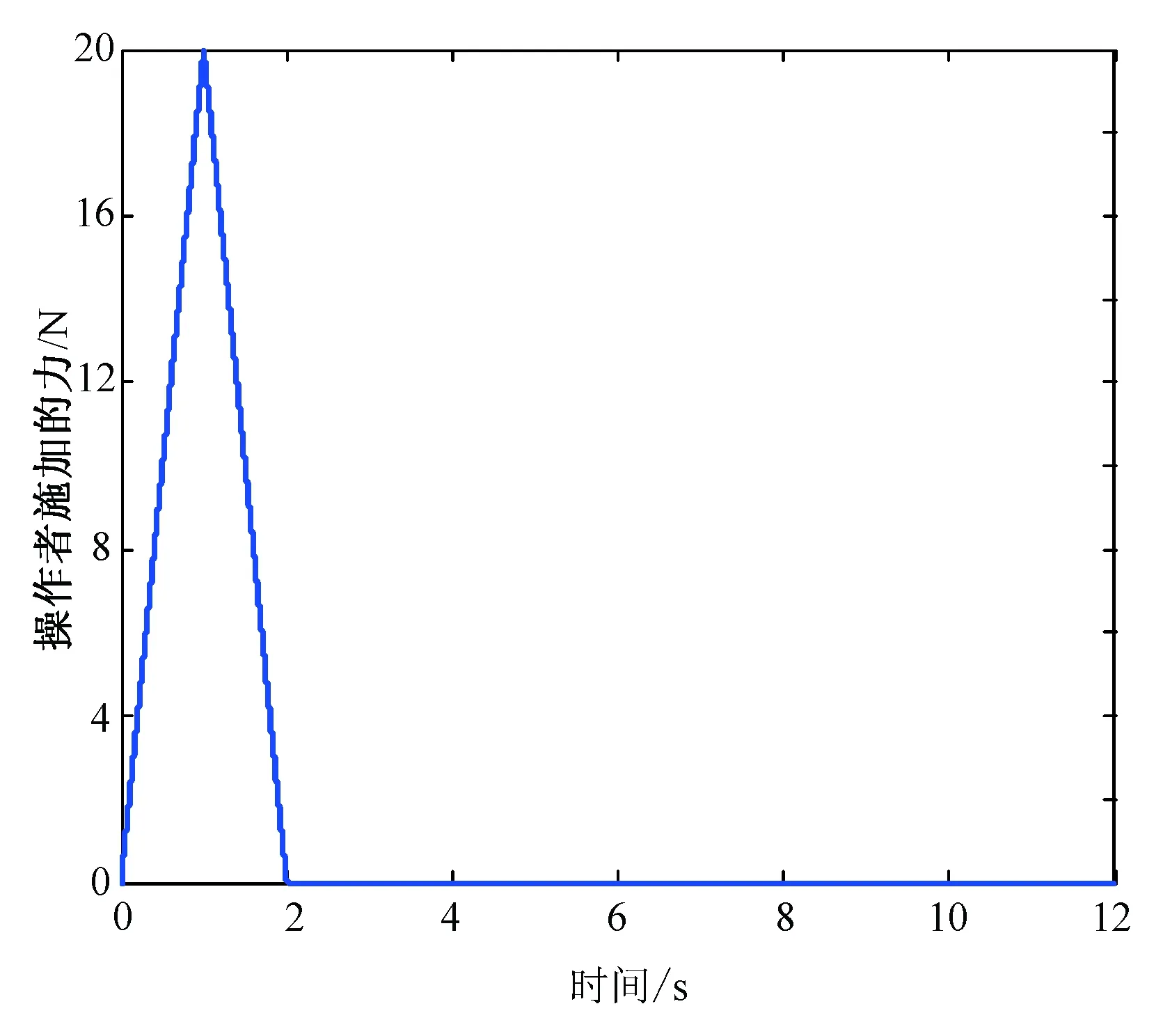
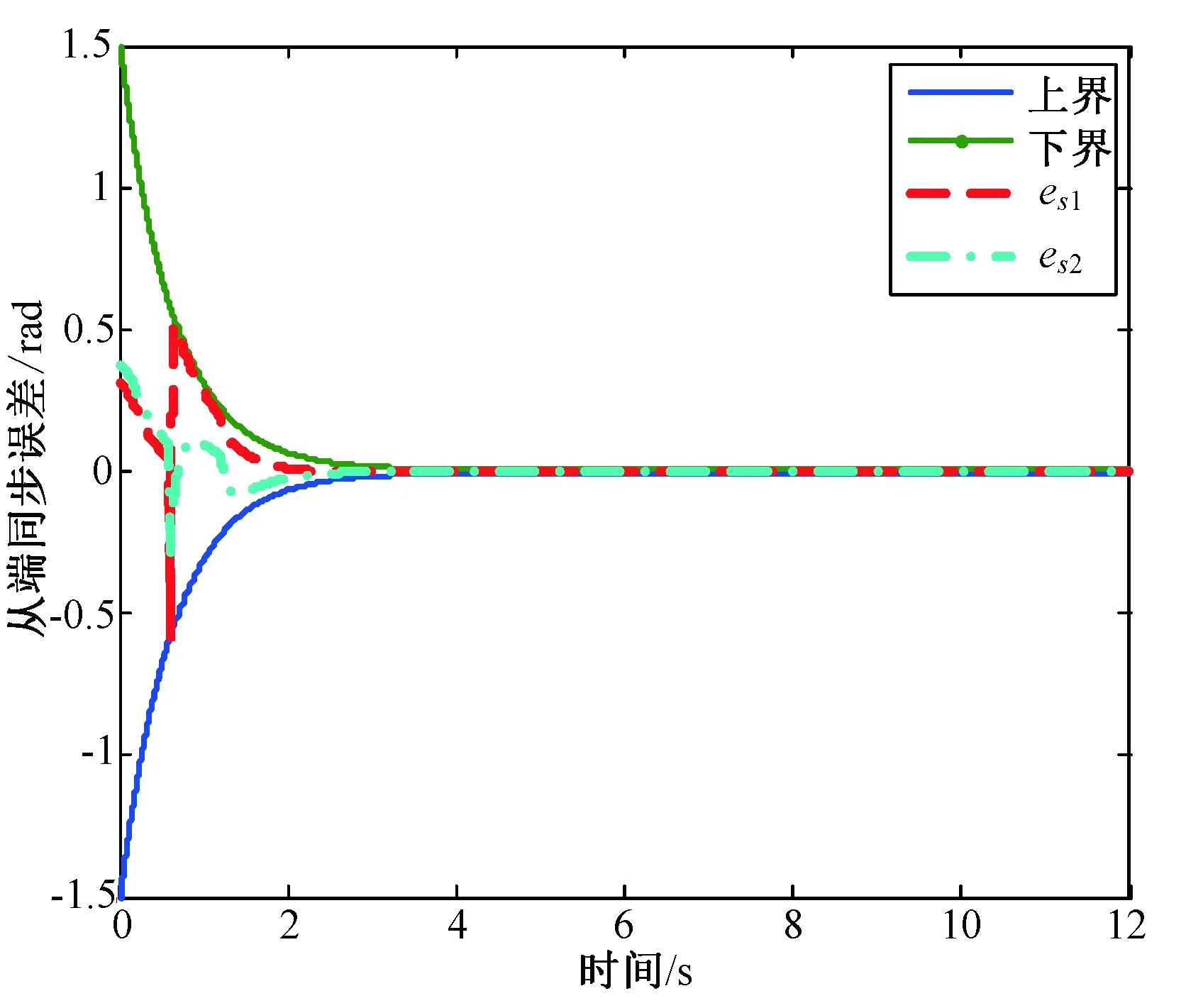
属性1[1]:Mi(qi)为对称正定惯性矩阵,存在正常数mi1和mi2使不等式mi1I (2) (3) 首先,考虑当系统状态满足|x| (4) 引理1[9]:对于任意正常数Nb以及向量∀x∈Rm,在区间‖x‖ (5) 定义2[20]:定义任意连续函数N(ζ):R→R当其满足 (6) 时,则称其为Nussbaum类型函数。 引理2[21]:V(·)和ζ(·)为定义在[0,tf)上的光滑函数,∀t∈[0,tf)使得V(·)≥0。N(ζ)为光滑的Nussbaum类型函数,且为偶函数,若对任意的t∈[0,tf),可使如下不等式成立: (7) 其中,c0>0,c1>0为常数,η为时变参数。 引理3[22]:Γ为m×m的对称矩阵且x∈Rm为非零向量,定义ρ=(xTΓx/xTx),则Γ分别在[ρ,∞)和(-∞,ρ]上至少存在一个特征值。 (8) xTRix=βi(t)xTx, (9) 为处理未知函数βi(t),本文采用了形如式(5)的Nussbaum增益函数N(ζ)=eζ2cosζ。 神经网络因其强大的函数逼近能力,学习能力以及很好的容错力,在非线性系统控制中得到了广泛的应用。而径向基神经网络(RBFNN)因其简单、线性化参数结构的特点得到迅速发展。一个未知非线性函数f(Z):Rl→Rm1在集合ΩZ∈Rl上可通过径向基神经网络在线逼近[22],可描述为 f(Z)=WTJ(Z)+δZ(Z), (10) 其中,Z∈ΩZ⊂Rl为神经网络输入,W∈Rp1×m1为径向基神经网络(RBFNN)的最优权重矢量,p1>1为神经元个数,δZ∈Rm1表示近似误差,J(Z)=[φ1(Z),…,φp1(Z)]T∈Rp1为已知的光滑基函数向量,φi(Z)(i=1,2,…,p1)通常选为高斯函数: (11) 为保证非对称时变时滞下不确定闭环遥操作系统在全状态时变约束下的稳定运行,首先通过设计新的非线性观测器,基于带有时变时延的位置信息获得相应的速度和加速度信息;其次,针对实际约束条件选取合适的BLF,并设计新的自适应神经网络控制器;最后,通过证明所选取BLF的有界性,从而可得闭环遥操作系统稳定,且系统状态始终处于预设的范围以内的结论。 首先,定义主-从位置同步误差: (12) 其中,Tm(t)表示信号由主端传递到从端的时间延迟,Ts(t)表示信号由远处的从端传递到主端的时间延迟。进而定义 (13) 其中,αm1,αs1为虚拟控制器,虚拟控制器的设计将在后续给出。 进一步,关节速度同步误差给出如下: (14) 显然,Dm和Ds中含有时变时延导数信息。实际中,时延导数信息很难精确测得。针对该问题,本文设计新的非线性观测器,在线估计Dm和Ds,并在控制器中进行补偿[25]。 针对系统(13)设计如下非线性观测器: (15) (16) 结合式(14)、(15)和(16),可得观测器观测误差方程为 (17) (18) 引理4的具体证明可参考文献[26]。 注2:本文所设计的非线性观测器可实现对网络传输时延导数所产生的不确定项进行快速、精确估计,进而可在控制器设计中进行消除。在保证时变时延下闭环遥操作系统稳定性的同时,可以提高主-从机器人之间的同步精度。 遥操作系统中,主端机器人一般由操作者操控,而从机器人通常位于远端完成各种复杂任务,考虑到从机器人在实际应用中可能存在的环境约束,同时出于安全考虑,人为限定从机器人的工作范围。由于从端任务的不断改变,不对称时变约束更加符合实际应用需求,所以本文针对从端机器人考虑了时变非对称约束下的全状态约束控制器设计问题。下面给出控制器的设计过程及系统稳定性的证明。 第一步:选取BLF如下: (19) 其中,zs1j表示向量zs1的第j个变量,且该定义同样适用于其他变量,Nbb1(t),Nab1(t)为非对称时变约束值,定义集合:Ωzs1:{zs1j|-Nab1(t)<|zs1j| 对V1求导并结合式(12)可得 (20) 虚拟控制器αm1,αs1设计如下: (21) 将式(21)代入(20)可得 第二步:选取新的BLF: (22) 其中,Nbb2(t),Nab2(t)表示时变非对称约束,定义集合:Ωzs2:{zs2j|-Nab2(t)<|zs2j| 同样对V2进行求导: (23) (24) 结合杨氏不等式可以得如下不等式: 由此可得 利用上述不等式对式(24)进行放缩: 根据方程(6)定义的Nussbaum增益函数,设计自适应神经控制方案如下: (25) (26) (27) 定理1考虑双边遥操作系统(1),采用自适应神经网络控制器(24)以及自适应调节律(25)和(26),当初始条件满足:zs1(0)∈Ωs1:={zs1∈Rn:Nab1<|zs1j| -Nab1<|zs1j| 证明:选取Lyapunov函数如下: (28) (29) (30) 结合引理1得如下不等式: 将上述不等式带入式(30): (31) 其中,μ=min{2km1,2cm1,2ks1,2cs1,κm,κs}, 对式(31)两边进行积分: 此外,从机器人状态一直处于约束界内,即 -Nab1<|zs1j| 证毕。 为验证本文所提出的自适应神经网络全状态约束控制器的有效性,仿真中考虑了由两个相同的2自由度机械臂组成遥操作系统,仿真中2自由度机器人系统的模型定义为 g1(q)=g(m2l2cos(q1+q2)+(m1+m2)l1cos(q1)), 操作者施加到主机器人的力如图1所示。在操作者施加力的作用下主机器人开始移动,并将自己的位置和速度信息通过网络传输通道传输至从机器人端。进而,从机器人在控制器作用下跟随主机器人运动。 图1 操作者施加到主机器人的力Fig.1 Force inserted by the operator to the master 主-从机器人之间的位置同步误差如图2所示。从图2可以看出,在本文设计的自适应神经网络全状态约束控制器下,当操作者施加的力为零后,主、从同步误差将在1.5 s收敛至零点。且主-从位置同步误差始终处于被约束的时变约束范围内。因此从图2可以看出,操作者可以通过控制主机器人的运动使得从机器人跟随主机器人运动而完成特定的作业。由于主机器人位置有界,且主-从机器人位置误差有界,可得从机器人位置有界的结论,因此可知从机器人位置满足约束条件。 图2 从端关节同步误差Fig.2 Synchronization errors at slave side 进而,从机器人的关节速度约束变量示意图给出如图3所示。从图3可以看出,在本文设计的控制器下,当操作者施加力为零时,从机器人速度快速趋于零点,且主-从机器人速度误差始终处于所约束的范围内。由于主机器人在操作者的控制下速度信号始终有界,且主-从速度误差有界,因此可得从机器人速度有界的结论。最终表明从机器人速度始终处于受限的范围以内。 图3 从机器人速度受限信号Fig.3 Constrained velocity signal at slave side 以上仿真结果,充分验证了本文所设计控制器在系统存在模型和参数不确定、未知外界干扰、非对称时变时延以及全状态时变约束下控制的有效性。 本文针对全状态时变约束条件下,带有系统不确定性和非对称时变时延的遥操作系统的同步控制问题进行了研究。创新性地将全状态时变约束问题转化为系统的稳定性问题,提高了主-从系统同步精度的同时,避免了因系统状态突然增大导致的碰撞问题。通过引入新的非线性观测器保证了闭环遥操作系统在非对称时变时延下的稳定性。进而,引入径向基神经网络在线估计系统动态不确定性,并应用Nussbaum增益处理系统输入矩阵不确定的问题。通过构造新的障碍Lyapunov函数证明了主-从系统的稳定性和同步性能。最后,仿真结果验证了本文设计方案的有效性。
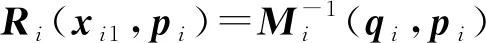
1.2 障碍Lyapunov函数
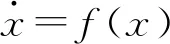


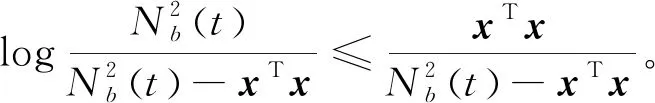
1.3 Nussbaum增益
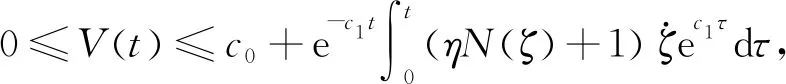


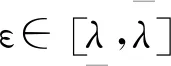

1.4 径向基神经网络


2 控制器设计及稳定性分析
2.1 非线性观测器设计



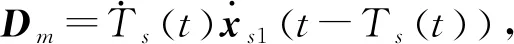
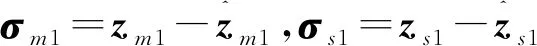
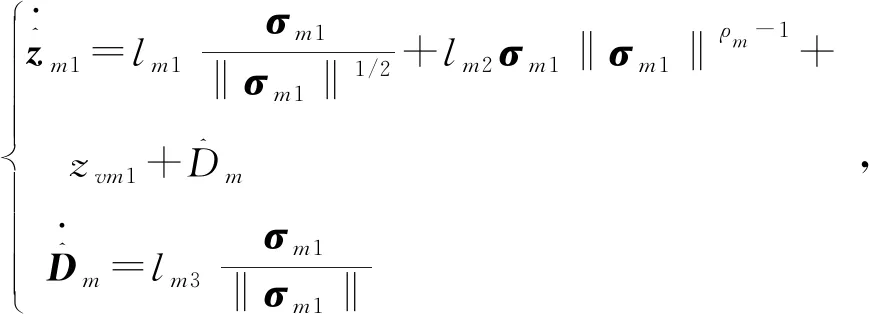


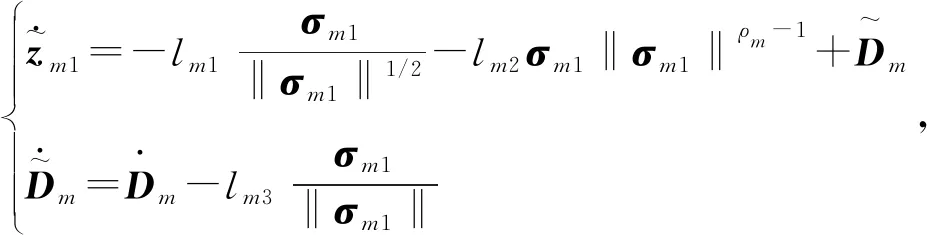


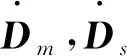
2.2 全状态约束控制器的设计
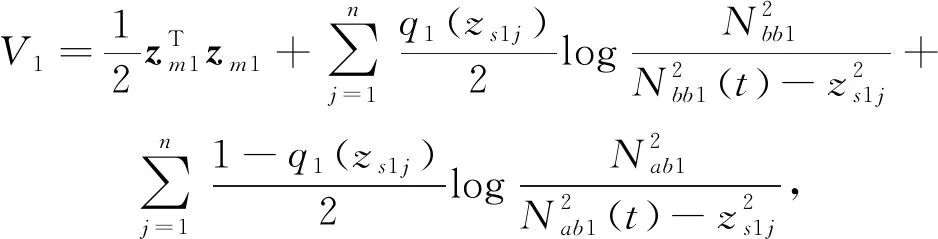








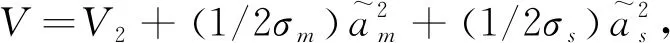
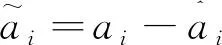


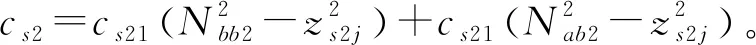
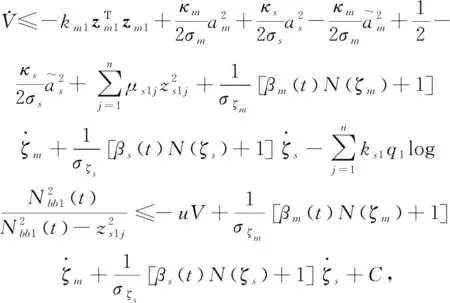
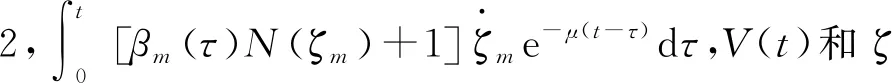
3 仿真实例
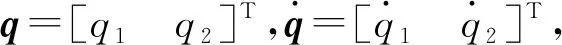
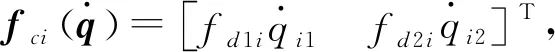


4 结论

