融合虚拟机分簇与休眠机制的MEC任务卸载策略

王 颖，李 伟，陈梦盼，陈 利，金顺福,*

(1. 燕山大学 信息科学与工程学院，河北 秦皇岛 066004；2. 燕山大学 里仁学院，河北 秦皇岛 066004)

0 引言

随着科技的进步，大量能源密集型和计算密集型的应用程序应运而生[1]。然而，每个移动设备本地的计算资源和存储容量等有限，传统的云计算[2]又因高延时及低安全性等缺陷不能满足网络用户需求，移动边缘计算(Mobile edge computing，MEC)[3]的概念应运而生。面向MEC的任务卸载策略成为该领域关注的焦点。

提高应用程序的响应性能是保证网络用户服务质量的重要因素，部分文献中的任务卸载策略侧重于减少任务平均延时。Tang等人[4]提出了一种基于MEC的充放电联网系统，利用一种求解整数变量的启发式算法，分析各变量的凸性，以实现充电站等待时间的最小化。Yu等人[5]提出了一种缓存增强的计算卸载问题，基于协作调用图平衡卸载与缓存之间的关系，最小化移动终端的执行延时。Zhang等人[6]提出了一种分层卸载框架，采用斯塔克尔伯格博弈方法设计了一种多层卸载方案，使用迭代分布算法得到了最优的卸载策略，在保证计算延时的同时最大化收益。这些任务卸载策略的研究忽略了MEC中的能耗水平。

立足于绿色MEC的建立，部分文献中的任务卸载策略研究专注于减少系统能量消耗的技术。Xu等人[7]提出了一种用于eNodeB缓存的能量消耗模型，使用线性规划方法分析系统能耗水平，采用拉格朗日对偶分解技术最小化系统能量消耗。Gu等人[8]研究了虚拟机迁移，任务分配及能量调度问题，提出了一种离散时间槽调度优化模型，利用一种基于松弛的启发式算法，实现能量消耗的最小化。Mehamel等人[9]提出了一种高效能的边缘设备模糊缓存技术，利用现场可编程逻辑门阵列实现边缘缓存的模糊决策，以降低边缘缓存的能耗。这些研究忽略了响应性能对网络用户服务质量的影响。

本文基于多用户应用环境，综合考虑响应性能及节能水平，研究MEC任务卸载策略。系统中主模块持续活跃以提高网络用户的响应速度，备用模块中引入休眠机制以实现节能的目的。根据主模块及备用模块中的任务数量以及备用模块虚拟机的状态，使用拟生灭过程与矩阵几何解方法进行稳态解析。构建系统成本函数，改进鸽群算法，研究任务卸载策略的参数优化问题。

1 MEC任务卸载策略及系统模型

1.1 MEC任务卸载策略

随着计算机技术与通信技术的不断发展，移动设备的计算能力不断增强，但依然存在短时间内消耗大量资源的问题。云计算因传输距离远等问题，又会造成不可预测的延时[10]。兼顾响应性能及节能水平，融合虚拟机分簇与休眠机制，面向MEC服务器提出一种任务卸载策略，如图1所示。

图1 MEC系统任务卸载Fig.1 Task offloading in MEC system

1) 考虑移动设备在计算性能和资源存储等方面存在的不足，一定比例的任务在移动设备本地执行，而剩余的任务则可以卸载到MEC服务器上接受服务。采用虚拟机分簇技术，在MEC服务器中设置时刻保持活跃的主模块及在活跃状态与休眠状态之间自适应切换的备用模块。

2) 主模块虚拟机持续活跃，可以随时为到达系统的任务提供服务。卸载到MEC服务器上的任务，首选进入缓存容量有限的主模块。若主模块中存在空闲虚拟机，新到达的任务立即接受服务。否则，将尝试进入缓存队列中排队等待。若主模块中的可用容量为零，新到达的任务将进入缓存容量无限的备用模块中。

3) 备用模块中的虚拟机在活跃状态与休眠状态之间自适应切换。当备用模块虚拟机中的所有任务服务完毕后，若缓存队列中没有等待的任务，立即启动休眠定时器，全部虚拟机同时进入第一个休眠期。一旦备用模块虚拟机处于休眠状态，新到达的任务只能进入缓存队列中等待。一个休眠期结束后，若缓存队列中没有等待的任务，则全部备用模块虚拟机同时开始下一个休眠期；否则，关闭休眠定时器并进入活跃状态，依次服务等待在缓存队列中的任务。

1.2 系统模型

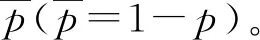
将t时刻备用模块中的任务总数称为t时刻的系统水平，表示为N(t)=i(i=0,1,…)。将t时刻主模块中的任务总数称为t时刻的系统阶段，表示为L(t)=j(j=0,1,…,c1+H)。将t时刻备用模块虚拟机所处的状态称为t时刻的系统相位，表示为J(t)=k(k=0,1)，其中k=0,1分别表示备用模块虚拟机处于休眠状态和活跃状态。{(N(t),L(t),J(t),t≥0)}构成一个三维连续时间马尔科夫链[11]，其状态空间Ω表示为

Ω={(i,j,k)|i=0,1,…,j=0,1,…,c1+H,k=0,1}。

令πi,j,k表示稳态下系统水平为i，系统阶段j及系统相位为k的概率分布。πi,j,k表示为

令πi(i≥0)表示稳态下系统水平为i的概率向量，则马尔科夫链{(N(t),L(t),J(t)),t>0}的稳态概率分布Π表示为

Π=(π0,π1,…)。

2 系统模型的稳态解析

马尔科夫链{(N(t),L(t),J(t)),t>0}的转移率矩阵表示为Q，系统水平从i(i=0,1,…)跳转到i′(i′=0,1,…)的转移率子阵表示为Qi,i′[12]。为了描述方便，引入符号Iu(u≥1)，表示u×u维单位阵。

1)Qi,i-1为系统水平由i减少到i-1的转移率子阵。

当i=1时，备用模块虚拟机既可能休眠也可能活跃。只有在备用模块虚拟机处于活跃状态的条件下，当其上的虚拟机服务完成一个任务后，系统水平才可能下降到0，此时，虚拟机进入休眠状态，一步转移率为μ2。

Q1,0为(2c1+2H+2)×(c1+H+1)阶矩阵，表示为

当i≥2时，备用模块虚拟机既可能休眠也可能活跃。只有在备用模块虚拟机处于活跃状态的条件下，当虚拟机服务完成一个任务后，系统水平才可能下降到i-1，此时，虚拟机仍保持在活跃状态。在2≤i≤c2和i≥c2+1的情况下，一步转移率分别为iμ2与c2μ2。

Qi,i-1为(2c1+2H+2)×(2c1+2H+2)阶方阵。

若2≤i≤c2，Qi,i-1表示为

若i≥c2+1，Qi,i-1表示为

2)Qi,i为系统水平保持不变的转移率子阵。

当i=0时，备用模块中的虚拟机一定处于休眠状态，只需分析主模块的变化规律。当主模块中到达一个任务时，一步转移率为nλ(1-p)。当1≤j≤c1时，若主模块服务完成一个任务，一步转移率为jμ1；若主模块中既无任务到达也无任务离去，一步转移率为-nλ(1-p)-jμ1。当c1+1≤j≤c1+H时，若主模块服务完成一个任务，一步转移率为c1μ1；若主模块中既无任务到达也无任务离去，一步转移率为-nλ(1-p)-c1μ1。

Q0,0为(c1+H+1)×(c1+H+1)阶方阵，表示为

当i≥1时，备用模块中的虚拟机处于休眠状态或者活跃状态。当1≤j≤c1时，若主模块服务完成一个任务，一步转移率为jμ1；当c1+1≤j≤c1+H时，若主模块服务完成一个任务，一步转移率为c1μ1。为了描述方便，引入二阶方阵αj,j-1。

若1≤j≤c1，αj,j-1表示为

αj,j-1=I2⊗jμ1，

若c1+1≤j≤c1+H，αj,j-1表示为

αj,j-1=I2⊗c1μ1。

当备用模块虚拟机处于休眠状态时，若休眠定时器到期，一步转移率为θ；若主模块中无任务到达，无任务离去，休眠定时器未到期，在0≤j≤c1和c1+1≤j≤c1+H的情况下，一步转移率分别为-nλ(1-p)-jμ1-θ与-nλ(1-p)-c1μ1-θ。当备用模块虚拟机处于活跃状态且主模块中无任务到达，无任务离去，备用模块中无任务离去时，若1≤i≤c2，在0≤j≤c1和c1+1≤j≤c1+H的情况下，一步转移率分别为-nλ(1-p)-jμ1-iμ2与-nλ(1-p)-c1μ1-iμ2；若i≥c2+1，在0≤j≤c1和c1+1≤j≤c1+H的情况下，一步转移率分别为-nλ(1-p)-jμ1-c2μ2与-nλ(1-p)-c1μ1-c2μ2。为了描述方便，引入二阶方阵βj,j。

若1≤i≤c2, 0≤j≤c1，βj,j表示为

若i≥c2+1, 0≤j≤c1，βj,j表示为

若1≤i≤c2,c1+1≤j≤c1+H，βj,j表示为

若i≥c2+1,c1+1≤j≤c1+H，βj,j表示为

当主模块中到达一个任务时，一步转移率为nλ(1-p)。

Qi,i为(2×c1+2×H+2)×(2×c1+2×H+2)阶方阵，表示为

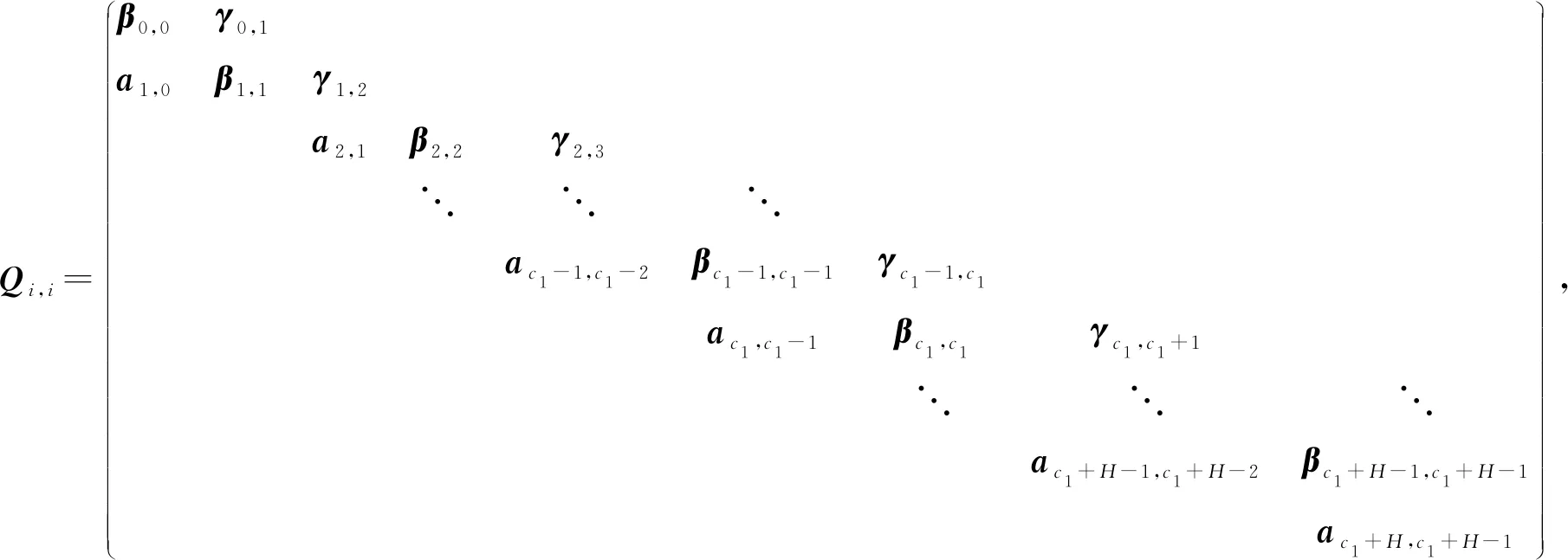
其中，γj,j+1=I2⊗nλ(1-p)。

3)Qi,i+1为系统水平由i增加到i+1的转移率子阵。

当i=0时，备用模块中的虚拟机一定处于休眠状态。当主模块中的可用容量为零时，新到达的任务进入备用模块，备用模块虚拟机仍处于休眠状态，一步转移率为nλ(1-p)。

Q0,1为(c1+H+1)×(2c1+2H+2)阶矩阵，表示为

当i≥1时，备用模块中的虚拟机处于休眠状态或者活跃状态。当主模块中的可用容量为零时，新到达的任务进入备用模块，此时，备用模块虚拟机保持在原状态，一步转移率为nλ(1-p)。

Qi,i+1为(2c1+2H+2)×(2c1+2H+2)阶方阵，表示为

由以上分析可知，转移率子阵Qi,i-1及Qi,i从系统水平c2开始重复，Qi,i+1从系统水平1开始重复。令Bi=Qi,i-1(1≤i≤c2-1)，B=Qi,i-1(i≥c2)，Ai=Qi,i(0≤i≤c2-1)，A=Qi,i(i≥c2)，C0=Q0,1及C=Qi,i+1(i≥1)。可将三维连续时间马尔科夫链{(N(t),L(t),J(t)),t≥0}的转移率阵Q表示为

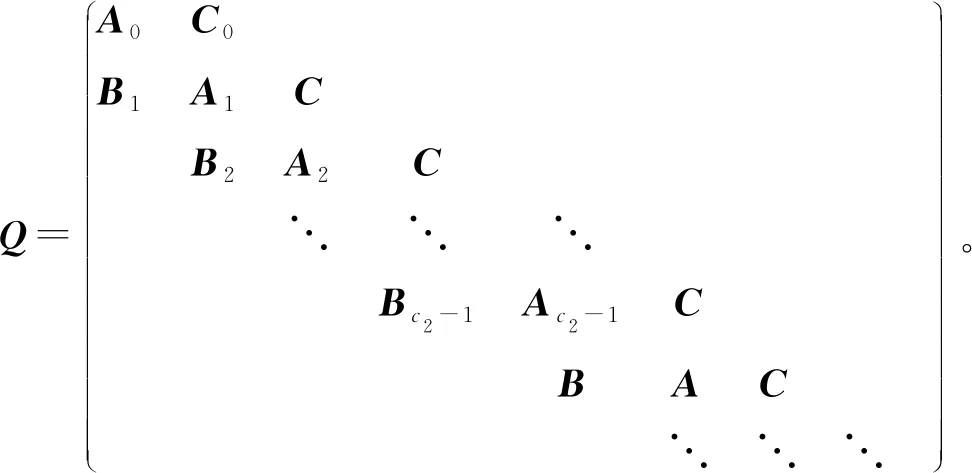
转移率阵Q中的状态转移只发生在相邻系统水平之间，因此，三维连续时间马尔科夫链{(N(t),L(t),J(t)),t≥0}是一种拟生灭过程[13]。该过程正常返的条件之一是矩阵方程R2B+RA+C=0的最小非负解R的谱半径小于1。

构造矩阵B[R]如下

由系统稳态方程及归一化约束条件[14]得出方程组如下

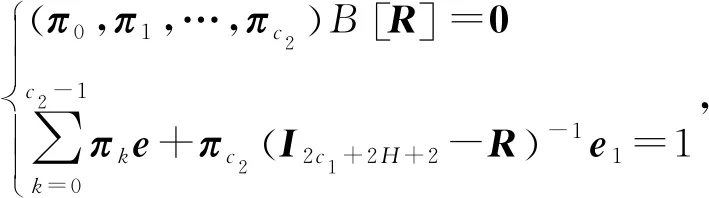
(1)

其中，e为(c1+H+1)+2(c2-1)(c1+H+1)阶全1列向量，e1为2c1+2H+2阶全1列向量。

运用高斯—赛德尔迭代法，求解方程组(1)，可得π0,π1,…,πc2的数值解，利用矩阵几何解形式πk=πc2Rk-c2,k≥c2+1进一步得到πk(k≥c2+1)的数值解。

3 性能指标与系统实验

3.1 性能指标

任务平均延时及系统节能率是评估MEC任务卸载策略的两个重要指标。

任务平均延时定义为任务从进入系统直到离开系统平均消耗的时间，即平均等待时间与服务时间的和。

任务在本地处理器接受服务的平均延时E[T0]为

(2)

卸载到MEC服务器上的任务首选进入缓存容量有限的主模块。若主模块中的任务数超过主模块中的虚拟机数，新到达的任务尝试进入缓存容量有限的队列中等待。在主模块中接受服务的任务平均延时E[T1]为

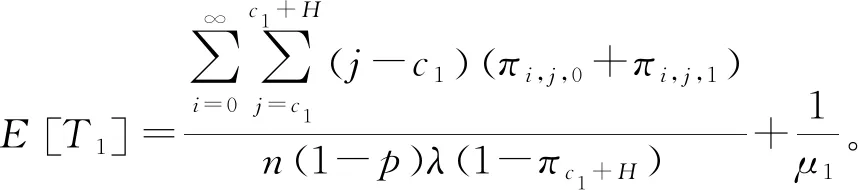
(3)

若主模块中的可用容量为零时，新到达的任务将进入缓存容量无限的备用模块中。在备用模块中接受服务的任务平均延时E[T2]为

(4)

每个移动设备产生的任务以概率p在本地处理器接受服务，以概率1-p在MEC服务器上接受服务。结合式(2)～(4)给出任务平均延时E[T]为

E[T]=pE[T0]+(1-p)((1-πc1+H)E[T1]+πc1+HE[T2])。

(5)

系统节能率S定义为单位时间内备用模块虚拟机处在休眠状态所节省的能量。令ω为空闲状态下备用模块的运行功率，ω0为休眠状态下备用模块的运行功率。备用模块在休眠状态的运行功率低于空闲状态下的运行功率，即ω>ω0。在所提出的MEC任务卸载策略中，能量节省产生于备用模块虚拟机的休眠状态。系统节能率S为

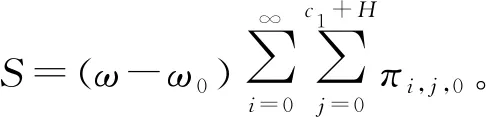
(6)

3.2 系统实验

为了验证MEC任务卸载策略的有效性，进行数值实验与仿真实验，在不同的任务到达率下，刻画本地分配概率对系统性能的影响。

基于MATLAB 2016a进行数值实验，揭示任务平均延时与系统节能率的变化趋势，验证MEC任务卸载策略的有效性。在Eclipse 2019环境下进行仿真实验，使用Java语言模拟200 000个任务的到达与离去过程，验证系统建模的合理性与模型解析的准确性。

基于数学理论分析的数值实验获得的是样本空间为无穷大时的极限结果。该结果的准确性与所采用高斯—赛德尔迭代法求解方程组的精度有关。基于机理模型的仿真实验获得的是样本空间有限条件下的统计结果。该结果的准确性与样本空间的大小有关。

参考文献[12]，同时考虑系统稳定条件，设置实验所用系统参数如表1所示。

表1 系统参数Tab.1 System parameters

图2刻画了卸载策略下任务平均延时E[T]的变化趋势。

图2 任务平均延时随任务到达率λ及本地分配概率p的变化趋势Fig.2 Average delay of tasks versus arrival rate of tasks and local allocation probability

固定任务到达率λ观察图2，在本地分配概率p从0.05变化到0.95的过程中，任务平均延时E[T]先呈现出下降趋势，在任务平均延时E[T]到达最低点之后，又呈现出上升趋势。当本地分配概率较小时，大多数的任务卸载到MEC服务器，随着本地分配概率逐渐变大，去往本地的任务数量逐渐变多，缓解了MEC服务器的负载压力，任务平均延时减小。当本地分配概率较大时，大多数的任务去往本地，随着本地分配概率逐渐变大，一方面，本地负载压力变大，使得任务平均延时增大；另一方面，MEC服务器因频繁休眠，服务能力减弱，也使得任务平均延时增大。

固定本地分配概率p观察图2，任务平均延时E[T]的变化趋势与本地分配概率p相关。当本地分配概率较小时，大多数的任务卸载到MEC服务器，随着任务到达率的逐渐变大，卸载到MEC服务器上的任务数量逐渐变多，降低了MEC服务器的休眠机会，增强了MEC服务器的服务能力，任务平均延时反而减小了。当本地分配概率较大时，随着任务到达率的逐渐变大，本地和MEC服务器的负载压力变大，使得任务平均延时增大。

图3刻画了卸载策略下系统节能率S的变化趋势。

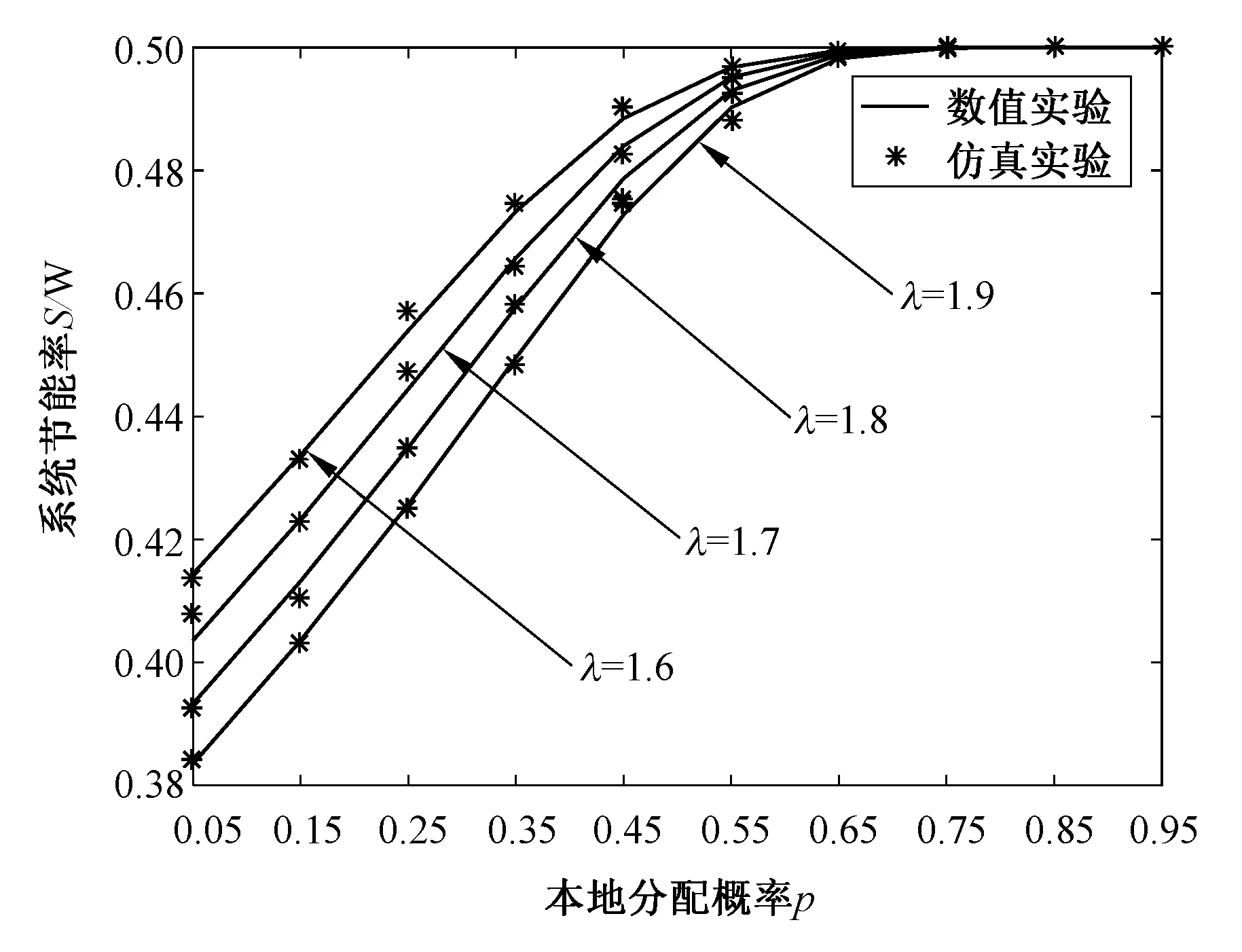
图3 系统节能率随任务到达率λ及本地分配概率p的变化趋势Fig.3 Energy saving rate of system versus arrival rate of tasks and local allocationprobability

固定任务到达率λ观察图3，在本地分配概率p从0.05变化到0.95的过程中，系统节能率S呈现先上升后不变的趋势。当本地分配概率逐渐变大时，卸载到MEC服务器上的任务数量变少，提高了MEC服务器的休眠机会，因此，系统节能率增大。当本地分配概率增大到一定程度时，只有少数任务卸载到MEC服务器，备用模块虚拟机几乎一直休眠，系统节能率达到极限。

固定本地分配概率p观察图3，系统节能率S的变化趋势与本地分配概率p相关。当本地分配概率较小时，大多数的任务卸载到MEC服务器，随着任务到达率的增大，MEC服务器的休眠机会降低，因此，系统节能率减小。当本地分配概率较大时，只有极少数的任务卸载到MEC服务器，即使任务到达率增大，也很难将备用模块虚拟机由休眠状态唤醒至活跃状态，因此，系统节能率不变。

由上述分析可知，任务到达率及本地分配概率对任务平均延时和系统节能率有很大影响。对于给定的任务到达率，合理设置本地分配概率，能够实现响应性能与节能水平的合理均衡。

4 策略参数优化

只研究任务平均延时或者系统节能率，难以给出最优的MEC任务卸载策略[15]。令任务平均延时的影响因子为η1，系统节能率的影响因子为η2，构造成本函数F(p)如下

F(p)=η1(E[T])2-η2S。

传统的鸽群算法[16]容易陷入局部最优。为了改善这一问题，提出一种融合“教与学”过程的改进的鸽群算法。基于“教与学”过程能够引导鸽群的飞行方向，改善候选解的质量，避免陷入局部最优。使用改进的鸽群算法，以成本最小为目标，优化本地分配概率。改进的算法步骤如下：

Step 1:初始化鸽群位置(本地分配概率)的左边界pmin与右边界pmax，鸽群数量X，地图和指南针算子的最大迭代次数Y1，地标算子的最大迭代次数Y2，指南针因子φ。设地图和指南针算子的当前迭代次数t1=1，地标算子的当前迭代次数t2=1。

Step 2:在鸽群位置的约束范围[pmin,pmax]内，初始化鸽群速度vi(i=1,2,…,X)，计算鸽群位置pi(i=1,2,…,X)。

vi=rand；%rand表示取0到1之间的随机数

pi=pmin+vi×(pmax-pmin)；

Step 3:计算系统成本函数F(pi)(i=1,2,…,X)，给出鸽群个体适应度值。

F(pi)=η1(E[T])2-η2S；%E[T]与S分别为分配到本地的概率为pi时的任务平均延时和系统节能率

Step 4:找出使系统成本最小的本地分配概率p*。

Step 5:执行地图和指南针算子，计算鸽群速度vi(i=1,2,…,X)与鸽群位置pi(i=1,2,…,X)，基于“教与学”过程更新鸽群位置pi(i=1,2,…,X)。

vi=vi×exp(-φ×t1)+rand×(p*-pi)；%计算鸽群速度vi

pi=pi+vi；%更新鸽群位置pi

τ=round(1+rand)；% round为四舍五入运算符

随机选取两个鸽子位置pa与pb；%a,b= 1, 2, …,X

pi=pi+rand×abs(pa-pb)；%abs为绝对值运算符

Step 6:检查地图和指南针算子的迭代条件。

ift1

t1=t1+1，goto Step 5；

endif

Step 7:执行地标算子，更新鸽群位置pi，找出最优的鸽子位置p*。

按系统成本值由小到大排列鸽群位置pi(i=1,2,…,X)；

X=ceil(X/2)；%ceil为向上取整运算符

sum1=0；

sum2=0；

fori=1 :X

sum1=sum1+pi×F(pi)；

sum2=sum2+F(pi)；

endfor

center=ceil(sum1/(X×sum2))；

fori=1 :X

pi=pi+rand×(center-pi)；%更新鸽群位置pi

if(pi>pmax)‖(pi

pi=pmin+rand×(pmax-pmin)；

endif

ifF(pi)

p*=pi；%更新最优的鸽子位置p*

endif

endfor

Step 8:检查地标算子的迭代条件。

if(t21)

t2=t2+1，goto Step 7；

endif

Step 9:输出最优的本地分配概率p*及最小系统成本F(p*)。

以参数η1=5，η2=0.100，X=80，pmin=0.001，pmax=0.999，Y1=50，Y2=40及φ=0.700为例，利用改进的鸽群算法找出最优的本地分配概率p*以及最小系统成本F(p*)，结果如表2所示。

表2 本地分配概率的优化结果Tab.2 Optimization results of local allocation probability

相比于MEC服务器，本地移动设备自身处理能力有限，能够接纳的任务不能太多。当系统的任务到达率增加时，为了保证网络用户的服务质量，将有更多的任务卸载到MEC服务器，因此，最优本地分配概率下降。另一方面，随着系统的任务到达率的增加，任务平均延时增大，系统节能率变小，这些都是使系统成本变大的原因。由此可知，表2的数值结果所揭示的最优本地分配概率及最小系统成本的变化规律是合理的。

5 结论

综合考虑网络用户的响应性能及系统节能水平，融合虚拟机分簇与同步周期性休眠机制，面向 MEC 提出了一种任务卸载策略。基于备用模块虚拟机周期性休眠机制，建立带有同步多重休假机制的连续时间排队模型，给出了任务平均延时及系统节能率等性能指标的解析式。数值与仿真的实验结果表明，合理的本地分配概率可以同时保证用户的响应性能和系统的节能水平。构造系统成本函数，引入“教与学”方法，改进鸽群优化算法，给出了本地分配概率的优化方案，实现了系统成本的最小化。