广义Riccati矩阵方程异类约束解的两种迭代算法

陈世军

(阳光学院，福建 福州 350015)

0 引言

在时变广义系统的稳定性和具有对称循环结构的广义大系统的最优控制中存在求解Riccati矩阵方程(RME)解的问题，尤其是求解广义Riccati矩阵方程的约束解问题[1-2].RME的一般形式可表示为

(1)

近年来，许多学者对非线性矩阵方程的数值解进行了研究，并给出了一些有效的算法.例如：Long等[3]证明了求解非对称Riccati方程迭代算法的收敛性；张凯院等[4]用牛顿算法和修正共轭梯度算法研究了Riccati矩阵方程的对称解问题；Y.Q.Lin等[5]分析了非线性代数Riccati方程迭代算法的收敛性；Y.F.Ke等[6]利用交替方向法求解了矩阵方程的非负解；周富照等[7]等给出了子矩阵约束下矩阵方程的正交投影迭代解.本文借鉴非精确牛顿算法(In-Newton算法)、修正共轭梯度算法(MCG算法)和正交投影迭代算法(OPA算法)原理，建立了一种求广义方程(1)的对称和反对称约束解的迭代算法，并通过数值算例比较了两类算法的计算效率.

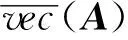
1 建立求方程(1)Ω1-2解的非精确Newton算法

为了计算方便，引入如下记号：

根据ψ(X)、φX(Y)和γ(Y)的表达式和矩阵乘法的性质，易推导出

ψ(X+Y)=ψ(X1+Y1,X2+Y2)=ψ(X)+φX(Y)+γ(Y)，

(2)

其中φX(Y)是ψ(X)在点X沿Y方向的Frechet导数.

由Newton算法的基本原理可知，当Y1和Y2的范数较小时，可以舍去式(2)右端关于Y1和Y2的高次项γ(Y)，即用式(2)右端的线性部分近似可得ψ(X+Y)≈ψ(X)+φX(Y).设(X1,X2)∈Ω1-2是方程(1)的近似解，则求方程(1)的一组解(X1,X2)等价于求校正值(Y1,Y2)∈Ω1-2使ψ(X+Y)=O，并可以把求方程(1)的解X近似为求方程(3)的解(Y1,Y2).方程(3)的表达式为:

φX(Y)=-ψ(X).

(3)

本文利用Newton算法求方程(1)Ω1-2解的步骤如下：

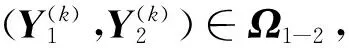
Step 3 计算X(k +1)=X(k)+Y(k)，令k∶=k+1，转Step 2.

参照Newton算法，本文给出求方程(1)Ω1-2解的非精确Newton算法如下：

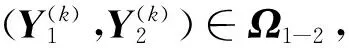
(4)

Step 3 计算X(k +1)=X(k)+Y(k)，令k∶=k+1，转step 2.

2 建立求方程(3)Ω1-2解和最小二乘解的MCG算法

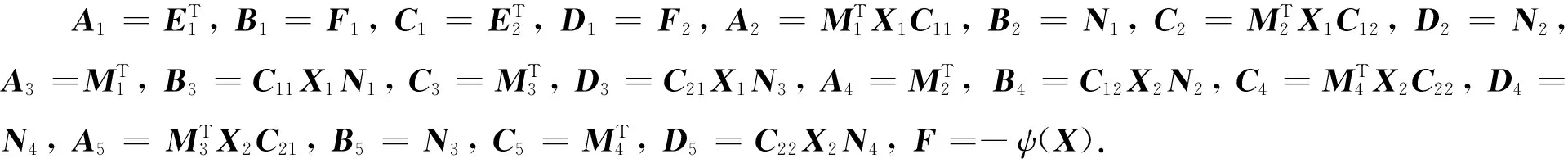
(5)

其中Ai,Bi,Ci,Di,F∈Rn ×n(i=1,2,3,4,5).本文主要解决下面两个问题：

问题Ⅰ设方程(5)有Ω1-2解，求(Y1,Y2)∈Ω1-2，使(Y1,Y2)满足方程(5).

2.1 求解问题Ⅰ的MCG算法

为建立求解问题Ⅰ的MCG算法，首先引入如下记号：

求解问题Ⅰ的MCG算法1的步骤如下:

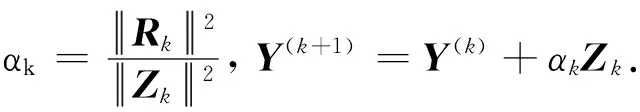
Step 4 令k∶=k+1，转Step 2.

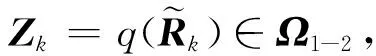
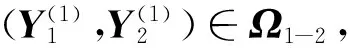
2.2 求解问题Ⅱ的MCG算法

当MCG算法1中断时，需要求解问题Ⅱ.首先构造与方程(5)等价的约束正规矩阵方程，并且把求方程(5)的Ω1-2最小二乘解转化为求其约束正规矩阵方程的Ω1-2解；然后参照MCG算法1，建立求方程(5)Ω1-2最小二乘解的MCG算法，即求问题Ⅱ的解.引入如下记号：

定理2[9]求解问题Ⅱ等价于求矩阵方程f(Y)=N的Ω1-2解，且该矩阵方程一定有Ω1-2解.

参照MCG算法1的原理，建立求方程f(Y)=N的Ω1-2解，即建立求解问题Ⅱ的MCG算法2.MCG算法2的计算步骤如下：

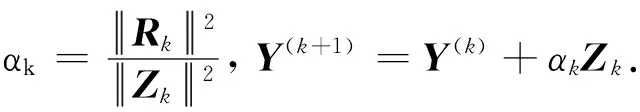
Step 4 令k∶=k+1，转Step 2.

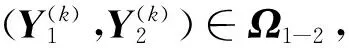
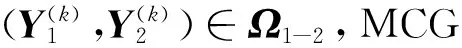
3 建立求方程(3)Ω1-2解和最小二乘解的OPA算法

MCG算法虽然给出了有限步的收敛结果，但是没有给出收敛率的估计.OPA算法也是一种求解矩阵方程约束解的有效算法，其被广泛运用于信号处理、矩阵方程的约束解求解等问题中.参照OPA算法的基本原理，本文建立的求问题Ⅰ的OPA算法1的步骤如下：

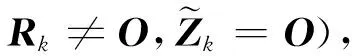
Step 4 令k∶=k+1，转Step 2.

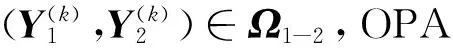
由定理4可知问题Ⅰ不相容，矩阵方程(5)无Ω1-2解.根据定理2并参照OPA算法1，本文建立的求问题Ⅱ的OPA算法2如下：

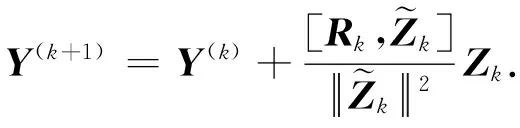
Step 4 令k∶=k+1，转Step 2.

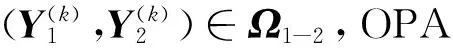
4 数值算例

分别用两个数值算例比较文中给出的In-Newton-MCG算法和In-Newton-OPA算法.参照文献[4]的计算方案，本文将In-Newton算法作为外迭代算法，将MCG算法和OPA算法作为内迭代算法.In-Newton-MCG算法2和In-Newton-OPA算法2的初始矩阵Y(1)取算法1终止时的Y(k).本文设计的求方程(1)Ω1-2解的计算方法如下：

In-Newton-MCG算法：

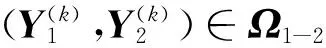
(6)

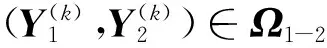
Step 3 计算X(k +1)=X(k)+Y(k)，令k∶=k+1，转Step 2.

In-Newton-OPA算法：

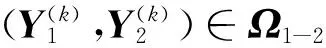
Step 3 计算X(k +1)=X(k)+Y(k)，令k∶=k+1，转Step 2.

例1用本文建立的In-Newton-MCG算法和In-Newton-OPA算法求方程(1)的一组Ω1-2解和最小二乘解，其中系数矩阵为：

Ei=Fi=Ci j=I(i,j=1,2)，Mi=Ni=I(i=1,2,3,4)，

数值实验利用Matlab软件进行.实验时取η=0.1，系数矩阵阶数取n=4，外迭代Newton算法的终止准则为10-7，MCG算法和OPA算法的终止准则为10-8.MCG算法和OPA算法的最大迭代次数为n0=4 999，非精确Newton算法的初始矩阵为X1=4In和X2=On，MCG算法和OPA算法的初始矩阵均为Y1=Y2=On.用t、k0、k1、k2和error分别表示计算时间、非精确Newton算法的迭代次数、MCG算法1和OPA算法1的迭代次数、MCG算法2和OPA算法2的迭代次数和误差范数.两种算法的计算结果如表1所示.

表1 两种算法求方程(1)Ω1-2解的结果

当MCG算法和OPA算法的初始矩阵取Y1=Y2=On时，In-Newton-MC G算法和In-Newton-OPA算法均可得到方程(1)的一组解：

上述两种算法虽然都能求得方程(1)的解，但从表1可以看出，在相同的条件下In-Newton-MCG算法的效率高于In-Newton-OPA算法的效率.

例2修改例1中的部分系数矩阵，即使Mi=Ni=O(i=2,3,4)，其余系数矩阵同例1.求方程(1)的一组Ω1-2解.计算取η=0.9，非精确Newton算法的初始矩阵为X1=X2=On，MCG算法和OPA算法的初始矩阵为Y1=Y2=On，且在计算实验过程中依次增加系数矩阵的阶数.两种算法求方程(1)Ω1-2解的结果见表2.

表2 两种算法求方程(1)Ω1-2解的结果

由表2可知，当选择不同的非精确Newton算法的初始矩阵时，In-Newton-OPA算法失效，而In-Newton-MCG算法始终有效.因此，在今后的研究中我们将探讨In-Newton-OPA算法在什么条件下失效，以及在什么条件下In-Newton-OPA算法比In-Newton-MCG算法有效.