信息熵在日益复杂的世界中的重要应用
高剑波,刘飞燕,张建方
(1.北京师范大学地理数据与应用分析中心,北京 100875;2.杭州城市大数据运营有限公司,杭州 310000;3.中国科学院大学经济与管理学院,北京 100190)
1 引言
我们生活在一个信息时代吗?若把增加知识和减少不确定性的任何东西都视为信息,那么答案显然是肯定的,以下事件也无疑支持了这个答案:
(1)存储设备从144KB 的软盘,100MB 和250MB的Zip驱动器,发展到几十个GB的优盘;
(2)Google,Amazon,以及Facebook 等新兴社交网络公司的巨大成功;
(3)互联网上越来越多的免费音频、文本和图像;
(4)互联网上呈指数增长的基因组学、蛋白质组学、地球物理学、天体物理学、和其它科学的数据正在给科学和技术的众多领域带来革命性变化;
(5)Google Books 项目把过去人类出版书籍的4%数字化了[1‑3],GDELT(Global Database of Events,Language,and Tone)项目则把全世界所有英语和非英语的新闻媒体的数据收入其中[4]。
信息熵的概念对以上所有事件的发生都起了重要作用。特别是,通过遥感技术(尤其是人造卫星)获得的地球物理数据对天气预报的日益准确起了主要作用。
信息熵是重要且普遍存在的,这也使好奇之士不禁要问,信息熵与Boltzmann(波尔兹曼)和Gibbs (吉布斯)的热力学熵之间有什么关系。由于热力学熵的概念最初是被发明出来用于描述气体粒子的运动,所以讨论信息熵和热力学熵之间的关系似乎限定在非生命和唯物论的科学范畴才比较好(如文献[5])。然而,这个策略不太可行,科学和技术都在向更小和更大的尺度发展,而且世界内部的关联越来越紧密。为了更好地解决新兴的科学、技术和环境问题,需要讨论信息熵的起源,找出信息熵和热力学熵的关键区别,理解信息熵在复杂性理论(包括混沌理论和分形理论)中的作用,推测信息熵可能会起重要作用的新领域。这些都将是本文的主要话题。为方便非专业人士理解本文,我们将聚焦于对概念的讨论。然而,为使本文对经验丰富的研究者同样有用,我们也不回避一些数学上的讨论。
2 信息熵的起源
信息熵最早是由克劳德·香农(Claude Shannon)提出来作为通信(即各种信息传输)的一个理论模型[6]。在通信中有两个技术问题:1)源信息如何被量化和表达?2)系统容量是多少,即在给定时间内系统能传输或处理多少信息?
在通信中,第一个关键发现是需将讯息视为随机的,即在接收前对接收者是未知。实际上,如果听众总是能确切地知道讲话者接下来会说什么,那么他们之间的交流就毫无意义。因此,自然就引出下面的通信方案:1)收集通过某信道发送来的所有讯息{Yi,j,j=1,2,…,Ns,i=1,2,…,M},并将它们记作一个随机事件集(A1,A2,…,An);2)记第i条讯息可能出现的概率为pi≥0,满足=1。
在概率论中,(A1,A2,…,An)被称作是一个事件的完备系统[7]。若扔一颗骰子,则它们对应于(1,2,3,4,5,6);若抛一枚硬币,则它们对应于(正面,反面)。若骰子和硬币是均匀的,则得到等概率的分布分别为(pi=16,i=1,2,…,6)和(pi=12,i=1,2);若骰子或硬币不是均匀的,那么概率将取不同值。在通信中,抛硬币相当于一个二元问题(比如是或否,黑或白,红或蓝,等等)。当一条讯息被接收,则从通信方案A=中得到的平均信息量可由信息熵给出,其定义为:

为了方便,若pj=0,则pjlogpj=0.公式(1)有很多性质,尤其是取对数时,它为信息量的定量化提供了一个方便的单位。当对数的底为2时,这个单位就叫做比特(bit):对于一个等概率的二元问题,是或否、对或错的概率均为0.5,不论什么情形,信息量都刚好为一个比特。比特是任何计算机中数据存储和处理的基本单位。
如果仅有一个pj为1 而其它pj均为0,那么H=1.此时,我们面对的是一个确定性体系,在读取由通信设备发送的讯息时得不到任何知识。另一个极端是所有事件发生的概率均为1/n,这时信息熵H达到最大值logn.由四个核苷酸A(腺嘌呤)、T(胸腺嘧啶)、C(胞嘧啶)、G(鸟嘌呤)组成的一个DNA 序列接近于均匀分布,于是,每个碱基平均约包含2 比特信息[8]。
通过使用冗余的思想,数十年的努力获得了很多优秀的纠错码来有效地表达通过信道传输的讯息。因此,第一个问题“源信息如何被量化和表达”已经完全解决了。(MIT 的著名数学家Peter Shor 通过一个巧妙的方法把冗余的思想推广到量子计算,并开发了一个量子纠错设计[9]。)
第二个问题“信道的容量是多少”,其答案也已经由Shannon 在其经典文章中给出。通过使用信息熵概念的一个自然引申—互信息(mutual information),信道容量可由下面的公式精确地给出:
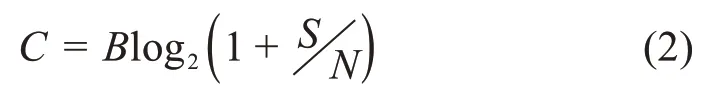
其中,B是以赫兹为单位的信道带宽,是信噪比。互信息本质上是对如何比较信道上接收到的讯息与发送的讯息进行衡量。
虽然这里不去证明公式(2),我们还是解释一下其原理以加深对通信的理解。已知信号和噪声的功率分别为S和N,那么总功率为P=S+N。在模拟信号情况下,我们把一个信号波划分成若干段,每段代表一条讯息。这里必须为信道考虑最坏的情形,即所有讯息是等可能的,因此信道在连续地传输新讯息。最大可能的段数由下面的公式给出:
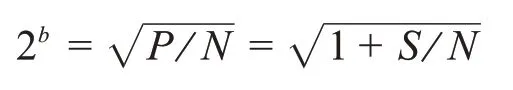
在这里,每条讯息由b个比特来表达。如果我们在时间T内对b比特水平做M次测量,那么收集到的信息的总比特数为:
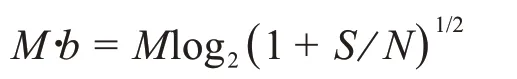
信息传输率(I每单位时间比特)为:
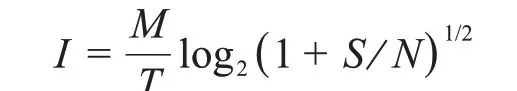
注意到的最大可能值就是最高的实际采样率2B.自然就得到公式(2)。
值得注意的是,当B→∞,容量C不会变为无限大,因为噪声的功率也与B成比例。记N=μB,其中μ为每单位带宽的噪声功率,由于
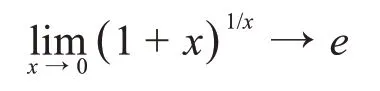
所以得到:
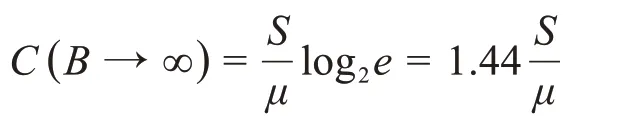
3 经典热力学中的熵
毫无疑问,“熵”这个词最早出现在经典热力学中。经典热力学探讨整个系统的状态变量,比如气体的压力、体积和温度,其经常出现的一个数学方程是

其中,dQ为温度,T时热转移的量,dH是熵的变化。热力学第二定律断言,在一个封闭系统中,dH不可能减小。经典热力学对相关材料精细的微观结构不做任何假定。
相反地,经典统计力学则设法对材料的精细结构进行建模,并从这些模型来预测经典热力学的规律。举个例子,气压可以解释成气体分子朝墙壁作匀速冲撞,这些分子如同小而硬的理想弹性球体。即使少量气体,其包含的粒子数N仍巨大。事实上,N可由作为原始量级的阿伏伽德罗常数(the Avogadro constant,NA=6.022 × 1023)得到。想象一个相空间,其坐标由每个粒子的位置和速度确定,于是,这些气体粒子的相空间就是6N维空间的一个子区域。假定对于一个确定的能量,相空间中每个小区域都有相同的概率,则Boltzmann(波尔兹曼)发现下面的量就是熵:

其中,P是给定能量的相空间中任何等可能小区域的概率,kB是Boltzmann常数。
在设法处理能量不确定的系统时,吉布斯(Gibbs)提出了“巨正则系统”,其本质是具有不同能量的Boltzmann 相空间的全体。吉布斯(Gibbs)推导出熵的公式为:
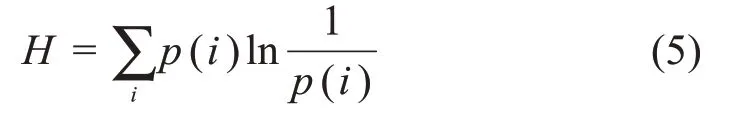
其中,p(i)是各相空间的概率。在表达上,公式(5)与公式(1)相同。因此,一些研究者会把信息熵看作是一个多余的术语也就不奇怪了。
然而,数学形式相同并不意味着含义相同,就像理查德·哈明(Richard Hamming)在其很有意思的一本书《The Art of Probability》中所强调的[10],信息熵和热力学的熵最根本的不同是:信息熵是通过一组具有任意概率的事件集合来计算的,而在热力学中,一般假定气体粒子等概率地占据容器的任何区域。因此,信息熵是比热力学熵更广义的一个概念。为帮助进一步理解,记住这点非常有帮助:迈伦·崔巴士(My‐ron Tribus)从信息熵中推导出了热力学的所有基本定律[11]。更重要的是,热力学熵可能不太适合描述基因组学和蛋白质组学的序列以及很多涌现的复杂行为,而信息熵是复杂理论的一个基本组成部分[12,13,14],自然能够量化生物学序列中的信息量[8,13]。
4 最大化熵的概率分布
熵的一个最重要应用是,通过最大化熵来确定与科学和工程中众多现象相联系的初始分布。均匀分布就是这样一种分布,然而它不是唯一的。依赖于约束,其它分布也可以最大化熵。为便于讨论,我们首先需要把基于离散概率的信息熵推广到基于概率密度函数的信息熵,后者由下面定义的微分熵(differen‐tial entropy)给出:
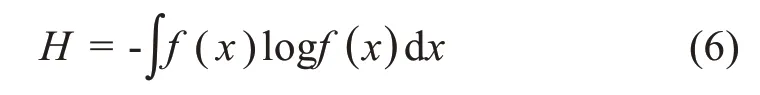
为简单起见,这里仅列出两种在相应约束下可以最大化熵的初等分布。
(1)指数分布,其概率密度函数为:
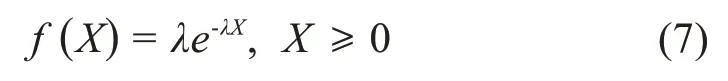
在随机变量X的期望为1/λ的约束下,最大化熵的分布是指数分布。
指数分布能最大化熵的这个特性也许是为什么在数学和物理中经常遇到指数分布的主要原因之一。例如,用来定义泊松过程的时间或空间间隔服从指数分布,而马尔可夫过程的逗留次数也服从指数分布[12]。指数分布与遍历的混沌系统也很相关,因为混沌系统的重现次数服从指数分布[15,16]。指数律在物理学中扮演了一个更为基本的角色,因为统计力学和量子力学中的基本定律都可表达为指数分布,而有限自旋玻璃系统就等价于马尔可夫链。
(2)均值μ和方差σ2给定时,最大化熵的分布是正态分布N(μ,σ2)。
正态分布能最大化熵的根本原因是中心极限定理——正态分布可以被认为是一个吸引子,因为充分多的具有有限期望和方差的独立随机变量的样本均值将渐近地服从正态分布。
5 熵与复杂性
广义来说,任何既不完全规则也不完全随机的行为都可以被称为涌现复杂行为(emerging complex be‐havior)。代表性的复杂行为包括混沌运动和分形行为,后者包括具有长程相关的随机过程,这个过程是迷人的1现象的一个子类[17,18]。
为了方便下面的讨论,我们首先把不同形式的运动按其复杂性从低到高排列:定点运动,周期运动,准周期运动,混沌运动,湍流,随机运动。有趣的是,在固体材料中能观察到一个类似的序列:晶体,准晶体,分形,和非周期随机形式。尤其是丹.舍特曼(Dan Shechtman)因为发现了准晶体而获得了2011年的诺贝尔化学奖。在动力学界,准周期运动是早已熟知的,根据这两个序列的相似性,可能有人早已经预测过准晶体的存在。从丰富程度上来看,分形形状要比准晶体丰富得多。
5.1 分形
欧几里德几何是关于线、平面、三角形、正方形、圆锥体、球体,等等。这些不同对象的一个共同特点就是规则性,没有一个是不规则的。然而,云是球体吗?山是圆锥体吗?岛屿是圆吗?答案显然是否定的。为寻找这些问题的答案,曼德勃罗(Mandelbrot)开创了一个新的科学分支——分形几何[19]。
目前,分形的一个直觉性定义是令人满意的:一个不规则但在很多或者所有尺度上具有自相似特性的集合。自相似性意味着对象的一个部分和其它部分或全体都是相似的。也就是说,如果我们用显微镜观察一个不规则对象,不管我们把物体放大10 倍,100 倍,甚至1000 倍,我们总能发现类似的对象。为了更好地理解,想象我们正在观察空中漂浮的一片白云,我们的眼睛保持不动,总是一直盯着同一个方向。一段时间过后,我们盯着的那片云有一部分已经飘走了,看到的是那片云的不同部分,然而我们感觉或多或少还是原来的那片云。
在数学上,自相似或分形可以用幂律关系来刻画,幂律关系在log‑log尺度中可以变换成一个线性关系。要理解幂律关系是如何构成自相似感知的基础,设想在空中有大量气球飞来飞去,不同尺寸气球的数量服从一个重尾的幂律分布:

见图1,作为人类,我们本能地聚焦于那些大小适合于眼睛的球——太小的看不到,而太大的又妨碍我们的视野。现在假定最适合我们的尺寸是r0.当然,我们的眼睛不可能敏锐到能区分r0与r0+dr的不同,其中 |dr|≪r0.然而我们有能力分辨如2r0,r0和r0/2等尺寸的飞球。气球的哪个方面会决定我们的感知呢?这本质上取决于尺寸为2r0,r0和r0/2 的气球之间的相关丰度:

图1 大小服从帕累托分布P[ X ≥x ]=( 1.8x)1.8的盘片的随机分形
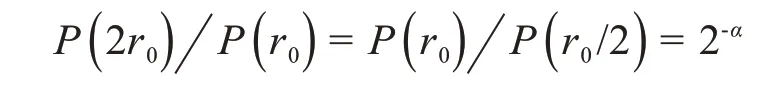
注意到上面的比率独立于r0.现在假设我们通过显微镜来看球,把所有的球都放大100 倍。现在我们的眼睛聚焦于尺寸为2r0/100,r0/100和r0/200的气球,我们的感知仍将由这些尺寸的气球的相对丰度所决定。由于是幂律分布,相对丰度仍是相同的——我们的感知也是这样。
5.2 Tsallis非广延熵和幂律行为
解释幂律和分形行为普遍性的一个引人注目的方法就是最大化Tsallis熵。Tsallis熵是根据巴西杰出的物理学家Tsallis的名字命名的[20,21]。为解释其思想,我们先把Shannon的信息熵推广到由下式定义的Renyi熵:
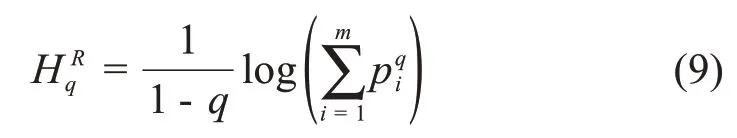
在Renyi 熵中引入参数q是为了调整概率的大小。比如,当q≫0 或q≪0 时,大或小的概率值决定了公式(9)的右边。Tsallis熵由下面的公式定义:
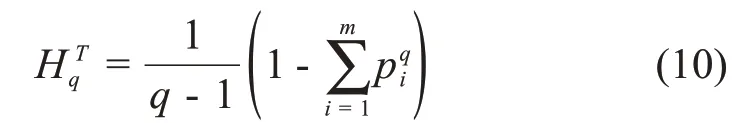
通过一些简单关系,Tsallis 熵可以与Renyi 熵和Shannon熵联系起来:
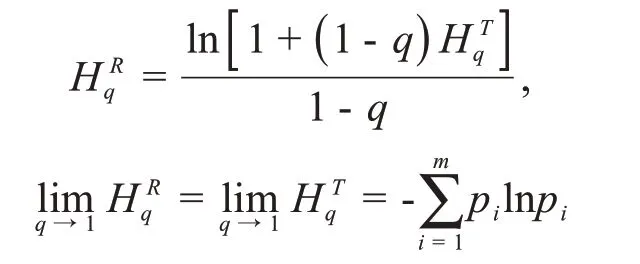
然而,Tsallis 熵的关注点不同——它是为了找出一个明确的q值(一般不等于1)来很好地描述既不规则又不完全混沌或随机的现象。对于包含两个独立子系统的复合系统,Tsallis熵是非广延的,该复合系统的Tsallis熵不等于两个子系统的Tsallis熵之和。迄今为止,已经组织过很多研讨会和学术会议来讨论Tsl‐lis非广延统计学。
对于连续概率密度函数,通过最大化Tsallis 熵,可以得到Tsallis分布[22]:

其中,Zq是标准化参数,β与二阶矩相关。当53 图2.用Tsallis分布拟合海杂波雷达回波数据的代表性结果.这里,(q,β)分别为(1.34,43.14)和(1.51,147.06)(参见[21]) 分形行为不局限于几何对象,它们还可以表示时间上波动(比如股市价格波动)和混沌运动。混沌的含义与直觉理解一致,这里,我们将把混沌限定在严格的数学含义中,即指数分岔: 其中,d(0)表示在0时刻任意两个轨迹之间的一个很小的距离,d(t)是它们在t时刻的平均距离,λ1>0是最大的正李雅普诺夫(Lyapunov)指数。这个性质也被称作对初始条件的敏感依赖性,这也是迷人的蝴蝶效应的起源:由于波士顿的一只蝴蝶拍动了翅膀,纽约的晴天可能在不久后的某时被雨天取代。这个性质在图3 中生动地表现出来:在混沌洛仑兹吸引子中初始很接近的点迅速分开并很快分布在吸引子的周围。 图3 混沌洛仑兹系统中的整体预测:粉红色的是2500个初始点,在2,4,6个时间单位后变成红色,绿色,蓝色 为了更好地理解对初始条件的敏感依赖性,我们考虑在圆上的映射: 其中,xn是正数,mod 1 表示把2xn的小数部分保留下来作为xn+1.这个映射也可以看成是一个贝努利变换或二进制变换。假如把初始条件x0用二进制表示: 其中,各个数字aj为1或0。于是 等等。因此,一开始远离小数点右边的一个数字,比如第40位数(对应于2-40≈10-12),它对初始值x0的大小影响非常小,然而它最终将升为第一个,也是最重要的数字。 一个混沌运动通常可描述为一个奇怪吸引子。所谓“奇怪”是指指数分岔;所谓“吸引子”是指运动的有限性。在相空间中,这种无休止的延展和折回经常导致潜在吸引子的分形结构。这个吸引子的分形或容量的维数可由以下决定:把含有这个吸引子的相空间分成具有线性尺寸ε的众多单元,记其中非空的单元数为n(ε),则 这里,D0称作盒维数(box‑counting dimension)。 这个盒维数的概念可以被一般化,即得到一个称之为广义维谱(generalized dimension spectrum)的维数序列。通过把概率pi分配给第i个非空单元就得到了这个维数序列。计算pi的一个简单方法就是用niN,其中ni是第i个非空单元中点的数量,N是吸引子的总点数。设非空单元数为n,则: 其中q为实数。一般地,Dq是q的非增函数。当q=0 时,=n,D0其实就是盒维数或容量维度。D1给出了信息维度(Information Dimension)DI: 以上考察可以推广到监测一个混沌吸引子的详细时间演化。我们所需要做的就是把相空间分为大小为ε的小盒子,计算非空盒子i被轨迹经过的概率pi,从而计算出Shannon熵。对于很多系统,当ε→0,信息随时间线性增加[23]: 其中I0是初始的熵,为了简单起见可取为0,这里的K是柯尔莫哥洛夫‐西奈(Kolmogorov‑Sinai(KS))熵。 为了加深理解,我们考虑动力系统的三种情形:(i)确定性且非混沌的系统;(ii)确定性的混沌系统;(iii)随机系统。对于情形(i),在系统演化过程中,相轨迹一直是很接近的;在时间T后,邻近相点仍非常接近,并且能一起被分进相空间的其他小区域。因此,在信息上没有改变。对于情形(ii),由于指数分岔,在时间T后,系统可用的相空间区域数N∝e(∑λ+)T,其中λ+是正的Lyapunov指数。假定所有这些区域均是等可能性的,于是,pi(T)~1,信息方程变为: 因此,K=.更一般地,如果这些相空间区域未被等概率地经过,则: 然而,Grassberger 和Procaccia[24]认为等概率一般是成立的。最后,对于情形(iii),容易预见,在短时间后,整个相空间都会被经过。因此,I~lnN;当N→∞,有K=∞。 以上讨论说明:尽管热力学熵对描述分形和混沌行为也许不是很有用,但Shannon 的信息熵始终是一个基本组成部分。容易理解,KS 熵的精确定义仍将基于Shannon的信息熵,只需把公式(18)中的pi(T)替换为在随后d个时刻轨迹分别落在盒子i1,i2,…,id内的联合概率。 很久以来,有限的柯尔莫哥洛夫(Kolmogorov)熵经常被认为是确定性混沌的标志,在很多应用中一直被遵循。这方面的混沌研究可以用一个比方来总结:很多研究者正在野沙滩上追逐混沌这只野兽,一个人叫喊“这里有一个足印”;另一个回应“这里有另一个”……,一段时间后,一些仔细的人发现那些只是他们自己的足印。在计数器例子中,1f随机过程最有说服力,它们有分形的维度和有限的Kolmogorov 熵,因此被误认为是确定性混沌[25,26]。 如果思考更深入一些,就容易知道,通过有限的随机数据是不可能得到一个无穷大的KS 熵。这就是为什么从噪声中识别混沌一直被认为是一个经典且困难的问题[27‑29]。要根本解决这个问题,除了求助于多尺度方法,别无他法。解决该问题最显而易见的方法之一是依赖尺度的Lyapunov 指数(SDLE).SDLE 是尺度参数的函数,因此完全不同于普通的Lyapunov 指数,后者是一个数。在多尺度的复杂性测量中,SDLE 拥有最丰富的尺度规则(scaling laws)。例如,对于混沌运动,SDLE 是一个常数,表明了确实的指数分岔。然而,对于1过程,SDLE是一个幂律。因此,从噪声中识别混沌不再是个问题。而且,通过一个整体预测方法,SDLE 可以把动力系统中很多不同种类的熵联系起来。更多的细节可以参考[30‑32]。 最后我们指出,由于能对随机性程度进行量化,因此信息熵是一个确定性的复杂性测度。有时在描述一类既不规则又不完全随机的行为上,它被认为是不理想的。作为一个替代选择,统计复杂性已经提出来,对于既不高又不低的随机性[33,34],它能被最大化。有趣的是,在这个积极演进的领域,信息熵仍是一个重要组成部分[35,36]。 尽管混沌动力系统有分形的性质,但分形行为还有一个重要的子集——随机分形行为,它完全不同于确定性混沌动力系统。认识到随机分形行为的基础是随机,并且很多非混沌但随机的行为也许可以用随机分形来建模,高剑波等主张:(1)综合地运用混沌和随机分形的理论来解决一系列真实世界碰到的问题;(2)用多尺度方法在一个广泛的尺度范围内同时描述复杂信号的行为[12]。 多尺度方法有很多,其中就包括随机分形理论,其关键原理是尺度不变性,即信号的统计行为独立于时间或空间的间隔长度。使用尺度不变性,在分形尺度规则(scaling laws)起作用的广泛尺度上,只要一个或几个参数就足以描述信号的复杂性。因为参数个数少,所以分形分析是最节约的多尺度方法之一[12]。其它多尺度方法包括:在前面已做过简要讨论的SDLE;有限大小的Lyapunov 指数[37‑39];(ε,τ)熵[40];多尺度熵[41]。对单一的时间序列数据进行分析和建模,这些方法可认为是足够的。比较缺乏的是研究两个或更多系统(包括两个或多个时间序列数据)之间详细的交互作用的工具。 虽然物理学基本定律中时间都是可逆的(即如果把所有方程中的时间t都替换成-t,关系依然成立),但时间不可逆的过程是普遍存在的。从冷热水的混合,到火柴燃烧和玻璃打碎,普通现实世界的经验告诉我们,不考虑基本物理定律的数学公式,时间之矢只指向一个方向。 为了解决这个悖论,Boltzman发展了Boltzman熵的概念和H定理。正如我们讨论的,Boltzman 熵是所有可能的微观状态数(或相空间容量)的对数。H定理支配着(负)熵的时间演化,意味着熵必须是常量或随时间增加。这两个概念一并考虑得出了关于时间方向性的一个约束。 Boltzman 的设计尽管非常成功,但也出现了争议[42,43]。历史上,Ernst Zermelo提出了坚决的反对,基于Poincaré 的重现定理,他指出一个封闭的动力系统最终必然要返回到任意接近初始状态。因此,最终每个系统将是可逆的,熵不可能总是增加。 在直觉上,一个封闭系统回复到初始状态的Poincaré 重现时间肯定长得难以想象。Richard Feyn‐man(理查德·费曼)证明,“在一百万年内,这将是不可能发生”[44]。Vladimir Arnold 认为这将比太阳系的年龄更长[45]。据说Boltzmann 自己也说:“你要长久等待!”[46]。近来,这个时间长度的一个定量估计已经由高剑波给出[15],如下: 其中,τ是抽样时间,r是相空间中要被再次经过的子域的大小,DI是已经讨论过的信息维度。对于完全随机的气体运动,正如我们讨论的,DI可取与6NA的相同量级,其中NA是阿伏伽德罗常数。因此,如果取r~1/10,那么重现时间的量级约为1036×1023τ。这个时间实在长得与现实毫不相关了! 尽管对Boltzmann方案的反对与现实并不完全相关,但相反的研究却更有成效—C′edric Villani,一位天才的法国数学家,同时也是2010年菲尔兹奖得主,能从Boltzmann 方程中计算熵的产生,并找到了平衡的收敛速率[47]。 非常不幸的是,Boltzmann 自杀了。不过,一个与Boltzmann 同时代的冷静智者Willard Gibbs 没有把自己拴在热力学第二定律令人沮丧的含义中。Gibbs沉着地得出了重现时间肯定非常长的结论,但可能有机会观察到将违反热力学第二定律的过程。实际上,这样的过程在短时间内,在小纳米尺度系统中能轻易地被观察到[48]。其可能性事实上与公式(20)有很大关系——指数是DI-1 而不是DI.当DI很大时,DI与DI-1 本质上没有差别;但当系统很小时,DI-1 取代DI将使重现时间更短。 在一个封闭的自然系统中,违反热力学第二定律的情况也许不容易观察到。负熵流与其说是在生命之外,倒不如说是在支配生命——正如Erwin Schrödinge 所断言“生命需要负熵”[49]。Lila Gatlin 认为在生命系统中,只要信息被存储,熵就会减少[13]。更准确地,我们也许会说,当基因密码被精确执行,外部刺激被神经元适当处理,生命就产生作用。正如杰出的数学家和理论物理学家Roger Penrose 在他的畅销科学读物《The Emperor′s New Mind》中所讨论的,这种负熵的根源是太阳[50]。 正如预期的,信息熵已经在科学和工程的几乎每一个领域都找到了有意思的应用。在最后一节,我们将解释熵如何应用于复杂数据的分析,并推测信息熵会在哪些前沿领域起关键作用。 当一个复杂系统的概率分布已知时,通过使用公式(1)可以很容易计算出信息熵。如果只有一条时间序列数据,那么如何计算熵?答案是通过Lempel‑Ziv(LZ)复杂度[51,52]。 LZ 复杂度及其导数方便快速计算,并且与Kol‐mogorov 复杂度密切相关[53,54],在刻画复杂数据的随机性方面已有许多应用。 为了计算LZ 复杂度,首先需要把数值序列变换成符号序列。最常用的方法就是通过把信号与某个阈值Sd比较[55],进而把信号转变为0‑1 序列。也就是说,当信号值大于Sd,就把信号映射为1,否则就映射为0.一个较好的选择是把信号的中位数作为Sd[54]。当使用多个阈值时,可以把数值序列映射为一个多符号的序列。值得说明的是,如果原始的数值序列是一个非平稳的随机游走类过程,那么应该分析其平稳的差分序列而非原始的非平稳序列。 得到符号序列后,然后可以对该序列进行解析以获得不同的词,并对这些词编码。令L(n)为这些词的编码的序列长度,LZ复杂度可以这样来定义: 这与Kolmogorov复杂度的内涵一致[53,54]。 有很多方法可以用来对符号序列做解析。一个常用的方案是由LZ 复杂度的原作者提出[51,52]。为方便起见,我们称之为方案一。另一个常用的方案是Cover和Thomas提出的[57],我们称之为方案二。为方便起见,我们在二项式序列背景下描述它们。 方案一:令S=s1s2…sn代表一个有限长的0‑1 符号序列;S(i,j)表示S的一个从位置i开始在位置j结束的子序列,其中i≤j,S(i,j)=sisi+1…sj,且当i>j时,S(i,j)={},即空集。令V(S)代表序列S的词典,即所有子序列S(i,j)的集合(即所有的S(i,j),i=1,2,…,n;j≥i)。比如,令S=001,那么V(S)={0,1,00,01,001},这里,解析的过程是从左到右扫描序列。子序列S(i,j)与由截止到位置j-1 的S的所有子序列组成的词典V(S( 1,j-1))比较。如果S(i,j)已经出现在了V(S( 1,j-1))中,那么就把S(i,j)和V(S( 1,j-1))分别更新为S(i,j+1)和V(S(1,j)),过程重复一次。如果子序列S(i,j)没有出现在词典中,那么在S(j)后打一个点,以显示新元素的结尾,把S(i,j)和V(S( 1,j-1))分别更新为S(j+1,j+1)和V(S(1,j)),过程继续。这个解析操作从S(1,1)开始,直到j=n结束,n是符号序列的总长度。比如,有一个序列是1011010100010,可以解析为1∙0∙11∙010∙100∙010∙.按照惯例,有一个点置于符号序列最后一个元素的后面。在这个例子中,不同的词的个数是6. 方案二:序列S=s1s2…sn被逐步扫描,并被改写为一个词的级联w1w2…。wk这样被选出来的:w1=s1,wk+1是之前未出现的最短的词。换句话说,wk+1是某个词wj的扩展,wk+1=wjs,这里0 ≤j≤k,s 要么是0要么是1.上面序列的例子,1011010100010被解析为1∙0∙11∙01∙010∙00∙10.因此,总共有7个不同的词。这个数字比方案一中的数字要大1. 通过方案二得到的词很容易编码。一个简单方法是[57]:令c(n)表示在解析原序列时的词的数量。对每个词,我们分别用log2c(n)个比特去描述这个词的前缀的位置和1个比特去描述最后一个位置。针对上面的例子,令000 来描述一空的前缀,那么序列可以被描述为:( 000,1)( 000,0)( 001,1)( 010,1)( 100,0)( 010,0)(001,0)编码序列的总长度为L(n)=c(n)[ log2c(n)+1 ].因此公式(21)变为: 当n非常大时,c(n) ≤nlog2n.[51,57]把公 式(22)中的c(n)用nlog2n替换,可以得到: 除了c(n)可由方案一得到,CLZ的常规定义就是依据公式(23)中的函数。特别地,由方案一得到的c(n)比由方案二得到的值小。然而,编码由方案一得到的词要比方案二使用更多的比特。我们推测由公式(21)定义的复杂度对两种方案是相似的。其实,从数值上,我们发现CLZ对n的函数依赖性(基于公式(22)和(23))对两种方案是相似的。 对于无限长度的序列,LZ 复杂度等于Shannon熵。特别地,对于无限长的周期序列,LZ 复杂度为0。然而,当一个周期序列的长度是有限的,LZ 复杂度比0要大。在大部分的应用中,信号是有限长的。因此,要找到一个合适的方法来保证一个有限长的周期序列的LZ 复杂度为0,并且一个完全随机序列的LZ 复杂度为1.这个问题最早由Rapp 等人研究[58]。近来,Hu 等人使用分析学的方法再度来考虑这个问题[59]。特别地,他们为随机等概率序列以及任意周期m的周期性序列推导出了LZ 复杂度的公式,并提出了一个做标准化的简单公式。图4 显示了把LZ 复杂度用于癫痫发作检测的脑电图(EEG)数据分析。我们观察到,LZ 复杂度尽管简单,但与混沌理论中的相关熵和相关维一样有效,可用于检测癫痫发作。有关更多详细信息,请参见[59]。此外,为了更深入地了解脑电图分析中不同复杂性测度之间的联系,请参见[60]。 图4 一位病人的EEG信号中LZ复杂度(a1,a2),标准化LZ复杂度(b1,b2),相关熵(c1,c2),相关维(d1,d2)随时间的变化。(a1⁃d1)是通过把EEG信号分成500个点的小窗口得到的;(a2⁃d2)是使用2000个点的窗口。(a1,a2)中的垂直虚线是由医学专家确定的癫痫发作时间。 信息熵在哪里必不可少呢?我们相信肯定是那些与人类行为有联系的领域。在那些情形中,作为第一步,使用信息熵主要不是提供一个公式来对不确定性进行量化;而是将帮助研究者全面理解一个重要问题,即为了应用信息熵而去定义一个完整的事件系统。对于数据驱动的复杂数据的多尺度分析[12],综合性是指导原则,也是产生长期持续影响的先决条件。 在推测之前我们注意到,随着科学的发展,目前不确定或未知的事物将来可能会部分或完全地知晓,于是信息熵的作用将会减小。这情形与普渡大学谢越宁教授(Yuch‑Ning Shien)在与作者高剑波私人交谈中所深思的相似:“当暗物质的某种明确形式在未来被发现时,那么暗物质的数量就会减少。”为了更好地理解这一点,我们把从DNA 序列中估计信息熵作为一个具体的例子:基于核苷酸基的分布[8],熵接近2比特;而若把序列相关关系考虑进来的话,熵会显著小于2比特[61]。 一个更复杂的情形是在心理学中使用信息熵。在上世纪五六十年代,信息理论在心理学中一度很流行,之后就影响不再,因为对神经元处理信息有了日益深刻的理解[62]。但近来,在心理学中对信息论的兴趣开始复苏,目的是更好地理解与不确定性相关的焦虑[63]。这个新模型聚焦于作为人类主观经历的潜在活动和知觉的加权分布,并把较低的熵分派给较强的目标。本质上来说,这个模型是分层的,神经科学在最底层工作,主观决策牵涉多个层。用Erwin Schrödinger 的话说,一个层级模型在本质上就是“次序基于次序”[49]。 现在考虑信息熵在环境科学和工程上的潜在应用。具体来说,让我们从中国普遍的PM2.5 污染开始。首先,我们来考虑PM2.5 污染的物理学。已知PM2.5 硫酸盐在大气中会停留三到五天。根据平均风速,比如5米/秒,几天的停留时间产生了“长距离传送”和更均匀的空间图样。平均来说,PM2.5 颗粒从最初形成它们的气体中能被传送到直至1000 多公里以外。这也是导致香港冬天PM2.5 污染的主要原因[64]。因此,从物理上看,系统研究PM2.5 污染,包括在源头的形成速率、PM2.5 水平随风速的变化、大气传送,等等,将非常有意思,从而决定应该采取什么措施才能把PM2.5 污染控制在一定范围内。当然,这项研究工作将有很多不确定性。但信息熵甚至热力学熵都应该会起一定的重要作用。 接下来,我们考虑严重PM2.5 污染的后果。首先是对健康的负面影响,这已经在媒体中被广泛讨论过。西方研究者发表的关于PM2.5 污染影响的医学研究只是普通地考虑了较低浓度PM2.5 颗粒的影响。而在中国的很多城市,PM2.5 浓度经常连续很多天都超标。因此每一个人不禁会问一个问题:PM2.5 颗粒对健康的负面影响与PM2.5 颗粒的浓度是线性关系还是非线性关系?如果是非线性的,那么某种分岔可能发生,也就是说,当PM2.5 浓度超过一定水平,健康问题将急剧增加。接下来的问题是这种污染所导致的健康问题的医疗费用。更进一步,PM2.5 污染对户外动物,尤其是鸟的危害有多大?它们没有任何措施保护自己免受有害的且分散在很大空间范围的PM2.5颗粒的危害。 这种费用不只是简单地停留在医疗水平上。严重的污染导致雾霾天气更频繁。雾霾天气使可见度降低,迫使公路关闭,恶化了交通堵塞,引起更多的交通事故和伤亡,影响购物,使成千的航班取消,等等。显然,这种混乱可能与熵的急剧增加有关。为了说服政府责任机构采取果断行动来减少PM2.5 污染,综合地考虑PM2.5污染问题将是关键。 接下来,我们讨论一些经济发展与熵的产生之间的关系。尽管许多国家的GDP 取得了显着进步,但必须指出的是,到目前为止,在开发经济增长模型时很少关注熵的概念。这些模型包括包括马克思的经济理论[65]及赢得了诺贝尔经济学奖的Solow‑Swan 的新古典增长模型[66,67]。随着我们的生存环境正面临着日益加重的危险,现在正是认真解决可持续性增长这一关键问题的时候了。 为更好地把握上述问题,我们必须讨论熵在经济学中究竟意味着什么。一般的理解就是把熵与经济数据的一些分布联系起来[68]。的确,负收入分布的熵能非常好地预测经济下滑,包括近来巨大的金融危机[69]。一个新兴领域——经济物理学(Econophys‐ics),正尝试着为经济学开发一个类似于热力学的学科,其中,能量和熵分别与资本和生产函数相联系[70]。然而,这样的观点还太僵硬,因为同样数量的钱,用法不同,会导致完全不同的结果。例如在2012年,亿万富翁、高尔夫球球手泰格.伍兹的前妻决定把新买的1200万美元的别墅拆毁重建,因为她认为这幢别墅对她来说太小。还是在2012年,超级飓风桑迪刚刚过去,纽约市的一些穷人由于缺少食物正在为生存挣扎。一些富人则为其它不同目的而抗争——因为飓风桑迪把他们的地下室给淹没了,所以他们正忙于消费那1000 美元一瓶的葡萄酒。本文的观点是,要在经济学中巧妙地讨论熵,必须综合评价所有可能性以及它们带来的积极和消极结果。某一增长过程的浪费和破坏的结果应该和熵的大量增加相联系。 这是一个信息爆炸的时代。这里的关键是巧妙地利用数据——据麦肯锡估计[71],如果美国卫生保健部门能够创造性地有效利用大数据来提高工作效率和质量,则该部门每年能创造3000 亿美元以上的价值;在欧洲发达国家,仅仅通过使用大数据,政府管理者就能在运营效率改进上节省1490 多亿美元,这还不包括使用大数据减少诈骗、差错和增加税收的收入;如果利用好私人服务数据,就能获得大约6000 亿美元的消费盈余。为了人类的幸福,从大数据中最大化地利用有用信息将非常关键。 致谢 作者感谢中国科学院力学所郑哲敏院士的引导和启发。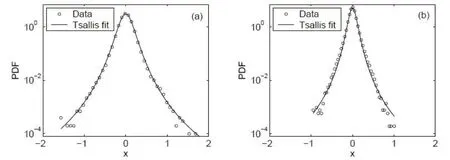
5.3 混沌


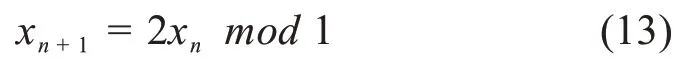
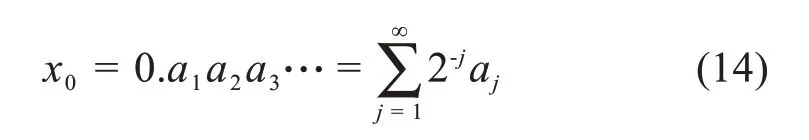
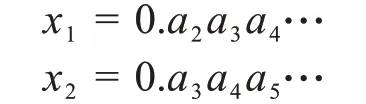
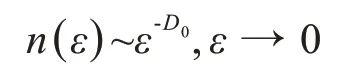
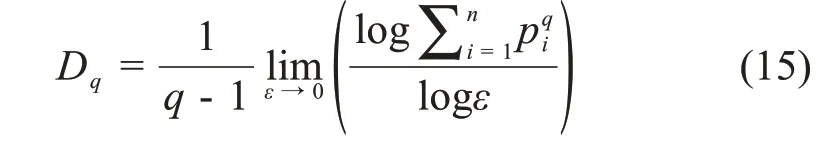

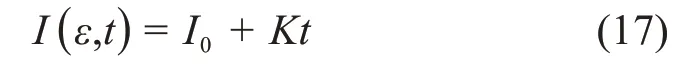
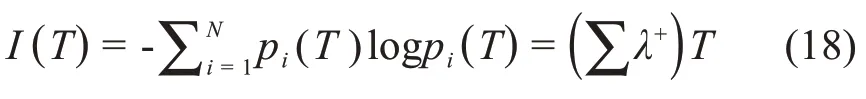

5.4 从噪声中识别混沌
5.5 统计复杂性
5.6 多尺度分析
6.时间之矢

7 内部关联世界的熵
7.1 估计复杂数据的信息熵:Lempel⁃Ziv复杂度

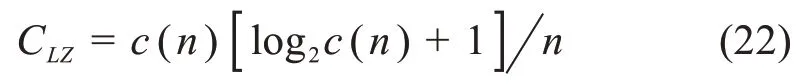
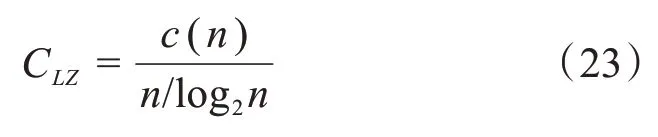

7.2 未来展望

