负压条件下柱形爆炸罐内爆炸波传播规律

汪泉，陆军伟，李志敏，林朝键，李雪交，程扬帆，李瑞

(1.安徽理工大学 化学工程学院，安徽 淮南 232001；2.安徽省爆破器材与技术工程实验室，安徽 淮南232001；3.安徽理工大学 土木建筑学院，安徽 淮南 232001)

0 引言

炸药在自由场中爆炸时，会在微秒量级时间内产生高温高压气体。爆炸产物会猛烈地向四周扩散并压缩周围空气，形成冲击波。与敞开的自由场环境不同，炸药在密闭环境下爆炸时，冲击波的传播状态比自由场要复杂得多，冲击波会出现多次反射叠加，相应的峰值压力也会相对于自由场明显增加。表征炸药爆炸的参数主要有峰值超压、比冲量、爆炸波传播速度、质点速度、正压作用时间等。一般认为，炸药爆炸的破坏方式以冲击波破坏为主。为了找出峰值超压、比冲量和爆炸波传播速度之间的关系，揭示冲击波传播规律与破坏机制，国内外学者进行了大量实验和理论研究，提出了一系列计算冲击波超压的半经验公式[1-4]。

当空气压力或温度等外界条件发生变化时，峰值压力、比冲量和爆炸波传播速度这些参数也会发生相应的变化，尤其当环境压力降低时，冲击波的传播特性与常压情况下将有所不同。有关不同压力环境下爆炸冲击波的传播规律，国内外学者各自开展了不同研究，并取得了一些很有价值的研究成果。在实验研究方面，黄亚峰等[5]、杨雄等[6]研究了真空环境下铝粉对含铝炸药爆炸场压力和温度的影响规律；张广华等[7]使用JO-8炸药研究了真空环境下的爆炸威力，并与常压情况下进行了对比分析；Silnikov等[8]基于爆炸波相似准则，研究了高能炸药的冲击波参数与空气压力的关系，分析了初始压力对爆炸载荷准静态分布的影响；朱冠南等[9]采用抽真空装置，测试了低压环境下膛口冲击波传播规律，实验结果表明：膛口的冲击波压力会随着环境压力的降低而近似线性减小。在真空爆炸数值模拟方面，李科斌等[10]采用ANSYS/AUTODYN有限元分析软件对不同真空度下炸药爆炸波近场特性进行了数值模拟研究；王树有等[11]根据不同海拔的大气环境给出了空气的状态方程参数，采用ANSYS/AUTODYN有限元分析软件建立了高原环境下的仿真模型，分析了不同海拔下的爆炸冲击波传播特性；宋水舟[12]利用ANSYS/LS-DYNA有限元分析软件分别模拟了球形药包、扁平状炸药在不同真空度下中心起爆时冲击波的传播规律；Veldman等[13]将实验和数值模拟方法相结合，研究了3种初始压力(81.4 kPa、101.3 kPa、156.5 kPa)环境对爆炸冲击波的峰值超压和正压作用时间的影响；姚成宝等[14]利用仿真软件模拟冲击波在不均匀介质中的传播，并分析了空气初始压强、密度等对冲击波传播的影响；谢雪腾[15]通过试验和数值模拟分别对海拔200 m和4 500 m的冲击波传播特性进行了研究，发现高原效应对冲击波的传播规律有明显影响。虽然国内外有关真空环境下爆炸的数值模拟研究有一些研究，但是有关受限空间内不同真空度下爆炸波传播规律的实验研究还未见报道，此方面缺乏系统性的实验研究，负压(真空)环境下的爆炸理论体系尚未构建。

基于此，本文研制了小型可调真空度的爆炸罐，开展了单发8号工业电雷管内爆炸情况下的爆炸波传播规律研究，分析了不同真空度条件下爆炸压力载荷特征和比冲量传播规律，并与常压情况下进行对比分析。所得实验与分析结果可为真空条件下内爆毁伤、爆炸焊接等工程应用提供理论参考。

1 爆炸罐内爆炸波传播过程分析

炸药在罐体内爆炸后，爆炸产物迅速压缩周围气体，导致压力在极短时间内迅速上升，压力达到最大值。随着冲击波继续向前传播，当冲击波碰到容器壁面或者容器底部和角隅等处会出现叠加、汇聚等情况而发生反射，根据容器结构不同，出现反射情况也不同。当爆炸波发生反射时压力会急剧增大，最高可能达到初始爆炸波压力的数倍以上，根据反射类型不同，爆炸波反射强度也不同[16]。当容器内压力降低时，其传播状态也会发生改变，但随着爆炸波传播，其能量在罐体内会逐渐衰减。图1给出了爆炸波在罐体内不同压力环境下的传播示意图，图1(a)为真空环境下的传播示意图，图1(b)为常压下的示意图。

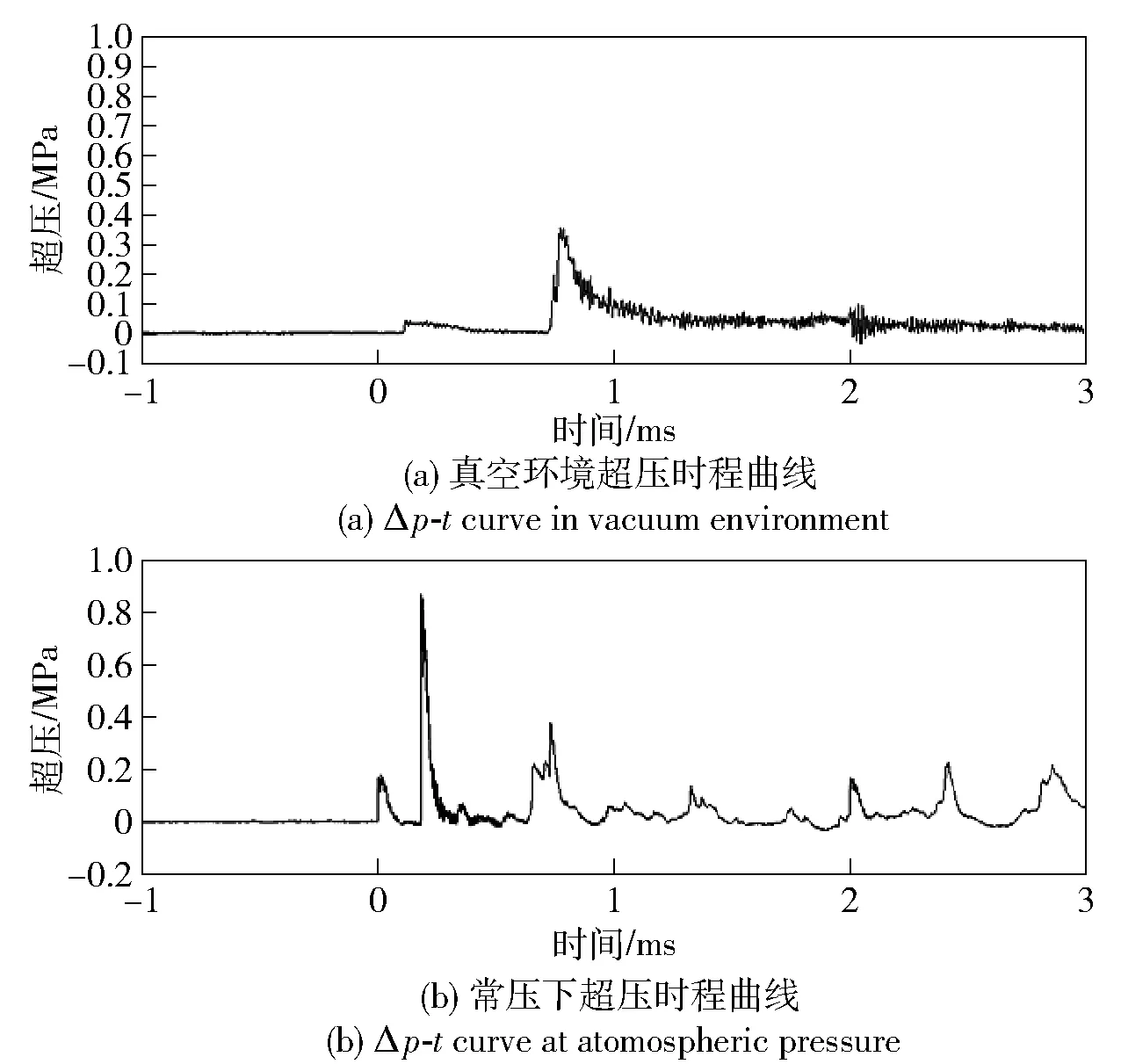
图1 不同初始压力下罐体内爆炸波传播超压-时间曲线示意图

2 小型抽真空爆炸罐内爆炸波传播特性实验研究

2.1 实验系统

实验所用装置为小型圆柱形、可调真空度爆炸罐，罐体高43 cm，内部直径32 cm，壁厚0.6 cm，容积34.8 L，对称面两侧有圆柱形观察窗，向外伸出约为10 cm.爆炸源为单发8号工业电雷管，聚能穴朝下，雷管底部距离罐体底端4.1 cm，与传感器接触面距离29.03 cm，垂直于罐体底部。测试装置由压电式压力传感器、信号调理仪、示波器组成。压力传感器布置在罐体轴向，其高度可在轴向根据需要进行调整，位于雷管正上方。实验装置如图2所示。

图2 实验装置

2.2 实验结果与分析

2.2.1 峰值超压变化规律

在固定雷管高度情况下，分别测量不同真空度下的爆炸波超压。爆炸波超压Δp的计算可通过以下公式得到[16]：

(1)

式中：Vm为示波器的峰值电压(V)；Sq为压力传感器的灵敏度(V/MPa)，经过两次校准后取平均值为716.55 mV/MPa.

把第1个爆炸波传播到传感器接触面的时间设为0 ms时刻，通过改变爆炸容器内真空度，测得罐体内不同初始压力下的Δp-t曲线如图3所示。

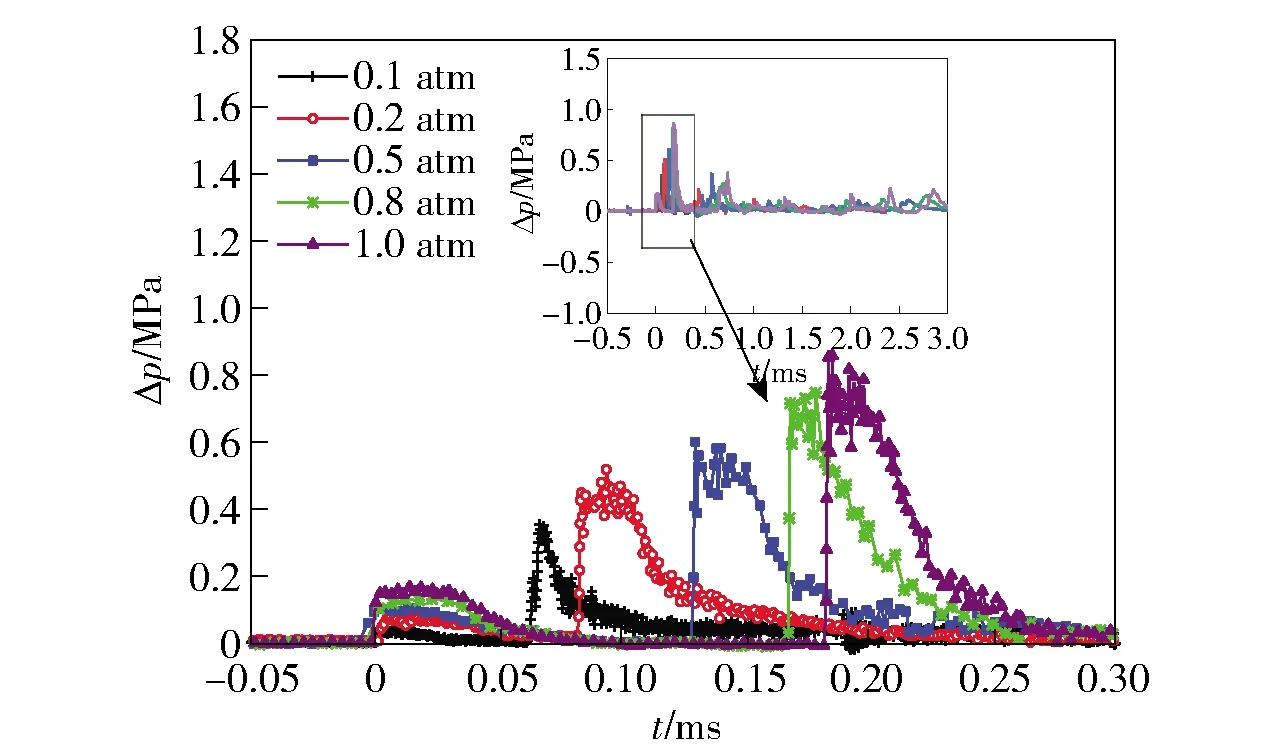
图3 不同初始压力下爆炸波的Δp-t曲线

根据以上爆炸波超压峰值，得到爆炸波的第1超压峰值和第2超压峰值随罐体内初始压力变化如图4所示。

图4 爆炸波的第1超压峰值和第2超压峰值随罐体内初始压力变化

由图3和图4分析可知，与自由场爆炸冲击波传播规律不同，罐体内爆炸波由于受到容器壁面的约束，会出现爆炸波反射叠加的情况，出现多个爆炸波压力峰值。第1个压力波峰值的出现是雷管爆炸产生的压力波直接作用于压力传感器所致，第2个压力波峰值是雷管爆炸后产生的压力波先传播到罐体底部，然后产生反射。此时，爆炸波压力峰值有明显的上升。

由图3和图4还可以看出：随着罐体内初始压力的降低，第2个压力波峰值的到达时间会提前；爆炸罐内部真空度会对爆炸波传播状态产生显著的影响。在不同的真空度条件下，当比例距离不变时，爆炸波压力峰值会随着容器内部压力的降低而降低，其波形的变化曲线趋于一致。可见，减小罐体内部气体介质的密度可有效降低爆炸波的毁伤作用。当罐体内压力降至0.1 atm时，罐体内的空气较常压相比已经非常稀薄，爆炸产生的能量传播很大程度上依赖于爆炸产物，且由于缺少空气介质，此时爆炸波能量传播衰减迅速，较难形成多次反射。

2.2.2 爆炸波峰值超压变化理论分析

(3)暂堵压井胶塞在川中高温含硫井的带压换阀门作业中进行了现场应用，泵注胶塞体系后4 h，油压由59 MPa降至29 MPa，解堵后液体顺利返排，黏度≤5 mPa·s，暂堵压井获得成功。

为了定性分析不同初始压力对爆炸波超压的影响，可以利用爆炸波参数之间的关系式对容器内部初始压力与冲击波压力的关系进行定性分析。当炸药爆炸产生的爆轰波向外部膨胀时，与空气等介质相接触，便形成了初始冲击波。在这个过程中，爆炸产物参数都在不断变化且时间极短，难以给出精确的表达式，但是可以对某些参数进行合理的假定，从而得到冲击波初始参数的计算方法。

爆轰产物的膨胀是由C-J点开始的，由于炸药爆炸形成的C-J压力pC-J到与介质接触形成初始冲击波这一过程时间极短，可以近似看作理想气体的等熵膨胀过程。

对于产物向空气中飞散的情况，可以假设作用过程是一维的，对初始分界面各参数进行考虑，用以下两条绝热线代替实际过程中的膨胀绝热曲线[17]：

pvn=pHvH,pK≤p≤pH，

(2)

(3)

式中：v为爆炸产物的速度；n为多方指数，n=3；pH、vH为爆轰波阵面处的爆轰产物参数；pK、vK为K点处的爆轰产物参数，其值可以通过爆轰波Hugoniot方程来确定；k为等熵指数，可取值为1.2.

爆炸产物速度可由(4)式进行计算[17]，

(4)

式中：vx为初始冲击波产物的膨胀速度，x为爆轰产物与空气介质的分界面；D为炸药爆速；cK为K点处的质点速度；px为初始冲击波压力，可通过(5)式进行确定[17]，

(5)

结合(4)式和(5)式，可以得到有关vx的方程式如下：

(6)

综合(4)式～(6)式进行分析可知，当空气的密度减小即空气压强减小时，爆炸产物的膨胀速度会增大。再观察(5)式可知，在炸药性质不变情况下，空气的初始密度越大，初始冲击波强度越大。初始冲击波速度Dx可由(7)式进行简化计算：

(7)

由(7)式可以看出，vx越大，相应的Dx就越大，即空气初始密度越小，其冲击波初始速度就越大。当然，分析过程均认为n和k的值是不变的，此种情况下的分析具有一定的理想性。但是对于定性分析仍然可以得到正确的结论。此结论与相关文献[10，12]数值模拟结论一致。

2.2.3 爆炸波速度变化规律

为了便于分析罐体内初始压力对爆炸波传播速度的影响，从爆炸波传播到压力传感器的整个过程认为爆炸波速度是不变的。通过对爆炸波的传播时间及距离进行记录，可以得到其传播平均速度。表1所示为不同环境压力下波峰时间差及爆炸波速度。

表1 不同环境压力下波峰时间差及爆炸波传播平均速度

由表1可以看到，随着罐体内初始压力的降低，爆炸波到达同一测点的时间逐渐减小，其平均传播速度增大。

2.2.4 比冲量变化规律

爆炸波产生的比冲量i可根据(8)式进行计算[16]：

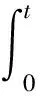
(8)

式中：t为压缩相持续时间。

图5给出了在1 atm初始压力下，第1爆炸波比冲量i1和第2爆炸波比冲量i2的变化规律。由图5可以看出，比冲量i1和i2均随着容器初始压力的降低而降低，且比冲量i1和i2均有相同变化趋势：在0.5 atm之前，比冲量值i1和i2随初始压力下降得比较缓慢，在0.5 atm之后则下降得比较快，当压力由0.2 atm降至0.1 atm时，比冲量值i1和i2迅速下降。

图5 比冲量随罐体内初始压力变化规律

2.3 压力波与比冲量无量纲化分析

图6 相对压力因子随罐体内初始压力变化

由图6、图7分别可以看出，相对压力因子α1和α2分别反映了罐体内第1个爆炸波和第2个爆炸波超压的衰减程度；同理，相对比冲量因子γ1和γ2分别反映了罐体内第1个爆炸波比冲量和第2个爆炸波比冲量的衰减程度，α和γ的值越大表明其衰减越快。当罐体内部初始压力降低至0.1 atm时：第1个超压波Δp1最高衰减达58.50%，第2个超压波Δp2最高衰减39.02%；第1个比冲量i1最高衰减85.65%，第2个比冲量i2最高衰减68.15%.

3 结论

本文自行设计一种φ320 mm×430 mm小型可抽真空柱形爆炸罐，进行了不同真空度下内爆实验，测试了工业雷管在不同真空度下的爆炸波超压、比冲量并且估算了爆炸波传播速度。得到主要结论如下：

1)爆炸罐内的气体介质密度会对爆炸波传播状态产生明显的影响。罐体气体介质密度降低时，爆炸产生的压力波和比冲量均会有所降低，在罐体内，爆炸波也更难产生叠加、反射，爆炸所带来的毁伤效果也会降低。

2)分别定义了相对超压因子α和相对比冲量因子γ来衡量爆炸波超压和比冲量的衰减程度，其值越大表明衰减程度越大。罐体内初始压力降低至0.1 atm时：第1个压力波Δp1最高衰减58.50%，第2个压力波Δp2最高衰减39.02%；第1个比冲量i1最高衰减85.65%，第2个比冲量i2最高衰减68.15%.

3)当罐体内部的初始压力低到一定程度时，其爆炸产生的能量会迅速衰减，此时能量的传播方式主要依靠爆炸产物。

4)爆炸波的传播速度会随着初始环境压力的改变而发生变化，初始环境压力越低，则其传播速度越快。