基于温度修正的弹丸挤进身管过程摩擦模型
邹利波,于存贵,冯广斌,侯保林,仲建林,刘宪福
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.中国船舶集团有限公司第713研究所,河南 郑州 450045)
0 引言
火炮发射时膛内的高温高压环境使铜质弹带承受了高强度冲击载荷与高速摩擦,尤其在弹丸挤进身管阶段,弹带被坡膛和膛线挤压剪切而逐渐挤入膛线。弹带与身管之间的接触摩擦规律不仅影响整个内弹道过程,而且对身管寿命以及寿命预测有一定的影响。
长期以来,诸多学者一直致力于揭示弹带与身管在膛内的接触摩擦规律,Montgomery[1-3]对高速高压摩擦做了大量试验研究,发现弹带材料与钢间的摩擦系数随着接触压力和相对滑移速度的增大而减小。美国陆军实验室[4]根据销-盘试验,将摩擦系数写为滑动速度与接触压力的乘积形式,其中每个因式中的参数通试验数据拟合。Matsuyama[5]基于弹带熔化机理,在一维非稳态传热基础上建立了弹带与身管之间的摩擦系数。Wu等[6-7]建立了模拟挤进装置,对弹带挤进身管的准静态以及动态挤进过程进行了试验研究,通过对比弹带的变形形态发现,在真实挤进过程中变形速度与温度对弹带变形形状有着重要影响。Ettles[8]认为弹带材料在滑动距离尚未达到一个弹带宽度时就已经发生熔化现象,对挤进过程摩擦现象进行研究后发现在火炮发射过程中,摩擦热要能够保证熔化层中材料熔化所需吸收的热能。Stiffler[9]根据流体动力学计算得到的弹带材料熔化液膜摩擦系数0.026较为相近。Puls等[10]利用高速切削实验对材料剪切过程中的摩擦现象进行了研究,采用一种以接触表面温度为变量的摩擦模型对实验过程进行了数值模拟。Shen等[11]在对弹丸在身管内运动进行数值计算时,认为弹丸与身管之间的摩擦系数保持不变。Ding等[12]研究磨损身管对内弹道的影响时,认为摩擦系数受温度影响,并给出了随温度变化的摩擦模型。Arnoux等[13]对高速摩擦现象进行了试验研究,得到了钢-钢之间摩擦系数的变化趋势,试验中的最大相对滑动速度可达80 m/s,正压力可达200 MPa;结合Sutter等[14]采用相同实验装置测得的滑块材料温度分布,认为随着接触压力的上升以及相对滑动速度的增加,局部剪切与材料熔化现象是导致摩擦系数缓慢下降的主要原因。List等[15]研究了高速高压下由摩擦引起的材料剪切行为。李明涛等[16]基于弹带熔化机理,假设带与身管之间存在一层薄膜润滑液,并建立了相应的摩擦模型。
本文在弹丸挤进身管过程中弹带变形机理基础上,结合前人研究成果提出一种新的摩擦模型,该模型反映了挤进过程中弹带的弹塑性变形以及在连续发射时弹带表层熔化,在弹带与身管之间形成一层液态膜;建立了弹带挤进身管的热力耦合有限元模型,对该摩擦模型进行了验证。
1 弹丸挤进过程中弹带变形机理
殷军辉等[17]对弹丸发射后的弹带硬度分布及组织演变规律做了详细研究,认为:弹带挤进身管的初期,温度略有升高但基本保持常温,可视为逐层发生剪切与挤压效应的冷塑性变形过程,强度和硬度均显著提高即产生加工硬化现象;随着挤进的深入,弹带径向过盈部分被膛线剪切而推挤到弹带后方或粘附在膛壁上,与阳线相对的多余材料被膛线剪切后,一部分被推挤到弹带后方,另一部分随接触面增大而逐渐挤入阴线并形成弹带侧壁表层的纤维组织。
弹带挤进后期,弹后空间火药燃烧产生的高温不断向坡膛和弹丸传递,再加上弹带变形量较大且与膛线的摩擦十分剧烈,因此弹带表层升温很快,在挤进完成后迅速超过其再结晶温度(紫铜仅为200~280 ℃,黄铜略高),弹带最外层的部分纤维组织历经回复、再结晶过程而演变为细晶组织(弹带表层出现的细小晶粒使这一推断得到证实)。由于塑性变形所引起的弹带表层硬化随弹带变形立即产生,而再结晶过程则需要持续一段时间才能完成,整个弹带挤进过程中发生的表层硬化并不能被其后的再结晶过程完全消除,最终形成细小晶粒区域内侧仍留有较厚的纤维组织即加工硬化层。
在连续射击环境下,火药燃烧及剧烈摩擦而使弹带表层承受了近千摄氏度的持续高温[18],导致弹带表层在进一步塑性变形的同时发生动态再结晶[17],从而使挤进初期形成的部分纤维组织因获得近乎稳定的流变应力而发生热软化甚至局部熔化。
2 摩擦模型
弹带材料为黄铜,身管材料为炮钢。挤进过程中的弹带变形机理直接影响弹带与身管之间的摩擦力。在高速高压摩擦中,较大的法向接触力使得摩擦表面间金属发生粘结摩擦[19-20]。根据粘结摩擦理论,剪断金属粘结点所需要的剪应力可以认为是摩擦力,故弹带与身管之间的摩擦力符合修正的库仑摩擦模型,其表达式如下:
τf=min(μ(T)p,τmax),
(1)
(2)
(3)
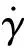
(1)式中的摩擦系数受温度、接触压力和滑动速率的影响。根据对弹带挤进过程中变形机理的分析,挤进过程中弹带与身管的摩擦系数变化可分为3个阶段:
第一阶段,挤进初期,弹带处于冷塑性变形,弹带与身管之间的滑动过程不受温度的影响,故弹带与身管之间的摩擦系数变化为常数,其值通过钢与铜摩擦副试验[21]获得。此时的摩擦系数可以用(4)式表示
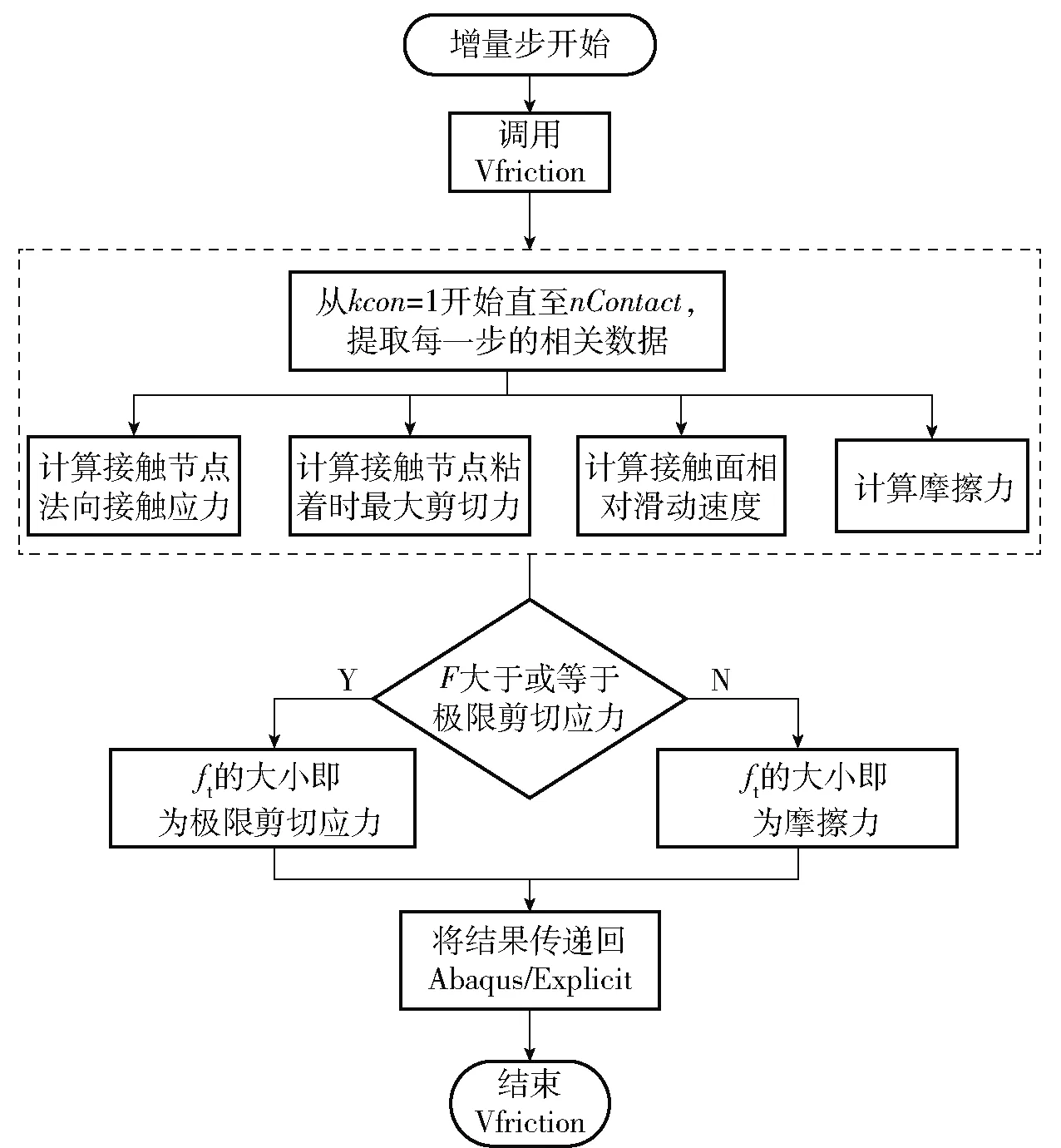
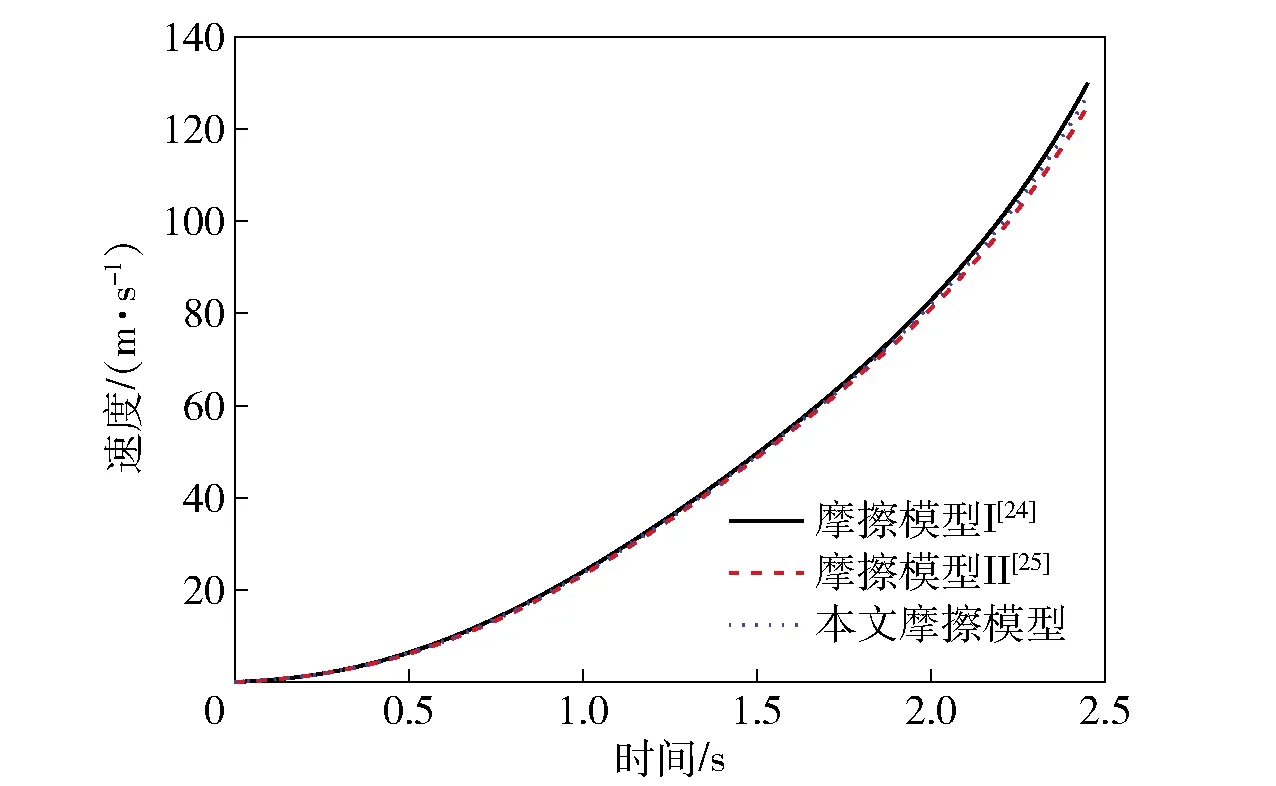
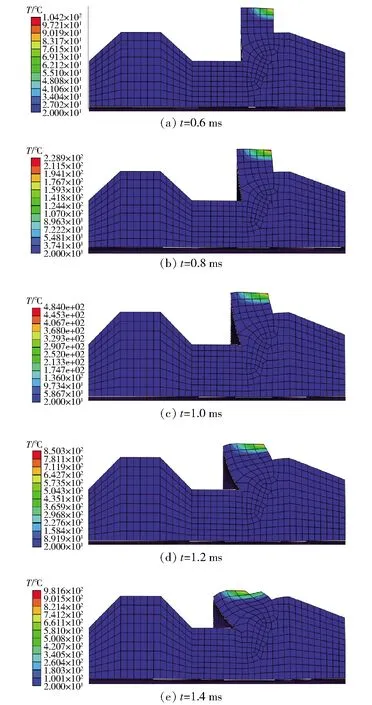
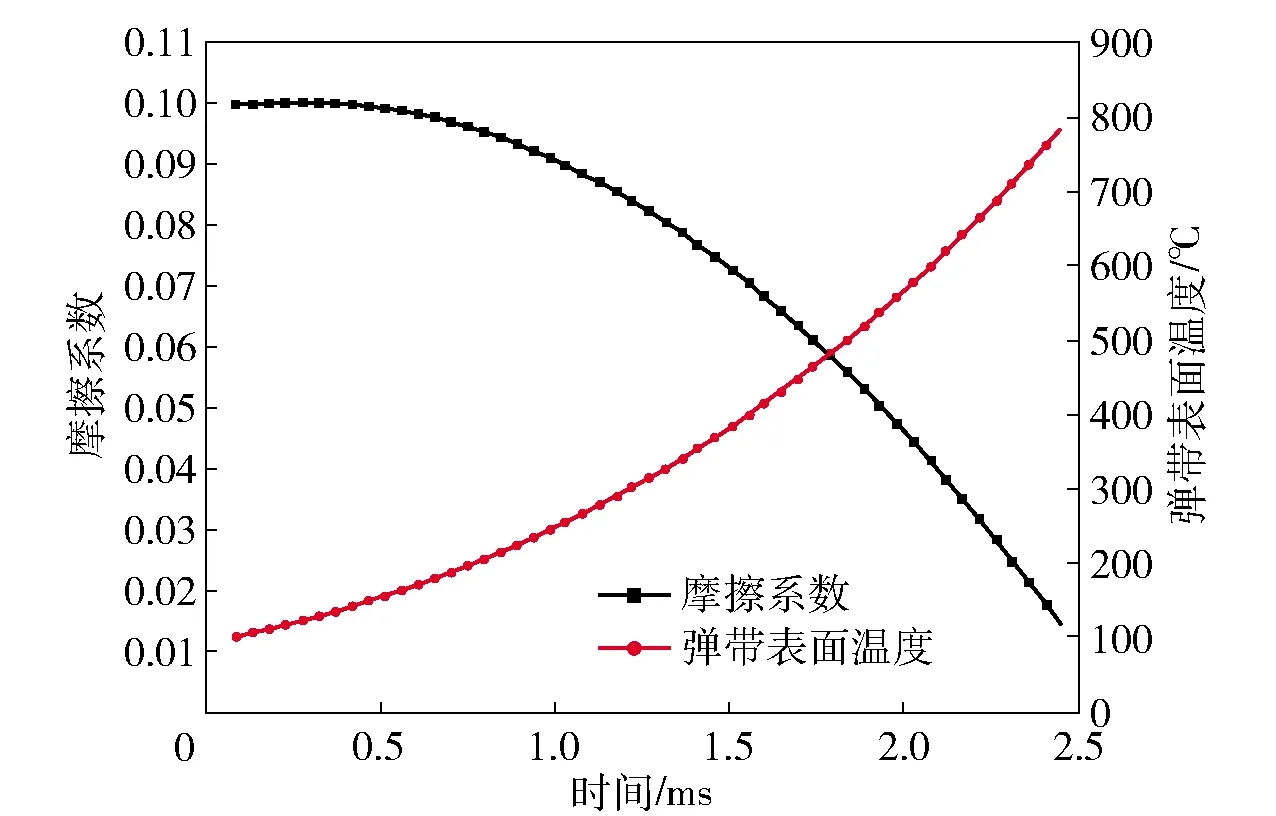
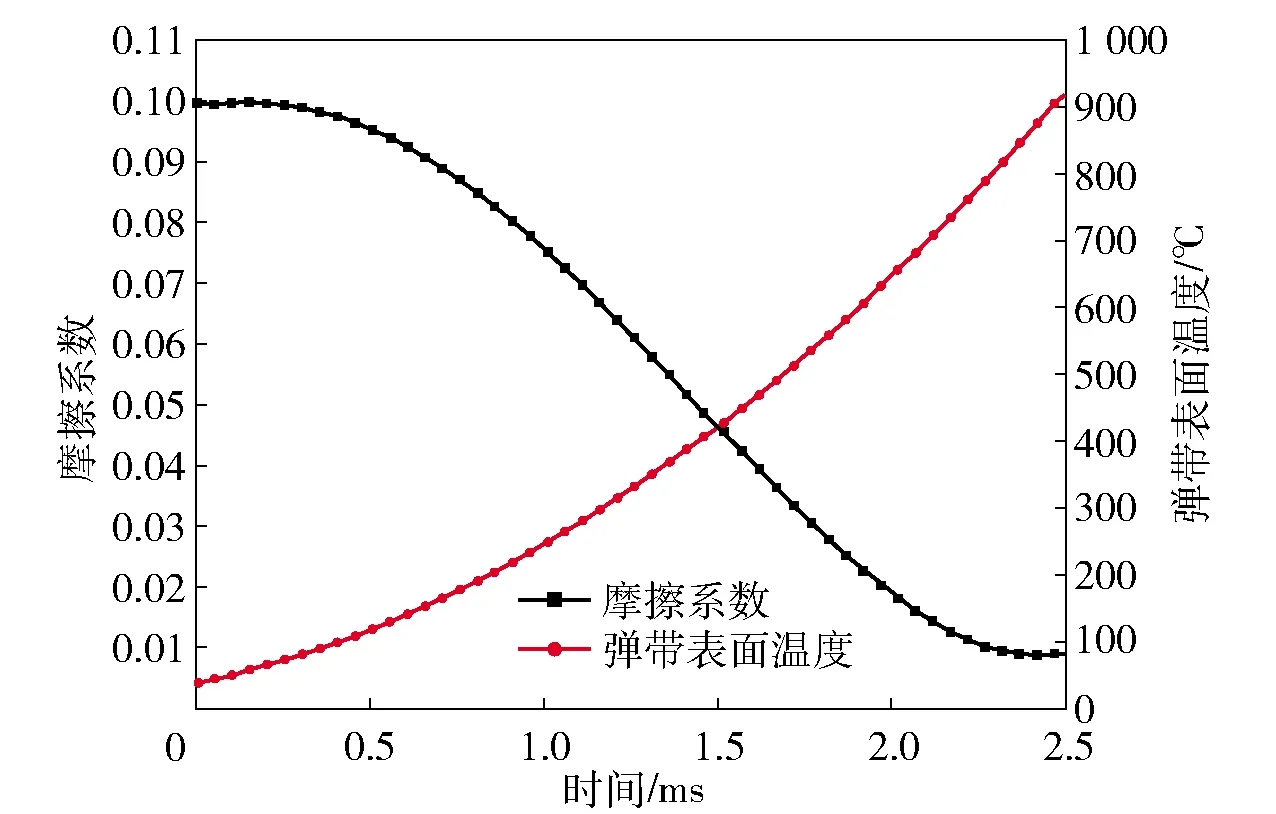
μ=μs=0.1,T (4) 式中:μs根据钢与铜的摩擦试验获得,取值为0.1;Td为弹带材料的再结晶温度。 第二阶段,随着温度上升,弹带表层组织发生再结晶现象,但未熔化。此时弹带开始软化,摩擦系数乘以一个温度软化系数[22],则该阶段的摩擦可表示为 (5) 式中:Tm为弹带表层熔化温度;mTSI为温度软化指数。 第三阶段,连续射击环境下,膛内温度不断升高,弹带开始熔化,在接触区产生很薄的熔化金属润滑膜。此时根据非稳态传热理论,考虑弹带与身管接触区域的总热流量为 Qtot=μpvs, (6) 式中:vs为滑移速度。 假设弹带表层熔化形成的液膜具有与弹带一样的热物性参数,当弹带表层熔化后其温度不再升高。结合非稳态传热理论,接触时弹带的热量为 (7) 式中:Ap=Hphp,Hp为弹带宽度,hp为弹带高度;λp为弹带导热系数;ap为弹带热扩散系数;λc为身管的导热系数;ts为弹带达到熔化时的时间;tu为弹丸挤进总时间;k为修正系数。 接触区域总的热量为 (8) 式中:tu为弹丸在膛内运动的时间;μm为弹带熔化后的摩擦系数。 身管的热量为 Qp=Qu,tot-Qc. (9) 当膛壁温度升到一定程度时弹带开始熔化,此时时间可表示为 (10) 弹带表层熔化后形成的熔化层热量为 Qp=hApρp(rp+cpTm), (11) 式中:h为熔化层厚度;ρp为弹带密度;rp为弹带材料熔化热;cp为弹带比热容。 从而可推导出熔化层厚度为 (12) (7)式、(8)式代入(12)式,即可得到(13)式: (13) 综上所述,弹带挤进时期的摩擦模型可以表示为 (14) 式中:F为切向摩擦力;σn为法向接触压力;Fn为法向作用力。 挤进过程中,在粘结滑移区以及纯粘结区中,弹带接触表面材料存在较大的速度梯度,表面金属产生大应变率变形,塑性功转变为热能,同时弹带表面与身管的高速摩擦也产生大量的摩擦热。三维非稳态、变物性的热传导微分方程为 (15) Q=Qp+Qf+Qh, (16) 式中:ρ、c表示材料的密度和比热容;kx、ky、kz分别为x轴、y轴、z轴3个坐标轴方向的热传导系数;Q为内热源;Qf为接触界面的摩擦热;Qh为内膛火药燃气与身管表面的对流交换的热量。 弹丸在挤进过程中经历弹塑性变形及损伤,最终发生局部化韧性断裂,涉及到弹带材料的应变硬化、应变率硬化和温度软化,Johnson-Cook本构模型适合描述大部分金属材料[23],故采用Johnson-Cook本构模型及其失效本构模型,其表达式分别为 (17) (18) =(T-Tr)/(Tm-Tr), (19) 表1 弹带的Johnson-Cook材料模型参数 表2 炮钢的Johnson-Cook材料模型参数 表3 弹带和炮钢材料的热物理参数 在火炮射击过程中,膛内火药燃气的强制对流作用,使火药燃烧释放的热量穿过热边界层逐渐传递到身管,通过热传导不断将热量传递到外壁,外壁温度逐渐升高;然后通过自然对流的方式使热量逐渐被环境气流带走。膛内高温火药气体与膛壁之间存在温度差,因此必然发生热量交换。由于舰炮连续射击过程中的射击间隔相对较短暂,假设弹丸挤进前坡膛表面已受到火药燃烧产生热量。此时身管主要受到三部分热量:1)火药气体以强迫对流换热的形式直接作用在坡膛表面的热量;2)外壁面受到冷却水对流换热产生的热量;3)弹带挤进膛线的过程中,由于塑性变形导致不断出现的新生面与身管膛面剧烈摩擦,摩擦功最终表现为热量的释放。在以上分析基础上,建立发射时身管的初始条件和边界条件如下。 初始条件:t=0 s,T=Ta,Ta为环境温度; 内、外边界条件:t>0,身管内表面边界条件为 (20) 身管外表面边界条件为 (21) 式中:λ为身管材料的导热系数;ri为身管内径;ro为身管外径;hg为火药气体与身管内表面的换热系数;Tg为火药燃气温度;he为周围空气与燃烧室本体外表面的对流换热系数;Te为环境温度。弹丸发射过程中,火药气体沿身管轴向流动的方式是带热体的紊流流动,这种流动方式的显著特点是强烈的漩涡运动,因此形成身管壁与火药气体热交换的主要形式为强迫对流换热。为简化求解问题,现假定只存在强迫对流换热,当求出放热系数后再针对辐射换热作适当的修正。火药燃气的放热系数根据相似理论计算[18-19]: Nu=0.023Re0.8Pr0.8, (22) 式中:Nu为努赛尔数;kg为气体特征数;Re为雷诺数;Pr为普朗特数。由(22)式可得 (23) 式中:T∞为身管外壁温度。 弹丸底部施加弹底压力,弹底压力根据三基混合装药内弹道方程组计算获得,其方程如(24)式所示: (24) 式中:φ为相对已燃体积;Z为火药燃烧量;u1为燃速系数;e1为药弧厚度;pg为膛内火药气体压力;n为燃烧指数;mp为弹丸质量;v为弹丸速度;S为身管的横截面积;f为火药力;k0为绝热系数;φ为忽略挤进阻力的次要功系数;lφ为药室自由容积缩径长;l为弹丸行程;l0为药室容积缩径长;Δ为装药的装填密度;ρm为混合装药密度;a为发射药的余容。 弹丸挤进身管坡膛过程中,弹带与身管之间接触的摩擦模型采用本文提出的模型,并通过有限元软件子程序VFRIC实现,在程序中通过计算单元节点切向力ft来输出摩擦力的值,其实现流程如图1所示。 图1 摩擦计算流程 以某中口径舰炮身管为研究对象,从完整身管中截取身管坡膛的起始部结构,分别建立该部分和弹丸的有限元网格模型,并采用C3D8RT单元对其划分网格。在有限元模型中,弹带与弹体采用节点绑定的方式模拟弹带与弹体的装配关系;弹带、弹体定心部与坡膛内表面接触设置;装药质量以质量点的形式均匀耦合在弹丸内表面。由于弹带切入膛线过程中弹带内部单元网格会暴露出来与坡膛内表面接触,故弹带采用自接触设置。图2所示为身管坡膛起始部详细结构的有限元网格模型,图3所示为装配后的弹炮耦合有限元网格模型。其中,身管坡膛结构网格模型单元个数为176 262,节点个数为205 920. 图2 身管坡膛结构有限元网格模型 图3 弹丸-身管耦合作用有限元模型(剖视图) 为了验证本文所提摩擦模型的正确性,将本文提出的模型与文献[24]、文献[25]研究的摩擦模型(分别记为摩擦模型Ⅰ和摩擦模型Ⅱ)进行对比。摩擦模型Ⅰ是通过对弹带材料在真空销-盘摩擦试验机上高速高压摩擦测得的数据进行拟合得到的摩擦系数表达式,摩擦力仅与正压力和相对滑移速度有关,如(25)式所示。摩擦模型Ⅱ[25]是基于流体动力润滑理论,假设弹带熔化成不可压缩流体的基础上所建立的挤进过程身管摩擦模型,如(26)式所示。 (25) F=min(μσn,τs); (26) 式中:a1和b1为材料模型参数。 将摩擦模型Ⅰ[24]和摩擦模型Ⅱ[25]通过子程序接入热力耦合弹炮匹配有限元模型中,分别获得单发射击时挤进过程中的弹丸质心速度,如图4所示。 图4 弹丸质心轴向速度 由图4可以看出,3种摩擦模型耦合计算得到的弹丸质心轴向速度规律相符合,挤进完后弹丸质心轴向速度约为129 m/s.图5(a)、图5(b)和图5(c)分别为挤进过程中的弹丸质心在轴向方向、水平方向和竖直方向的加速度随时间变化曲线,从曲线可知:3种摩擦模型耦合计算得到的弹丸质心在3个方向上的加速度幅值大小和规律基本一致。 图5 弹丸挤进过程中弹丸加速度参量变化 图6所示为采用本文所提摩擦模型计算得到挤进过程中的弹底压力和弹丸挤进阻力。由图6(a)可见,完全挤进后弹带加速度达到了270.75 MPa,通过试验测试在相同时刻的弹底压力约为262.9 MPa左右,计算值与试验值误差较小。从图6(b)可以看出,在1.8 ms时刻左右弹丸挤进阻力最大值约为145 152 N,与实际情况符合。由此可知,本文所提基于温度修正的挤进过程摩擦模型具有一定的可信度。采用摩擦模型Ⅰ[24]计算得到的挤进速度偏大,可能原因在于该模型是对“销-盘”摩擦试验数据的拟合得到的,未考虑弹带受温度软化的影响。摩擦模型Ⅱ[25]是以弹带与身管之间的边界温度为分界点判断弹带的软化对摩擦的影响,且根据流体动力润滑理论描述弹带表层熔化后的摩擦特性,熔化液膜的运动特性对模型的影响较大,而且计算过程较为复杂。由此可见,本文提出的摩擦模型具有一定的可信度。 图6 弹丸挤进过程中弹丸受力特性 从弹带挤进过程中应力云图变化的剖视图来看,挤进初期,弹带凸缘处开始于身管接触,由于法向压力较小,温度较低,弹带与身管之间为滑动摩擦,弹带材料逐层发生挤压和塑性变形,如图7(a)和图7(b)所示;随着挤进的深入,温度升高,弹带凸缘部分发生局部剪切现象,温度对弹带与身管之间的摩擦有一定的影响,如图7(c)和图7(d)所示,此时的弹带局部von Mises应力约为546.7 MPa;最后,弹带径向的过盈部分受膛线剪切被推挤到弹带后方,与阳线相对的弹带材料被膛线挤压和剪切后,一部分被推挤到弹带后方,另一部分逐渐挤入阴线。 图8所示为弹带挤进过程中弹带温度变化云图。由图8可以看出,整个挤进过程只有与身管接触的弹带表层温度变化较为明显,原因在于挤进过程时间及其短暂,温度来不及扩散,大部分温度聚集在弹带表层,弹带完全刻槽后表层温度达到了981.6 ℃,如图8(e)所示。这种现象与第1节中挤进过程中弹带变形机理描述相一致。 图8 挤进过程中弹带表层温度变化云图 在以上研究的基础上,进一步获得单发射击和连续射击条件下弹丸挤进过程中弹带与身管之间摩擦系数的值。连发射击时,采用射击规范为:射频为130 发/min,环境温度为293 K,冷却水流速1.5 m/s,正装药。需要说明的是,射频130 发/min为研究对象的最高射频,实际射击时低于此值。如图9所示,在单发挤进过程中,随着挤进的不断深入,弹带表面温度升高,弹带与身管之间的摩擦系数逐渐降低,当弹带表面温度达到789 ℃时,摩擦系数为0.014.在连发挤进过程中,由于弹带在外界热源不断输入情况下,弹带表面摩擦系数温度迅速升高,当连续射击第2发时弹带开始刻槽时刻,弹带达到熔点温度,弹带与身管之间形成一层“润滑膜”,此时的摩擦系数为0.008 6,且随着连发次数的增多,弹带与身管之间的摩擦系数一直维持在这个值左右,如图10所示。 图9 单发射击时摩擦系数 图10 第2连发射击时摩擦系数 本文结合挤进过程中弹带变形机理,提出一种适合描述弹带与身管之间相互作用的摩擦模型,该摩擦模型主要受弹丸挤进过程中弹带与身管之间温度软化的影响。在热力耦合的弹炮相互作用有限元模型基础上对该模型进行了验证。得到以下主要结论: 1)通过数值计算,获得弹丸挤进过程中的弹丸质心轴向速度和3个坐标轴方向的加速度,与现有研究的摩擦模型计算对比,其规律和幅值大小基本一致,故本文提出的摩擦模型具有一定的可信度。 2)在该模型基础上,获得了弹丸挤进过程中弹底压力和弹丸挤进阻力变化曲线,与试验值基本一致。 3)在该模型基础上,获得了单次挤进和连续挤进过程中,弹带与身管坡膛之间的摩擦系数随温度变化规律。 4)该摩擦模型的提出为弹炮匹配计算提供一种新的输入,同时为计算身管坡膛的磨损提供一定的理论基础。
3 弹丸挤进过程中的热力耦合模型
3.1 传热模型
3.2 材料模型
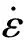



3.3 边界条件

3.4 载荷施加
3.5 摩擦模型
4 弹丸挤进过程有限元模型建立与验证



5 结果分析
5.1 弹丸挤进过程中弹丸运动规律


5.2 弹丸挤进过程中弹带应力变化
5.3 挤进过程中弹带温度变化
5.4 摩擦系数变化
6 结论

