大型隔膜泵进料阀箱紧固导管三维流固耦合分析

齐东杰，李文明，陈 扬，2，张恩龙

（1.中国有色（沈阳）泵业有限公司，辽宁沈阳 110144；2.沈阳工业大学 材料科学与工程学院，辽宁沈阳 110870）

1 模型与边界条件

两种不同结构的紧固导管三维模型图如图1所示，分别为两流道和四流道。其中，流道截面尺寸为30mm×15mm。对两种结构阀箱的几何模型进行简化并采用专业前处理软件进行网格划分，网格均为六面体单元。两种结构进料阀的流体与结构部分网格如图2所示。

图1 两种紧固导管的三维结构图

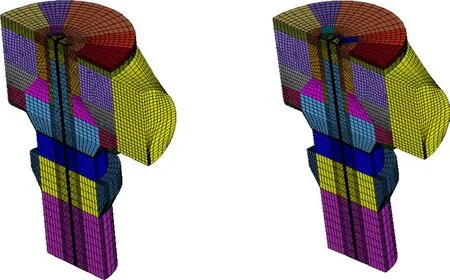
图2 两种结构进料阀内部流场与结构网格

流体部分边界条件与载荷如下：紧固导管内流体下表面为流固耦合边界，紧固导管与流体无相对滑移部分为流固耦合边界，阀体（除导杆部分）与流体部分为流固耦合边界；整个流体边界为固定墙；紧固导管内流体与导管有相对滑移部分为滑移墙，阀导杆与流体部分为滑移墙，流体整个对称面为滑移墙；进料阀进口面定义输流速（流速按照从0时刻起至0.67s按正比例函数定义，最大流速为2.65m/s）；阀与流体之间间隙部分定义为GAP边界条件，GAP根据尺寸进行设定（阀的开启与关闭尺寸分别为1 703.5和1 703.2）。

结构部分边界条件如下：结构部分的流固耦合边界与流体部分对应；在阀上表面上方30mm位置建立一几何面以限制阀的升程，该几何面与阀体上表面所形成的单元面集之间定义接触对（几何面为目标面、阀上表面为接触面）；限制阀体自由度只有竖直方向运动，对紧固导管上表面定义全约束。

两种结构的进料阀内腔流体和结构模型导入ADINA后如图3所示。

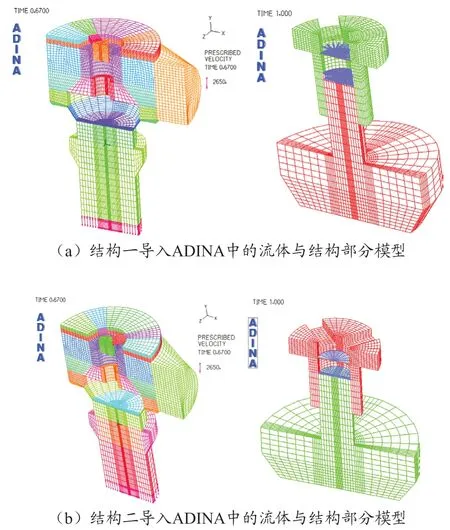
图3 两种结构进料阀内部流场与结构导入ADINA示意图

2 计算结果

在给定的工况下，经ANINA流固耦合计算分析，经0.21s后阀达到最大升程30mm。分别分析两种结构在阀达到最大升程以及之后紧固导管内的流速变化情况。下面提到的单流道即为结构一模型，双流道即为结构二模型。

图4为时间为0.21s时单流道单流道流场速度云图和速度矢量图，最大速度位于流道出口处，速度方向指向流道外侧。图5与图6为时间为0.67s时流场速度云图和速度矢量图，图中可以看出速度最大值位于流道出口处，最大速度为820mm/s，而在流道内和紧固导管内的流体速度均非常小，即紧固导管内流场趋近于静止。

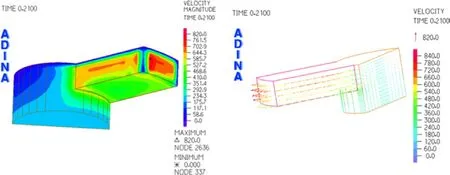
图4 单流道流场速度云图和速度矢量图（t=0.21s）

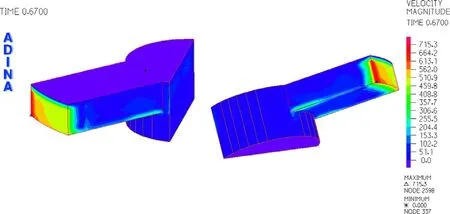
图5 单流道流场速度云图（t=0.67s）

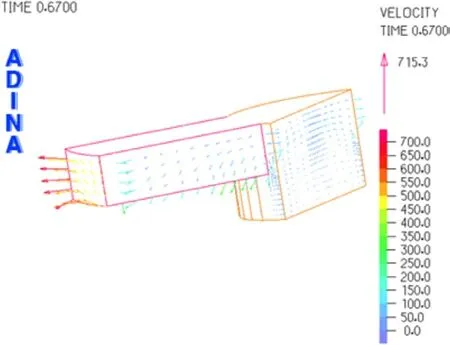
图6 单流道流场速度矢量图（t=0.67s）

图7为时间为0.21s时双流道单流道流场速度云图和速度矢量图，相比于单流道，双流道的最大速度较小，其值为621.2mm/s，位于其中一条流道出口处。而另一条流道流速非常小。图8时间为0.22s时双流道速度矢量图，从图8中可以看出流速减小，右侧流道流速方向开始转向。

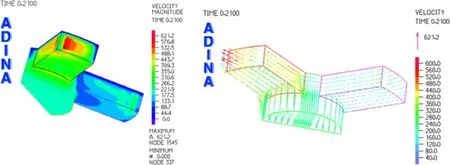
图7 双流道流场速度云图和速度矢量图（t=0.21s）

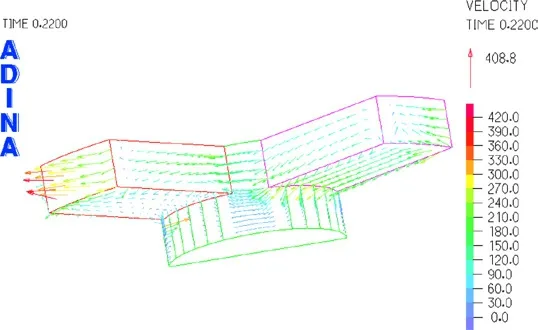
图8 双流道流场速度矢量图（t=0.22s）

图9 为时间到达0.67s时双流道流场速度云图与速度矢量图，最大速度已经达到1 128mm/s，位于左侧流道出口处与右侧流道转角处。从中可以得出，当阀达到最大升程后，两条流道形成一条通流流道，且流速非常大。

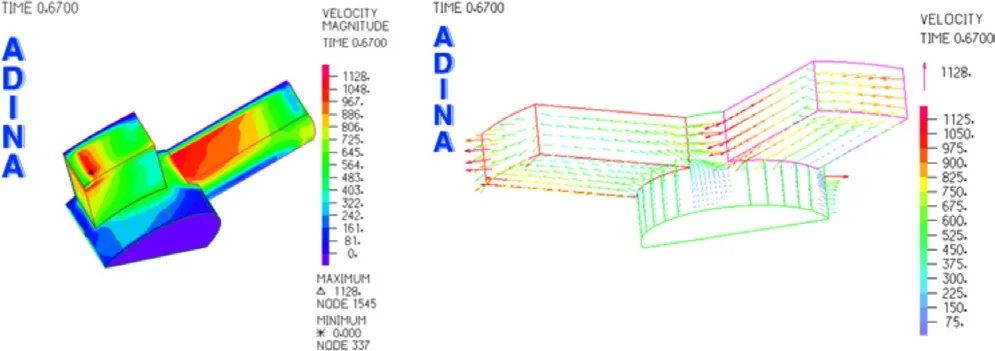
图9 双流道流场速度云图和速度矢量图（t=0.67s）

分别取单流道与双流道转角处较大速度的一点，提取其整个过程中的流速，绘制成如图10所示。从图10可以看出，阀上升过程中单流道的流速相对较大，当阀达到最大升程后，单流道的速度迅速下降。而双流道自阀达到最大升程后，其速度经过略微下降后，开始迅速上升。

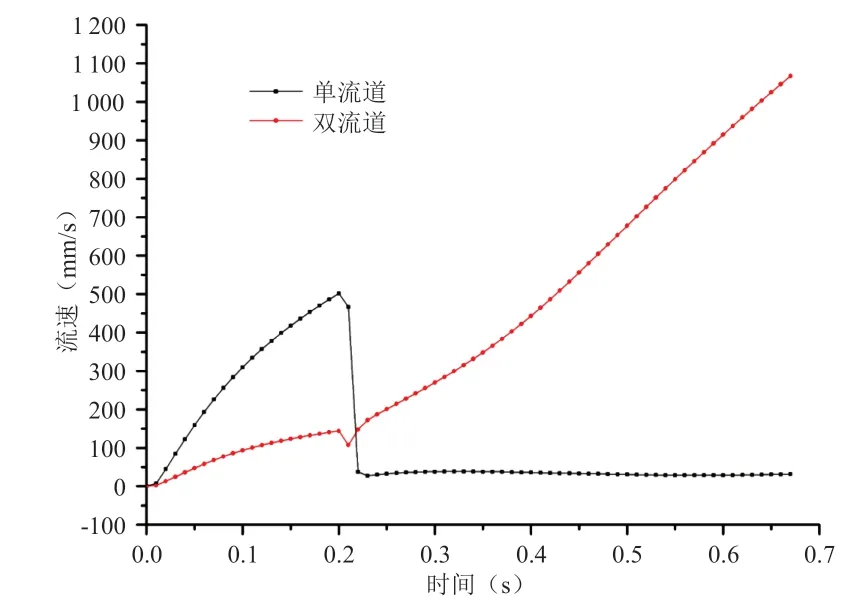
图10 两种结构流道转角处的流速曲线图

3 结论

1）阀上升过程中单流道的流速相对较大，而双流道相比于单流道可以缓解阀上升过程中紧固导管的磨蚀。

2）当阀达到最大升程后，单流道内速度迅速减小，紧固导管内流体几乎处于静止状态；而双流道结构会在两条流道内形成通流，而且其流动时间较长，流速较大，会对紧固导管造成较严重磨蚀。综合考虑，单流道较有利于紧固导管的使用。