基于改进因子图模型的航天器组合姿态确定算法
华 冰, 梁莹莹, 倪 瑞
(南京航空航天大学航天学院, 江苏 南京 211000)
0 引 言
航天器的姿态确定指航天器依靠自身携带的敏感器的测量信息或者其他信息,通过数据处理获得航天器本身相对于某一坐标系姿态参数的过程[1],姿态确定的精度会直接影响航天器整体的控制和导航精度[2],是航天器在轨平稳运行、完成多种任务的关键。
目前小卫星常用姿态敏感器包括磁强计、红外地平仪、星敏感器、太阳敏感器、陀螺等,单个传感器运用姿态确定往往缺乏足够的稳定性和可靠性,精度也不高,因此一般采用组合测姿方法进行姿态确定。如:星敏和陀螺姿态确定[3]、星敏与红外地平仪进行组合测姿[4]、采用分布式融合方式进行组合测姿[5]。传统的组合姿态确定常采用联邦滤波的形式,将各个传感器作为子滤波,分布式计算,然后分配权值进行融合,该方法结构简单,具有计算量小,精度较高等优点。在实际任务中,通常各个传感器的更新频率不一致,因此往往需要进行数据同步处理,而上述传统方法容易造成数据浪费;同时,若某一传感器失效,需要增加或者替换新的传感器时,则需要复杂的系统重构。
因子图[6-7]是图模型中的一种,用于表示函数的因式分解,其在统计推断、译码编码、消息传递、滤波平滑等方面都有所应用。目前在一些小型场景中机器人的定位导航与建图[8-9]中有广泛的运用。Kschischang[10]最早提出了因子图的基本概念并总结了因子图和积算法,给出了详细的数学理论过程;由于其强大的包容性,常被用于解决不同场景下的多源导航传感器融合问题,如Chiu等[11]在美国Georgia理工学院的研究基础上,将因子图模型用于包含57种不同的传感器的机器人自主导航问题;德国Lange[12]等将基于因子图模型应用到装配有惯性测量单元、光流传感器和无线电高度表的四旋翼无人机中;因子图模型也被用于航天领域,Tweddle[13]等建立了空间非合作目标刚体动力学因子图,用于估计和预测非合作目标的各种状态参数;Takeishi等将因子图应用在小行星探测背景[14-15]中;因子图在水下航行器[16]、无人机[17]、室内机器人[18]、航天器上都有广泛的应用,基于因子图的惯性/视觉信息融合方法是因子图算法一大方向,国内也将因子图用于组合导航[19]、检验失效航天器[20]、航天器故障诊断[21]、姿态估计[22]、室内导航等。
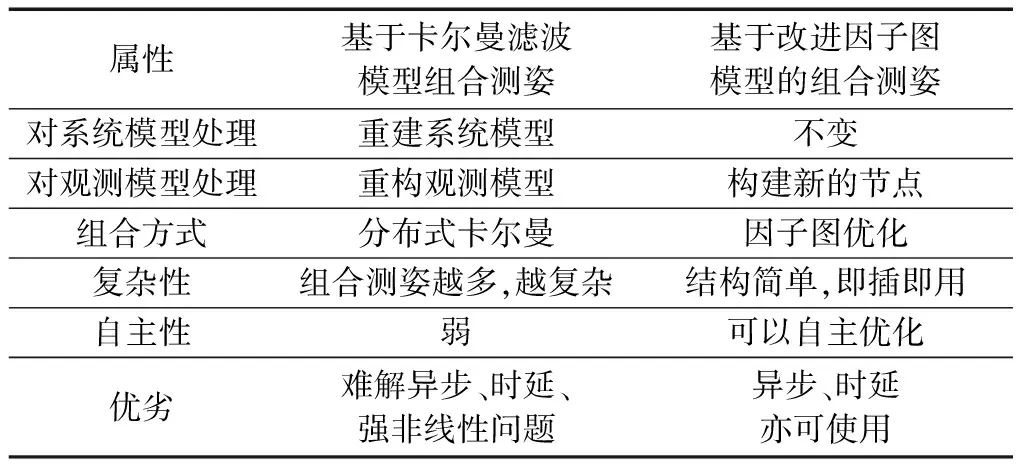
卡尔曼滤波是组合定姿中常用的方法。该方法通过计算卡尔曼增益,仅使用上一时刻状态进行实时的状态估计[23],其姿态确定的精度依赖于模型的准确度,适用于线性系统,难以应对复杂多变的情况,缺乏自主优化手段;相比于卡尔曼滤波,基于因子图模型的方法可以通过图优化保留过去的状态,当新的信息引入之后,对过去的信息一起进行优化[24]。另外,由于各传感器的工作频率不同,基于卡尔曼滤波的姿态确定算法在进行多传感器融合的数据同步时,会造成数据浪费;另一方面,当出现传感器的增减、或者出现失效传感器的时候,由于各传感器间的误差特性不同和测量误差非高斯分布等特点,基于卡尔曼滤波的算法需要重新进行复杂的系统重构,这会大幅增加系统设计的复杂性,不利于新算法的拓展和多传感器的使用。因子图模型在复杂环境中有较好的表现力,传感器的增删可以方便地通过传感器因子的增删实现,从而合理而充分地利用其他姿态测量信息实现即插即用,避免了复杂的系统重构,具有较好的包容性和易扩展性,为实现高精度、鲁棒性强的自主导航技术奠定了基础。
本文提出一种基于改进因子图模型的航天器组合姿态确定方法,针对典型的航天器姿态确定系统,通过建立因子图模型,将多传感器测量信息作为因子节点,即插即用地加入因子图模型。针对多测量信息频率不一致、存在数据冗余和误差不一等问题,该方法对多源观测数据集进行了观测蒸馏,通过提炼出高质量的观测值实现增量化构建因子节点,对基于因子图进行完善;然后通过自适应调整观测数据权值降低数据量,同时分析了观测数据对整体姿态确定精度的影响,并筛除其中的不利观测数据,从而提高航天器的姿态确定精度。
1 典型地磁/星敏/陀螺姿态确定系统
星敏感器是常用的姿态确定敏感器,精度高,但更新频率低;磁强计性价比高、稳定性强、更新频率也较高,但是精度较低;陀螺通过积分可以测量姿态的角速度,但长时间会存在较大的累计误差。星敏与陀螺组合可以弥补星敏频率低的缺点,但是一旦星敏故障,则无法保证精度。多传感器组合姿态确定的方法常采用联邦滤波的方式,如图1所示。该方法需要进行数据同步,而此过程中往往更新频率取决于星敏感器,因此通常会造成一定的数据浪费。当需要加入新的传感器时,则需要重新设计系统构型。本节将对典型的姿态传感器模型进行介绍,该部分也是进行建立传感器因子节点的基础。

图1 典型地磁/星敏/陀螺姿态确定系统结构图
1.1 测量模型
1.1.1 磁强计测量模型
对于近地航天器,在外部磁场影响可忽略的情况下,可以采用高斯球谐函数将地磁场势函数描述为
V=
(1)
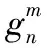
地磁场强度矢量可以表示成地磁场势函数的负梯度,在地理坐标系中,为磁场V在北、东、地3个方向的分量,由此可以得到地磁场矢量与航天器所在位置的关系式,即地球固联坐标系e中地磁场矢量:
(2)
式中:Be=[Bex,Bey,Bez]表示航天器地理系三轴磁场矢量;将本体系三轴磁场矢量小量作为观测量[25],可以表示为
Z1=ΔBb=A(Q)δQ+A(Q)ΔB0+v1
(3)
式中:B0=Aoi(orbit)Be,Aoi表示轨道系到惯性系的转换矩阵,与航天器位置orbit相关;v1为测量误差;A(Q)为轨道系到本体系姿态转换矩阵;Bo,Bb为航天器轨道系、本体系的三轴磁场矢量,具体转换方式同方法[23]。
1.1.2 星敏感器测量模型
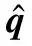
(4)
选取观测量为测量误差四元数矢量部分:
Z2=Csδqs+ν2
(5)
式中:Cs=diag{1+μ,1+μ,1+μ},μ是均值为μμ的白噪声;ν2为测量误差,是均值为0的白噪声。
1.1.3 陀螺测量模型
陀螺是卫星姿态控制系统中一种极为重要的敏感器,其输出卫星三轴相对于惯性空间的角速率,与姿态敏感器联合使用进行姿态确定,可以实现对姿态角速度的测量,输出相对于参考坐标系的角速度,不考虑安装误差和陀螺指数漂移,其测量模型如下所示:
ωg=ω+b+ηg
(6)
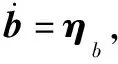
1.2 姿态运动学模型
用姿态四元数来对航天器的姿态运动进行描述,可以表示为
(7)
式中:Q=[q0,q]表示姿态四元数,q0为姿态四元数标量部分,q为矢量部分;ω=[ωx,ωy,ωz]为姿态角速度;ω×表示向量的叉乘反对称阵。对式(7)进行求导,并忽略二阶小量可得
(8)
由于四元数存在奇异的问题,针对小角度的机动的航天器,采用误差四元数对姿态进行动态描述,可以有效避免该问题。航天器在外力矩的作用下,发生姿态的改变。外力矩一般包括航天器的控制力矩与空间扰动力矩。姿态动力学方程用于描述转动角速度和所受外力矩之间的关系,即
(9)
式中:J为航天器的转动惯性量;h为动量轮角动量;Nτ为空间扰动力矩;Nr为控制力矩。不考虑角动量轮的作用,空间扰动力矩,控制力矩均为0情况下,进行求导得
(10)
2 基于改进因子图模型的航天器组合姿态确定算法
航天器的姿态运动是一个典型的马尔可夫过程,是一个多变量控制系统。如果采用因子图模型建模,状态的传递,以及姿态的观测,可以非常方便地通过作为因子变量的方式加入到模型之中[27]。在因子图模型中,变量节点到因子节点或者因子节点到变量节点的是通过信息交互的,因此节点的变化和增删可以很灵活地通过信息传递反应,从而实现传感器的即插即用。
一般线性系统的因子图表示如图2所示。其中,方块表示函数关系;圆圈表示状态量。状态通过类似马尔可夫链进行传递。
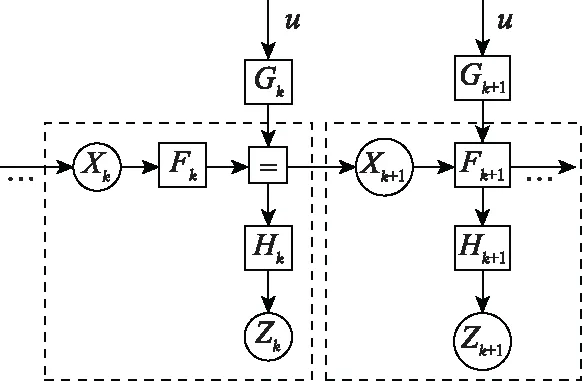
图2 一般线性系统的因子图表示
考虑航天器稳定时期的姿态运动为小角度运动,常用姿态四元数描述航天器姿态运动,误差四元数的动态变化可以直接反应航天器姿态变化,基于因子图的航天器姿态运动模型利用误差四元数传递姿态变化,然后通过四元数计算得到航天器的最后估计姿态,可简化表示为图3所示。

图3 基于因子图的航天器姿态运动模型
由于传感器制造工艺、使用环境、精度大小以及本身观测方式的不同,不同传感器获取的姿态信息质量不一,基于改进因子图模型的航天器多传感器组合姿态确定算法的基本思想是:利用先验信息,采用观测蒸馏法,计算观测残差,对观测数据集进行提炼,同时对提炼的信息进行自适应调整,将调整的观测量作为节点增量更新因子图,构建滑动窗口的航天器姿态因子图状态模型[28],从而高效合理利用多传感器信息,提高整个系统的精度。系统整体如图4所示。
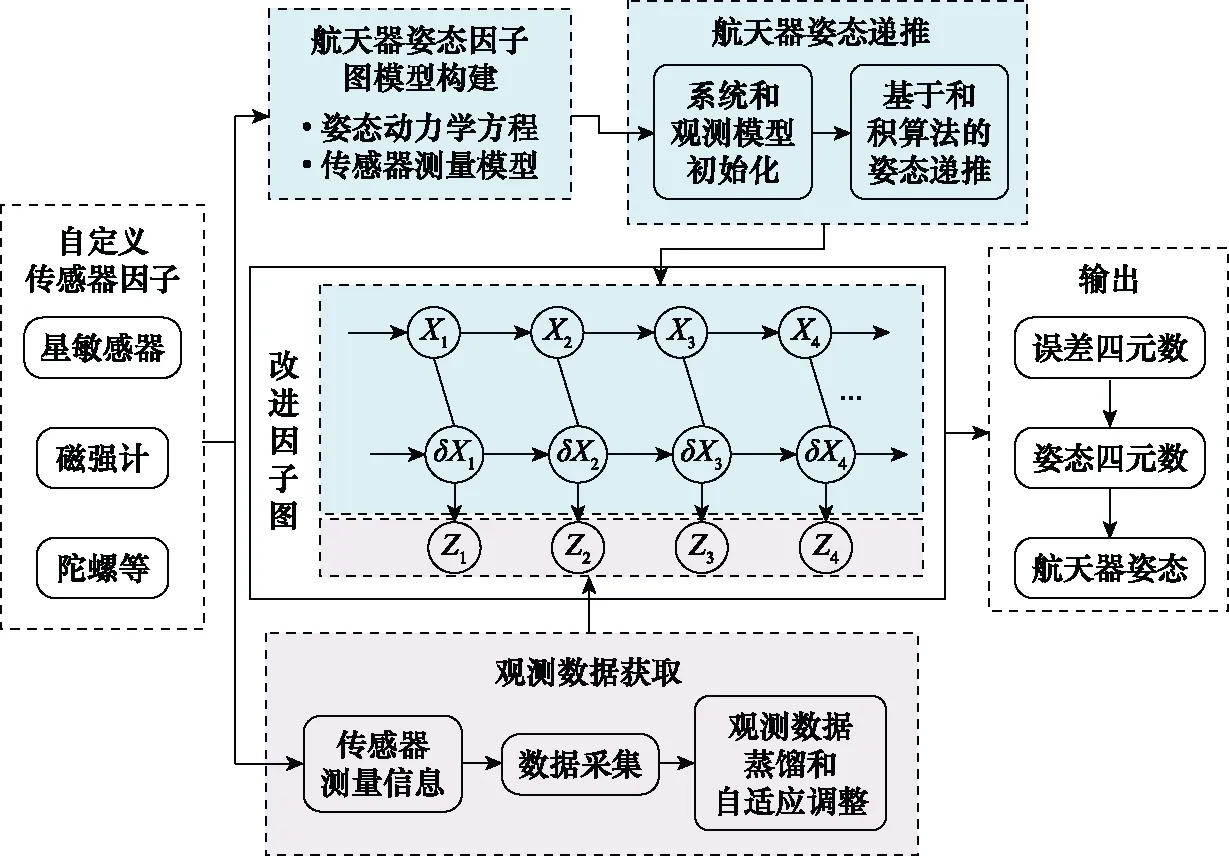
图4 基于改进因子图模型的航天器多传感器组合姿态确定算法结构图
接下来对算法进行具体介绍:算法的核心在于构建某一时间段内的因子图模型,将系统状态与姿态测量信息相关联,再基于后验估计理论实现数据的融合[29]。即在给定所有可用量测值后,计算所有状态的联合概率分布函数的最大后验概率估计,其计算方法如下所示:
(11)
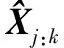
P(Zi|Xi)P(Xi|Xi-1)
(12)
根据最大后验概率的公式和全概率贝叶斯公式,求解满足最大后验概率最大的状态变为最终的估计值,则一段时间tj时刻到tk时刻之内的后验概率可以表示为
(13)
式中:P(Zj:k|Xj:k)表示tj时刻到tk时刻之间的ti时刻的观测量相对于ti时刻的状态量Xj:k的先验概率;P(Xj:k|Xj:k)表示ti时刻的状态量Xj:k相对于前一时刻状态量的先验概率。
通过式(13)可看出,该先验概率可以表示为多个函数相乘的形式,表示为如下形式:
(14)
2.1 姿态测量信息因子
在卫星姿态确定系统之中,传感器的测量模型一般为线性模型,可以表示为
Zi=hi(Xi)+Vi
(15)
式中:hi(·)表示传感器的测量函数,给定估计状态可以通过测量函数得到传感器的预测值;Vi表示为均值为0的白噪声。把误差函数描述为传感器的实际测量值与预测值误差,即err=Zi-hi(Xi)。其中,Zi表示实测值,定义传感器因子节点f(Xi)为ti时刻每个观测量相对于状态量Xi的误差函数,因子节点fi与误差函数err(Xi,Zi)有关,可表示为
f(Xi)=d[err(Xi,Zi)]
(16)
式中:d(·)表示对应的代价函数。
针对第1.1节中不同传感器的从测量模型,磁强计因子节点可以具体表示为
(17)
星敏感器因子节点可以表示为
(18)
对于高斯分布,式(18)的代价函数可以表示为指数形式,即
(19)
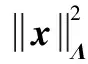
2.2 航天器姿态运动学因子
航天器姿态运动学因子节点函数可表示为
err(Xi,Xi-1)=g(Xi-1)-Xi
(20)
式中:g(·)为状态转移函数。由于状态量的转移满足姿态动力学方程,如第1.2节所述。同样,概率密度P(Xi|Xi-1)可以表示为指数形式:
(21)
(22)
式中:Xi-1和Xi表示为ti时刻状态和前一时刻态。
2.3 改进因子图模型的航天器组合姿态确定算法
利用建立的传感器因子节点和姿态动力学因子节点,带入并对式(12)左右取对数,从而将乘积变成和的形式,将式(14)实际上变成了一个优化问题。
(23)
因此,基于改进因子图模型的多传感器姿态确定的过程可以描述为:在已知所有观测量Zj,Zj+1,…,Zk下估计状态Xj,Xj+1,…,Xk的概率函数,并使之最大。假设所述的姿态运动系统的状态转移和观测噪声都符合高斯白噪声分布,则根据马尔可夫过程的概率密度函数的定义,可以根据则全概率将系统的概率密度函数定义为
P(Xj:k|Zj:k)∝
(24)
通过取对数,式(11)求解最大后验概率问题转化成求下列解式代价函数最小问题:
(25)
当新的状态与因子引入之后,对新的因子图进行全局优化不需要全部重新计算,而是利用之前优化过程中的信息,即因子图的增量特性,从而可以大大减少因子图的优化问题中的计算量。在考虑磁强计星敏感器、陀螺组合导航情况下,姿态确定的问题可以描述成求解下列最小值为问题。
(26)
可以看出,如果有新的节点的引入,目标函数对应增加了新的多项式和,由此传感器的增删变得简单,但是计算量由此增加。由于传感器制造工艺、使用环境、本身观测方式的不同,不同传感器获取的姿态信息质量不一,因此本文提出的基于改进因子图模型的多源信息融合技术,提出了一种观测蒸馏法,通过计算观测残差,设定阈值,将观测数据集进行提炼,信息提炼成两部分,一部分为高质量观测信息,另一部分为低质量的观测信息,为了降低低质量观测信息的影响,将低质量观测信息的均值、协方差矩阵和权值进行自适应调整,实现对观测不确定模型调整修正,将修正的观测量作为节点增量更新因子图,从而减少整个系统的计算量,提高整个系统的精度。其具体流程如图5所示。

图5 采用观测蒸馏的改进因子图模型流程图
具体方法如下:计算窗口M内的观测残差表示为
R=[r1,r2,…,rM]ri=|Zi-hn(Xi)|
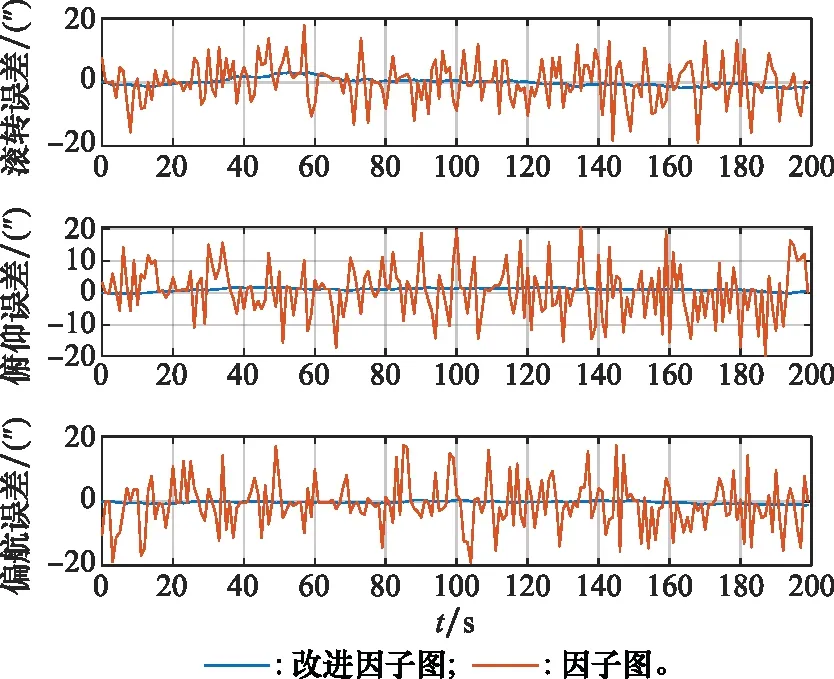
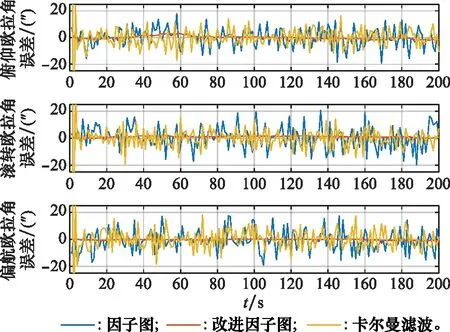
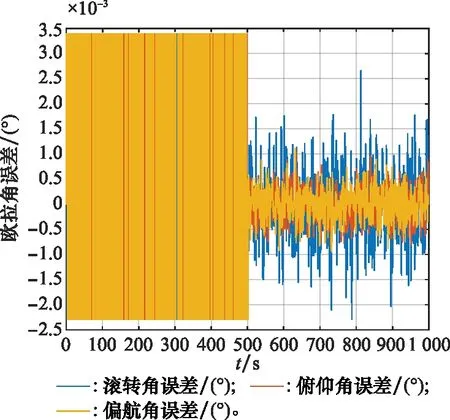
假设观测不确定模型满足均值为μ,均方差为σ的正态分布,将观测残差偏移值为G(ri,μ,Λ)=(ri-μ)/σ,其中Λ为观测残差的协方差矩阵。计算新的观测信息残差系列,给定阈值Td,将满足观测残差阈值的部分表示为:Ro={r|r∈R,G(r,μ,Λ) 为了定量的描述低质量观测的可靠性,首先对Rn进行cholesky分解得到新的目标变量Y,目标变量Y表示为 Y=[L-1r1,L-1r2,…,L-1rm] (27) 式中:μy和Λy为转置的观测残差Y的均值与协方差矩阵。 为了分析低质量观测值的特性,对其均值和协方差进行检验,构建值: F(d,n-d)。 对其均值和协方差真进检验卡方检验和F检验。如果均值和协方差与高质量模型一致,那么自适应调整不确定模型的均值协方差以及权值: (28) 如果低质量观测信息的均值和协方差不一致,与则调整该观测源的权值;如果观测残差的均值超过阈值则将权值置零,调整方式如下所示: (29) 改进的因子图模型可以描述为 (30) 通过求解得到状态的误差四元数,通过误差四元数计算姿态四元数的方式如下: (31) 在进行多传感器组合测姿时,将基于不同模型需要进行的步骤进行对比[30],如表1所示。 表1 不同方式重新进行组合测姿方案步骤对比 基于因子图模型的地磁姿态确定可具有较强的扩展性,可以合理充分地利用其他测量信息,在面对复杂情况具有较好的包容性,可以实现即插即用,但是由于保存了一顿时间内所有状态和观测量,使得相对计算量较大,随着计算力的不断提高及增量优化算法的改进,计算量不是限制问题。基于因子图模型的地磁姿态确定可为应对未来复杂的空间环境提供较好的模型平台。 GTSAM 是一个基于因子图模型的开源的C++优化库,用因子图和贝叶斯网络算最大化后验概率,使用增量平滑算法。本实验针对三轴稳定状态下的航天器进行姿态确定,传感器采用磁强计、星敏感器、陀螺进行递推估计和固定滞后平滑过程,观测的蒸馏通过Matlab算法进行实现。 针对500 km低轨对地三轴稳定卫星,其基本轨道和姿态参数如下。 (1)J2000惯性坐标系下设置该卫星的轨道六根数初始值如表2所示。 表2 卫星轨道6根数初始值 (2)敏感器的参数配置及模型噪声设置如下:磁强计的测量精度为10 nT;星敏感器的测量精度为10″;陀螺的漂移为1°/h;转动惯性为[2.683,2.326,1.897]kg2/m3;采样间隔为1 s; (3)改进因子图的参数设置:Td=10-5,Tr=10-2。 首先利用扩展卡尔曼滤波(extended Kalman filter, EKF)对基于星敏感器的航天器姿态确定进行仿真,星敏感器的精度和其他参数设置同第3.1节所示,姿态确定后的欧拉角误差如图6所示。 图6 基于EKF的星敏感器航天器姿态确定欧拉角误差 利用欧拉角误差的标准差来衡量精度的大小,其计算方式为 仿真结果表明,当存在初始误差时,滤波器经过10 s左右收敛到稳定状态。稳定后基于卡尔曼滤波模型三轴欧拉角误差为[6.126 5,6.393 0,6.760 9]″,整体精度为:11.140 7″。在利用因子图框架并采用星敏感器进行航天器姿态确定的情况下,可以看出基于因子图模型的航天器姿态确定方法不需要前期动态稳定的过程,因此姿态确定的整体精度会更高。 为避免奇异性,本文采用误差四元描述姿态运动变化,利用因子图对误差四元数进行递推估计,利用误差四元数使用四元数乘法计算得到姿态四元数。为验证本文所提出的方法在复杂条件下可以实现即插即用,且具有较好的动态稳定性,考虑复杂条件包括: (1)敏感器出现阶段性失效; (2)敏感器测量噪声非高斯分布。 进行以下实验。 实验 1星敏感器进行姿态确定,验证该方法的有效性。 采用本文所提出的方法的航天器姿态确定欧拉角误差结果,如图7所示。 图7 改进因子图前后的航天器姿态确定欧拉角误差 由仿真结果可知,稳定时基于因子图的航天器三轴欧拉角误差为[6.504 2,7.994 8,7.451 2]″,整体精度为12.717 8″;基于改进后因子图的三轴欧拉角误差为[1.187 9, 0.516 7,0.377 0]″,整体精度为1.349 2″。 将采用因子图进行组合姿态确定与采用EKF进行姿态确定对比,卡尔曼滤波的初始设置如表3所示。 表3 卡尔曼滤波仿真参数初始设置 将基于因子图、改进因子图与EKF的航天器姿态确定误差进行对比,如图8所示。 图8 3种姿态确定方案对比 图9 3种姿态确定方案整体姿态欧拉角误差 3种姿态确定方案对比如表4所示。 表4 3种姿态确定方案对比 通过实验仿真对比可知,改进后因子图模型的姿态估计算法具有较好的精度,该算法可以通过观测蒸馏法、自适应确定权重,来显著降低低质量观测对姿态的影响,并通过平滑姿态曲线,提高姿态确定的精度。同时,由于该方法具备一定的野值故障排除作用,并通过滑动窗口的滞后优化,缓解了状态量过多时计算量大的问题。 实验 2整体仿真时间为1 000 s,第一阶段(0~500 s)采用磁强计定姿;第二阶段(500~1 000 s)采用磁强计、星敏、太敏和陀螺组合定姿。验证该方法可以实现即插即用,并在动态切换的时候,具有较好的动态稳定性。 图10 有传感器缺失的姿态误差曲线 图11 有传感器缺失的姿态误差曲线局部图 在该实验中,第一阶段采用磁强计进行姿态确定,精度为0.2°,第二阶段将星敏感器通过添加节点的方式引入组合定姿中去,实现多传感器的融合,精度可达0.002°。实验结果表明,该方法可以从第一阶段流畅地切换到第二阶段,具有较好的动态稳定性,可以实现传感器的即插即用。 本文提出的基于因子图模型的航天器姿态确定方法是一种扩展性较强的组合测姿方法,可以合理而充分地利用其他姿态测量信息,避免了复杂的系统重构过程,减少了系统的设计复杂度,有利于新算法的拓展和多传感器的使用。实验结果表明,基于改进因子图模型的姿态确定具有较好的动态稳定性,同时,本文提出的方法针对复杂情况下的航天器姿态确定,可以对基于因子图的姿态确定进行平滑,精度为1.349 2″。另外,该方法具有较高的扩展性,以及动态稳定性,可以应用在复杂条件下的航天器多传感器组合定姿任务中。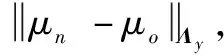
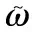
3 仿真验证
3.1 仿真条件

3.2 仿真结果与分析





4 结 论

