基于SCB方差的GNSS欺骗式干扰检测算法

王文益, 龚 婧, 王金铭

(1.中国民航大学电子信息与自动化学院, 天津 300300;2.中国民用航空局空中交通管理局技术中心, 北京 100015)

0 引 言

随着民用基础设备对全球卫星导航系统(global navigation satellite system,GNSS)的依赖日益加深,加上潜在的经济利益和恶意干扰,间接加速了GNSS欺骗设备的出现[1]。通常,这类欺骗设备具有一定的目的性:向目标接收机提供错误的导航位置信息。此外,欺骗设备可以操纵目标接收机以输出欺骗者预期得到的信息[2]。因此,检测GNSS欺骗设备的存在已经成为一个亟待解决的国际问题。

欺骗检测算法的有效性取决于欺骗设备的复杂程度,根据欺骗设备的复杂程度可以将欺骗攻击分为3大类:简单欺骗攻击,中级欺骗攻击和复杂欺骗攻击。其中中级欺骗攻击又可称为携带攻击,欺骗设备与GNSS接收机直接连接,获取真实信号的当前参数[1]。欺骗设备发送的信号与导航卫星发送的真实信号精确同步,并且能在接收机跟踪环路不失锁的情况下成功欺骗目标接收机[3]。

目前现有的中级欺骗检测技术可以分为3类:天线技术、测量域技术和基带信号处理技术。天线技术通过提取并判断接收信号的空域信息来检测和抑制欺骗[4-5]。这类技术虽然有效但是需要的设备成本大,且设计要求高。测量域技术检测测量合理性和冗余信息的一致性,用于检测GNSS接收机的欺骗式干扰[6]或检测GNSS/惯性导航系统(inertial navigation system, INS)集成中的多重故障[7],但当检测值的变化不显著时,此类技术并不适用。基带信号处理技术是检测在基带信号处理过程中容易获取的差异变化,该技术需要修改或重新设计接收机的信号处理算法以检测中级欺骗[8],该技术为欺骗检测提供了一个新的方向,也是当前比较热门的检测技术。

基带信号处理技术可以分为3类:信号功率检测技术、导航信息检测技术和信号质量监视(signal quality monitor,SQM)技术。信号功率检测技术适用于欺骗信号功率高于真实信号功率且有较大差异的情况[8-9],对于中级欺骗而言,欺骗信号和真实信号的功率近似,因此该方法的应用受到限制。导航信息检测技术用于检测信号码率和相位率,对于真实信号而言,卫星与接收机之间相对运动产生的多普勒频率和码速率具有一致性[10],而中级欺骗在一定程度上也可以保持这种一致性,因此此方法基本无效。

近年来,SQM技术引起了GNSS领域专家学者的广泛关注。与上述提到的其他检测技术相比,SQM算法通过对GNSS接收机跟踪环路中早码、即时码和晚码相关器的输出值进行计算,有利于识别相关函数的形变[11]。SQM技术的简单性和有效性使其在多径检测和欺骗检测中备受青睐。最初Phelts介绍了两种基础的SQM技术:Delta算法和Ratio算法[12]。Delta算法主要用于检测相关峰的不对称性,而Ratio算法主要用于检测相关峰的异常尖锐和平坦。这两种指标最初应用于检测多径干扰,而最近的研究证明，监视欺骗信号与真实信号重叠过程中SQM指标的变化,对欺骗检测也是有效的[13]。Double-Delta算法可以看作是Delta算法的优化,是基于跟踪和监视两对早晚码相关器之间的差异而进行的进一步开发并应用于检测GNSS信号失真和多径的方法[14-16]。早晚期(early-late phase，ELP)算法利用早码和晚码相关器输出的相位差来检测多径干扰,也被证明可以有效地对欺骗信号进行检测[17-18]。为了进一步提高欺骗检测的可靠性,Pirsiavash等人还提出了通过在多普勒频率域中引入检测度量来开发二维SQM的方法[19]。此外,将SQM技术与功率畸变监测器相结合的功率失真(power distortion，PD)检测器不仅可以检测欺骗攻击,还可以将其与多径和干扰区分开[20]。对称差异(symmetric difference, SD)度量也可用于检测包含欺骗信号的异常GNSS信号引起的相关峰中的失真。而极大似然PD(maximum likelihood PD, DM-ML)检测器利用来自额外抽头的数据执行最大似然估计对SD度量进行改造,该方法显著的提高了SD技术的性能,但是要以增加计算的复杂性作为代价[21]。最近,提出了通过观察阈值变化值来证明检测欺骗信号的可行性,但这种技术更多的依赖于后相关值[22]。

本文选择能够充分利用中级欺骗动态特性的过零点S曲线偏差(S curve bias,SCB)技术进行研究[23-24]。考虑到由于信道传输失真和功率放大器非线性效应的影响而导致在不存在欺骗时SCB值会存在一定程度的波动,并且在欺骗攻击存在的初期,由于真实信号和欺骗信号的重叠也会导致SCB值的显著波动,类似于系统噪声[25]。综合上述分析,在整个检测过程中都会存在SCB值波动较大的现象,所以直接使用SCB值作为检测指标将间接导致检测率也受到影响。本文结合Sun等人提出的基于移动方差的信号质量检测方法[25]提出了一种基于SCB方差的GNSS欺骗式干扰检测算法,利用方差特性可以更好地反应欺骗信号和真实信号在重叠过程中S曲线过零点产生的偏差波动情况,并可直接作为检测参量。

本文介绍了全球定位系统(global positioning system, GPS)信号和GPS欺骗信号模型,给出了基于SCB方差的欺骗式干扰检测算法的原理介绍,基于TEXBAT的第7条中级欺骗的实采信号进行检测的实验分析。

1 信号模型

以GNSS中使用最为广泛的卫星信号(C/A码)为例,中级欺骗过程如图1所示。图1(a)是欺骗信号在低功率情况下滞后于真实信号两个码片并以不同于真实信号的码速率进入跟踪环路的阶段。从图1(a)到图1(b),欺骗信号逐渐靠近真实信号,并且以高于真实信号的功率进行干扰,欺骗信号最终将与真实信号在码相位维度上对齐,在这种情况下,欺骗信号与真实信号在载波频率和码相位上完全同步。随后,欺骗信号保持高于真实信号的功率向右牵引,直到目标接收机的跟踪环路锁定在欺骗信号上,如图1(c)到图1(d)所示。最终,导致目标接收机计算出错误的导航位置信息。

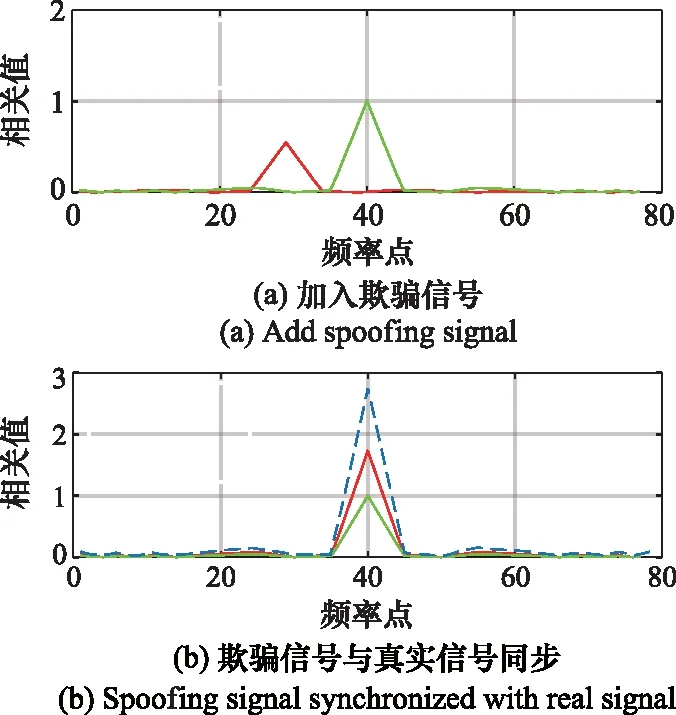
图1 中级欺骗攻击示意图

单天线接收的混合信号由真实卫星信号、欺骗信号及噪声组成。目标接收机接收到的t时刻中频信号可表示为

x(t)=xa(t)+xs(t)+n(t)

(1)

式中：xa(t)表示真实卫星信号;xa(t)表示欺骗信号;n(t)表示均值为0且方差为σ2的高斯白噪声。

真实卫星信号的中频信号可以表示为

(2)

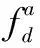
根据前文欺骗过程的分析,已知欺骗信号有与真实信号相同的结构,因此欺骗信号的模型为

(3)

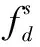
对于GPS卫星信号中L1载波频带的C/A码,本地码和接收到的混合卫星信号互相关函数可通过载波剥离和1 ms的相干积分得到,表示为

(4)

(5)

由欺骗特性可知欺骗信号随时间变化,即

(6)

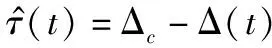
(7)

(8)

式中:xa, j和xs, j分别是第j颗卫星的真实信号和欺骗信号。

码跟踪环路采用非相干鉴相器,即所利用的相关值不依赖于载波相位误差,独立于载波环路。超前、即时与滞后支路的相关器输出表达式为

(9)

(10)

(11)

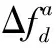
2 检测算法

2.1 SCB算法

目标接收机通过码跟踪环路中的码鉴别器曲线(即S曲线)过零点获得对应的码相位值[23]。在无干扰和噪声的情况下,S曲线过零点对应的码相位值为0,实际上由于信道传输失真和功率放大器的非线性效应影响,码相位值会在零值附近波动。当存在欺骗攻击时,码相位值将会偏离零值产生SCB,如图2所示。SCB值用来衡量码跟踪误差,即可作为检测欺骗攻击的标准。

图2 S曲线示意图

在码鉴别器算法的选择上,相干型与非相干型计算的S曲线相差不大,但实际硬件接收机中多采用非相干型[26]。因为相干型鉴别器算法与载波相位跟踪误差有关,当环路未稳定跟踪时,接收信号的能量将分布在同相和正交支路上,且幅值型计算量大于功率型,本文中考虑非相干功率鉴别器,其S曲线可用表示为

Scurve(ε(t),d)=|E[ε(t)]|2-|L[ε(t)]|2

(12)

其中，ε(t)为随时间变化的SCB函数满足:

ε(t)=arg{Scurve(ε(t),d)=0}

(13)

2.2 SCB方差算法

然而,中级欺骗信号所引起的类似于系统噪声的波动会间接影响检测性能。文献[23]提出的SCB算法中利用均值在一定程度上可以平滑类似于系统噪声的波动,但由于欺骗过程中SCB值会有正负的变化,求其均值的同时也会降低SCB的幅度,并且利用SCB均值进行检测仍然需要同时设置上下两个检测门限即Thu和Thl,就不可避免地在欺骗信号与真实信号同步的过程中使SCB值浮动在正常范围内的时间变相被延长,在一定程度上还会恶化欺骗检测性能。

而方差是用来度量变量与其数学期望(即变量的均值)之间偏离程度的,所以可以利用方差更好地反映某一时间段内SCB曲线的波动情况,提高SCB检测性能。且在GPS接收机中经过滤波,以及对接收到的信号和本地信号进行相关运算后,会降低噪声对卫星信号的影响,所以SCB方差值更大程度上是受欺骗攻击的影响而发生变化。SCB方差算法原理图如图3所示。

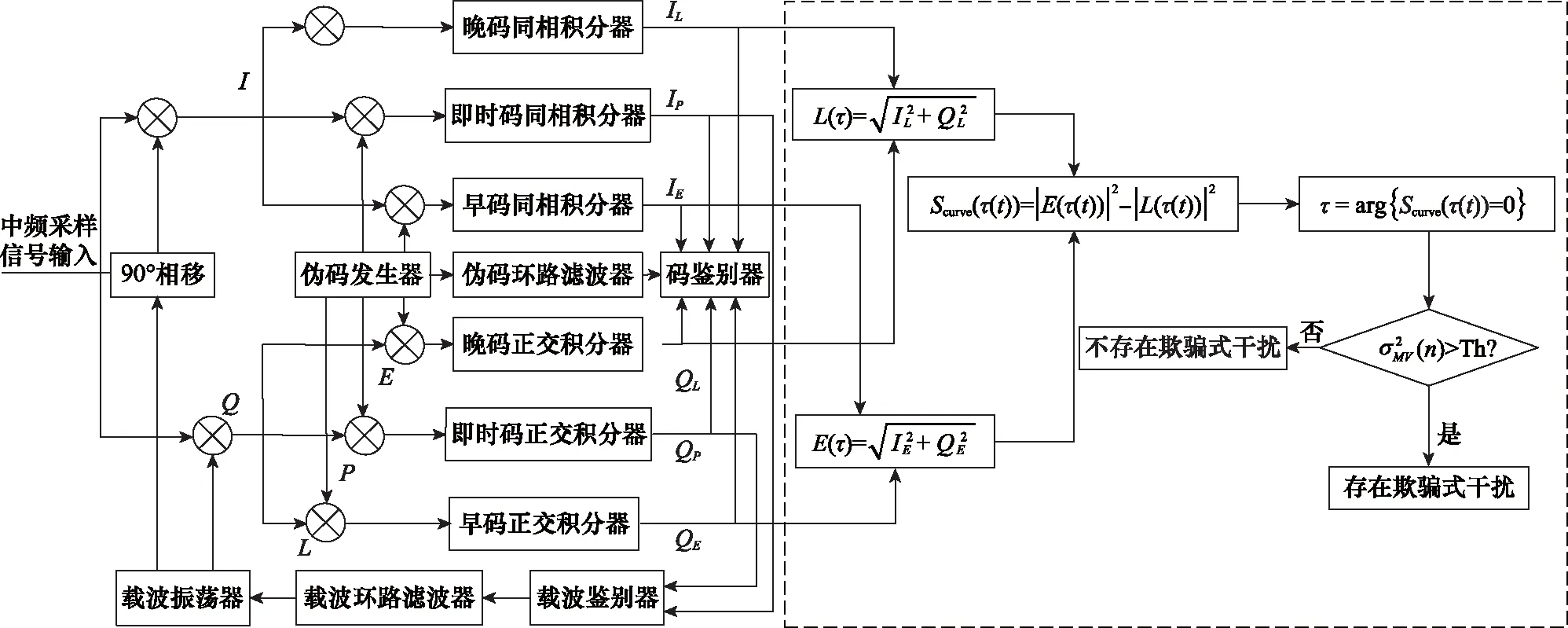
图3 SCB方差算法原理图

如图4所示,通过计算移动窗口中SCB数据集的方差值,并将移动窗口随时间向前移动计算新的方差值,重复该过程,将计算得到的每个移动窗口的SCB方差值组成新的数据集,即获得SCB的方差函数。

图4 方差示意图

SCB方差函数的表达式如下:

(14)

图5所示为通过该算法进行欺骗式干扰检测的过程。

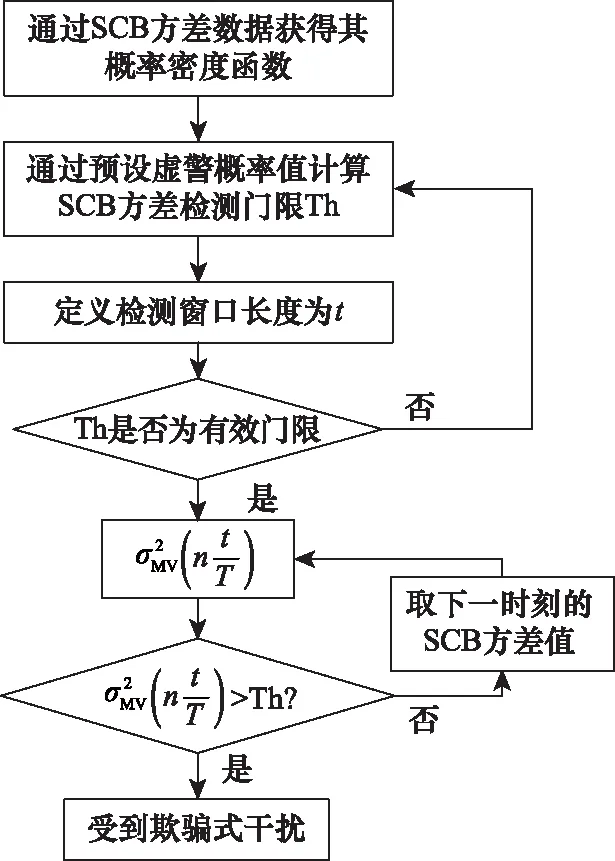
图5 SCB方差算法检测流程图

2.3 检测门限及概率分析

检测到欺骗攻击真实性的验证分析可以被视为二元信号检测问题,即将欺骗攻击检测分为两个判决假设情况,假设H0为不存在欺骗攻击,H1为存在欺骗攻击。定义二元信号检测函数为

(15)

在二元信号的情况下,共有4种可能的判决结果,本文只考虑其中的两种判决结果来分析检测性能,即虚警概率和检测概率。

虚警概率Pfa是在没有受到欺骗攻击的情况下错误判断欺骗攻击存在的假设概率,检测概率Pd则是在存在欺骗攻击的情况下正确判断欺骗攻击存在的假设概率。虚警概率也可视为关于检测门限的函数,因此首先要获得在不存在欺骗攻击卫星导航信号数据情况下SCB和SCB方差的概率密度函数。

以码跟踪环路即时码相关器输出值P为例,近似服从莱斯分布[27],其概率密度函数为

(16)

(17)

而即时码相关器输出值的平方服从自由度为1的卡方分布,由卡方分布的性质可知,卡方分布只具有可加性,所以式(12)即S曲线的概率密度无法求得,进而SCB的具体分布也无法准确定。

因此,假设SCB的虚警概率为Pfa1,是SCB值大于上检测门限Thu且小于下检测门限Thl的概率之和[25],计算公式为

(18)

式中:p(ε(t);H0)表示不存在欺骗干扰时SCB的概率密度函数。

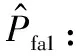
(19)

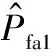
为了推导检测概率Pd1,需知存在欺骗攻击的情况下SCB的分布。但是,分布取决于目标接收机的跟踪环路配置和特定的欺骗攻击模式。由于中级欺骗攻击的欺骗过程具有时变特性,目标接收机在欺骗信号功率和码相位未知的情况下,使得存在欺骗攻击的情况下SCB的分布非常复杂,因此通过推导概率密度函数的解析表达式来计算检测概率Pd1不切实际。

(20)

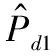
同理,假设SCB方差的虚警概率为Pfa2,是关于SCB方差给定门限值Th的函数,即

(21)

(22)

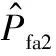
(23)

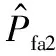
3 实验分析

根据前面的理论分析,将本文所提算法嵌入到传统GPS软件接收机中。本文将实验分析建立在美国德克萨斯州大学奥斯汀分校无线电导航实验室于2012年公开的欺骗攻击影响的GPS卫星信号公共数据库TEXBAT的基础上[29]。根据中级欺骗攻击的特性,选取第7条数据即频率锁定的诱导式欺骗干扰进行检测实验和性能评估。

3.1 原始SCB值检测

本组实验使用第7条数据进行实验分析,即对中级欺骗攻击模式的检测分析。欺骗信号数据的采样率为25 MHz,C/A码码速率为1.023 MHz,欺骗信号功率高于真实信号功率1.3 dB,选取欺骗信号数据总长度为400 s,欺骗攻击开始时间为第110 s,初期欺骗攻击码相位滞后于真实信号两个码片,随着时间的变化,欺骗信号逐渐与真实信号重叠。当欺骗信号与真实信号在码相位维度上对齐时,目标接收机由欺骗信号控制。在欺骗信号与真实信号重叠的过程中S曲线发生畸变,进而导致SCB值偏离零点。

本文的原始SCB值区别于文献[23]提出的SCB值,是指没有经过滤波和求导处理的GPS接收机直接得出的SCB值。以捕获跟踪到的23号卫星为例,图6表示PRN23的SCB值检测结果,从110 s开始，SCB值逐渐偏离零点且为负值,这表明欺骗信号滞后于真实信号的码相位。当SCB值达到最大负值后逐渐增加至0,此时欺骗信号与真实信号同步,并以高于真实信号的功率优势控制接收机码跟踪环路。随后,欺骗信号逐渐脱离真实信号。

图6 SCB算法检测结果

图7是在欺骗攻击的整个持续时间内,采用恒虚警率处理的SCB的检测概率随时间变化的曲线,即每10 s计算一次超过检测门限的SCB值和SCB总样本个数的比例。根据式(18)可得,在预先设定虚警概率为10%时的上检测门限Thu=0.040 716,下检测门限Thl=-0.042 083。由图6中可以看到SCB曲线与中级欺骗攻击过程基本吻合,在第110 s加入欺骗攻击后,检测率基本稳定在60%左右,并在欺骗攻击控制接收机之后的检测率高达90%,在210 s左右检测率能达到100%。

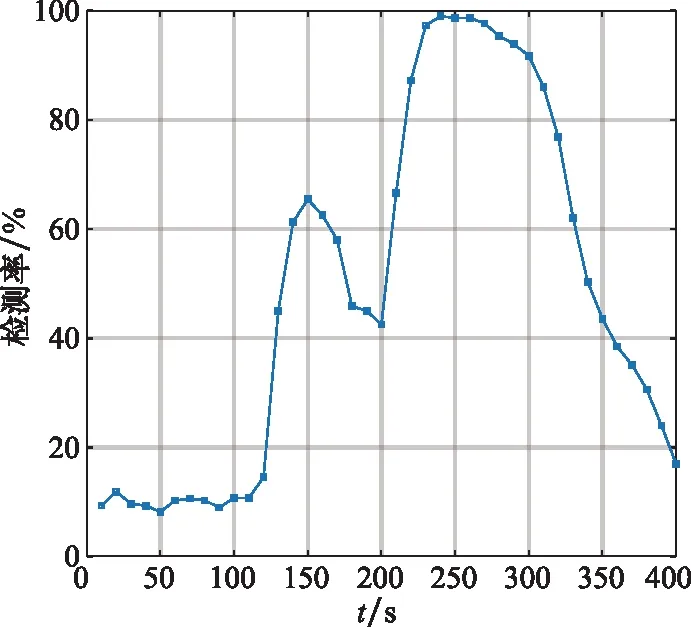
图7 SCB算法检测率随时间的变化趋势

为了进一步对检测性能进行分析,图8说明了在任意假设的虚警概率下对欺骗攻击的检测能力,也称为接收者工作特征(receiver operating characteristic, ROC)曲线。ROC曲线上的点越靠近左上角,检测的准确性就越高,在SCB算法检测中,当虚警概率约为17%时,整个欺骗过程检测率能达到68.7%左右。

图8 SCB算法ROC曲线

3.2 SCB方差检测

SCB方差算法检测的实验环境和原始SCB算法一致。如图9所示,在加入欺骗信号的110 s后随着欺骗信号以略高于真实信号的功率靠近真实信号,码相位逐渐和真实信号码相位对齐,S曲线发生畸变,SCB值偏离零点,导致SCB方差值逐渐增加。SCB方差值达到最大值的时刻对应SCB值在负方向上的最大值;后又回落至零值附近,即欺骗信号与真实信号同步;随着欺骗信号逐渐脱离真实信号,SCB方差值再次增加,最终回落至零值附近。SCB方差值表明当存在欺骗信号时,导致码相位偏离零点的离差情况。

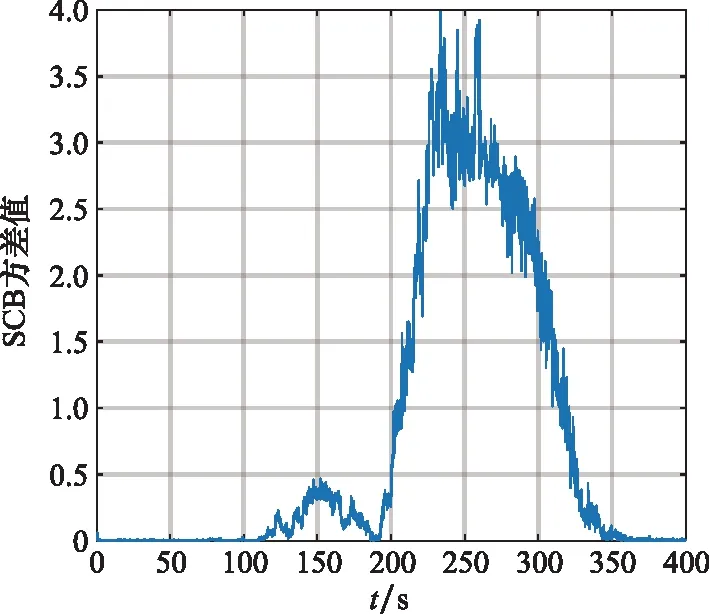
图9 SCB方差算法检测结果

根据式(20)可得,在预先设定的虚警概率为10%的情况下SCB方差值检测门限Th=0.0043 212。图10所示是在欺骗攻击的整个持续时间内SCB方差算法的检测结果,其中方差算法的移动窗口分别选取ω=100 ms、ω=200 ms、ω=400 ms。当ω=200 ms时,SCB方差算法能够准确地在110 s检测到欺骗并且检测率基本保持在90%以上,随移动窗口大小的增加,在目标接收机被欺骗信号控制的期间检测效果也有所改善。当ω=400 ms时,110 s加入欺骗时的检测率可达到100%。

图10 SCB方差算法检测率随时间的变化趋势

进一步分析SCB方差算法的检测能力,如图11所示,SCB方差算法在一定程度上能提高原始SCB算法的检测准确性,当SCB方差算法的移动窗口为400 ms且虚警概率约为10%时,整个欺骗过程的检测率能达到96%以上。如图12所示,SCB方差算法的ROC曲线随着移动窗口的增加而改善。当移动窗口长度为1 s、虚警概率为10%时，检测率几乎能达到100%。

图11 SCB方差算法在不同移动窗口下的ROC曲线

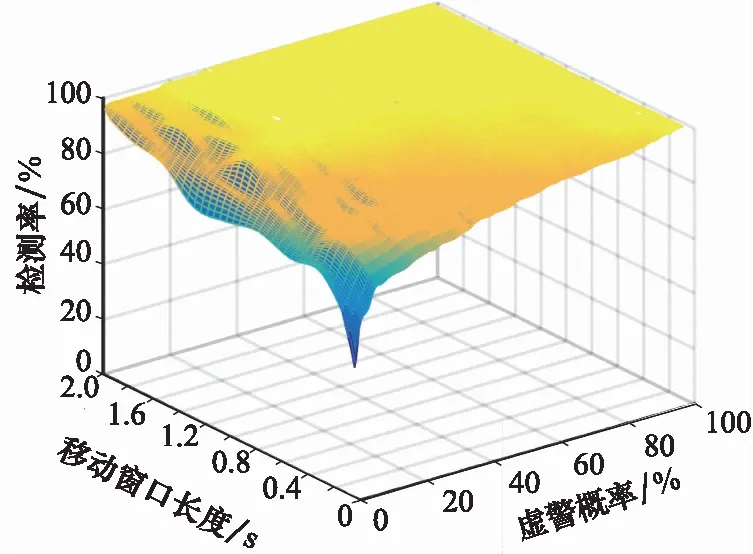
图12 SCB方差算法检测率在窗口长度以200 ms为单位增长的情况下随虚警概率的变化趋势

3.3 SCB方差与其他算法的对比

在同一载波频率锁定的诱导式欺骗干扰环境下,将原始SCB算法、Ratio算法[11]和复合SQM算法[30]及本文所提方差算法分别应用于以上3种算法的检测率作比较,结果如图13所示。可以看出,在前110 s不存在欺骗攻击的期间,各算法的检测率均在10%左右,与所选择的虚警概率为10%一致。Ratio算法在110 s至200 s内的检测率均不高,直到340 s检测率才能达到85%以上;复合SQM算法将Ratio算法和ELP算法进行幅度组合,能够达到比Ratio算法更早检测到欺骗信号的效果,在230 s时检测率可以达到80%以上;而原始SCB算法在110 s至150 s内检测率达到65%左右,在欺骗信号加入的初期就能够检测到,但是检测率依旧较低。方差算法能够在一定程度上提高3种算法的检测率,当移动窗口ω=400 ms时,SCB方差算法能够准确地在110 s检测到欺骗并且检测率基本保持在100%,检测性能优于和Ratio方差算法和复合SQM方差。

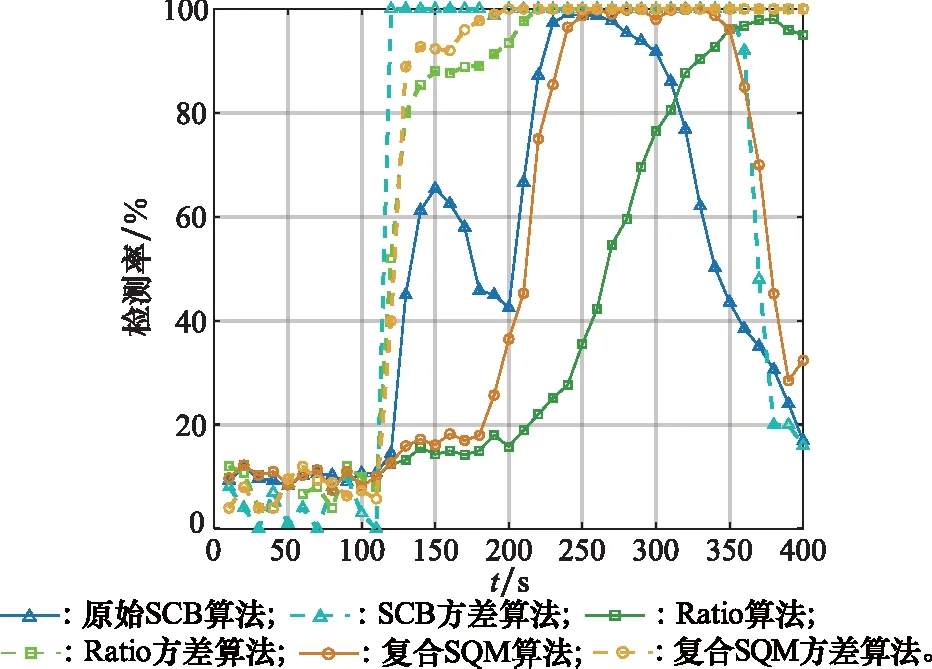
图13 3种算法及对应方差算法检测率比较

如图14所示，将3种算法以及方差算法分别应用于以上3种算法的检测率随虚警概率变化的趋势进行了比较,且方差算法的移动窗口ω=400 ms。显然,SCB算法体现了其检测性能的优越性,并且SCB方差算法的检测准确性比原始SCB算法有所提高。

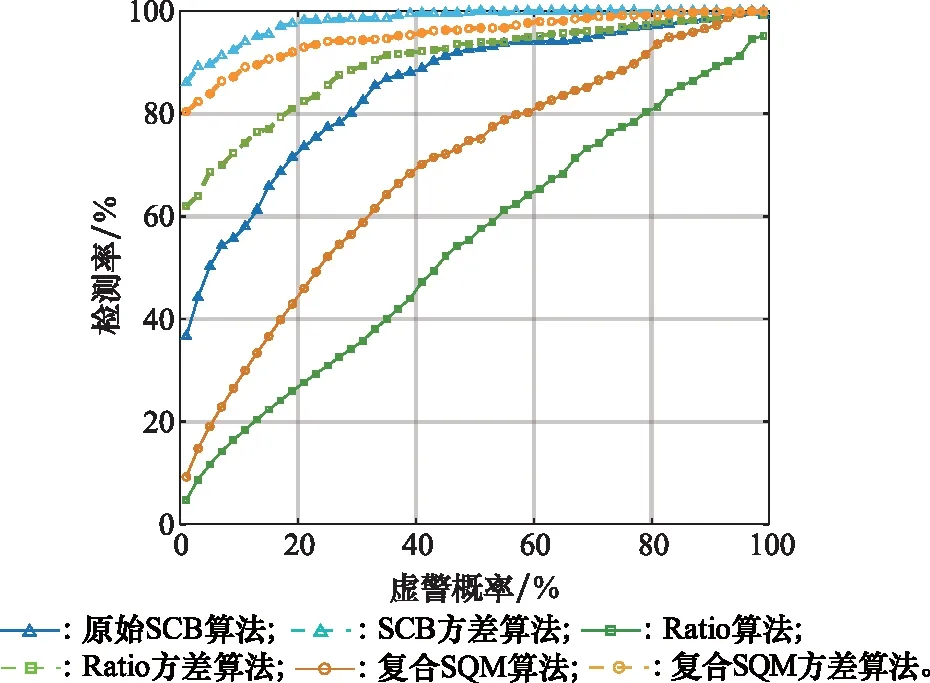
图14 3种算法及对应方差算法ROC曲线比较

4 结 论

本文利用诱导式欺骗干扰的动态特性并结合方差特性提出了一种能反映欺骗过程中S曲线过零点码相位偏差波动情况的欺骗式干扰检测算法;通过判断SCB方差值是否超过给定的检测门限来判断是否受到中级欺骗的攻击;结合德州大学实采的中级欺骗实采数据进行实验分析,以验证算法的有效性。通过多种算法的比较可以看出,诱导式欺骗干扰以其可控可变的功率优势在一定程度上避开了Ratio算法检测复杂的问题,复合SQM算法同时利用了同相和正交通道的信息,可以比Ratio算法在更早的时间内检测到欺骗,但对于隐蔽性更强的功率和码相位均随时间变化的频率锁定诱导式欺骗攻击,SCB方差算法则体现出了更好的检测性能。