基于VISSIM仿真的干线绿波交通协调控制设计

詹 斌， 田园园， 朱家明

(1.武汉理工大学 交通学院,湖北 武汉 430063；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

0 引 言

随着经济水平的提升,我国近年来私人汽车保有量逐年增加。数据统计显示，2018年我国私人汽车拥有量为20 574.93万辆,较2017年的18 515.11万辆增长了11.13%[1]。私家车出行已成为市民出行的主要交通方式，但伴随而来的就是城市交通常态化拥堵。为了缓解城市交通拥堵这一难题,国内学者进行了诸多研究。

石佳等[2]以紧密联系的交叉口所构成的OD路径为切入点,建立了智慧子区划分算法,在智慧子区内部实行“线轴”结合控制,通过仿真验证发现实施新型控制方案后能有效提高交通子区通行量;曲大义等[3]运用交通波理论阐释了干线车流排队现象,揭示了大流量线控系统绿波交通产生的内在机制,结果表明城市干线绿波交通可以提高干线运行效率,但却增加了其交叉支线的行程延误;施俊庆等[4]利用微观仿真软件VISSIM对城市主干道双向绿波交通实施效果进行了评价,表明在特定流量下,实行干线绿波交通能有效减少主干道延误,且车辆速度和相位差均对绿波交通实施效果有显著影响。田家斌等[5]提出适用于不同层次、不同特点的交叉口相位相序结构建立相位差协调策略算法利用相序的调整设计交叉口的配时优化方案来实现干线道路双向绿波协调控制。夏井新等[6]针对现有干线交通信号绿波控制方法采用平行等宽的绿波带宽无法考虑相邻交叉口间交通流运行速度波动性的缺陷，引入了基于路段速度波动区间的不等绿波带宽，提出了干线交通双向绿波优化控制方法。

上述学者的研究中均提出城市干线绿波交通能够有效改善城市交通状况,提高道路运行效率并减少空气污染。在此基础上,本文建立了城市干线绿波交通模型,并以山东省青岛市瑞昌路某一日晚高峰为例进行实例验证,将模型得出的配时方案加载到VISSIM仿真环境,评估模型的有效性。

1 干线绿波交通模型建立

1.1 单点交叉口高峰小时交通量

在调查中,取5 min连续时段内的统计交通量,此连续5 min所计交通量最大的那个时段,就是高峰小时内的高峰时段,把高峰时段的交通量扩大为1 h的交通量即为高峰小时交通量。

因此对于已选定高峰时段的交通量,需按该高峰时段内交叉口各进口道不同流向分别确定,其计算公式如下:

qdmn=12×Q5mn

(1)

式中:qdmn为配时时段中由进口道m流向出口道n的交通量，pcu/h,即为扩大的高峰小时交通量;Q5mn为配时时段中由进口道m流向出口道n的高峰小时中最高5 min的流量，pcu/5min。那么,在配时时段中,由进口道m流向出口道n的高峰小时交通量为:

Qdmn=qdmn×PHF

(2)

式中:PHF为高峰小时系数,指高峰小时交通量与高峰小时内某一时段的交通量扩大为高峰小时交通量之比,一般取0.85。

1.2 单点交叉口信号配时计算

根据每一交叉口的平面布局及计算交通量,按单点定时控制的配时方法,确定每一交叉口的周期时长,周期时长一般取值为40～180 s。单点交叉口信号配时计算步骤如下所示:

步骤一:计算信号总损失时间。按下式计算:

L=nl+AR

(3)

式中:L为总损失时间，s;n为信号相位数;l为相位的损失时间,取3 s;AR为一周期中的全红时间。

步骤二:计算车道饱和流量。饱和流量的定义是:在一次连续的绿灯信号时间内,进口道上一列连续车队能通过进口道停车线的最大流量,单位是pcu/h。饱和流量随交叉口几何因素、渠化方式、信号配时及各流量交通冲突等情况而异,比较复杂。饱和流量用实测平均基本饱和流量乘以各影响因素校正系数的方法估算。即进口道车道的估算饱和流量为:

Sf=Sbi×f(Fi)

(4)

式中:Sbi为第i条进口车道基本饱和流量，pcu/h;f(Fi)为各类进口车道的校正系数。

其中各进口车道的基本饱和流量见表1。

表1 各类进口车道的基本饱和流量

步骤三:计算流量比总和。按下式计算：

(5)

式中:Y为组成周期的全部信号相位的各个最大流量比y值之和;j为一个周期内的相位数;yj为第j相的流量比;qd为设计交通量，pcu/h;Sd为设计饱和流量，pcu/h。

步骤四:计算信号周期时长。信号周期时长需选用最佳周期时长,利用韦伯斯特(Webster)方法进行计算:

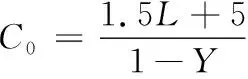
(6)

式中:C0为最佳周期时长,s;L为总损失时间,由式(3)可计算得到,即L为6 s;Y为交叉口流量比,由式(5)可计算得到。

实际上,由韦伯斯特方法计算得到的周期长度经过现场实验调查后发现,通常都比用别的公式算出的短一些,但仍比实际需要使用的周期要长。因此从实际情况出发, 为保证延误最小,周期可在0.75C0～1.5C0范围内变动。当交通量过小,容易造成信号周期设置过短,不利于行车安全。因此,需要人为规定周期取值下限,参考西方国家,一般为25 s。而当交通量过大,易造成周期过程过长,则车辆延误时间骤然极速增长,反而会造成交通拥堵。

步骤五:计算各相位有效绿灯时间。按下式计算:

(7)

式中:gej为各相位有效绿灯时间;Ge为交叉口总有效绿灯时间,即周期时长减去总损失时间;yj为各相位流量比;Y为交叉口总流量比。

步骤六:计算各相位显示绿灯时间。按下式计算

Gj=gej-lj

(8)

式中:lj为第j相位的损失时间。

1.3 干线交通信号协调控制计算

由上述单点交叉口信号配时方案可计算出每一交叉口所需周期时长。在实际的交通干线协调中,一般以所需周期时长最大的交叉口为关键交叉口,并以此周期时长为线控系统的备选周期时长。以各交叉口所需时长并根据主次道路的流量比,可计算各交叉口各相位的绿信比以及绿灯时间。假设干线上第m个交叉口为关键交叉口,那么:

gm=gme-Im+l

(9)

(10)

非关键交叉口上次要道路方向显示绿灯时间,是该交叉口对次要道路所必须保持的最小绿灯时间。显示绿灯时间以gn表示,有效绿灯时间以gne表示,则:

gn=gne-In-l

(11)

(12)

系统周期时长大于非关键交叉口所需周期时长时,非关键交叉口改用系统周期时长,其各相位绿灯时间均随之增长。非关键交叉口次要道路方向的绿灯时间只需保持其最小绿灯时间即可。为有利于线控系统协调双向时差,在非关键交叉口上保持其次要方向的最小绿灯时间,把因取系统周期时长后多出的绿灯时间全部加给主干道方向,这样还可适当增宽线控系统的通过带宽。

通过上述算法可计算得到线控交叉口周期与绿信比,但具体相位差还需根据实际案例进行具体分析。

2 实例验证

2.1 现状调查

本次实验以山东省青岛市瑞昌路干线5个交叉口为例,如图1所示。

图1 瑞昌路干线交叉口分布图

该干线路网规整,条路清晰,且主干道瑞昌路道路渠化较好,适合进行整体信号优化设计。通过整体信号优化后,可以降低行车延误和停车次数,提高市区整体通行效率,改善拥堵现状。本实验交通调查方式采用人工计数法,记录5个交叉口进出口道渠化现状，详见表2,并记录进口道转向流量。进口道转向流量包括左转、直行、右转、总和;从16∶00至21∶00，每间隔5 min统计一次并记录,部分原始数据如图2所示。

表2 各交叉口渠化现状

图2 瑞昌路金华路原始数据记录图

2.2 数据预处理

根据该交叉口交通量实测数据的对比分析,并对实测交通量进行系数换算,得到各个进口道高峰小时交通量、各个交叉口直行车大车率及最高15分钟流率换算的高峰小时流率qdmn，见表3～表7。

表3 交叉口1瑞昌路-广昌路晚高峰小时各流向流量表

表4 交叉口2瑞昌路-金华路晚高峰小时各流向流量表

表5 交叉口3瑞昌路-杭州路晚高峰小时各流向流量表

表6 交叉口4瑞昌路-人民路晚高峰小时各流向流量表

表7 交叉口5瑞昌路-吉水路晚高峰小时各流向流量表

2.3 瑞昌路干线协调控制

根据各个交叉口交通现状调研情况,结合流量变化统计,对单点路口进行方案优化。针对绿时损失、配时失衡等问题，通过整合道路资源,对路口时空资源的再分配,对路口进行优化设计。

本实验中包括5个交叉口,各交叉口间距示意图如图3所示,通过上述干线绿波交通模型计算得出公共周期时长为133 s,系统带速暂定为v=30 km/h,接下来利用“时空数解法”以实际调研情况计算理想信号偏移量。

图3 瑞昌路干线交叉口间距图

步骤一:计算a列即理想位置。先计算理想信号相位间距,S=VC/2=4×133/2=266。因此,相距266 m信号的时差,正相当于交互式协调的时差;相距532 m的信号,正是同步式协调。以266±50作为最合适的S的变动范围,即216～316,填a列,a列数字是假设理想信号位置,显然偏移量越小,信号协调效果越好。结果见表7。

步骤二:计算b列。将实际信号位置与理想信号的偏移量,按顺序排列(从小到大),并计算偏移量之差,将此差最大值填入b列,并计算216～316各行b值。结果见表8。

表8 “时空数解法”确定信号时差

步骤三:确定最合适的理想信号位置。由表8可知,当a=276时,b=224为最大值。取b为最大值时,对应的a值,即可得1～4各信号到理想信号的最小偏移量,确定理想信号相位间距为276 m,即当VC/2=276时,可以得到最好的系统协调效率。从计算b列的过程可以看出交叉口3～5与理想信号间偏移量之差最大为224,则理想信号与交叉口3之间的偏移量为:

(a-b)/2=(276-224)/2=26

因此,各实际信号距理想信号的偏移量最大为26 m。

理想信号距交叉口3为26 m,则距交叉口1为4 m,依次类推,如图4所示。

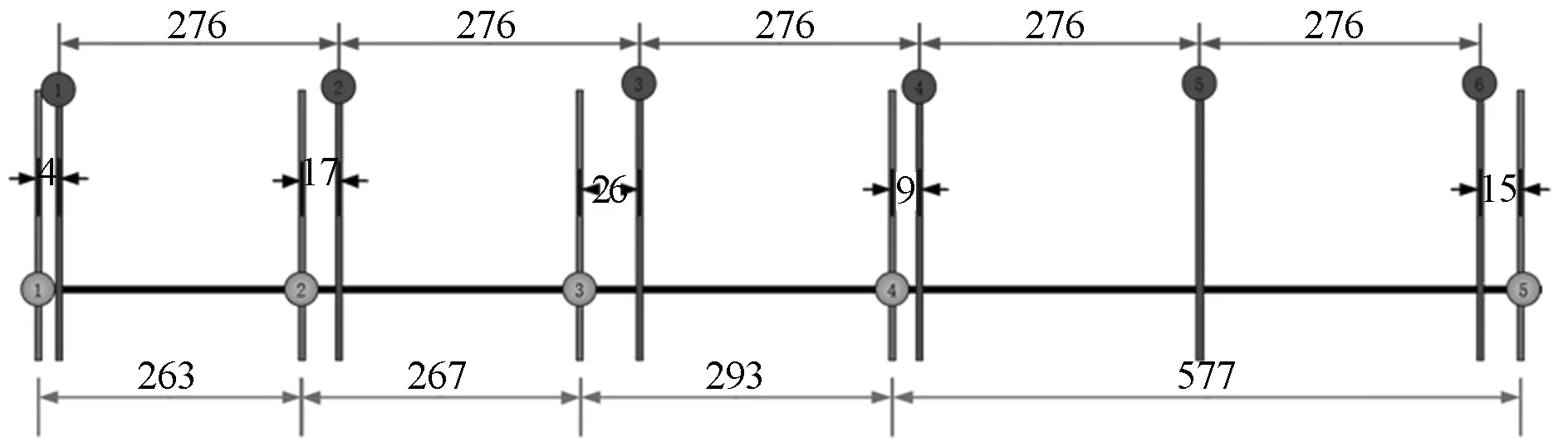
图4 理想信号与实际信号的相对位置(单位:m)

步骤四:计算相位差(绿时差)与绿波带宽度。在4中把理想信号依次列在最靠近实际信号下面,见表9。将1～5各信号在理想信号的左、右位置填入表9第三行。把各交叉口信号配时所得的主干道绿信比列入表9的第四行。因实际信号与理想信号位置不一致造成的绿时损失用其位置偏移量除以理想信号的间距表示,填入表9第五行。从各交叉口的计算绿信比减去其绿时损失即为交叉口的有效绿信比,填入表9第六行。

绿时差计算分为奇数和偶数λ。相应于奇数理想信号相位位置的实际交叉口绿时差为(100-0.5λ)%;相应于偶数理想信号相位的实际交叉口相位差为(50-0.5λ)%。

绿波带的带宽为左、右两端有效绿信比最小值的平均值。

计算结果见表9。

表9 计算绿时差及绿波带带宽

步骤五：利用人工调试方法得出最终的干线绿波控制方案,如图5所示。

图5 瑞昌路干线绿波控制方案

通过信号调优,对方案进行精细化配时,尽量使晚高期间峰实现绿波通行,避免相邻路口由于距离较近导致车辆溢出,但是随着车流量的变化,优化效果会降低,可通过人工巡检的方式进行效果的跟踪及保障。

3 VISSIM仿真验证

为了验证瑞昌路干线绿波交通控制方案的有效性,我们采用VISSIM软件进行仿真验证。VISSIM是一款道路仿真设计软件,可以在电脑上设计出建设道路的具体细节,特别是在城市交通道路分析方面。它可以提供微观的设计概念,分析所有城市交通模型,并且支持车道配置,交通组成及交通信号等设计。

本次仿真验证试验采用VISSIM4.3版本,车道宽度统一设置为3.5 m,车队组成为10%大巴车与90%小汽车,信号配时采用固定式信号机,以节点为评价对象,以行程时间、延误和排队长度为评价目标,仿真种子为10,仿真时间为3 600 s,每300 s统计一次数据并输出至文件夹。

首先在VISSIM仿真平台上建立瑞昌路干线模型,包括道路渠化方式,信号机参数,路径流向比例等,建立好的VISSIM仿真模型3D效果图如图6所示。

图6 瑞昌路干线VISSIM仿真效果图

然后分别输入瑞昌路干线绿波控制优化前后交通信号配时方案,如图7、图8所示。其中,图8中原控制方案为瑞昌路干线晚高峰交通量调查当天的汇总结果。输入方案后在VISSIM仿真平台中运行,得到行程时间、延误和排队长度的仿真数据。

图7 瑞昌路干线优化前控制方案

图8 瑞昌路干线绿波交通控制前后对比

最后,对行程时间、延误和排队长度仿真数据进行可视化处理,可知5个交叉口平均排队长度由原来的14 m降低到了11 m,降低了21.4%;平均延误由原来的239 s降低到了78 s,降低了67%,通过干线的行程时间由原来的401 s降低到了241 s,降低了39.9%。由以上数据可得知,实行线控绿波方案后,可以有效提升交叉口通行效率。

4 结束语

干线绿波交通协调控制能够提高城市交通路网主干线的通行能力和服务水平,通过进行信号协调联动控制减少路网中平均排队长度、延误以及行程时间,间接地提高了交通安全性并减少空气污染[7-10]。通过对线控研究的不断深入,我们还可以进行面控,即将绿波协调控制应用在整个路网,以达到更高效率地缓解城市交通拥堵问题。