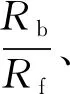液体薄膜的反常过滤性能研究

孙雨欣,毕辛仪,翟世龙,杨超舜,侯泉文,尹剑波

(西北工业大学 物理科学与技术学院,陕西 西安 710129)

物质的分离与过滤被广泛应用于科学研究、工业生产和日常生活等领域. 由于膜分离对操作环境要求较低,在目前能源与水资源缺乏和环境污染严重的情形下,该技术备受重视[1],并被广泛应用于污水处理、食品制造以及医疗分析等多个领域. 根据可分离的颗粒大小,可将主要的膜过滤方式分为:微滤(MF)、超滤(UF)、纳滤(NF)和反渗透(RO)[2]. 影响传统固体膜分离性能的主要参量是膜的结构及其表面特征(如亲疏水性、膜孔径大小以及孔径分布等),这些参量的选择和优化会受工艺水平的限制. 此外,一般情况下传统膜制备出来,膜孔径随之固定,灵活性较差. 其过滤原理一般为:允许小尺寸颗粒通过的同时截留大尺寸颗粒. 然而,当需要通过大颗粒而截留小颗粒时,这种过滤技术将不再适用. 近年来科学家受生物膜内吞作用和液体自愈特性的启发,在固体材料中加入液体材料,使膜技术有了一定突破[3-4],但完全由液体制备的膜过滤器的研究还相对较少.

在日常生活中如在肥皂膜插入1根木棍,缓慢移动木棍时肥皂膜仍可以保持不破裂的状态，取出木棍后肥皂膜会“自动愈合”，这表明了液体材料具有固体材料所没有的特殊性质——自愈性. 基于这一特殊性质，用液体制备出的膜与传统膜过滤器相比拥有反常的过滤性能:允许较大颗粒通过并阻止小颗粒通过,其“膜孔径”可通过调节一些几何参量进行变化. 这一性能使得液膜应用场景更加灵活广泛,如将液膜用于开放性手术[5]、无尘实验室(抑制灰尘等杂质通过,允许较大操作设备通过). 本文将从能量角度出发,结合受力分析建立液膜过滤的理论模型,解释液膜反常过滤性的来源并进行相应的实验验证.

1 理论分析

1.1 膜过滤的球体模型描述

首先以球体粒子建立液膜过滤机理的理论模型. 不同粒子以一定速度落向水平液膜上,如图1(a)所示,一部分通过膜,一部分滞留在膜上,如图1(b)所示.

(a)不同球体落向液膜

对于顺利通过膜的粒子,其通过膜后仍然具有一定的速度,而对于滞留在膜上的粒子在未通过膜前其速度已经减为0. 在与膜接触过程中,粒子是否拥有充足动能,是滞留或通过的关键条件,因此可以从能量转换的角度建立理论模型.

1.1.1 球体滞留的极限位置

考虑可以滞留的临界状态,在滞留位置(v=0)处,若膜对球体的表面张力的合力可以平衡球重力(图2),球可以保持滞留的状态,反之球会获得向下的加速度进而穿过膜,无法滞留.

图2 球滞留在膜上的受力分析示意图

膜与球接触面上的表面张力合力为

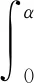
(1)

1.1.2 液膜与球体的能量转换

球体与膜接触时带有一定动能,因此能使膜表面积增加,从而导致膜的内能发生变化.在球体与膜接触过程中,由于液体存在黏性,二者之间的黏性阻力使能量产生了一定的损耗.从球体刚接触膜到球体滞留(v=0)的能量转换关系为

Ek-0=ΔU+Ei,

(2)

其中，Ek为球体刚到达膜处的初动能,ΔU为膜的内能增量,Ei为球与膜接触产生的能量损耗.在本文的实验环境中,Ei数量级为10-8J,Ek和ΔU数量级为10-6J.由于Ei很小,因此可以忽略黏性阻力带来的损耗[6].式(2)可化简为

Ek=ΔU.

(3)

为定量分析,需得到Ek与ΔU的具体表达公式.假设从距离膜高为H处释放重力为G的球体,则对于球体初动能Ek有:

(4)

式中,Rb为球体半径,ρb为材料密度,H为释放高度,g为重力加速度.从热力学角度,在无电磁场等因素影响下,液膜为简单系统.其热力学基本微分方程为[7]

dU=TdS+γdA=CvdT+γdA.

(5)

球体与液膜处在同一环境中,环境温度、压强恒定,因此认为膜过滤的过程为等温过程.液体的表面张力系数γ只是温度T的函数,与表面积A无关[7].膜的初始状态记为(T0,A0),达到极限位置时,膜的状态为终态(T0,A).对(5)式进行积分:

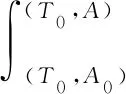
(6)

其中ΔA表示末态与初态的表面积差.(6)式表明膜内能的变化量等于表面能的增量.计算ΔU需得到ΔA的表达式[8]. 文献[5]从最小表面积原理出发,利用边界条件建立方程组,最终求得膜的母线方程为

(7)

(8)

(9)

为对E*中的变量分别进行讨论,对(9)式两端同时取对数得:

lnE*=C+lnγ-lnρb-lnH+

(10)

通过图3可得到以下结论:

2) 随着的γ增大[图3(b)],曲线上移,液膜过滤“孔径”增大;

3) 随着ρb的增大(图3(c)),曲线下移,液膜过滤“孔径”减小;

4) 随着H的增大(图3(d)),曲线下移,液膜过滤“孔径”减小.

(a)ln E*随Rb/Rf变化

1.1.3 lnE*≈0时膜状态的分析

lnE*≈0表明ΔU≈Ek,在膜与直径相切时,小球动能几乎为零,无法迅速穿过膜,而是沿曲线向球与膜的分界线处移动,此时张力无法平衡重力,膜破裂.因此在lnE*≈0时,液膜易破裂,膜破裂时对应的球体直径称为分界直径(即为膜过滤“孔径”).

1.2 一般形状物体

研究过程与球体类似,首先建立物体下落过程膜母线方程,进而求出膜表面积的变化,最终建立物体动能与膜内能的比值关系,对其中变量进行依次讨论即可,这里不再赘述.可将物体大致分为2类: a.表面积连续变化(如球体):截面曲率半径连续; b.表面积有突变(如钉子):截面曲率半径存在突变.

由式(6)可知,膜内能随下落物体与膜接触的表面积的变化而改变.对于球体,其表面积连续变化(截面连续),因此膜内能可连续发生变化至球通过或滞留.但若下落的物体表面积存在突变,由于能量无法突变,因此在物体表面积突变处,膜无法随之变化,容易发生破裂.

2 实验与分析

2.1 实验装置

实验采用一定浓度肥皂水与蒸馏水的混合液制作液膜. 将铁环用不可伸缩尼龙绳固定在3个实验台上,如图4(a)所示,通过调节尼龙绳长度使铁环达到水平状态后固定,如图4(b)所示,将装有液体的水槽与铁环接触,使液体浸没铁环,缓慢移走水槽得到近水平肥皂膜. 实验整体装置示意图见图4(c),利用摄像设备记录实验过程以读取刻度尺上读数. 考虑到透视效应,本文提到的高度H已按照相似关系对刻度尺读取高度进行了换算.

(a)正视图 (b)俯视图(中间为水平仪)

2.2 球膜半径比对膜过滤性能的影响

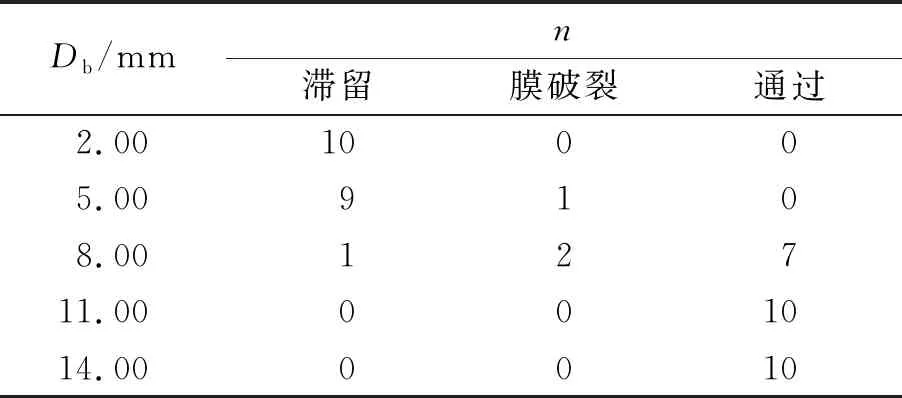
表1 5种小球的实验数据表

通过表1可以发现,小球直径Db处于5.00～8.00 mm的区间时,膜易破裂. 为找到更加准确的临界直径,将该区间细化:以1.00 mm为间隔依次增加Db,每种直径的小球分别进行20组实验. 将实验数据绘制如图5(a)所示.

(a)实验数据

小球直径在Db=8.00 mm附近时,液膜容易破裂(无法快速穿过);Db<8.00 mm,小球滞留次数随Db减小而增大;当Db>8.00 mm,小球易穿过液膜且膜不破裂. 将实验条件代入理论推导式(10)得到图5(b),理论推导得到的分界直径与实验得到的直径基本相符.

2.3 膜表面张力系数对膜过滤性能的影响

实验通过改变肥皂液组分浓度增加张力系数[9]，并采用拉脱法进行测量[10-11],其余实验条件与2.1中保持一致. 使用γ=31.64×10-3N/m与γ=39.22×10-3N/m的2组溶液分别进行实验(小球直径Db:5.00～12.00 mm),分别得到图6的实验数据图.

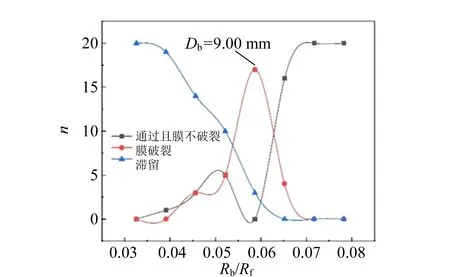
(a)γ=31.64×10-3 N/m

2.4 材料密度对膜过滤性能的影响

使用不同密度的小球分别进行实验,这里使用了聚四氟乙烯(ρPTFE=2.2 g/cm3)、铝球材质(ρAl=2.7 g/cm3)的不同直径小球分别进行多次重复实验(实验参量与图5相同),PTFE球实验结果见表2，铝球全部通过膜.

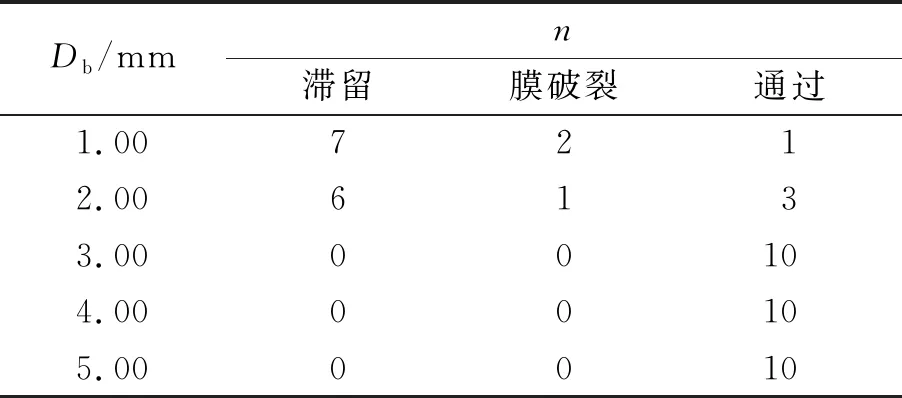
表2 PTFE球实验数据表

受实验条件影响,无法对直径小于1.00 mm的球体进行实验. 在现有实验条件下铝球未出现分界直径,PTFE球在1.00 mm附近可能出现分界直径. 实验2.4所用材料与2.1～2.3中所用材料相比密度增大. 通过实验可知随小球密度增大,液膜分界直径减小,相同直径下，密度大的球体更容易穿透液膜.

2.5 释放高度对膜过滤性能的影响

仍然采用控制变量法,从不同高度释放小球(Db=5.00 mm),进行多次重复实验,实验结果如图7(a)所示,由于实验中存在一定的客观因素(如实验台振动、空气扰动等)带来的影响,使实验中存在1次偶然结果(如图中曲线的“双峰”),但曲线的整体趋势仍符合理论分析. 随着释放高度的增加,球体通过次数显著增加. 膜的过滤“孔径”随H的增加而减小,这种性质与一般的固体膜过滤不同. 对于固体膜,一旦制造出来,其过滤孔径将保持不变. 利用液膜这一特征可以筛选出具有某一速度的颗粒. 在该实验参量下(Df=153.40 mm,Db=5.00 mm,ρ=0.105 4 g/cm3, γ=26.43×10-3N/m)对应的理论计算结果见图7(b). 从图中可以看出理论预测的临界释放高度与实验基本吻合.

(a)实验测量数据

2.6 不同形状物体对膜过滤性能的影响

利用不同形状的物体截面图及释放方向如图8所示,分别从同一高度释放,进行多次反复试验，得到实验结果见表3.

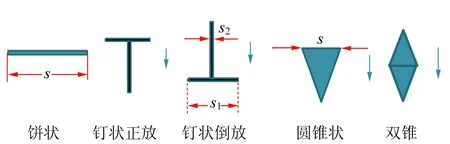
图8 不同形状截面图

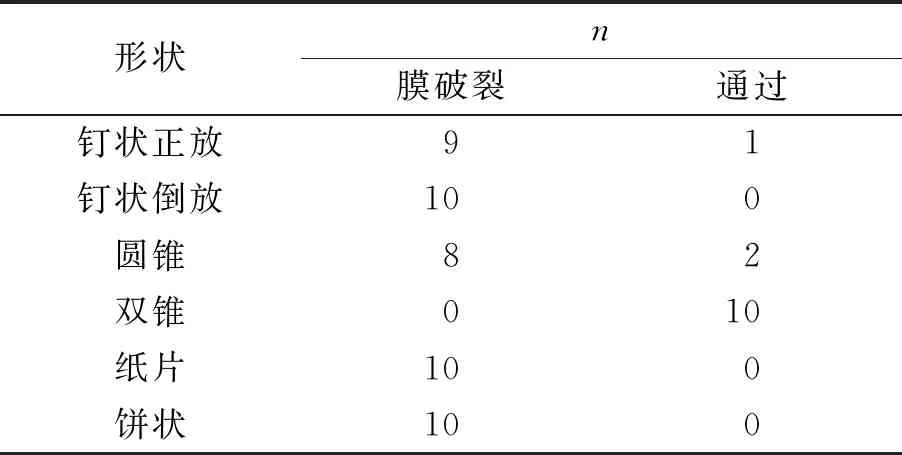
表3 不同形状物体实验数据

实验结果表明：钉状、饼状、圆锥状物体通过膜时,膜易破裂,相同条件下双锥状物体则可以顺利通过膜. 值得指出的是,即使是重力很轻的饼状(纸片)也会引起膜的破裂. 通过图8可以看出几种形状物体通过液膜时，液膜横截面积的变化情况,对于饼状物体与膜接触时，液膜横截面积为S,但穿过后横截面积会突变为0,钉状物体通过液膜时，液膜横截面积虽不会突变为0但也会发生剧烈变化,圆锥状物体在全部通过液膜时，液膜横截面积也会由S突变为0. 而对于双锥状物体,液膜横截面积始终连续变化,因此可以顺利通过. 由上可知,膜的完整性受过滤物体形状影响,对于横截面积突变的物体会导致液膜破裂.

3 结 论