利用电磁阻尼单摆测量金属球的电导率

钟旭英，张朝晖，唐东升

(1.湖南师范大学 物理与电子科学学院，湖南 长沙 410081; 2.北京大学 物理学院,北京 100871)

单摆运动是生活中常见的运动，也是物理学研究中的重要模型，在理论及实验教学中都有着重要的地位[1-2]. 中学阶段考虑的单摆运动是抽象成简谐振动的理想模型，但是随摆动时间逐渐积累单摆实际上是振幅随时间不断衰减的阻尼振动. 生活中可以利用阻尼解释很多物理现象，如各类机器的防震器中采用一系列的阻尼装置，通过改变阻尼的方法控制系统的振动情况；一些精密的仪器，如物理天平、灵敏电流计中也装有阻尼装置，并通过调整阻尼状态，可以使测量快捷、准确. 相关文献对空气阻尼进行了研究报道，例如通过单摆测量空气的阻尼系数[3-4]和黏度[5]等.

电导率是表征金属材料性能的重要物理量之一，可用于分选材质、确定金属材料的硬度和热处理状态. 目前金属电导率的测量方法有很多[6-7]，一般是通过直接测量金属丝的直径、长度和电阻，代入电导率的公式计算金属的电导率. 因此通过在单摆实验加入梯度磁场，让2个大小相同、电导率不同的金属球在梯度磁场中做小角度摆动，然后对空气阻尼和电磁阻尼展开定量的研究，采用对比法测量金属球的电导率.

1 基本原理

1.1 单摆系统线性阻尼振动方程的解

忽略阻尼情况下，单摆可以抽象成简谐振动的理想模型. 弱阻尼情况下，空气阻力对单摆振幅的影响随摆动时间逐渐积累，从而使得摆幅随时间逐渐衰减. 如图1所示，当小球摆动的速度很小时，空气阻力近似与摆球速度成线性关系，此时小球的运动称为线性弱阻尼振动. 根据牛顿运动定律可以得到单摆系统的动力学方程为

图1 单摆在空气中的线性阻尼振动

(1)

式中：m为摆球的质量，l为摆线长度，γ为阻力系数，θ为摆球的摆幅，g为当地重力加速.

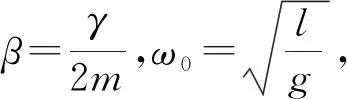
(2)

该方程的解与阻尼系数有关.

当β<ω0时，系统处于弱阻尼状态，其解为

θ=θ0e-β tcos (ωt+φ0),

(3)

当β=ω0时，系统处于临界阻尼状态，其解为

θ=(C1+C2t)e-β t,

(4)

此时系统不做往复运动，而是较快地回到平衡位置并停下来.

当β>ω0时，系统处于过阻尼状态，其解为

(5)

此时系统不做往复运动，而是非常缓慢地回到平衡位置.

1.2 运动金属球在梯度磁场中受到的电磁阻尼力

梯度磁场指的是空间变化率不为零的磁场. 金属球在这样的磁场中运动时会在其内部产生感应电动势，从而产生涡旋电流. 在本文的实验中，摆球位于以平衡位置为中心向左右两侧线性减弱的梯度磁场，两侧的磁场梯度为大小相等、方向相反的常量. 当摆球从中心向右摆动，其产生的感应电流如图2(a)所示. 在涡流和外磁场的作用下，金属球受到4个方向的等效作用力如图2(b)所示，这些作用力的合力总是与金属球的运动方向相反，故称之为电磁阻尼.

(a) 垂直磁场方向观测到的感应电流(紫色虚线表示磁感应强度)

Adom Giffin[8]等人对金属球在梯度磁场中做低速运动时受到的电磁阻尼与金属球的电导率的关系展开研究，在忽略磁场扰动对电磁阻尼影响的情况下，得出金属球在梯度磁场中做低速运动时，其线性弱电磁阻力表达式为

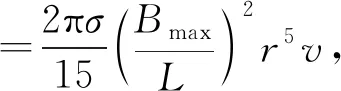
(6)

其中，r是金属球的半径，v为金属球的运动速度，σ为金属球的电导率，Bmax为最大磁感应强度，L为梯度磁场的宽度.

1.3 求解金属球的电导率

空气阻尼为：

(7)

摆球在磁场中振动受到的阻力为

F阻=F空+F磁，

(8)

联立(7)(8)两式得：

F磁=F阻-F空=(γ阻-γ空)v，

(9)

由于阻尼系数γ=2mβ，代入(9)式，与(6)式联立解得电导率为

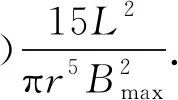
(10)

因此在有无磁场阻尼作用下，通过测定大小相同，电导率不同的2个金属球的阻尼系数，再采用对比法即可得出待测金属球的电导率为

(11)

2 实验仪器及步骤

2.1 实验仪器

1) 单摆装置：包括半径为90 cm的测角仪，量程为-5.5°～+5.5°，分度值为0.1°(见图3)；

2) 带摆线的铝球(质量m=11.346 g、半径r=10.000 mm、电导率σ=3.767×107S/m)；带摆线的待测金属球(质量m=35.112 g、半径r=10.000 mm)；

3) 螺旋测微器、卷尺、多通道计时秒表(精度为0.01 s)；

4) 钕铁硼永磁铁(20 mm×20 mm×10 mm).

2.2 实验步骤

1) 按照图3所示，将铝球作为单摆的摆球，调节铝球的摆线长度为95.00 cm.

图3 单摆在磁场中的阻尼振荡

2) 让铝球做小角度(θ≤5°)摆动，当摆球摆到最低点时，用多通道计时秒表记录摆球摆动n次的时间，并记录摆幅随时间变化的实验数据.

3) 不改变摆球及其摆线长度的情况下，将钕铁硼永磁铁放置于铝球平衡位置正下方大约x=2 cm处. 让铝球做小角度摆动，记录摆幅随时间变化的实验数据.

4) 用待测金属球替换铝球，保持磁铁的位置不变，调整摆线的长度使其与原铝球摆线长度一致.

5) 让待测金属球做小角度摆动，记录摆幅随时间变化的实验数据.

6) 移开磁铁，让待测金属球做小角度摆动，记录摆幅随时间变化的实验数据.

3 实验结果

3.1 磁铁位置分析

本文使用的2个金属球质量和电导率存在较大的差异. 与待测金属球相比铝球较轻，则铝球摆动过程中，空气阻尼和电磁阻尼对其振幅的影响较大，而对待测金属球的影响较小. 要想在有限的时间内缩短测量时间的同时得出更准确的测量数据，则磁铁的位置至关重要.

3.1.1 磁铁位于摆球平衡位置正下方的分析

本文的钕铁硼方形磁铁放置于摆球平衡位置正下方，其目的是在摆球平衡位置形成对称分布的梯度磁场. 为此本实验使用特斯拉计测定摆球振动轨迹对应的磁场变化情况，如图4所示. 测量结果表明磁感应强度(B)随摆幅(θ)的增大而减小，从图4中可以发现钕铁硼磁铁形成的实际磁场是理论要求“等腰三角形”分布的近似，满足电磁阻尼力磁场理论的要求.

3.1.2 磁铁与摆球质心距离的分析

本文选择摆长为96 cm，对应的周期T约为1.97 s. 磁铁距离摆球越远，单摆在磁场中运动的振幅衰减越慢，可采集到摆幅的数据点就越多，拟合的阻尼系数越准确. 并非是磁铁距离摆球越远越好，磁铁太远会增加测量时间，太近则较轻的摆球摆幅衰减太快，不利于实验数据点的采集. 况且本文并非仅考虑单个摆球振幅的衰减规律，而是需要综合考虑2个摆球的质量和电导率对摆幅衰减快慢和测量数据点数量的影响，这就需要找到合适的位置，所以磁铁在平衡位置与摆球质心的距离也是完成本实验的关键因素之一.

实验发现记录1个摆幅数据点至少需要2个周期的时间即3.94 s，因此摆幅从5°衰减到2°，采集获得11个数据点，则在平衡位置磁铁距离摆球的质心至少应为2.5 cm. 实验发现每隔5个周期记录1个摆幅时，时间相对充裕，能更准确捕捉到摆球摆到最高位置的角度，测量更准确. 根据实验结果每隔5个周期记录1个数据需要9.84 s，让幅度从5°衰减到2°采集11个数据点，在平衡位置磁铁距离摆球质心则约为3 cm. 综上本文所使用的平衡位置磁铁距摆球质心位置为3 cm.

3.2 阻尼作用对振动周期的影响

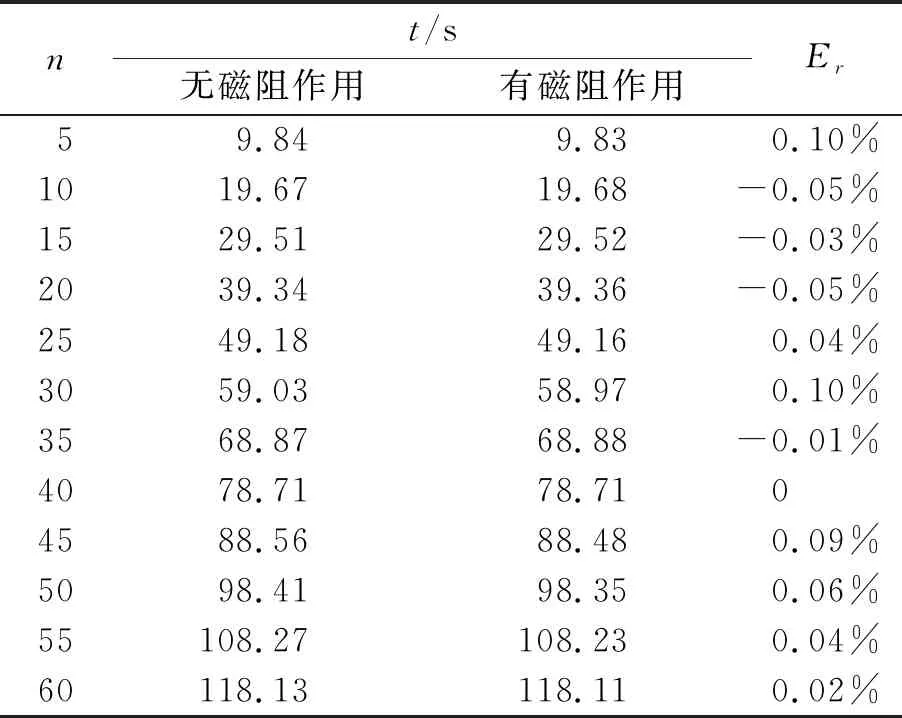
表1 摆球在有无磁阻作用下周期-时间表

3.3 实验数据处理

由于单摆在有无电磁阻尼作用下的阻尼系数远小于单摆的固有周期，所以无法通过测量周期计算出单摆的阻尼系数. 根据弱阻尼振动微分方程的解[见式(3)]，可知单摆的振幅随时间呈指数衰减，本文通过提高摆幅测量的精度(见图3中测角仪的放大图)，测定单摆摆幅随时间的衰减规律，利用θ=θ0e-β t进行拟合得到摆球在有无磁场作用下单摆振荡的阻尼系数β，如图5所示. 结果表明单摆在摆动过程中摆幅随时间呈指数衰减，实测数据与拟合结果吻合得很好. 实验结果证实2种金属摆球在有无电磁阻尼作用下，阻尼系数β(详见图5)都远远小于单摆的固有频率ω0=3.19 s-1，故阻尼对单摆振动周期的影响可以忽略不计. 单摆的阻尼系数可以通过测量单摆摆幅随时间的衰减规律来求解.

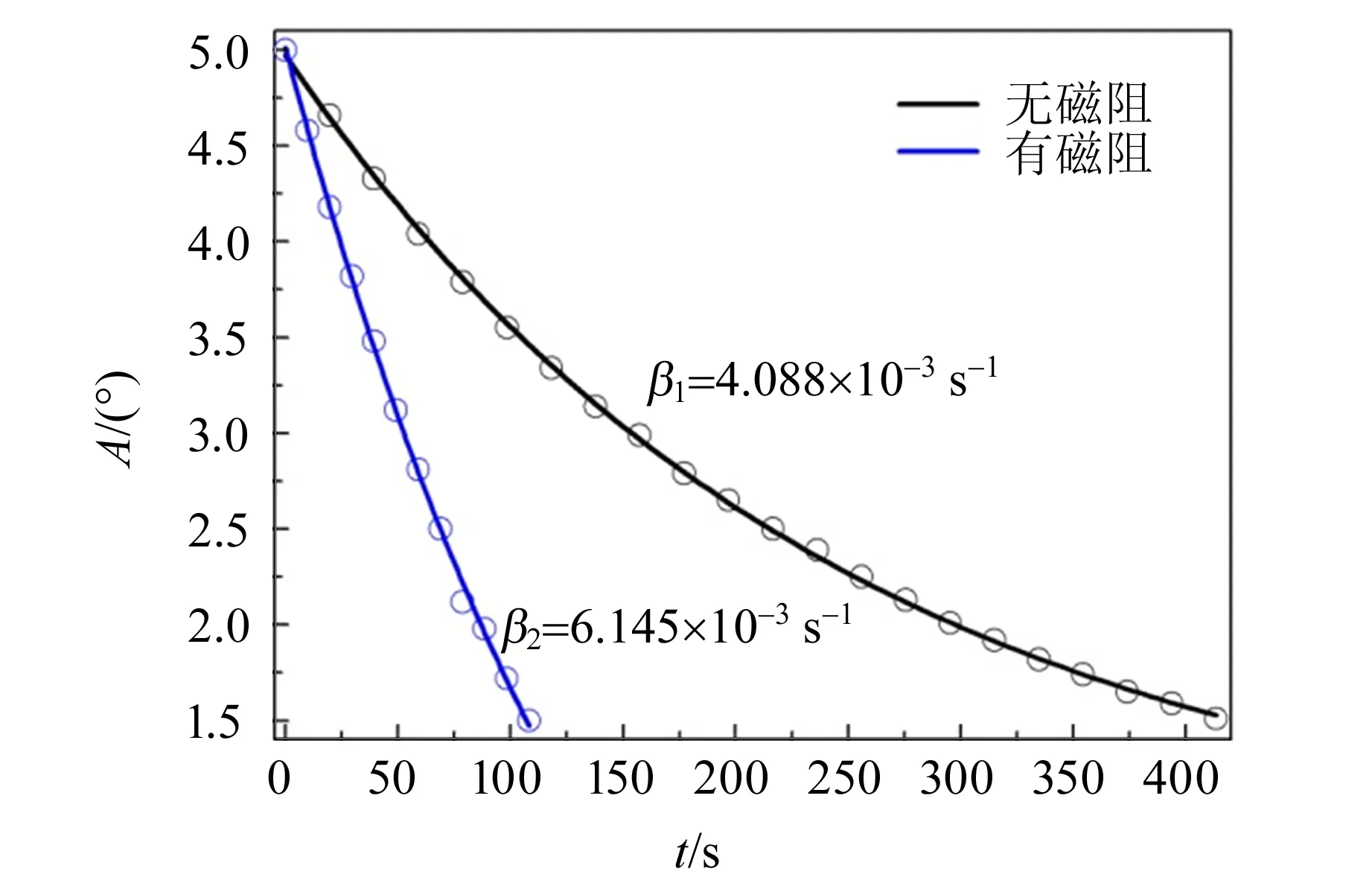
(a)铝球作为摆球

3.4 对比法求解金属球的电导率

根据图5曲线拟合的结果和已知条件，待测金属球：m1=35.112 g，β1阻=1.557×10-3s-1，β1空=1.506×10-3s-1；铝球：σ2=3.767×107S/m，m2=11.314 g，β2阻=6.165×10-3s-1；β2空=4.070×10-3s-1.

将所有的已知条件代入式(11)求得待测金属球的电导率σ1=2.86×106S/m. 其中r1=r2.

实验结果表明待测金属球的电导率与相关资料提供的锰铜电导率的数据(σ=2.78×106～3.23×106S/m)相匹配. 本文使用的待测金属球的密度ρ为8.38 g/cm3和锰铜的密度相近. 同时本实验累计测量n次摆幅随时间的衰减规律，得到n个阻尼系数，电导率的不确定度为uσ1=0.14×10-6S/m

4 结束语

本文利用简单的力学单摆实验，采用对比法测量电磁学的物理量，定量研究了空气阻尼和电磁阻尼. 通过观测2个大小相同、电阻率不同的金属球在有无电磁阻尼作用下摆幅随时间的变化规律，拟合实验数据得到空气阻尼系数和电磁阻尼系数，采用对比法可得出待测金属球的电导率. 实验结果表明，利用单摆小角度的弱阻尼振荡，结合金属球在梯度磁场中运动时受到的磁阻尼力求解金属球电导率，方法可行. 该实验可加深学生对单摆作为简谐振动理想模型的理解，另一方面也为研究梯度磁场中金属小球的电磁感应现象提供了新思路.