冶金企业静止无功补偿方法研究

赵乘康，范 佳，郭进喜

（1.河钢集团邯郸钢铁设计院有限公司，河北 邯郸 056000；2.河钢集团邯郸公司技术中心，河北邯郸 056000；3.河北工程大学机械与装备工程学院，河北 邯郸 056000）

随着多种新型电力电子设备投入冶金企业，其非线性、冲击性、不平衡的特征使得负荷更趋复杂化和多样化，同时带来的还有更为严峻的无功功率不足问题，在降低了电能质量的同时，给供配电系统提出了更高的要求。

冶金企业配电和负载有其特殊性，其中感性负载的占比较重，例如三相交流异步电动机、吊车、电焊机、交流接触器以及大量需要电感器启动的照明设备等。这些功率因数较低的设备在运行中将带来一系列不良后果，包括增加电能损耗、线路中的电压损失、供电质量降低、发供电设备的利用率低以及发电成本升高等。因此准确的无功功率补偿容量计算以及更适用于冶金企业的无功功率补偿方法显得尤为重要。

无功功率补偿和优化历来是电力系统的重要研究内容。由于冶金企业负载的复杂性，其无功功率补偿是一个涉及多变量和多约束条件的规划难题，如何采用合理的无功功率补偿容量计算方法以及寻找一种合理的无功功率补偿方案，并在合适的运行点使用科学的补偿装置，以实现最合理的投资和运行状态，是本文主要的讨论内容。

1 无功补偿装置必要性

如图1所示，此为电力配电系统示意图，而无功功率平衡是保证电力系统电压质量的前提。现在保持同步发电机端电压不变的前提下，对受电端和送电端功率平衡关系进行分析：

图1 送、受端示意图

受电端：

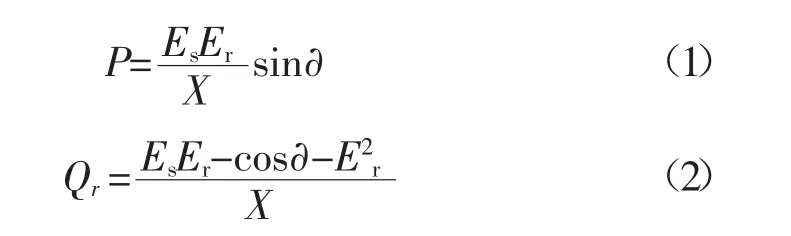
式中：P为有功功率；Es为送电端电压；Er为受电端电压；∂为功率因数角；X为电抗；Qs为送电端无功功率；Qr为受电端无功功率。

送电端：

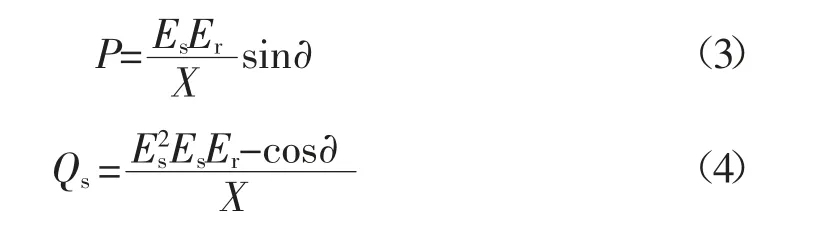
受电端和送电端的无功功率：

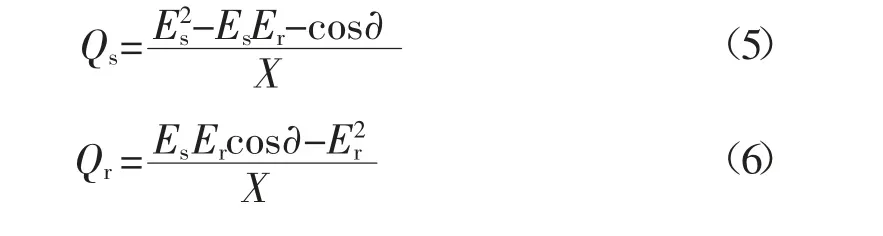
如果仅仅考虑输电线路的无功功率，用V s代表送电端的电压，V r代表受电端的电压，X代表输电线路电抗，对公式进行如下变化：

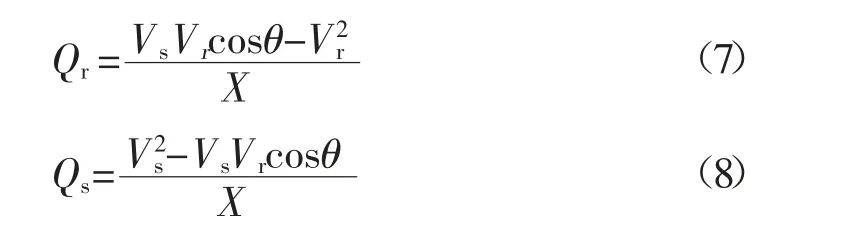
假设cosθ=1，带入方程近似计算得出表达式：

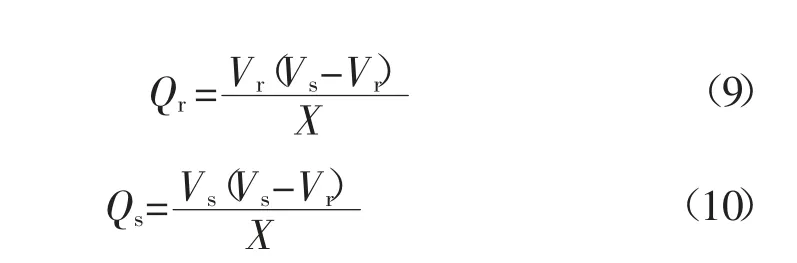
通过对上述公式进行分析可知，传输无功功率的大小主要会受到电压幅值和传输线路的电抗影响，方向为由电压高的一端流向电压低的一端。其传输过程中的无功功率损耗，为：

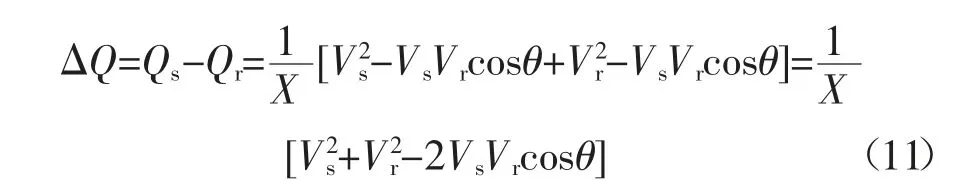
将送电端无功功率作为基准，进行损耗比率计算，则电抗传输后无功功率损耗比率为：

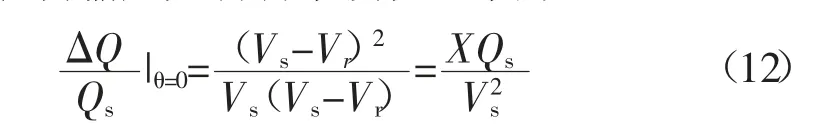
由上述公式可以分析得到，随着传输距离的增加，无功功率损耗也将增加，并且成正比关系。传输的无功功率越大，无功功率损耗也越大，并成正比关系。电源电压过低也将导致无功功率损耗增大。无功功率过大，将会使得电网中总电流增加，这将造成设备和线路的损耗变大，变压器承受的电压损失也越大。而无功功率的补偿，使得功率因数提高，减小系统的实际功率，从而减小电网中所有设备容量，降低了电网的投资成本。

2 无功补偿容量计算方法

2.1 电缆无功功率补偿容量计算

冶金企业本身特点决定了在企业内部的线路多用电缆的传输方式。相比较于架空线路，电缆的阻抗较小、可靠性高。但同时电缆拥有较大对地电容效应，在交流电压作用下将产生容性无功功率，即对系统产生无功充电功率，不利于电网的安全稳定运行。因此非常有必要将电缆充电功率对系统的运行影响进行分析，电缆无功功率补偿容量计算如下：

电缆线路的π型等值电路如图2所示：

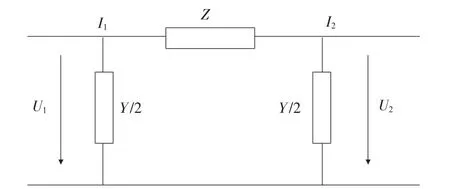
图2 线路π型等值电路示意图

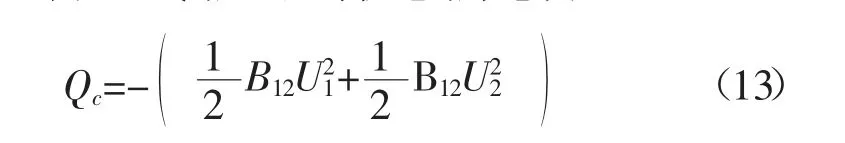
式中：Qc为线路的充电功率；B12为线路对地电纳；U1、U2为线路两端电压。

由公式（13）可知，电缆的充电功率与电缆的对地电纳的大小及电压等级的平方成正比。实际的工程计算中一般采用如下公式。

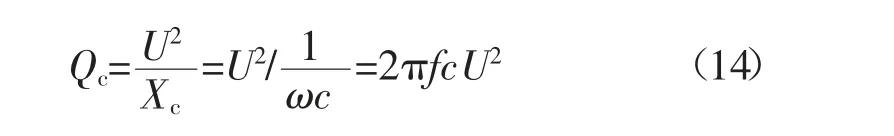
式中：Qc为线路充电功率；Xc为电缆等值对地电容的电抗值；U为电缆等效电压，在近似计算中可采用供电母线电压。

由公式（14）可以分析得到，电缆充电功率与电压等级、电缆对地电抗值有关，其中电缆电抗值大小与电缆截面积有关。

电缆充电功率补偿后变压器高压侧的功率因数cosφ计算如下：

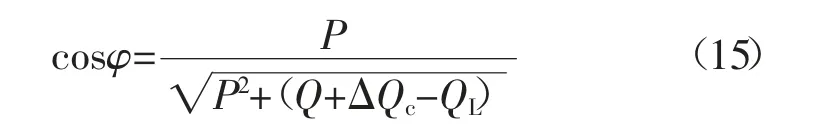
式中：ΔQc为电缆充电功率；QL为低压侧补偿容量。

根据式（15）可以得出低压无功补偿容量计算公式如下所示：

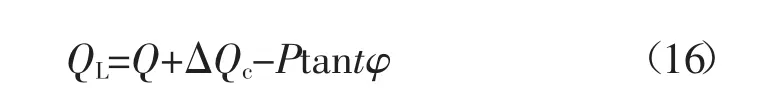
在交流电压系统中，电缆的对地电容效应将产生无功充电功率，需在系统相关线路节点进行无功平衡计算，并提供合理的无功功率补偿装置。

2.2 负荷无功功率补偿容量计算

在计算负荷无功功率补偿容量计算时，通常是通过补偿前平均功率因数（自然平均功率因数）和补偿后平均功率因数来进行。具体计算公式如下：

补偿前平均功率因数为：

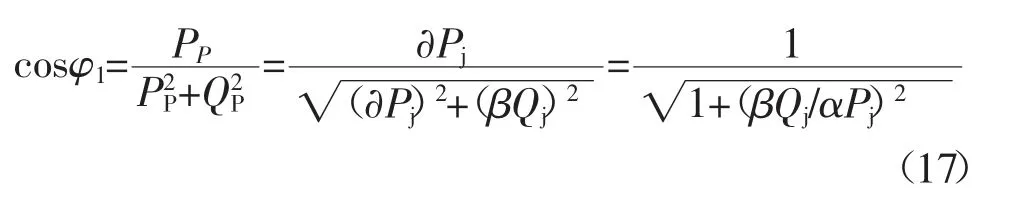
补偿后平均功率因数：

即无功功率补偿器容量由下式确定：

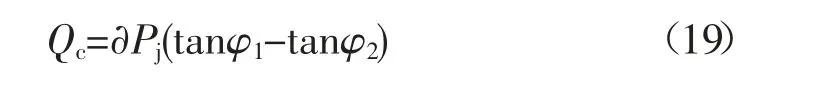
式中：Pj、Qj分别为负荷有功功率和无功功率；PP、QP分别为平均有功功率和无功功率；∂、β分别为平均有功负荷系数和无功负荷系数。

需要注意的是，在工业企业实际运行过程中，一般不会满负荷工作，所以计算过程中一般采取平均功率计算，不会进行最大功率计算，在避免出现过补偿现象的同时，降低初投资。

在进行系统无功功率补偿计算时，需要考虑电缆和负荷的无功功率整体的补偿容量。根据不同节点自身的特点和情况，以及未来规划预留情况，进行分析计算，才能得到更为科学的计算容量，避免过补偿或者欠补偿的情况发生。

3 无功补偿方案选择

目前主要的无功功率补偿方法有静止无功补偿和动态无功补偿两种。其中静止无功补偿装置又包括饱和电抗器静止无功补偿装置（SR）、晶闸管投切电容器（TSC）、晶闸管控制电抗器（TCR）以及高级静止无功发生器ASVG等。相对静止无功功率补偿装置的动态无功功率补偿装置在电压、电流的采样原理上与静态无功功率补偿装置是一样的，其主要区别在于输出控制电容投切的电路部分。

针对冶金行业的负荷通常具有冲击性和波动性等特点，同时非线性负荷在企业中的应用也在日益增加，比如，吊车、轧机、焊机、电梯等，提出了一种将TCR（晶闸管控制电抗器）和TSC（晶闸管投切电容器）进行结合的一种可靠、经济的SVC补偿方案。

TCR补偿装置通常分为6脉冲和12脉冲两种形式。一般设计中TCR只吸收无功，可通过并联电容器实现容性到感性无功功率的调节。其具有反应速度快、控制灵活性高的特点，并且可以将不同控制策略，比如外部辅助信号控制，加入TCR中实现，这样可以大大提高系统的整体性能。其模块化设计的特点使得扩容设计变得很简单，只要不超过电压器容量，增加TCR模块就可完成扩容。

表1中显示了常用的TCR、MCR、TSC的主要性能对比，其中TCR和MCR具有连续无功功率输出的能力，而TSC则能够阶梯输出。TCR拥有限制过电压能力，并且能够吸收一部分谐波。而TSC的损耗率相对其他装置有明显的优势的。

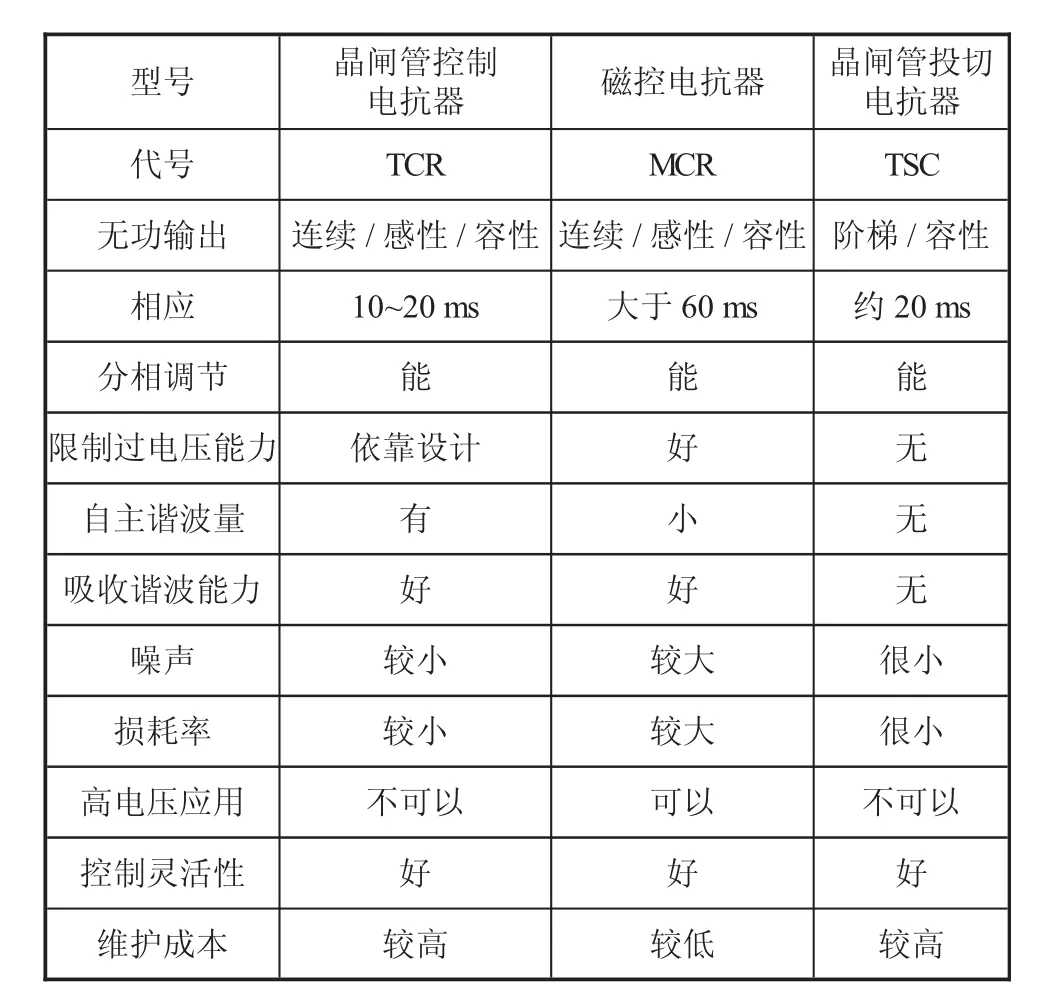
表1 TCR、MCR、TSC特性对比

根据以上无功功率装置的对比，结合冶金企业配电和负载特点，提出将TCR与TSC相结合的SVC无功功率补偿装置。这样既可以实现更优的无功功率补偿效果，降低电网损耗的同时提高电压质量，并且在经济上也具有一定的优势。

4 仿真分析

4.1 仿真模型建立

电压水平是衡量无功功率平衡的一个主要内容，通过电压的稳定性来显现无功功率补偿的过程为此次仿真模型的目的。

此次仿真建立的模型为一个TCR和一个TSC配合构成的SVC模型，这也是在工程实际应用中最为简单常见的组合方式。其中TSC可以是一个大容量电容器，也可以是一组小容量电容器，在相同总容量的前提下，组数越多，补偿的效果和精度也就越好，但是其成本也越高。因此，在实际应用中需要找到一个电容器组数和补偿精度的平衡点，得到最佳的配比关系。

TSC通过开合晶闸管，可以控制电流流过电容，因为其电压滞后电流，从而可以提供感性无功功率，属于有级调节的粗调。TCR则是通过调节导通角，从而控制电流流过电感，当其电压超前电流90度，也就是纯电感时，与TSC相反完成吸收感性无功功率的功能，可做细调，由于导通角可以连续变化，因而其吸收无功功率也是连续的。

仿真模型主要包括控制部分（使用PI控制器）、电源、变压器和负载。由三相电源负载供电，SVC通过变压器低压侧进行补偿，最终达到稳定电压的目的。

4.2 仿真结果及分析

MATLAB软件中仿真实验参数设定：

Ki为800，TSC组数为1，容量为0.94（基准值为100 MVA）

仿真结果见图3。

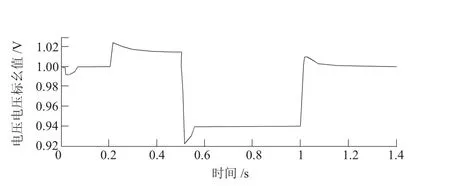
图3 仿真图

从图3可以看出，在0.2 s时，电压设定变化为1.025 V，无功功率补偿装置需将电压降低。此时TSC并没有投入，TCR导通角立刻响应，在0.4 s时，将电压稳定在1.015 V，耗时0.2 s，补偿0.01 s。在0.5 s时，电压设定变化为0.93 V，TCR导通角立刻响应，而在0.525 s时TSC才开始投入，有0.025 s延时，电压恢复过程有轻微震荡，最高最低振幅差值为0.015 V，在0.78 s时，电压稳定在0.955 V，耗时0.28 s，补偿0.03 s。在1.0 s时，电压设定为1.0 V，但电压突升到1.03 V，TCR和TSC共同响应，电压稳定在1.001 V，耗时0.12 s，补偿0.029 s。

分析可得，TCR和TSC配合使用的SVC无功功率补偿方案可以快速、准确的完成补偿过程，并且可以实现功能上的互补。需要注意的是，当TCR和TSC装置共同投入时，会有一段时间不稳定状态，也需要一定的响应时间作为缓冲。

5 结语

1）阐述了冶金企业无功功率补偿的重要性和必要性。

2）介绍了电缆和负载无功功率补偿容量计算方法，强调在无功功率容量计算中需要充分考虑节点的自身情况。

3）根据不同补偿装置的特点，提出将TCR和TSC补偿装置相结合的SVC补偿方式应用在冶金企业中。

4）构建TCR和TSC补偿装置相结合的SVC仿真模型，在MATLAB环境下进行仿真分析，结果也印证了其可行性。