基于混合粒子群的建筑电气三维自动布线设计研究
傅军栋,熊红亮,杨 娜,谈永胜,刘 珺
(华东交通大学电气与电子工程学院,江西 南昌 330013)
目前大多数建筑电气设计还是在二维图纸上进行布线设计, 二维图纸的各类建筑结构复杂,设计者容易出现布线交叉、穿墙布线、误读标准及规范等问题,造成多次改图,造成建筑电气设计周期过长,且降低图纸设计施工的可读性,无法满足建筑建设要求;同时为响应政策号召,提高图纸的可视化和施工可靠性及加快建设建筑信息管理,应用建筑信息模型(BIM)进行设计施工已逐渐成为行业趋势。 在搭建好的三维建筑模型内,专业的设计人员根据相应的规范条例进行电气系统设计,主要包括照明系统和动力系统的设计,依次完成电气元件的坐标放置以及数量核算后,手动将各电气元件和模块连接形成完整回路,最后完成整个设计过程。
针对三维建筑环境下的布线设计,现有的主要方法有二维翻模法和三维正向设计法。 二维翻模法是在二维图纸上进行布线设计后翻模成三维建筑电气图纸,工作量大且容易造成信息遗漏,设计效率低下造成设计周期过长[1]。 三维正向设计法是结合三维建模软件在三维模拟环境中直接进行布线设计,以实现让计算机取代人为手动布线[2]。 在已知电气设计设备的数量及坐标的前提下,三维建筑内的电气布线优化问题可视为一个三维环境下的路径优化问题的扩展, 一些学者已对此进行探索研究。 杨光育等[3]提出了一种基于CATIA 软件的自动三维布线设计模型,不过需要调用预先设计好的接线表和器件表来模拟布线。文明等[4]结合Pro/E 软件开发了一个基于路径控制点的实现简单布线的辅助布线系统,但仍需通过手工点击位置来选取路径控制点。 蔡毅等[5]提出了以UG 为开发平台的“按面自动布线”生成三维电气线路方法,实现了路径自动生成、干涉检查及自动调整,但其要人工预处理确定布线过渡点。 另外还有一些学者对三维环境下的自动布线进行了算法上的研究,如刘武[6]和郑晓芳[7]提出了能够实现配电箱到电气设备以及电气设备之间自动布线的蚁群算法,杨超杰等[8]提出了用于三维空间规划的自适应混沌粒子群优化算法,刘佳顺等[9]和刘潇等[10]针对三维环境提出了基于任意时间的RRT 算法,吴保胜等[11]提出了适用分段式三维空间的基于重力规则的蚁群算法,王长涛等[12]针对三维建筑管道布置提出了自适应模拟退火粒子群算法,董宗然等针对船舶管路布局空间设计提出了最短路径快速算法[13]、基于协同进化和并行计算的A* 算法[14]、改进型遗传算法[15],姜康等[16]提出了针对复杂布线空间的改进A*算法。然而,以上这些研究的算法均未完全实现自动布线,所应用的空间模型并不完全适用三维建筑模型,未考虑电气开关及实际施工的线路问题,未解决建筑内多电气设备的回路连接问题和路径最优问题,仍需要设计人员手动调整线路。
本论文为解决三维建筑模型内的电气自动设计问题,针对电气回路设计可能出现的问题进行了分析,建立了一个满足经济约束、安装约束、物理约束和规范约束的数学模型,并提出了一种结合回路划分策略的混合粒子群算法,对模型和算法的可行性进行了验证,并结合实际设计要求,对安装约束中的弯头函数进行改进以提高算法的收敛速度。
1 数学模型的建立
1.1 电气布线的内容及过程
建筑电气设计的内容一般分为强电和弱电的布局设计, 强电设计包含照明系统的灯具回路连线、动力系统的插座布局回路连线;弱电设计包含综合布线系统的网络回路布局、有线电视系统回路布局。 设计院常见的电气布线系统为强电系统,而弱电配电箱与强电配电箱分开,且要求不一,所以本论文不涉及弱电系统的布线设计内容。
三维建筑中的人为布线设计流程:第一,需要定位出各电气设备的实际三维坐标, 包括灯具、插座、强电配电箱的坐标;第二,根据三维建筑环境的空间属性及电气设备的特性去划分电气回路;第三,进行规范校验,对不符合规范的回路进行重新布线;第四,在回路节点上设置开关并标注导线数结束布线。
1.2 布线模型的设定
为实现上述自动布线功能,且为相类似的建筑类型作参考, 本文选定的建筑空间类型为办公建筑,其常见的房间类型包含办公室、会议室、走廊、卫生间,建筑结构包含承重墙、普通墙、门、窗,电气设备包含各类灯具、插座、开关以及配电箱。
三维建筑内的布局空间结构多样化,为降低模型的复杂度,提高算法效率,从而更直观的研究布线模型,需要对环境空间及设备简化。 本论文选定某一办公建筑标准层作为三维模型,将电气设备中各类灯具的形状统一表示为三维空间中的半径为r1的球体,灯具回路中的开关统一使用单联双控接线方式,故不表示在模型中,插座统一表示为边长为a1的球体,配电箱表示为边长为a2的正方体,以上中心坐标均为其原空间坐标的重心坐标,空间坐标系使用笛卡尔坐标系。 在此布线模型中由于布线不经过窗户,故将窗户所在墙视为承重墙区域。
1.3 目标函数的建立
三维建筑内的电气回路布线设计可视为一个不定起点的路径规划问题, 回路的起点设置不固定,回路终点均为配电箱,回路设计目标为经过的路径距离最短,同时区别于一般的空间三维路径规划,建筑布线模型要求沿墙贴面敷设,布线路径尽量少弯头,回路不能直接穿越墙体及窗口等建筑结构障碍,其受到更多的约束条件限制,如经济约束、安装约束、物理约束、规范约束等,为更好解决电气回路布线问题,本文依次将上述约束数学化。
本文的经济约束主要为布线路径总长度最短,即用线量最少。 将该约束数学化,回路路径总长度可表示为L,灯具回路可表示为D={d1,d2,d3,…,dn},则灯具布线路径长度可表示为L(D),如式(1),l(di,di+1)为灯具回路上相邻节点的欧氏距离之和,如式(2),(xi,yi,zi),(xi+1,yi+1,zi+1)分别为灯具节点di和di+1坐标。

为保证可靠性和施工便捷性的要求,在设计布线回路时,需要考虑施工安装情况,弯头的存在会导致施工工艺复杂,工期增加。 故布线回路中的弯头数量越少,施工越便捷,安装约束可表示为路径中的弯头数。 为方便计算布线回路的弯头数,本文根据偏移角度θ 来判断弯头的存在,回路路径总弯头数可表示为W, 则灯具回路弯头数可表示为W(D),如式(3);w(di-1,di,di+1)为节点di-1和di+1之间的弯头数,由当前节点di及其前后两节点di-1和di+1的偏移角度θ 与弯头角度θ1判断,θ1一般大于2π/3,如式(4)和式(5)。

为保证布线回路不穿越或尽量少穿越建筑结构的物理约束性,在布线模型中引入董宗然[14]所提出的能量法,对每段路径能进行能量赋值,当回路需要穿越墙体时,则该段路径所含能力减弱,故需尽可能少穿越墙体,保证回路能经过本房间内所有路径节点后再去连接其他房间内的路径节点。 以房间属性为参考指标,对相邻两个回路节点间的路径进行评价,对应的属性路径RL分为禁行段RP,可行段RF,优势段RS。为量化上述回路需求,当两回路节点所属不同房间类型时,其两者之间的路径属于禁行段RP,其能量值为0;当两回路节点为同一房间类型但不同房间时,其两者之间的路径属于可行段RF,其能量值为1;当两回路节点为同一房间类型且同一房间时,其两者之间的路径属于优势区,其能量值为2。
物理约束可表示为整条回路的能量值,整条回路能量表示为P, 则灯具回路的能量值可表示为P(D),如式(6);p(di,di+1)为回路区间能量值;区间的能量值由相邻两节点di,di+1所在的路径属性LR 决定,如式(7)。

针对建筑的布线回路设计必然要符合相关设计规范和国家标准,使其具有规范性,针对上述办公建筑类型,相关的强电布线回路规范约束有:
1) 办公建筑配电回路应将照明和插座回路分开;
2) 每一回路照明灯具数量不得超过25 个;
3) 每一回路插座数量不宜超过10 个。
根据 《民用建筑电气设计规范JGJ 16-2008》规范约束可知,照明回路和插座回路分开设置,则插座回路可表示为S={s1,s2,s3,…,sm},sm为插座节点,插座回路长度为L(S),插座回路弯头数表示为W(S),插座回路的能量值表示为P(S),公式均同灯具回路表示;同时在灯具回路D={d1,d2,d3,…,dn}中,n≤25,插座回路S={s1,s2,s3,…,sm}中,m≤10。
基于以上问题模型及约束处理策略可知,规范约束和物理约束是刚性约束,必须满足,约束可在优化算法设计中保证;经济约束和安装约束是柔性约束,尽可能得保证其最优,一般作为优化目标来满足。
2 布线优化算法
2.1 回路划分策略
粒子初始化时,一般按照所需要布局的灯具数来确定粒子的维数,但楼层内的全部电气设备不宜设置在同一条回路中, 以防某一电气设备故障时,容易影响到其他设备的使用,故需要设置多条回路以保证设备的稳定性。 不同房间属性的电气设备不在同一回路上,同时考虑规范约束,灯具回路对应的粒子维数n≤25, 插座回路对应的粒子维数m≤10,所以在初始化粒子维数之前需要划分好楼层内的电气回路。
本文利用建筑信息模型中已知的房间属性及其对应的电气设备数来动态划分回路,提出一种基于房间属性的回路划分策略,使得粒子初始化的维数根据回路上的电气设备数确定, 以照明回路为例,某一房间属性下的各房间灯具总数n=∑{n1,n2,…,ni},策略规则如下:
1) 当n≤25 时, 则该房间属性下的回路数h=1,回路的粒子维数n′=n。
2) 当n>25 时,且该房间属性下的存在单个房间内灯具数nx>25,则需将该房间的灯具分为[n/25]+1个回路来布线设计;n 为奇数时, 单个回路粒子维数n˙=[n/([n/25]+1)]或[n/[(n/25)+1]]+1;n 为偶数时,单个回路粒子维数n˙=[n/([n/25]+1)],其他房间的灯具按照规则3)来划分回路及设置回路粒子数。
3) 该房间属性下的单个房间内灯具数nx均小于25 时, 按照单个房间的灯具数由小到大进行排列生成集合H0,对应的回路数h=[n/25]+1。 对于某一回路的灯具数设置, 可依次从集合H0中取出最小的房间灯具数进行累加,使其回路满足规则1)并依次设置下一回路直至集合H0为空。
按照以上回路划分策略,可知回路所包含的房间以及其所包含的灯具数,因而可知单个回路的粒子维数,每个粒子表示一条灯具回路。 插座回路同理可知,其回路划分策略需满足单回路内插座数量n≤10 即可。
2.2 混合粒子群算法
粒子群算法通过跟踪个体极值和群体极值完成极值寻优,虽然能快速收敛,但随着迭代次数的不断增加,在种群收敛集中的同时,粒子也存在陷入局部最优解无法跳出的问题。 混合粒子群算法改变了传统粒子群算法中通过追随极值来更新粒子位置的方法,而是引入了遗传算法中的交叉和变异操作,通过粒子同个体极值和群体极值的交叉和粒子自身变异的方式搜索最优解。
2.3 算法设置
2.3.1 个体编码
粒子个体采用整数编码的方式,每个粒子表示一种经过电气回路内的灯具或插座,例如当回路包含的灯具个数为8,个体编码为[1,2,3,4,5,6,7,8],表示回路由灯具1 开始, 依次经过1,2,3…连接灯具8,最后再由灯具8 连接楼层配电箱,结合回路划分策略, 此类粒子编码能符合灯具回路的设计要求。
2.3.2 适应度函数
建立三维建筑电气布线设计模型的目标函数,如

式中的L 对应的是经济约束函数,W 对应的是安装约束函数,以上子目标函数的取值均越小越好;P 是物理约束函数,当回路尽可能少穿越墙体时,其值会越大,故此处取其倒数,100 为放大系数。 式中α,β,γ 为权重系数,取值范围均为[0,1]且之和为1,其取值大小决定了各自子目标在电气布局设计中的重要程度。 对于给定回路,各子目标之间往往是相互冲突的;因此需要平衡考虑路径对各子目标的满足情况,故本文采用加权求和法将多目标优化问题转化为单目标优化问题求解。
式(8)中,目标函数值越小表示电气布局设计效果越好,故将其转化为灯具回路以及插座回路的适应度函数,其中α,β,γ 依各自回路权重设置,如
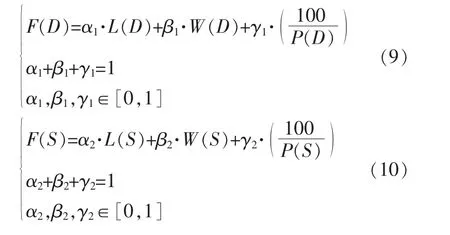
2.3.3 交叉操作
个体通过个体极值和群体极值交叉来更新,交叉方法采用整数交叉法。
1) 选择两个交叉位置,然后通过个体和个体极值或群体极值进行交叉, 若个体编码为[1,2,3,4,5,6,7,8], 极值为[6,8,2,4,5,7,1,2],随机选定交叉的位置为2 和4,则操作方法如下

2) 产生的新个体如果存在重复位置则进行调整,调整方法为用个体中未包括的灯具或插座代替重复的灯具或插座,如下所示

3) 对得到的新个体采用了保留优秀个体策略,只有当新粒子适应度值好于旧粒子时才更新粒子。
2.3.4 变异操作
变异方法采用个体内两位互换方法,首先随机选择变异位置1 及位置2, 然后把两个变异位置互换,若选择的变异位置为2 和4,则操作方法如下

对得到的新个体采用了保留优秀个体策略,只有当新粒子适应度值好于旧粒子时才更新粒子。
2.3.5 逆转操作
为避免陷入局部最优解,在变异操作后进行逆转操作, 对个体内随机产生的区间进行逆向换位,若选择的变异位置为2 和5,则操作方法如下

对得到的新个体采用了保留优秀个体策略,只有当新粒子适应度值好于旧粒子时才更新粒子。
3 仿真实验
3.1 算例描述
为检验上述模型及算法的效果,本文采用了一个包含办公室、会议室、大厅、走道、厕所5 个房间类型及1 个楼层配电间的办公建筑信息模型。 在模型中,房间灯具已按照实际设计要求布置好灯具及插座。
1) 需要对楼层电气设备进行回路划分,由房间属性可知,该层有5 个类型,按照回路划分策略,将其房间划分出8 条灯具回路及8 条插座回路,各房间所属回路结果如表1 所示。
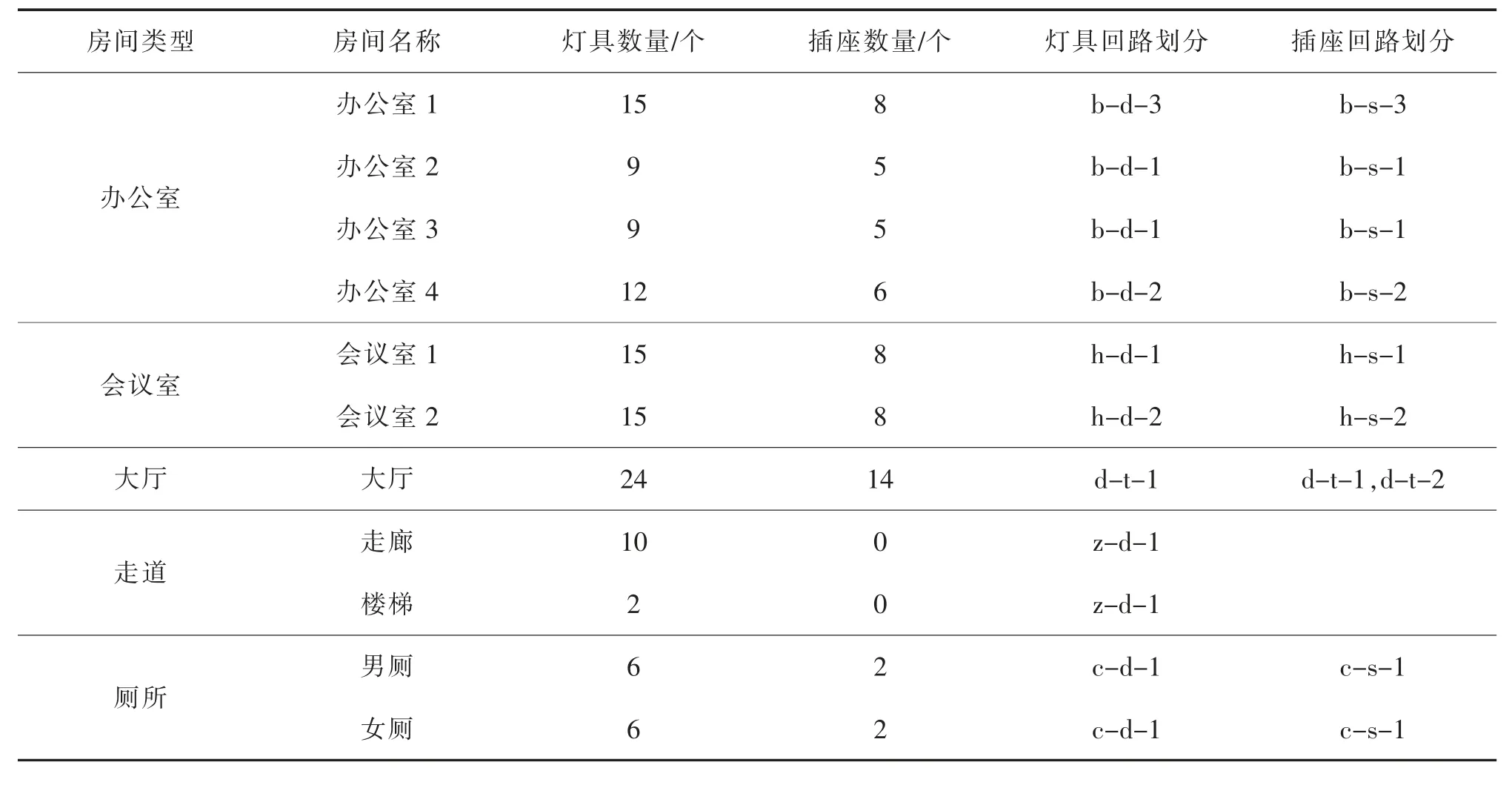
表1 楼层回路划分表Tab.1 Floor loop division
2) 回路划分后对上述房间和电气设备进行编号,方便实验结果查看,以办公室1 房间为例,其房间内的灯具编号为b-1-d-1~b-1-d-15, 插座编号为b-1-s-1~b-1-s-8, 回路划分后可确定粒子初始化维度。
3.2 参数设置
将三维建筑模型中左下角顶点视为空间原点,同时依次读取各电气设备空间坐标对应编号生成数据表格,根据数据表格确定各回路的粒子初始化维数,如灯具回路b-d-3,对应混合粒子群算法初始粒子维数设定为15。
本文算法参数设置如下:进化次数为200,种群规模为100;因灯具回路布置较为密集,弯头约束需占比较大,故回路权重系数α1,β1,γ1分别设置为0.4,0.1,0.5,插座权重系数α2,β2,γ2设置为0.3,0.2,0.5。弯头角度θ1的取值一般为2π/3,但在回路中,当偏转角度θ<π/3 时,按照弯头判定式(4),弯头数均为1,比较各自最优路径连接,适应度函数却在减小,为避免路径内产生交叉,需对此类连接状态进行惩罚,提高其适应度函数;当偏转角度θ=π 时,按照弯头判定式(4),弯头数为0,但此时为最优连接路径,此时需对此类连接状态进行奖励,应减小其适应度函数,故对安装约束中的弯头函数进行改进,提出线性偏转角度函数式(11)取代式(4)。

式中:λ 为奖惩因子,一般取值为1;以θ=π/2 为基准,此时弯头数为1,当θ=π 时,弯头数取值为-1。
3.3 实验结果及分析
为检验模型及算法的可行性,以办公室房间类型中的房间为例,同时引入董宗然[15]的普通遗传算法(GA)和原弯头函数(OWF)两组为对照组,改进的弯头函数组(LWF)为标准组,统一设置参数后,绘制三组的适应度函数随代数增加的收敛曲线如图1。 图1(a),图1(b)分别为办公室1 房间的b-d-3 灯具回路收敛曲线及b-s-3 插座回路收敛曲线。表2 为3 组算法在办公室房间类型内的回路统计结果。
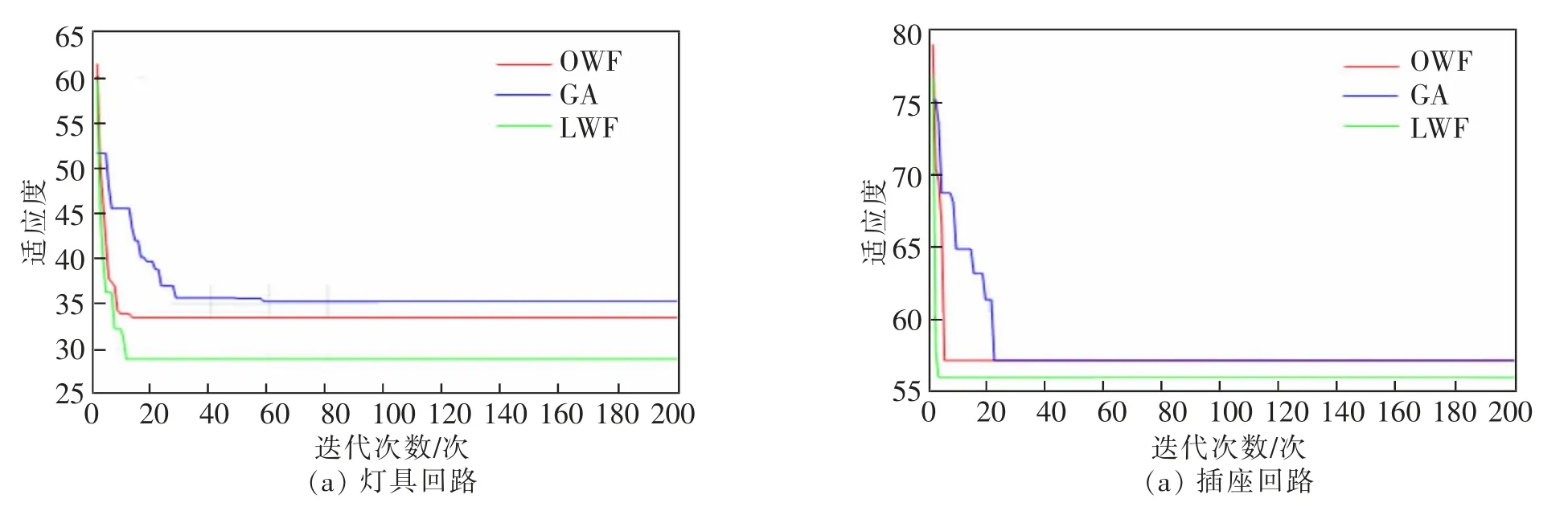
图1 3 组算法在灯具及插座回路的收敛曲线Fig.1 Convergence curves of lamps and sockets loops for three groups of algorithms
由图1 对比可知,3 组中GA 组较其他两组在最优适应度上过早陷入局部最优解,且无法跳出局部最优,LWF 组的收敛速度比较其他两组有明显的优势,且能以较少的代数找到次优解。 结合图2,针对不同回路,3 组都能以较快速度收敛到最优适应度值,三者在插座回路上均能找到最优设计回路; 在灯具回路中,LWF 组相对其他两组能有符合要求的设计回路,线路存在最少弯折点;OWF 组和GA 组的对比可知, 混合粒子群算法在收敛性及速度上更有优势, 能在前20 代就收敛到最优值,同时3 组在布局中均未出现路径交叉、重叠的现象发生,验证了该模型的可行性及准确性。

图2 楼层电气回路布线图Fig.2 Electrical circuit wiring diagram for each floor
表2 中列举了办公室类型房间的路径统计结果,实验将3 组算法在不同数量灯具及插座回路中去对比验证,记录其收敛最优值、弯头数和实际回路的线路长度。 因LWF 组采用改进的弯头函数,故会存在弯头数为负和零的情况;由表1 可知,按照楼层回路划分策略,b-d-1 回路实际包含两个房间的灯具,b-s-1 回路包含两个房间的插座,表2 中,3组算法均能在插座回路中找到同一组最优适应度值, 而在灯具回路上有不同的结果,LWF 组的结果在实际路径略差一些,但在弯头数量上优于其他两组; 表中其他回路结果也都表明,LWF 组在灯具回路和插座回路设计布局中优于其他两组,混合粒子群算法优于普通遗传算法,该数学模型在灯具和插座设计回路上均能较满足回路设计的要求,具有一定的可行性。

表2 布线路径统计结果Tab.2 Statistical results of wiring paths
按照LWF 组的参数设置, 将该楼层的其他房间回路设计结果布局到实际三维建筑模型中,结果如图2 所示, 虽然LWF 组能实现较为符合要求的设计回路,但其还存在实际线路长度无法稳定收敛到最优值及模型中的回路权重参数、弯头函数的奖惩因子设置需要依靠经验设置的问题。
4 结论
1) 提出了一种基于混合粒子群的三维建筑电气布线设计方案, 通过分析建立了一种符合办公建筑内的数学模型, 该模型综合考虑了多种电气设计约束,选择线缆长度来表示经济约束、设立弯头函数计算弯头数表示安装约束, 在解决物理约束中的回路设备数量问题时,引入回路能量法。 同时依靠提出的基于房间属性的回路划分策略,确定了各回路上的电气设备数量, 能合理划分楼层电气设备回路。
2) 在验证模型及算法的可行性时,设置了普通遗传算法组为对照组,结果表明混合粒子群算法在收敛速度已经寻优能力上有提升;为减少回路中的弯头数和避免出现回路交叉现象,对弯头函数进行了改进,对比实验表明改进的弯头函数对算法结果有明显提升,在回路布局的求解质量和效率上具有可行性和先进性。

