基于ICEEMDAN的矿井供电系统故障测距方法

谢子殿， 范树凯

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

我国煤矿井下的供电系统通常采用中性点非有效接地系统。井下条件复杂，线路易发生单相接地故障，若故障不及时排查定位，容易发生输电线路的击穿，严重威胁工作人员的人身安全和用电设备的安全有效运行，因此,有必要及时对故障位置进行精确定位,预防可能存在的危险。

近年来，国内外的专家学者针对故障测距提出了诸多方法，其中主要分为阻抗法、信号注入法、行波法和人工智能法。阻抗法[1]运算简单经济，但过渡电阻会影响阻抗法的测量精度。信号注入法[2]只需单个脉冲发射装置，但接地电阻会影响信号注入法的测量精度。人工智能法[3]抗扰动能力强，但需要大量的数据样本且普适性差。综合分析，目前行波法是实现故障测距较为有效的方法。在行波测距的方法中小波模极大值法[4]和希尔伯特黄变换[5]等行波波头提取方法，小波分析法具有较好的时频特性，但基函数的选取和分解尺度的选择问题会造成测距偏差；希尔伯特黄变换有较好的自适应特性，但在分解过程中无法有效抑制模态混叠现象，出现丢失故障信息。为了解决煤矿井下条件复杂，噪声掩盖有效的故障稳态信号影响故障定位等问题，笔者提出一种煤矿井下的电缆测距新方法，利用一种可以表示所有故障情况线模分量的模态变换对故障波形进行解耦，通过形态学去除模拟的煤矿井下干扰噪声、利用改进的自适应噪声的完全集合经验模态分解(ICEEMDAN)具有良好的时频特性的特点，将电压线模分量分解成不同的特征频带，运用 Teager 能量算子对合适的频带进行信号的跟踪，仿真验证故障测距算法的有效性。

1 新相模变换矩阵与形态学去噪

1.1 新相模变换矩阵

行波测距前，为了消除线缆间发生的耦合现象，采用相模变换的方法进行解耦。目前，Clarke、Karenbauer等常用的相模变换矩阵广泛应用于继电保护等领域，但这些变换阵的缺点是在故障测距暂态分析中无法反应所有的故障类型。在文献[6]中，提出了一种新的相模变换矩阵，该变换矩阵既有时域变换矩阵的特性，又完成了对单相接地、多相接地等各种故障类型的单一模量分析。其矩阵的原始矩阵为

(1)

经过施密特单位化和正交化变化为

(2)

1.2 形态学去噪

考虑到在煤矿井下电压电流传输的过程中可能会受到噪声干扰信号的影响，通过添加高斯白噪声模拟井下条件的传输波形发生畸变，为了防止噪声掩盖有效故障的信息，首先，通过形态学滤波来预处理故障行波。形态学滤波是利用形态学运算对各种形态信息的构成元素分析，完成噪声的抑制。形态学滤波器使用提前规定好的结构信息在行波信号的几何特点基础上，对信号进行采样对比，达到去除多余的噪声，保留好信号特点的同时还原信号本身。

根据文献[7]中表示结构元素，采用盘型结构元素，这种结构元素构成简单，计算量小，同时在抑制噪声和保留信号特征方面效果较好。使用一种经过高帽滤波和低帽滤波的噪声基线校正算法，同时，将基线校正获得的信号放入到噪声抑制算法中，在不牺牲信号质量的同时去除噪声，噪声抑制算法如图1所示。

图1 噪声抑制算法Fig. 1 Noise suppression algorithm

2 ICEEMDAN与TEO算法

2.1 ICEEMDAN原理与算法

改进的自适应噪声的完全集合经验模态分解是Marcelo等[8]提出的信号处理方法。因为在分解带有噪声影响的信号时，使用 EEMD会产生数量不一致的 IMF，从而影响分解的低频高频的准确度，相对而言 CEEMDAN 抗噪性能好，鲁棒性强，可以有效解决外加噪声信号的问题，提出了新的方法 ICEEMDAN，与CEEMDAN不同的是在加入用于信号处理的噪声方面，不是采用一般的高斯白噪声，而是加入了一种特殊的噪声分解信号。具体而言，ICEEMDAN 在分解层中分解为多个IMF和与其对应的残差信号，IMF获取是特有的残差信号和其截取的部分均值的相差大小。特有残差的获取是通过EMD分解高斯白噪声得到的第k层IMF获取的。通过测试的实验数据显示，因为 EEMD 产生 IMF 数量不一致出现的平均值相关情况，剩余部分噪声的未被消除的问题得到了进一步解决，计算步骤分4步。

步骤1向初始信号加 EMD 分解得到特殊的噪声

x(i)=x+β0E1[w(i)]，

(3)

式中：x——初始信号；

E1[w(i)]——特殊噪声；

w(i)——添加信号中的第i个白噪声。

步骤2求取改造后信号的局部平均值是用EMD算法，取它们平均值得到第一个残差，计算IMF值

(4)

(5)

式中：r1——一阶残差；

步骤3计算第2个IMF值为

(6)

(7)

式中：r2——二阶残差；

步骤4依照以上步骤的计算继续使用公式， 求出第k个 IMF 值。

(8)

(9)

式中：rk——k阶残差；

通过迭代计算，惩罚可以准确地分解出IMF分量。

2.2 Teager 能量算子

Teager 能量算子[9]是一种可以迅速反映信号变化、运算方面快速的非线性能量算子。根据其特性，多用于行波信号暂态的检测，因此，在故障行波检测的波头提取上，运用TEO完成最后的故障行波到达测试点的时间为

ψ[s(t)]=s2(t)-s(t)s″(t)，

(10)

式中：s(t)——故障信号；

ψ——能量算子；

s′(t)——s(t)的导数。

在离散信号的处理上，可以表达为

ψ[s(n)]=s2(n)-s(n+1)s(n-1)。

(11)

3 测距算法与流程

3.1 双端测距算法

在双端行波测距算法通常用到故障点产生的行波速度和行波到两个检测点的相差时间定位，文中采用文献[10]中新的双端行波测距方法，利用故障发生时间与波头到达两检测端检测点的差值测距。此方法与需要计算行波波速的方法相比故障定位更加可靠，精度更高。

3.2 测距流程

煤矿井下供电系统发生线缆故障时，测距步骤如图2所示。

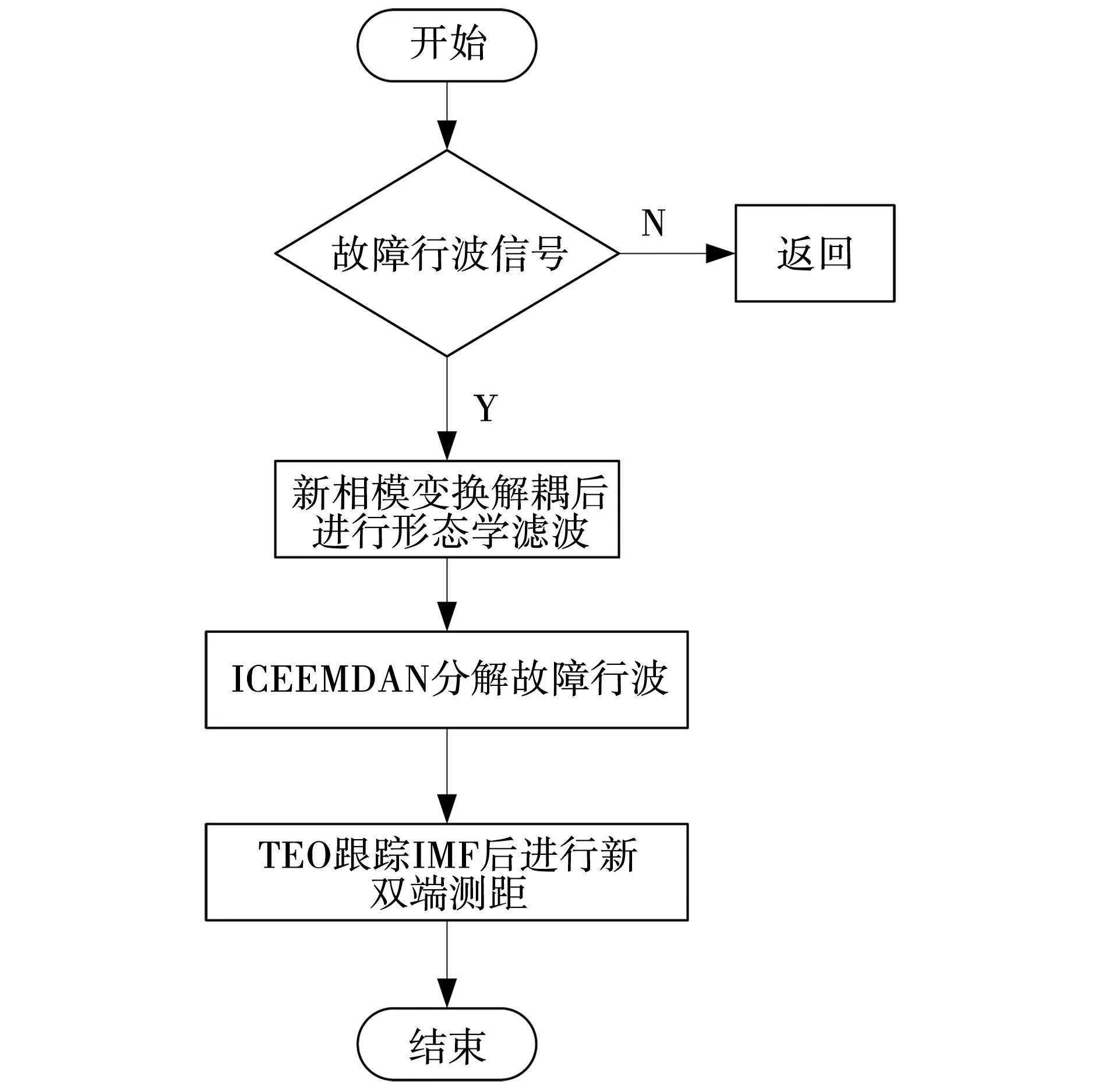
图2 测距流程Fig. 2 Ranging flow

步骤1矿井供电安全监测系统检测到故障电流突变时进行检测，读取故障行波信号。

步骤2采用新型相模变换方法进行解耦，防止故障类型对测距影响的判断。

步骤3运用形态学滤波去除煤矿井下噪声故障行波的影响。

步骤4将滤波后的故障行波信号进行ICEEMDAN分解，在进一步去噪处理的同时，处理得到不同频带的IMF分量。

步骤5通过Teager能量算子跟踪IMF分量，得到故障行波到达检测点的时间，使用一种不受行波速度影响的双端测距方法，计算出故障发生点。

4 仿真验证与分析

4.1 仿真模型的搭建

采用Matlab/Simulink仿真平台搭建了矿井10 kV辐射型输电系统，一共有4条馈线L1、L2、L3和L4，线路长度在7～30 km不等，且经消弧线圈接地，配电网的线缆故障仿真模型如图3所示。其中，线缆参数如表1所示。

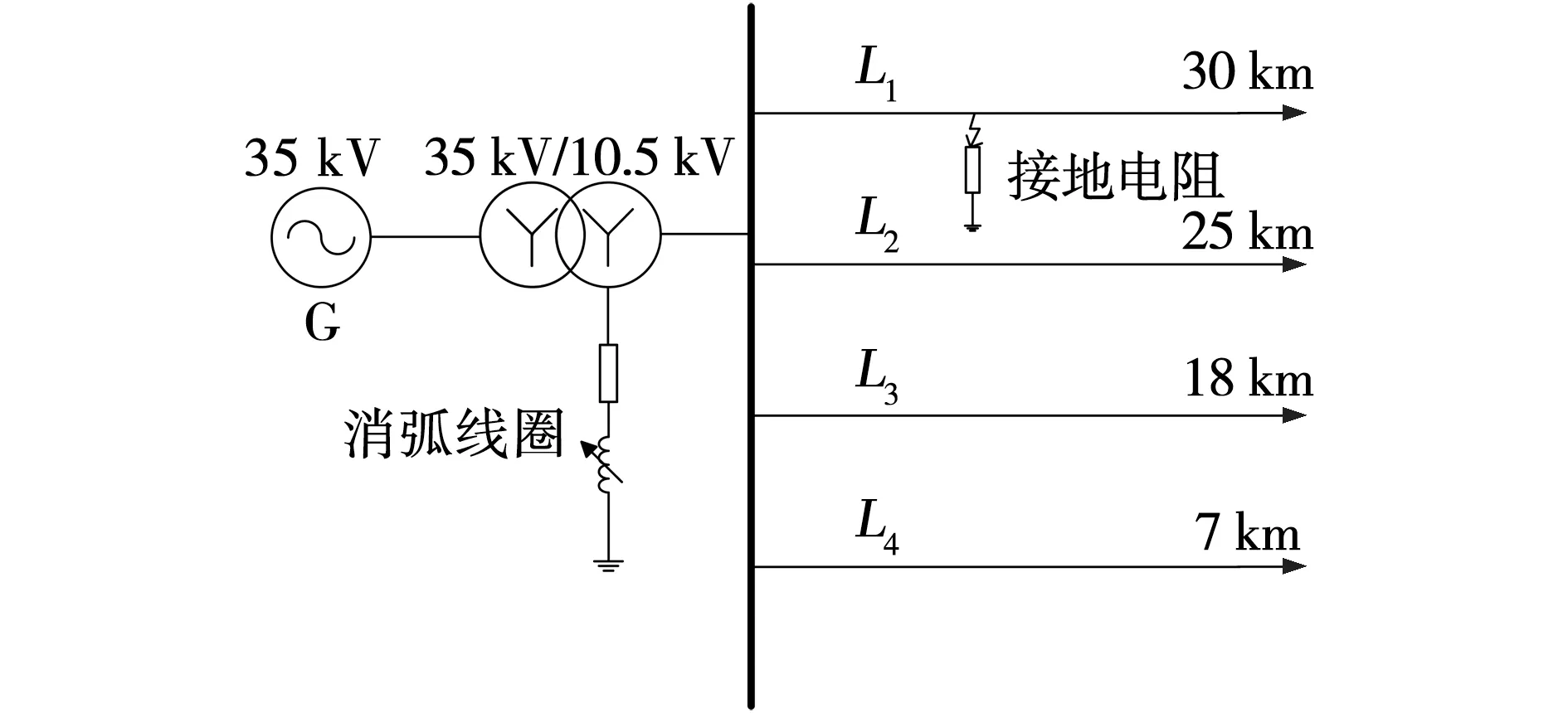
图3 测距故障仿真模型Fig. 3 Fault location simulation model

表1 线路模型参数

在仿真中采样频率为1 MHz，设定馈线L1在t=0.035 s时,距离母线处检测点10 km发生单相接地故障。加入符合矿井噪声特点的高斯白噪声进行模拟，消弧线圈的过补偿额度设定为10%，接地电阻取值为100 Ω,截取发生故障后的4 ms进行仿真分析，如图4所示。

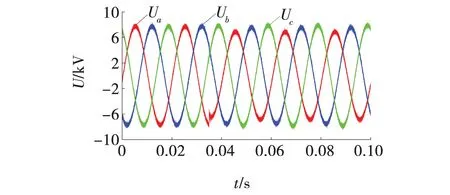
图4 线路L1首端M的三相电压波形 Fig. 4 Three phase voltage waveform of line L1head end M

4.2 测距过程

在对电流行波进行新相模变换后得到故障电压信号的正序分量，然后利用形态学滤波对馈线L1的故障波形进行初步噪声去除，截取故障前后1 ms的故障波形及滤波波形如图5所示。

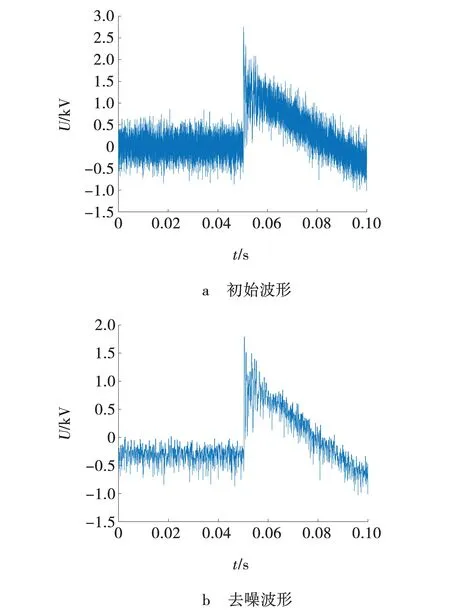
图5 正序分量初始波形及去噪波形Fig. 5 Initial waveform and denoising waveform of positive sequence component

利用ICEEMDAN算法分解滤波波形，得到从频率高到低排列的IMF分量，然后提取出最高频的IMF分量即IMF1进行下一步分析，IMF1分量瞬时幅值波形如图6所示。

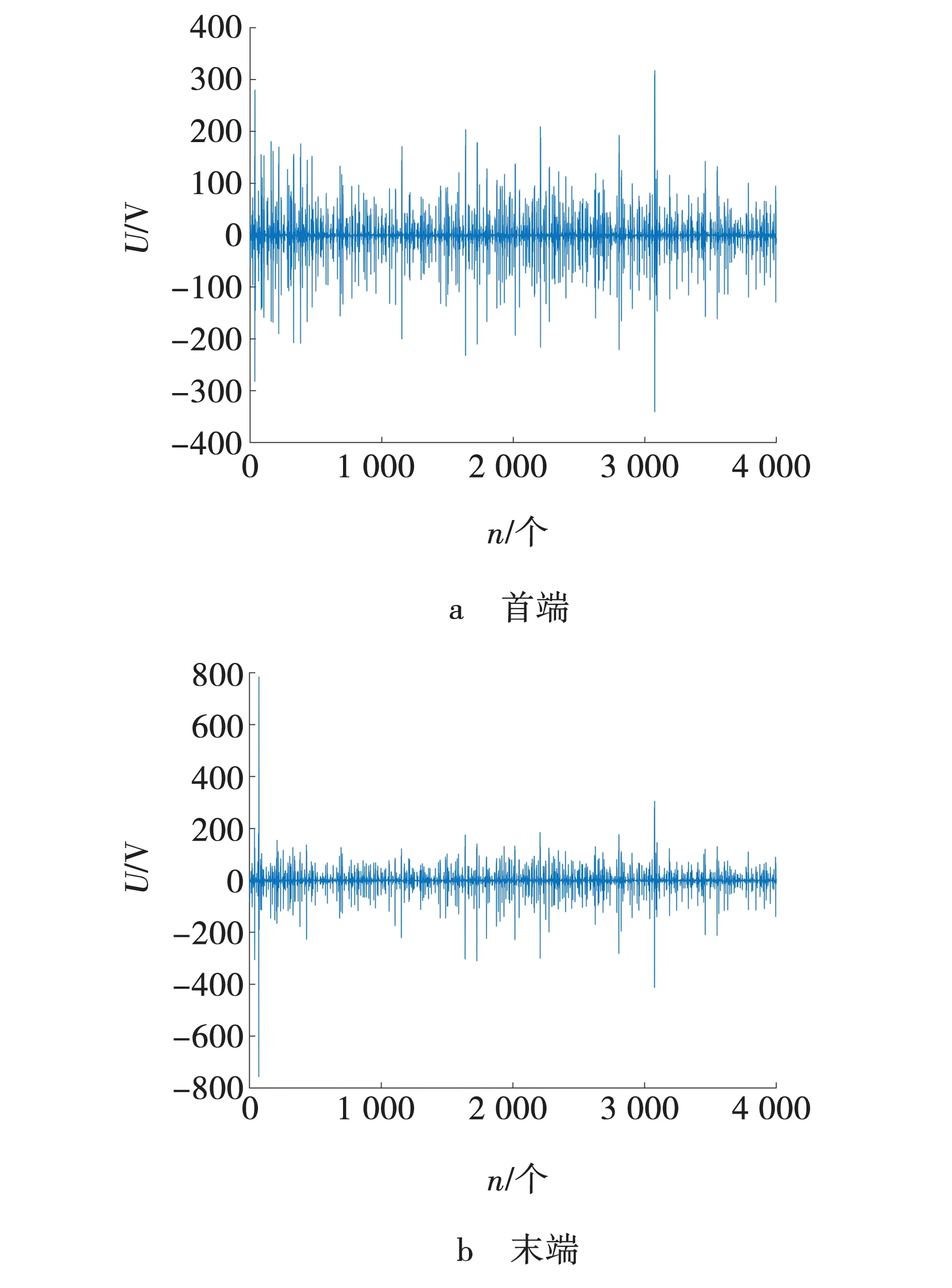
图6 首端M及末端N电压的IMF1分量 Fig. 6 IMF1 of head end M voltage and terminal N voltage

通过Teage能量算子计算筛选出的模态IMF，馈线L1末端故障电流的正序分量经过ICEEMDAN分解的高频,得到初始故障行波到达检测点的时刻。模态的瞬时能量谱如图7所示。由图7可知，线路首段初始故障信号在t0=34 μs时到达检测点首端M，在t1=69 μs时到达线路故障末端N。

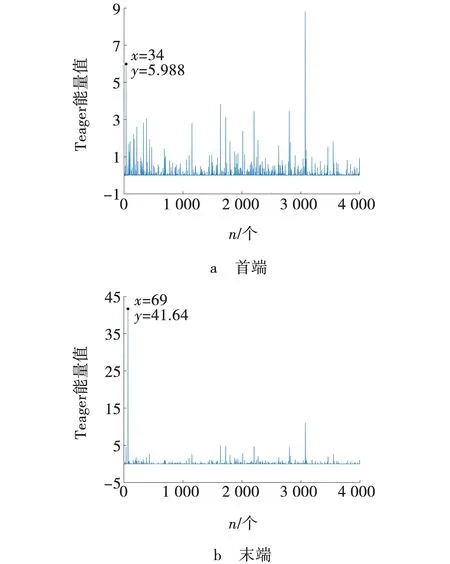
图7 双端IMF1瞬时能量谱Fig. 7 Double terminal IMF1 instantaneous energy spectrum

已知给定路线长度为30 km，初始故障行波波头到达M、N两端的时间分别为t0=34 μs和t1=69 μs，利用不受波速影响的双端测距算法计算得到故障发生距离为9.902 9 km，与设定故障距离10 km相比较，误差为0.097 1 km，相对误差为0.32 %，测距误差较小，精确度较高，可以完成有效测距。同样解耦故障行波后，使用EMD变换算法检测HHT算法故障行波，初始故障行波到达检测点的结果如图8所示。

由图8可知，由于EMD含故障有效信息的高频分量被噪声淹没，在HHT频谱图中难以寻找初始故障行波波头到达检测点的精确时间，无法完成精确测距。经过上面的波形处理方法对比得出使用形态学滤波、ICEEMDAN算法和TEO算法结合的测距方法有效性和适应性更好。

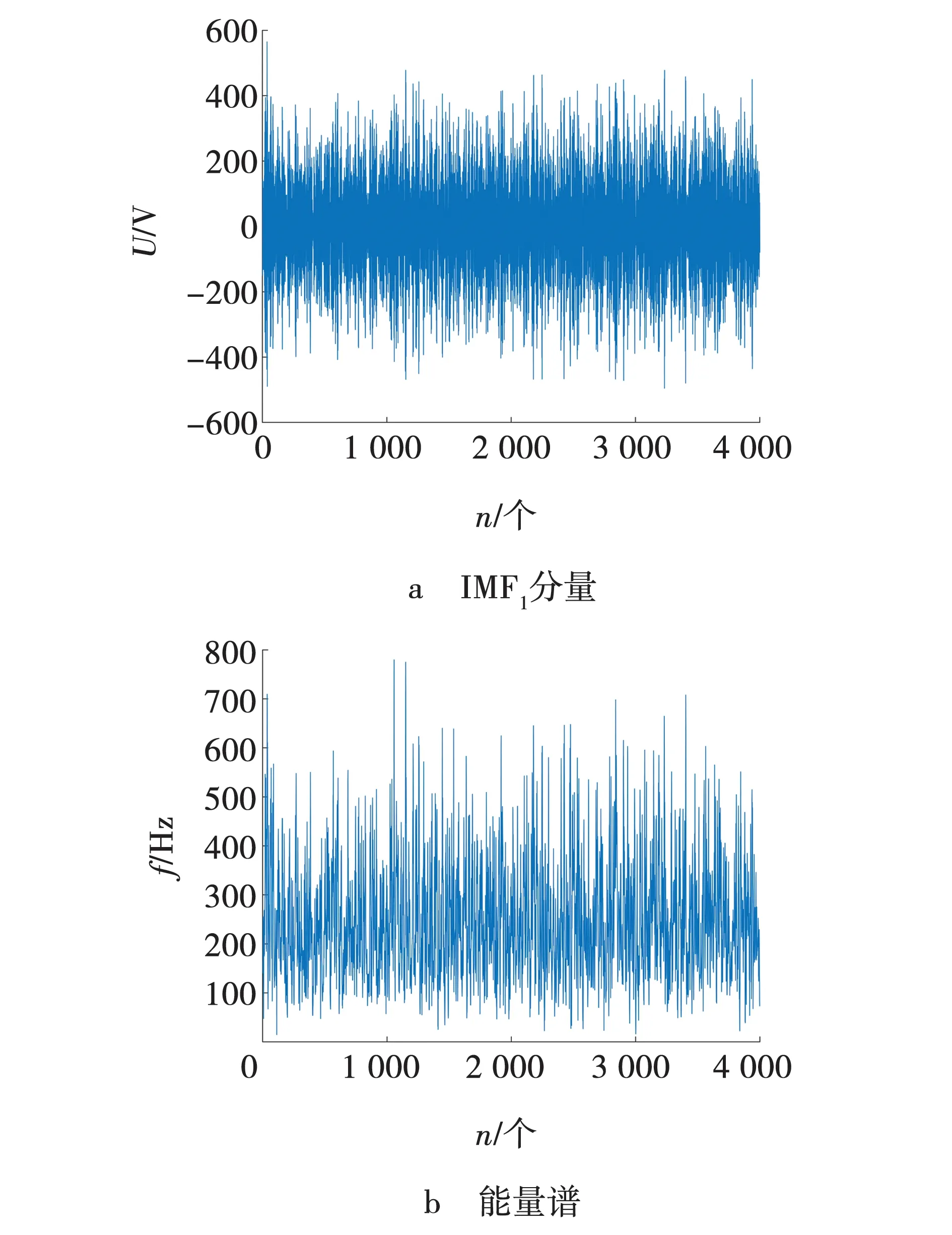
图8 EMD的IMF1分量及HHT瞬时能量谱Fig. 8 IMF1 component and HHT instantaneous energy spectrum

4.3 不同故障参数对测距精度的影响

以Matlab/Simulink矿井配电网接地故障仿真分析，影响因素有过渡电阻、故障点位置、接地故障类型等不同故障参数的影响，下面讨论这些影响因素对最终测距结果造成的影响。不同故障距离lg下，线路发生故障时测距得到的计算距离ls和相对误差e大小如表2所示。

表2 不同故障距离下测距精度

由表2可知，线缆在不同故障距离下，算法的最终测距结果精确度都较高。暂态零序电流高频分量的大小在某种程度上会受到过渡电阻Rg大小的影响。仿真电缆设置故障距离为10 km，验证了不同过渡电阻对测距算法的影响，如表3所示。

表3 不同过渡电阻下的测距精度

根据结果可以得到该算法不会受到过渡电阻大小的影响。仿真电缆设置故障距离为10 km，发生不同故障类型时，故障的测距结果见表4。

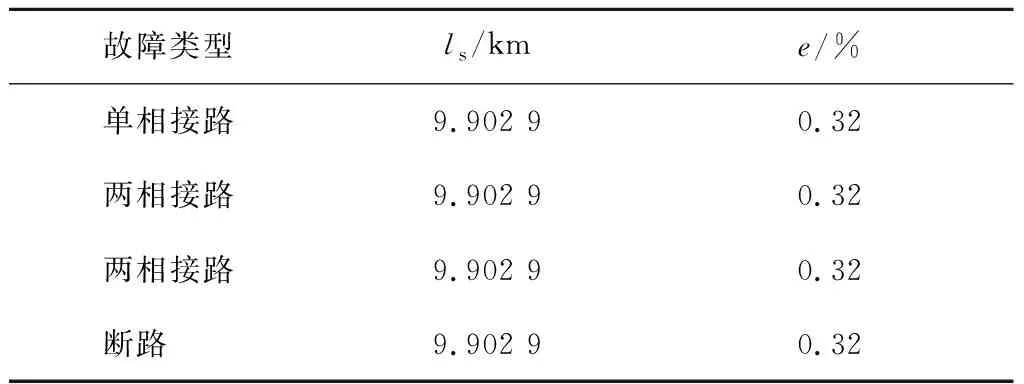
表4 不同故障类型下的测距精度

由表4可知，该算法其它影响参数相同的条件下，不受单相接地、多相接地线路断裂等多种故障类型测距类型的影响，具有广泛的适用性。

5 结 论

(1)针对10 kV经消弧线圈接地的矿井配电网,提出了一种基于新相模变换、形态学滤波、ICEEMDAN和Teager能量算子的在线故障测距方法。配电网发生接地故障时，通过滤除杂波影响，提取故障行波高频低频部分，选择合适的IMF进行能量算子跟踪，双端测距完成工作。

(2)与传统的EMD方法对比，此测距方法能较好地处理有噪声影响的故障行波信号，同时验证了该测距方法在不同过渡电阻、不同故障距离和不同故障类型下多种故障参数的测距精确度，实验结果表明，在单相接地故障和10 dB高斯白噪声干扰的条件下，测距相对误差为0.32%。