碟盘振动截割煤岩的参数优化与性能评价

刘春生， 车长瑞， 刘延婷， 程 硕

(1.黑龙江科技大学 机械工程学院， 哈尔滨 150022； 2.黑龙江科技大学 安全工程学院， 哈尔滨 150022)

0 引 言

机械法破碎煤岩性能的研究一直是煤矿机械研究的重点。杨迎新等[1]实验研究单齿垂直压入岩石性能，定量评价不同齿形对不同性质岩石的破岩效率。闫铁等[2]建立了岩石破碎比功的模型，提出一种基于破碎比功评价破岩效率的模型。李玮等[3]通过建立岩石破碎能耗的分形模型，评价了实钻条件下的钻头破碎能耗。赵贺兴等[4]分析破岩比能与刀间距和磨损量之间的关系，为刀具更换提供理论依据。邓嵘等[5]采用模糊综合评判方法将牙齿破岩体积、破岩面积、齿坑深度及牙齿最大应力结合,选出破岩效率较高的齿形。胡琴等[6]采用模糊正交法优选了多组齿形参数，提高了钻头破岩效率。刘春生等[7]通过正交数值模拟实验，采用功效系数法评价碟盘刀具破碎性能。翟强等[8]采用改进群层次分析法和指标相关性法评价TBM滚刀破岩性能。段志伟[9]基于多元线性回归关系和神经网络得到准确性较好的TBM围岩分级贯入度预测模型。李雷等[10]以DYNAFORM数值模拟、人工神经网络和NSGA-Ⅱ多目标遗传算法为研究手段，对封头成形工艺参数进行多目标优化。基于上述研究成果，笔者采用ABAQUS软件对碟盘振动截割煤岩进行数值模拟，依据碟盘齿数、煤岩强度、进给速度、振动频率、振动幅值设计18组正交数值模拟，运用变异系数法和TOPSIS法对多指标综合评价，18组数值模拟载荷峰值均值进行多元回归拟合，采用极差法分析各参数对碟盘振动截割煤岩性能的影响程度，通过多目标遗传算法进行参数优化，为确定各参数对碟盘振动截割煤岩的性能影响、合理确定参数具有一定的参考。

1 数值模拟设计

1.1 正交数值模拟

为评价碟盘振动截割煤岩性能，应用ABAQUS软件建立碟盘振动截割煤岩有限元模型，如图1所示。在切削厚度h=15 mm条件下，根据碟盘齿数、煤岩强度、进给速度、振动频率、振动幅值，设计5因素3水平共18组数值模拟。数值模拟因素水平设计如表1所示，18组数值模拟如表2所示。

图1 碟盘截割煤岩模型Fig. 1 Model of cutting coal and rock with dish

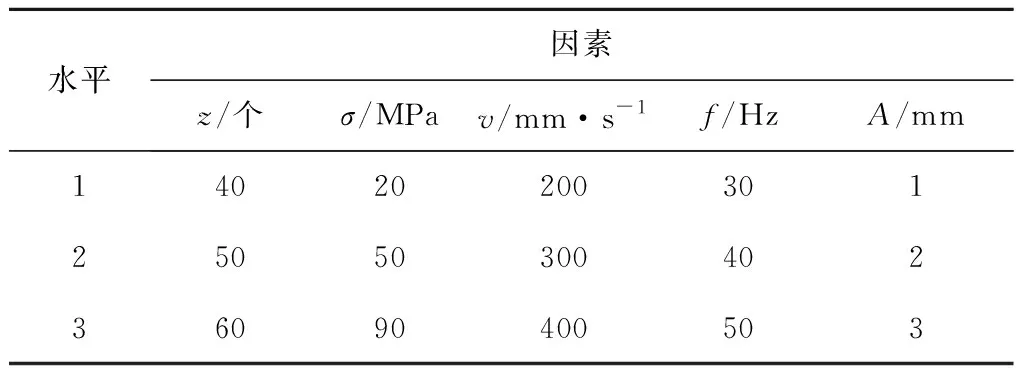
表1 正交数值模拟因素水平

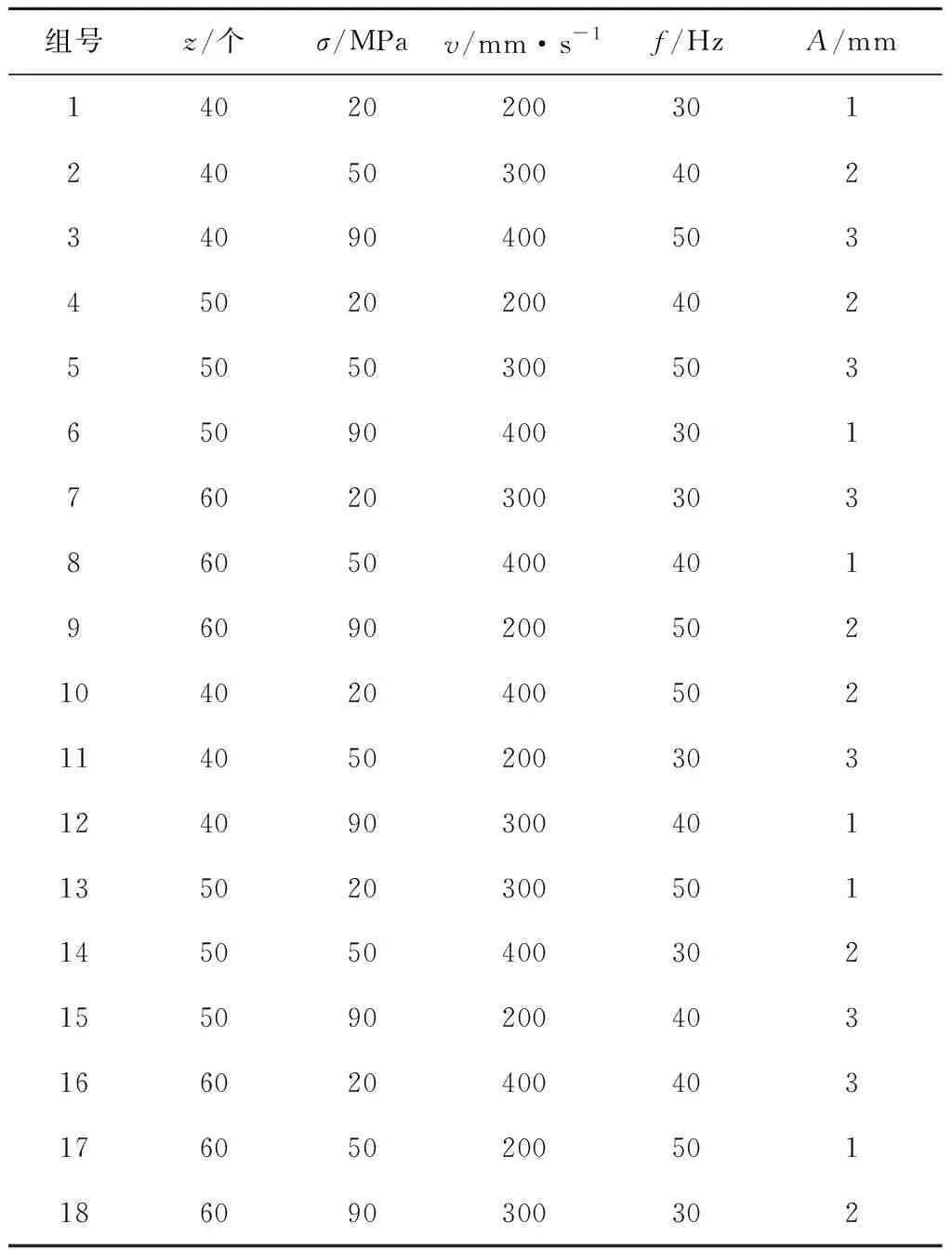
表2 18组正交数值模拟

1.2 数值模拟结果

根据数值模拟得到碟盘振动截割煤岩的18组载荷谱，选取3组不同工况下的径向载荷、轴向载荷曲线，如图2所示。通过18组载荷谱得到各工况下径向载荷峰值均值Fje、轴正向载荷峰值均值Fzz、轴负向载荷峰值均值Fzf，如表3所示。

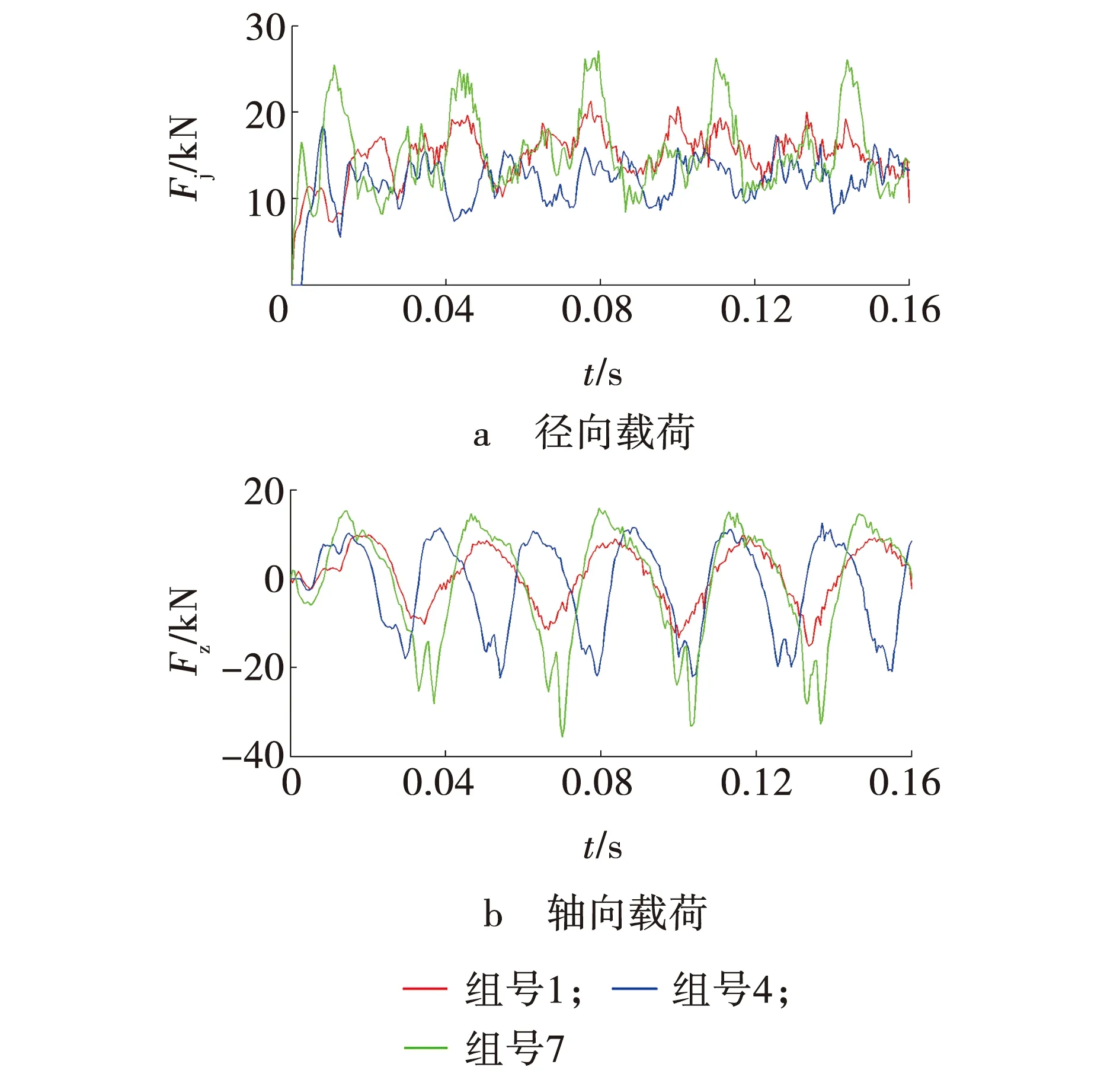
图2 数值模拟载荷曲线Fig. 2 Load curve of numerical simulation

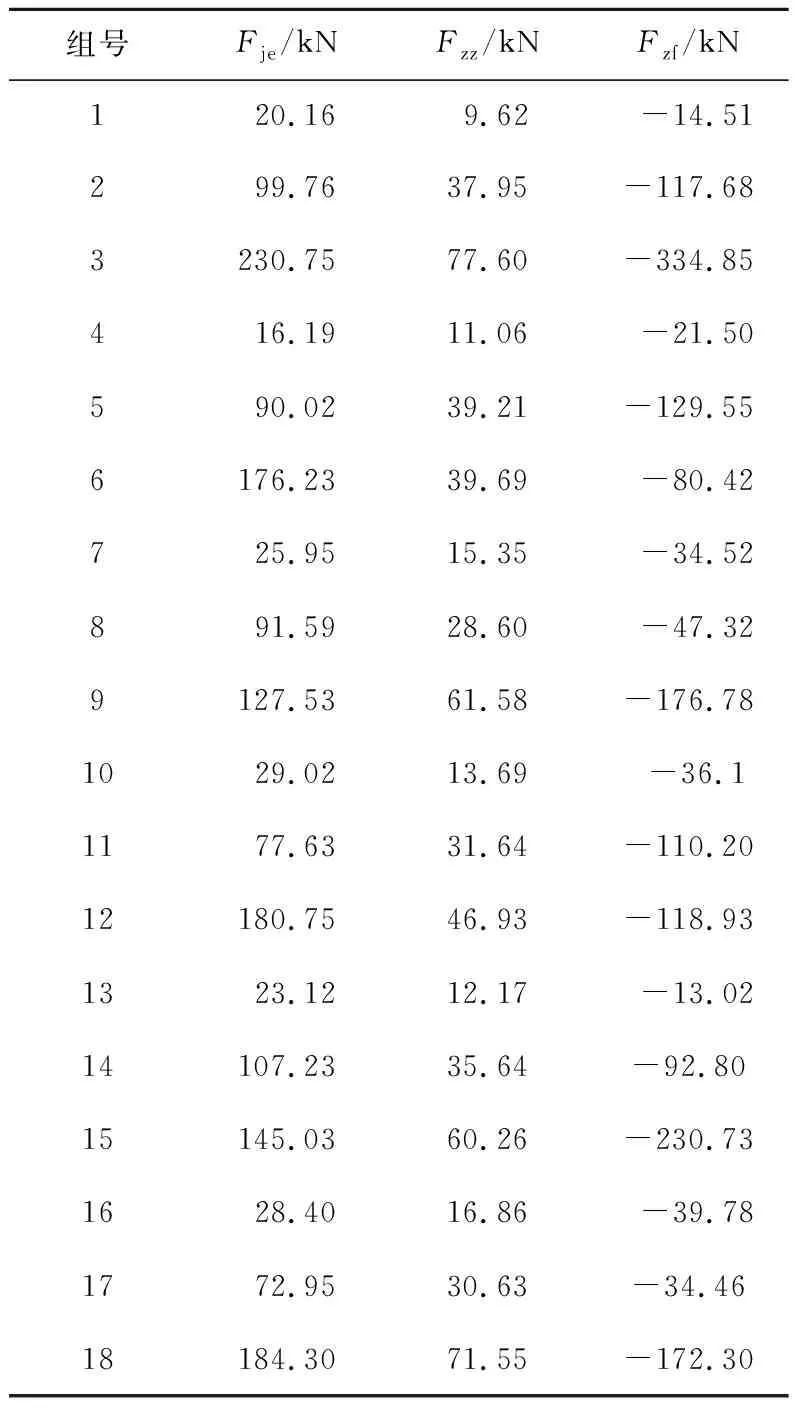
表3 18组数值模拟结果

2 性能综合评价模型

2.1 评价指标标准化归一化

设定数值模拟为i组，i=1，2，…，m，评价指标数为j个，j=1，2，…，n，组成i行j列的原始数据矩阵Xij为

由于评价指标的不同，对指标分别进行正向化和负向化处理[11]。正向指标标准化与负向指标标准化为

评价指标的数值与量纲有较大差别，在进行综合评价前需要对各项评价指标进行归一化处理，得到归一化后矩阵Yij为

2.2 变异系数法确定权重

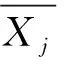
通过变异系数法确定的权重wj为

通过变异系数法对18组数值模拟的评价指标进行权重分配，其中径向载荷峰值均值权重为0.362，轴正向载荷峰值均值权重为0.369，轴负向载荷峰值均值权重为0.269。

2.3 TOPSIS综合评价

TOPSIS法根据有限个评价对象与理想化目标的接近程度进行排序，是在现有的对象中进行相对优劣的评价方法。基本思路是假定正、负理想解，测算各样本与正、负理想解的距离，得到其与理想方案的相对贴近度，进行各评价对象的优劣排序[13]。提取正理想解单元与负理想解为

正负理想解单元为

计算各样本距离正负理想解的距离，即欧几里德绝对距离为

计算各评价值的公式为

对归一化和权重分配后的矩阵进行TOPSIS法综合评价，得到18组数值模拟的综合评价值如表4所示。

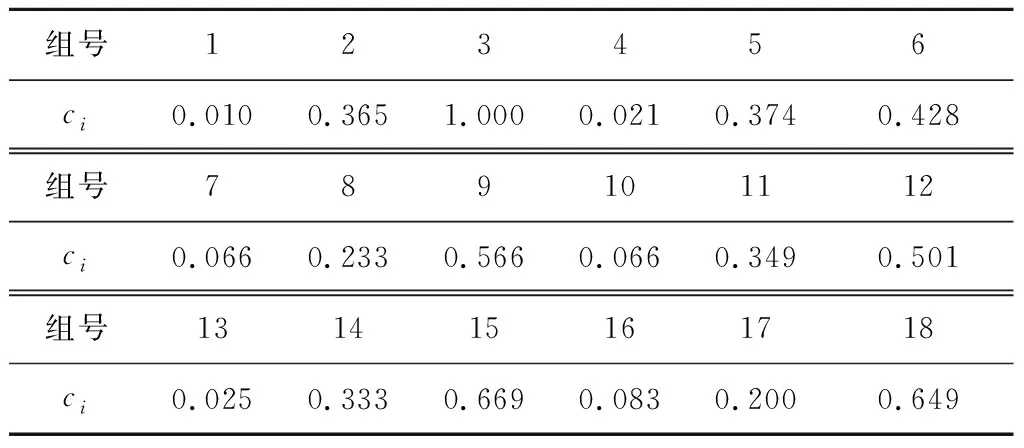
表4 TOPSIS综合评价值

根据径向载荷峰值均值、轴正向载荷峰值均值、轴负向载荷峰值均值的综合评价，综合评价值越小时，安全系数越高，综合评价最优。由表3、4可知，当σ=20 MPa时，第1组数值模拟的综合评价值最小；当σ=50 MPa时，第17组数值模拟的综合评价值最小；当σ=90 MPa时，第6组数值模拟的综合评价值最小。

3 极差分析与遗传算法参数优化

3.1 性能评价及参数优化

通过变异系数法与TOPSIS法对18组正交数值模拟进行综合评价后，采用极差法分析参数对碟盘振动截割煤岩的性能影响程度，通过数值模拟结果建立目标函数，运用多目标遗传算法优化，得到优化参数数值模拟结果与TOPSIS法排序最优组号的数值模拟结果进行对比分析，确定最优参数组合，其优化流程如图3所示。

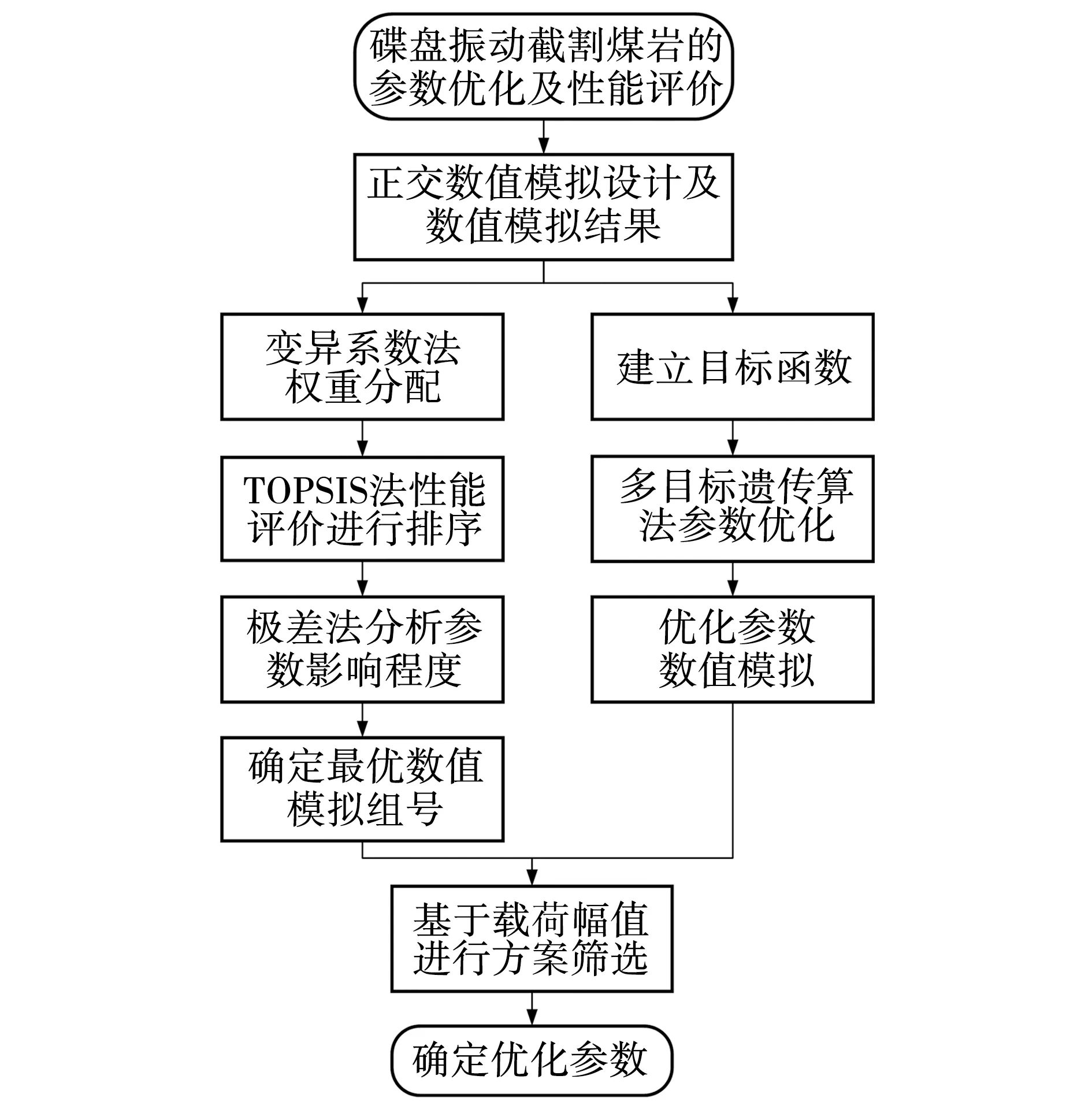
图3 性能评价及参数优化流程 Fig. 3 Flow of performance evaluation and parameter optimization

3.2 极差分析法

运用极差法分析表3、4数据的结果如表5所示，同一指标最大值与最小值差距越大表明影响程度越大，说明对碟盘振动截割煤岩的性能影响程度越大。

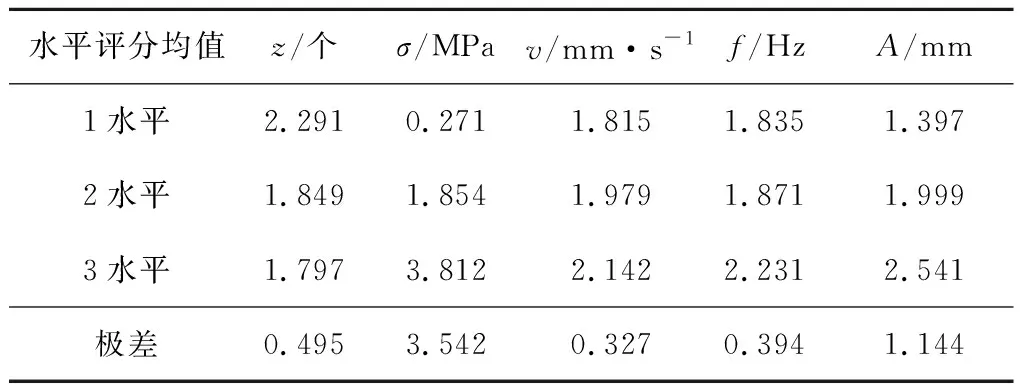
表5 极差分析结果

由表5可知，对碟盘截割煤岩性能影响程度由大到小依次为煤岩强度、振动幅值、碟盘齿数、振动频率、进给速度。

3.3 多元回归模型的建立

假设正交数值模拟实验中结果为因变量，参数为自变量，考虑因素间的相互作用，采用多元回归分析。建立径向载荷峰值均值Fje、轴正向载荷峰值均值Fzz、轴负向载荷峰值均值Fzf的回归模型，各项系数如表6所示。

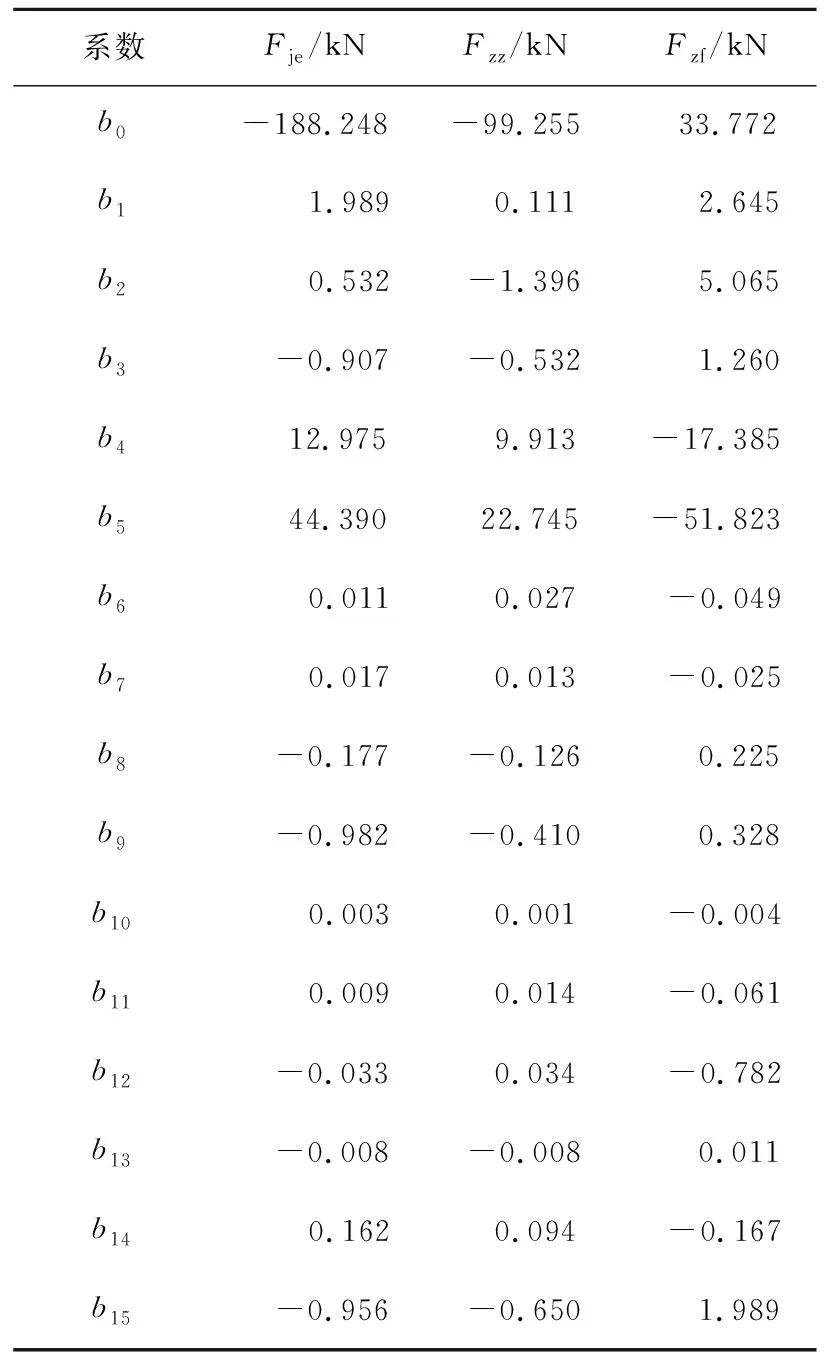
表6 多元回归模型系数

F=b0+b1x1+b2x2+…+bkxk+…+

bk+1x1x2+bk+2x1x3+…+bnxk-1xk。

3.4 多目标遗传算法参数优化

通过构建碟盘截割煤岩径向载荷峰值均值、轴正向载荷峰值均值、轴负向载荷峰值均值的目标函数进行多目标遗传算法的寻优计算，煤岩强度在20、50、90 MPa时优化的约束范围为40≤z≤60、200≤v≤400 mm/s、30≤f≤50 Hz、1≤A≤3 mm，进行xn次多目标遗传算法寻优。设置最优前端个体系数为0.002，种群大小为500，最大遗传代数为1 000，停止代数为1 000，适应度函数偏差为1×10-100，调用函数GA来运行，得到Pareto最优解，如表7所示。

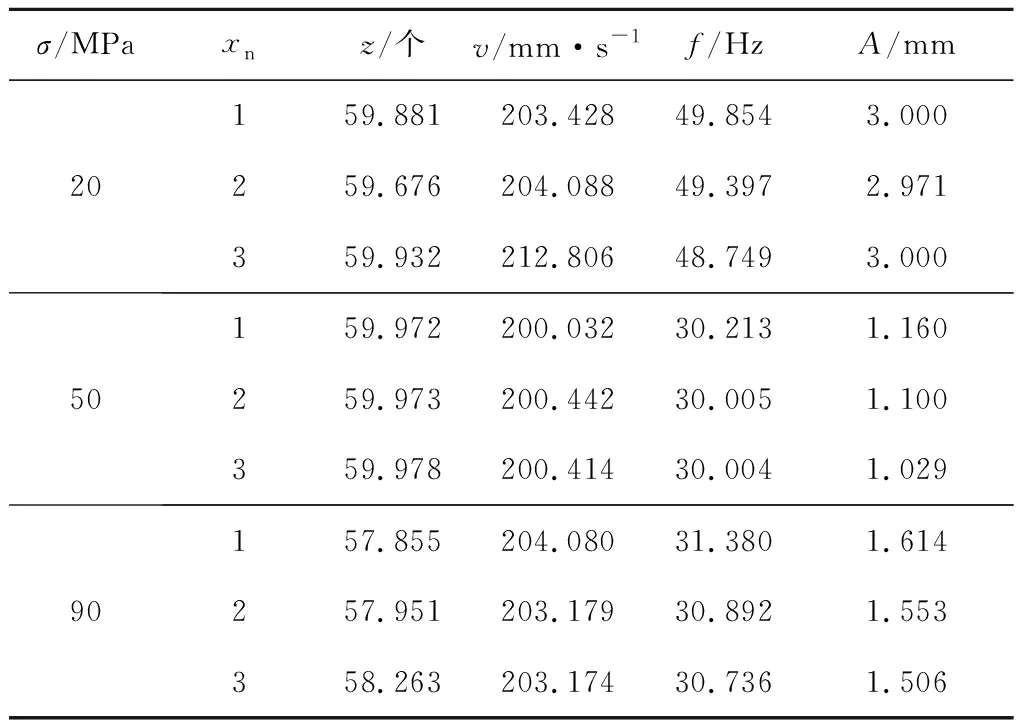
表7 多目标遗传算法优化

当σ=20 MPa时，多目标遗传算法优化参数为z=60，v=200 mm/s，f=50 Hz，A=3 mm；当σ=50 MPa时，多目标遗传算法优化参数为z=60，v=200 mm/s，f=30 Hz，A=1 mm；当σ=90 MPa时，多目标遗传算法优化参数为z=60，v=200 mm/s，f=30 Hz，A=1.5 mm。

3.5 参数优化对比

对多目标遗传算法优化的参数进行碟盘振动截割煤岩数值模拟，在煤岩强度为20、50、90 MPa时，将多目标遗传算法优化参数进行数值模拟，分别与综合评价值最优的第1、17、6组数值模拟进行对比，对比载荷曲线如图4所示，载荷峰值均值如表8所示。

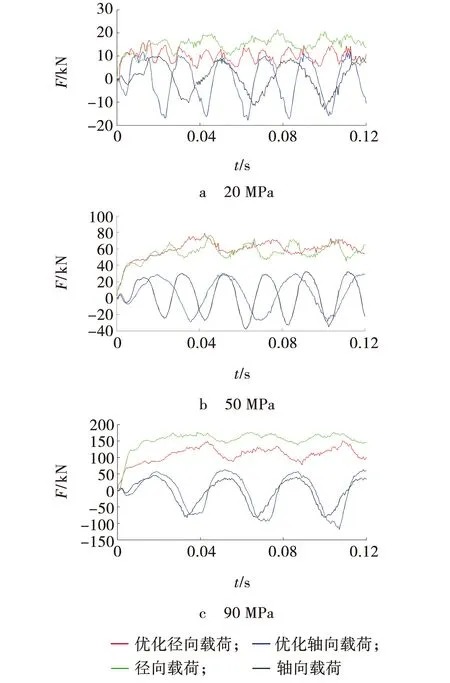
图4 载荷曲线对比Fig. 4 Load curve comparison

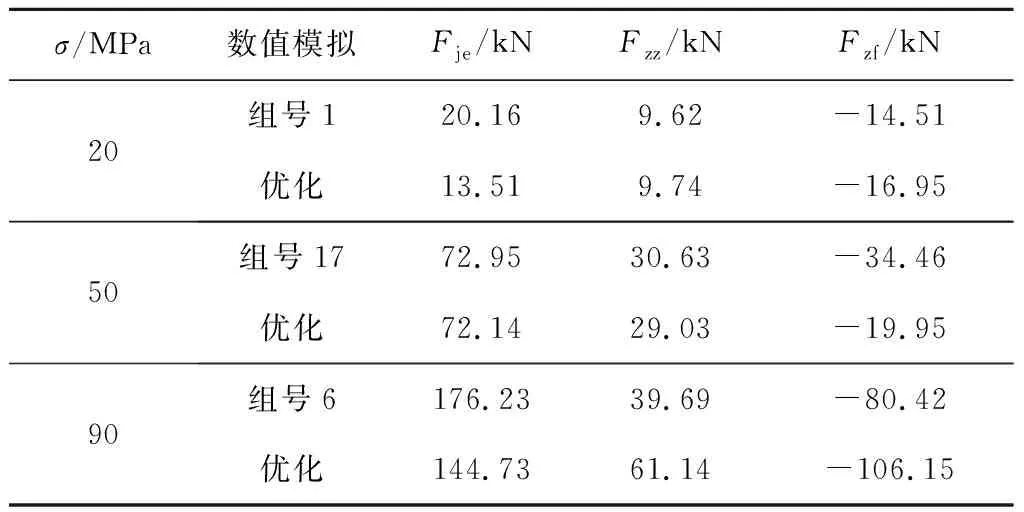
表8 优化参数数值模拟对比

由表3、4、8可知，当σ=20 MPa时，与正交数值模拟组号1相比，多目标遗传算法优化得到的参数进行数值模拟，碟盘所受最大载荷小15.92%。径向载荷峰值均值小32.98%。

当σ=50 MPa时，与正交数值模拟组号17相比，多目标遗传算法优化得到的参数进行数值模拟，径向载荷峰值均值相比无明显变化，负轴向载荷峰值均值小42.11%。当σ=90 MPa时，与正交数值模拟组号6相比，多目标遗传算法优化得到的参数进行数值模拟，径向载荷峰值均值小17.87%。

4 结 论

(1)通过变异系数法确定各评价指标的权重，TOPSIS法对18组数值模拟进行综合评价。综合评价值最小时为最优参数组合，当煤岩强度20 MPa时，第1组综合评价值最小；当煤岩强度50 MPa时，第17组综合评价值最小；当煤岩强度90 MPa时，第6组综合评价值最小。

(2)通过极差分析法获得了对碟盘截割煤岩性能影响的程度，由大到小依次为煤岩强度、振动幅值、碟盘齿数、振动频率、进给速度。

(3)与18组数值模拟中综合评价值最优的组号相比，当σ=20 MPa时，多目标遗传算法寻优参数得到在z=60，v=200 mm/s，f=50 Hz，A=3 mm时，碟盘所受最大载荷峰值均值小15.92%，径向载荷峰值均值相比小32.98%；当σ=50 MPa时，多目标遗传算法寻优参数后得到在z=60，v=200 mm/s，f=30 Hz，A=1 mm时碟盘所受最大载荷峰值均值无明显变化；当σ=90 MPa时，多目标遗传算法寻优参数后得到在z=60，v=200 mm/s，f=30 Hz，A=1.5 mm时，碟盘所受径向载荷峰值均值小17.87%。