改进变分模态分解的铣刀磨损状态监测方法

周广林， 舒贝贝， 刘培江

(黑龙江科技大学 机械工程学院， 哈尔滨 150022)

0 引 言

铣刀在进行金属切削时，不可避免会发生磨损及破损，对零件加工的质量产生影响，严重时会损坏机床，因此，监测铣刀状态尤为重要。目前，通过提取监测信号有用特征信息，是实现刀具状态监测的关键。由于声音信号采集方便、响应速度快，常被用作监测信号。但是，声音信号大多表现为非平稳特性，易受环境噪声影响，使其所包含的有用特征较难提取，目前，常用的信号处理方法有快速傅里叶变换(FFT)、经验模态分解[1](EMD)、集合经验模态分解[2](EEMD)、小波变换等[3]，基本都存在一些不足。EMD分解的信号存在模态混叠，EEMD在处理信号过程中会引入残余噪声和带噪声的信号，重构后可能产生不同的模态数量，小波变换的效果容易受小波基选择影响。变分模态分解(VMD)是由Konstantin等[4]提出的。相比于EMD、EEMD，VMD可更好解决信号分解的模态混叠、边界效应问题，对噪声具有较好的鲁棒性。目前，该方法在信号分解及特征提取[5]、铣刀状态识别[6-7]等方面已经得到了较好应用，然而，VMD算法的分解效果易受模态数k和二次惩罚因子α取值影响。针对此不足，任刚等[8]采用改进自适应遗传算法IAGA对VMD的参数进行优化，实验验证了该方法的有效性。

鉴于铣刀铣削的声音信号特征提取困难且VMD在信号分解上存在的不足，笔者利用自适应遗传算法对VMD的模态数k和二次惩罚因子α进行优化改进，将改进的VMD应用到铣削声音信号的分解及特征提取上，结合LS-SVM实现对铣刀磨损状态监测，通过实验验证所提方法的有效性。

1 变分模态分解

1.1 基本原理

变分模态分解的数学理论基础是在约束条件下求解变分问题。该方法通过不断迭代寻找一种模态uk的集合，且这些模态分量估计带宽之和最小，能够最佳重构给定的输入信号f(t)，且每个模态都限制在一个在线估计的中心频率ωk附近，从而完成信号频带的自适应分解。

在VMD中，基于调制标准，将本征模态函数(IMF)定义一个调幅—调频信号，表达式为

uk(t)=Ak(t)cosφk(t)，

(1)

式中:Ak(t)——瞬时振幅，V；

φk(t) ——瞬时相位，rad；

k——IMF分量个数。

假设Ak(t) ≥ 0且φk(t)为非递减函数，对每个模态uk(t)进行Hilbert变换求其解析信号以获得单边频谱，再调谐到各自估计的中心频率的基带上。对解调后的信号进行梯度L2范数平方，可构造约束变分问题的模型为

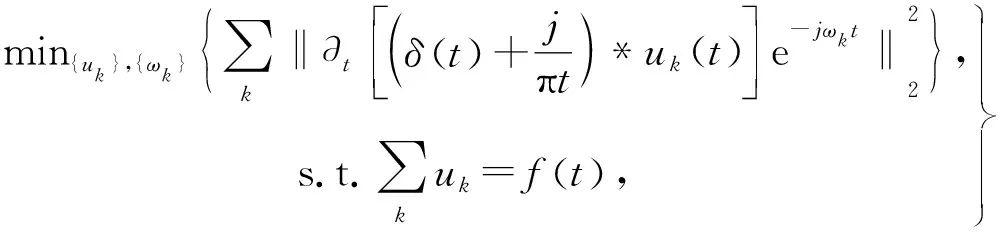
(2)

式中:δ(t)——单位脉冲函数；

*——卷积符号。

为求解约束变分问题，在此使用二次惩罚项α和拉格朗日乘数λ算子，以使求解变成无约束变分问题。构造的拉格朗日算子为

(3)

1.2 改进变分模态分解

VMD算法的分解效果易受模态数k和二次惩罚因子α的取值影响，且VMD分解的声音信号较复杂，含有较多噪声，通过人为设置这两个参数会对信号分解带来不确定性误差。若k值过大或过小，会导致声音信号过分解或分解不充分，使一个或几个额外的IMF分量主要由噪声组成或者造成模态混叠现象；同样，二次惩罚因子α的取值也会影响IMF分量的带宽，因此，采用有效参数选择方法，优化选择这两个参数，对于声音信号的分解至关重要。笔者以多尺度排列熵[9]为目标函数，利用自适应遗传算法[10]优化VMD的参数。具体参数优化步骤如下：

步骤1对VMD的参数组合[k,α]进行染色体初始化编码，形成初始种群。

步骤2利用个体的参数组合对信号进行VMD分解，求分解后的各模态函数(IMF)的多尺度排列熵值，计算相应适应度，令多尺度排列熵的最小值为局部极小值。

步骤3不断进行种群的选择、交叉、变异，比较局部适应度值大小，寻找全局最小值。

步骤4迭代终止，确定最终的最优个体，即参数组合[k,α]。

2 磨损状态监测实验

2.1 监测流程

实现铣刀磨损状态的识别监测，需要在铣刀切削工件达到不同磨损状态时采集铣削声音信号，完成铣刀磨损状态样本的构建及模型训练。首先，实验以铣刀从新刀开始持续切削工件直到达到急剧磨损状态为止，仿照铣刀磨损的过程，同时，使用传声器对铣削声音信号进行采集。然后，利用改进的VMD算法分解声音信号，提取与刀具磨损状态密切相关的信号边际谱能量熵比构成特征向量样本，再输入到最小二乘支持向量机中进行模型训练，运用训练好的模型对铣刀磨损状态进行识别。铣刀磨损状态识别监测流程，如图1所示。

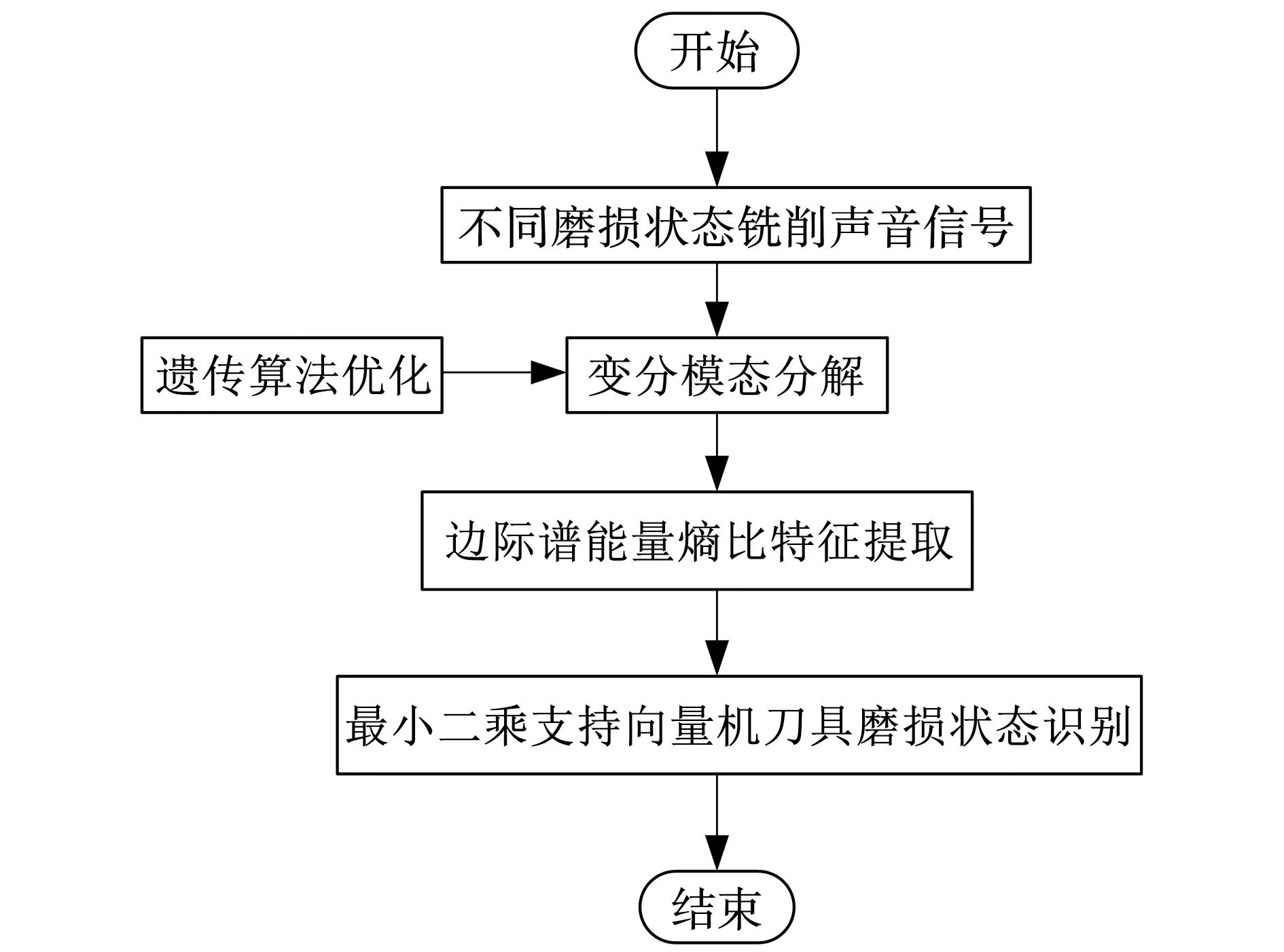
图1 铣刀磨损状态监测流程Fig. 1 Flow of tool wear condition monitoring

2.2 实验装置与实验条件

铣削声音信号采集系统是基于LabVIEW软件结合铣床、传声器、数据采集卡和三刃立铣刀等搭建的，其原理示意如图2所示。其中，机床为汉川XH714D型立式加工中心，主轴转速为8 000 r/min，传声器型号为AWA14423，工作频段为10～20 kHz；数据采集卡型号为NI-USB-6002，最大采样率为50 KS/s，信号采样频率设定为44 100 Hz；刀片材料为PVD涂层硬质合金(YBG205)；工件材料为45#钢，尺寸为200 mm×200 mm×50 mm。切削速度为220 m/min，进给量为0.1 mm/r，径向切宽为0.15 mm，轴向切深为5 mm。对于硬质合金刀具，国际标准ISO规定以其后刀面δb达到0.3 mm为其磨钝标准。实验根据铣刀和工件材料，将铣刀磨损设置为三种状态：初期磨损状态(δb≤ 0.15 mm)、正常磨损状态(0.15<δb<0.3 mm之间)、急剧磨损状态(δb≥ 0.3 mm)。

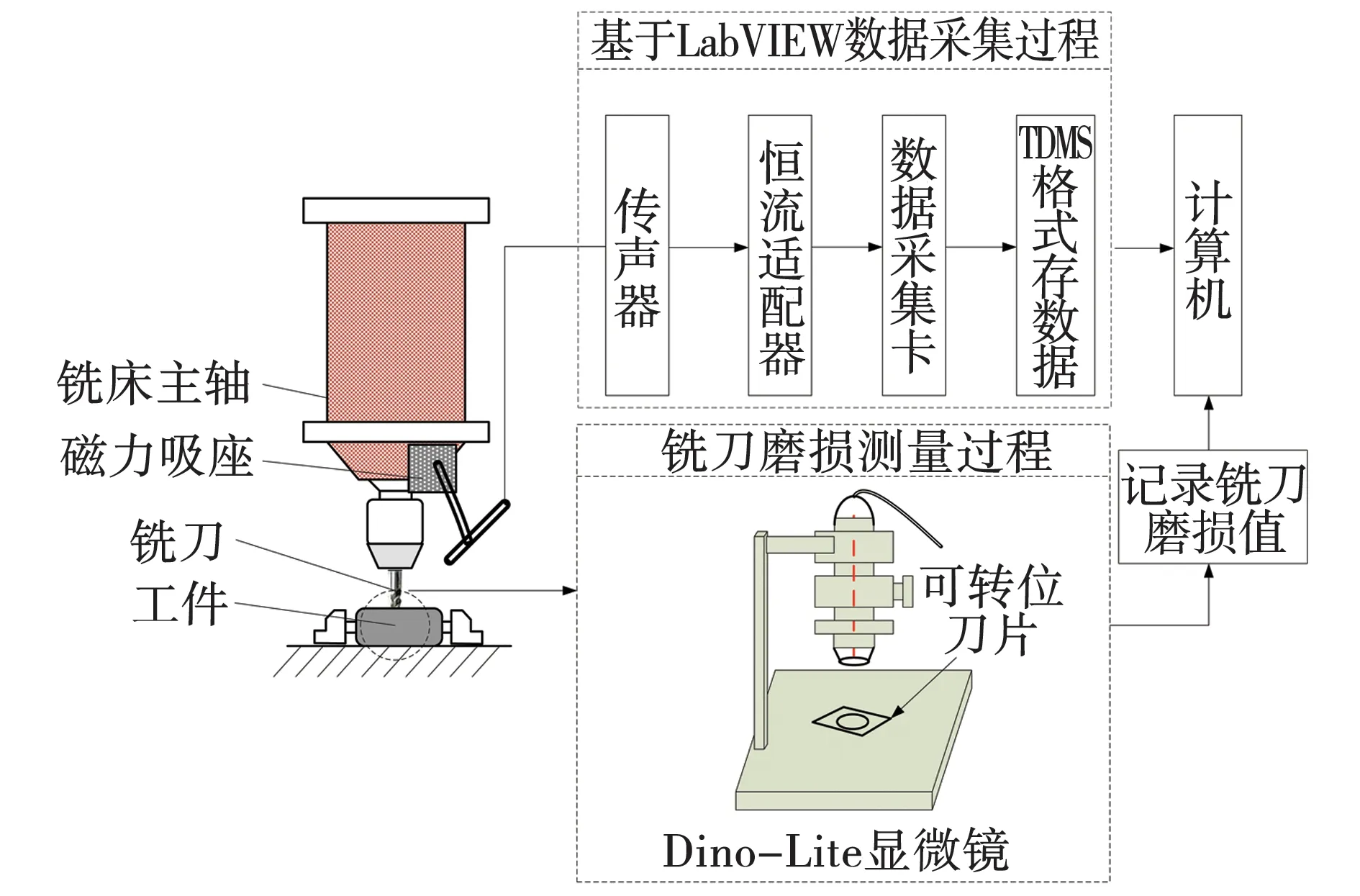
图2 实验系统原理示意Fig. 2 Schematic of test system

铣削过程采用顺铣加工，不加切削液，将铣刀从新刀开始铣削45#钢直到急剧磨损状态为止。实验过程中，铣刀每切削一个200 mm的距离就采集一组声音数据，停机利用Dino-Lite显微镜测量一下铣刀的后刀面磨损量δb值并记录，以建立铣刀的磨损状态与声音信号的对应关系。按照此步骤，分别采集铣刀在三种状态下各40组声音数据，每组数据包含4 900个点。

3 实验结果与分析

3.1 改进VMD的铣削声音信号分解

实验采集到的铣刀在3种磨损状态下的铣削声音信号波形如图3所示。从图3可以看出，铣削声音信号具有非平稳特性，内含噪声干扰，且3种状态的声音信号在波形上区别并不明显，从中很难判断出铣刀所处磨损状态。因此，需要对信号进行处理，以提取出能表征刀具磨损的特征信息。利用VMD算法对信号进行分解处理，在信号分解前，优化选择VMD的参数。

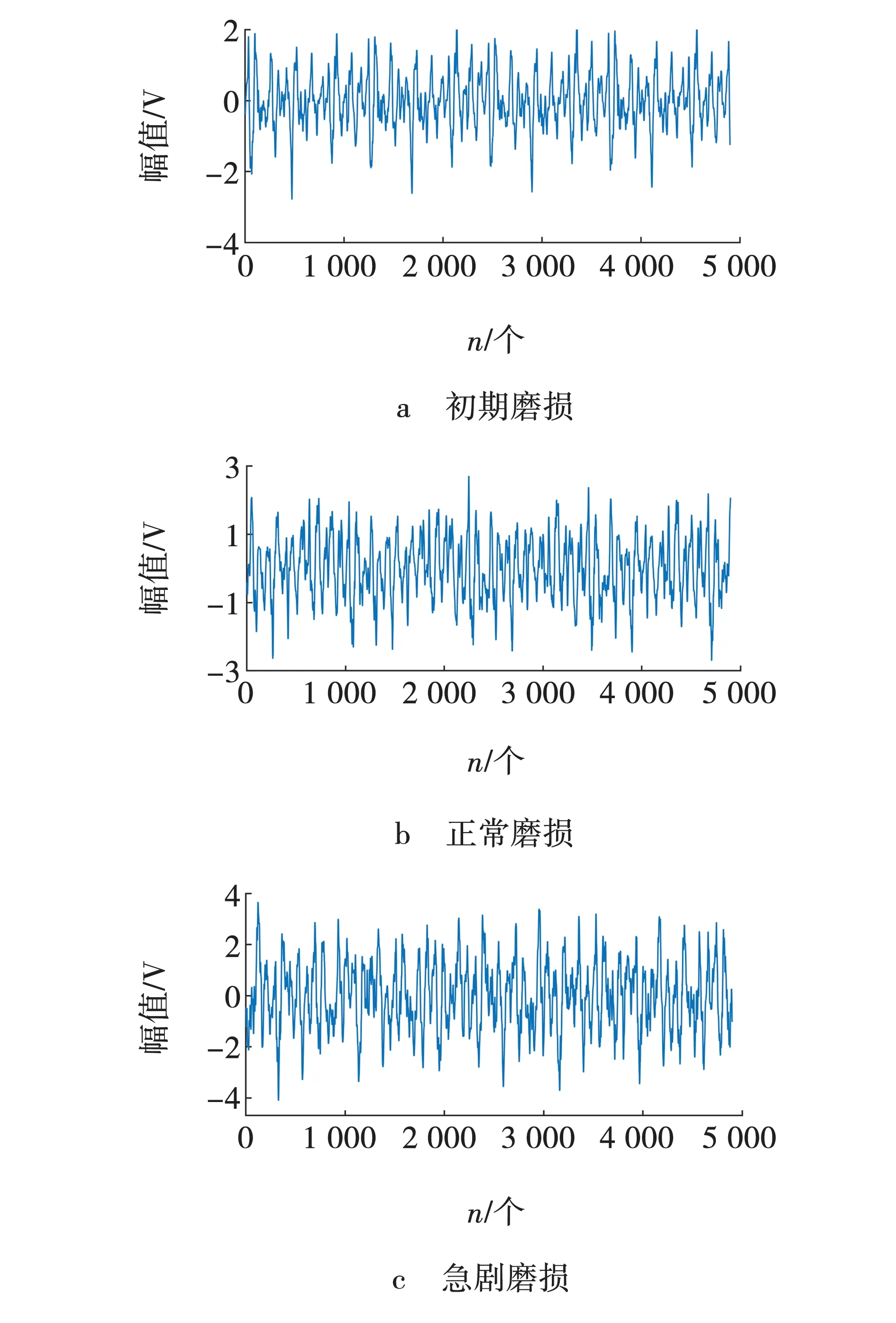
图3 3种状态铣削声音信号波形Fig. 3 Milling sound signal waveform in three states

利用自适应遗传算法GA优化VMD分解初期磨损状态信号时的参数k和α，其中，设置k的取值范围为[2, 9]，α的取值范围为[500, 7 000]，遗传算法的最大迭代次数nm为30，种群数量为20，交叉概率和变异概率的调整系数为1.0和0.5。图4为VMD参数优化训练过程。从图4可以看出，在第14代时，出现最佳适应度值0.640，此时对应的最优参数组合为[8, 5 237]，即可设VMD的模态数k为8，惩罚因子α为5 237。利用同样的参数优化方法，对VMD分解其余两种状态信号时的参数进行优化，优化结果如表1所示。

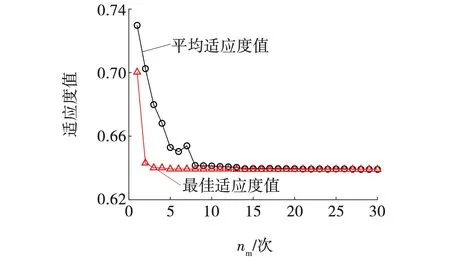
图4 VMD参数优化训练过程Fig. 4 VMD parameter optimization training process

根据表1中VMD优化参数，对3种状态下声音信号进行分解，结果如图5 ～ 7所示。从图5 ～ 7可以看出，铣削声音信号被VMD分解成不同频率段本征模态函数IMF，每种IMF分量之间没有发生模态混叠现象；铣削声音信号IMF1与IMF2分量在三种状态下波动程度是最为明显的，也是区别最大的，而对于其它IMF分量来说，随着频率逐渐增加，可区分性逐渐降低；有关铣刀磨损信息的频率成分被成功分解出来，表明该方法在声音信号分解上具有适用性和有效性。

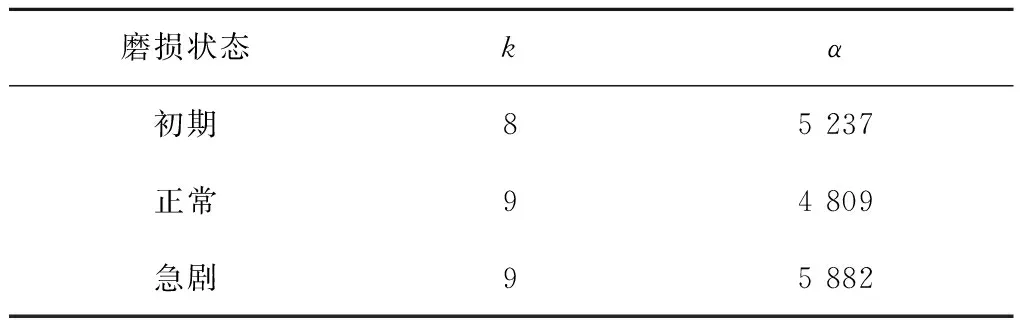
表1 不同磨损状态下铣削声音信号的VMD参数优化结果

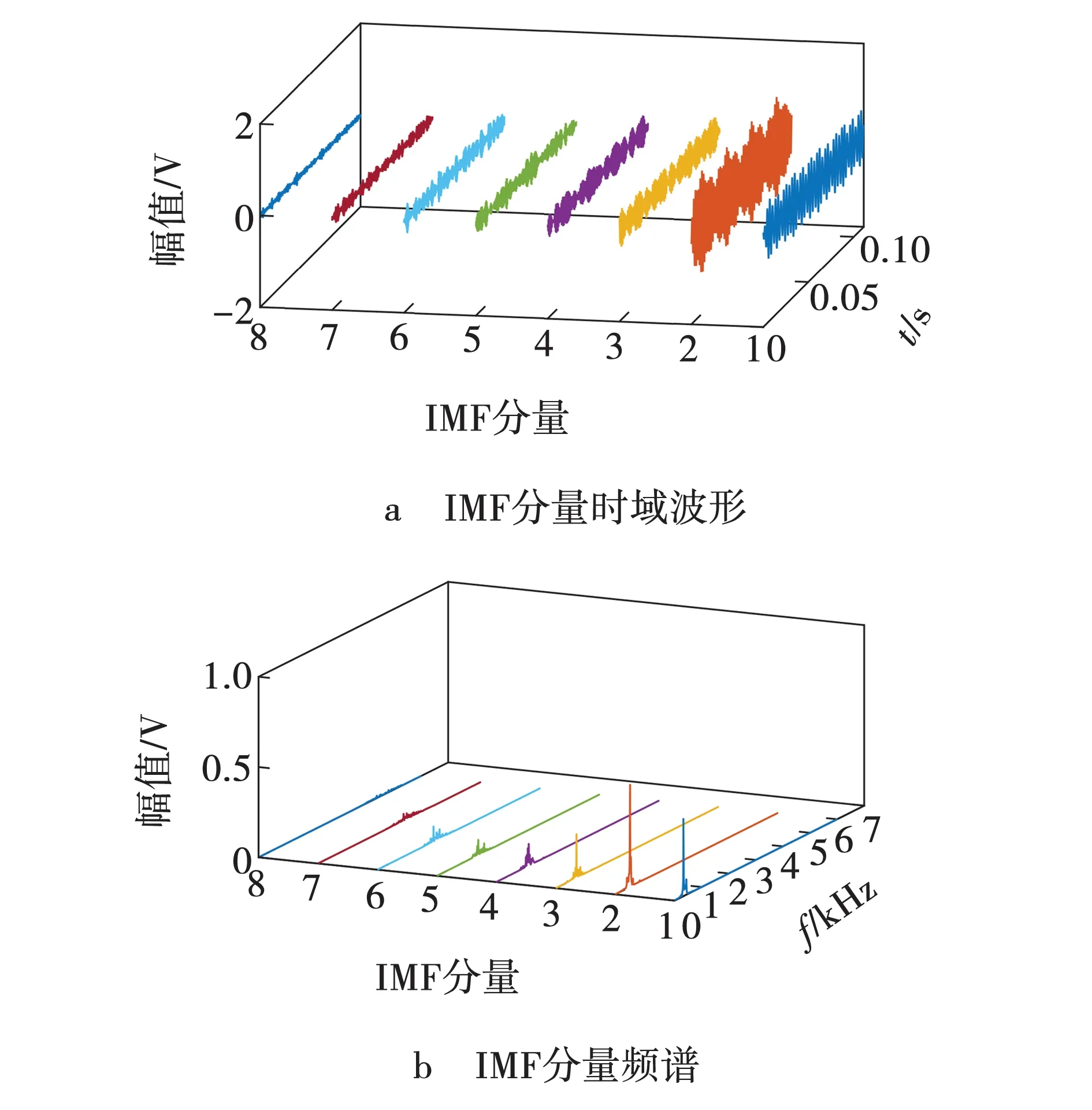
图5 初期磨损状态下声音信号的VMD分解结果 Fig. 5 VMD decomposition result of sound signal under initial wear state

3.2 边际谱能量熵比特征向量提取

能量熵比是能量与熵的比值，IMF分量边际谱能量熵比的特征提取是通过对分量集合进行希尔伯特变换，获得边际谱，进而提取边际谱的熵值和分量能量，构成能量熵比特征向量矩阵。

对声音信号经VMD分解后的若干有用IMF分量分别进行希尔伯特(Hilbert)变换，可获得相对应的解析信号，其表达式为

zi(t)=ai(t)ejφi(t)，i=1,2,…,k，

图6 正常磨损状态下声音信号的VMD分解结果Fig. 6 VMD decomposition results of sound signals under normal state of wear

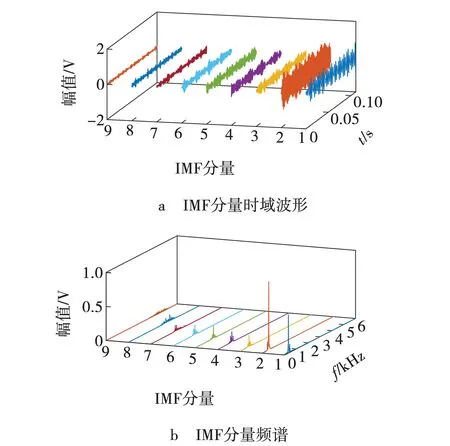
图7 急剧磨损状态下声音信号的VMD分解结果 Fig. 7 VMD decomposition result of sound signal under abrupt state of wear

(4)

式中:ai(t)——解析信号的瞬时幅值，V；

φi(t) ——解析信号的瞬时相位，rad。

原信号的Hilbert时频谱，可表示为

(5)

对时频谱H(w,t)在时间上进行积分，可获得Hilbert边际谱，其表达式为

(6)

由式(6)可定义第i个IMF分量的边际谱能量为

(7)

式中，Ei——单个IMF分量的边际谱在频率上的幅值平方累加和。

根据信息熵的原理，可定义IMF的边际谱熵为

(8)

式中，pr——第r个频率w所对应的幅值出现的概率。

(9)

由式(7)、(8)可求得，各个本征模态函数IMF的边际谱能量熵比为

(10)

根据式(10)可构造VMD的边际谱能量熵比特征向量为

S=[s1,s2,…,sk]。

(11)

利用上述特征提取方法对声音信号分解后的IMF分量进行Hilbert变换，变换后信号边际谱如图8所示。从图8可以看出，声音信号的频率成分主要分布在300～2 000 Hz频段范围内；3种磨损状态下的声音信号IMF分量边际谱幅值波动程度及能量大小是明显不相同的，随刀具磨损程度加深，幅值波动程度加深，能量增加，可提取边际谱相关特征来反映铣刀磨损的变化情况。

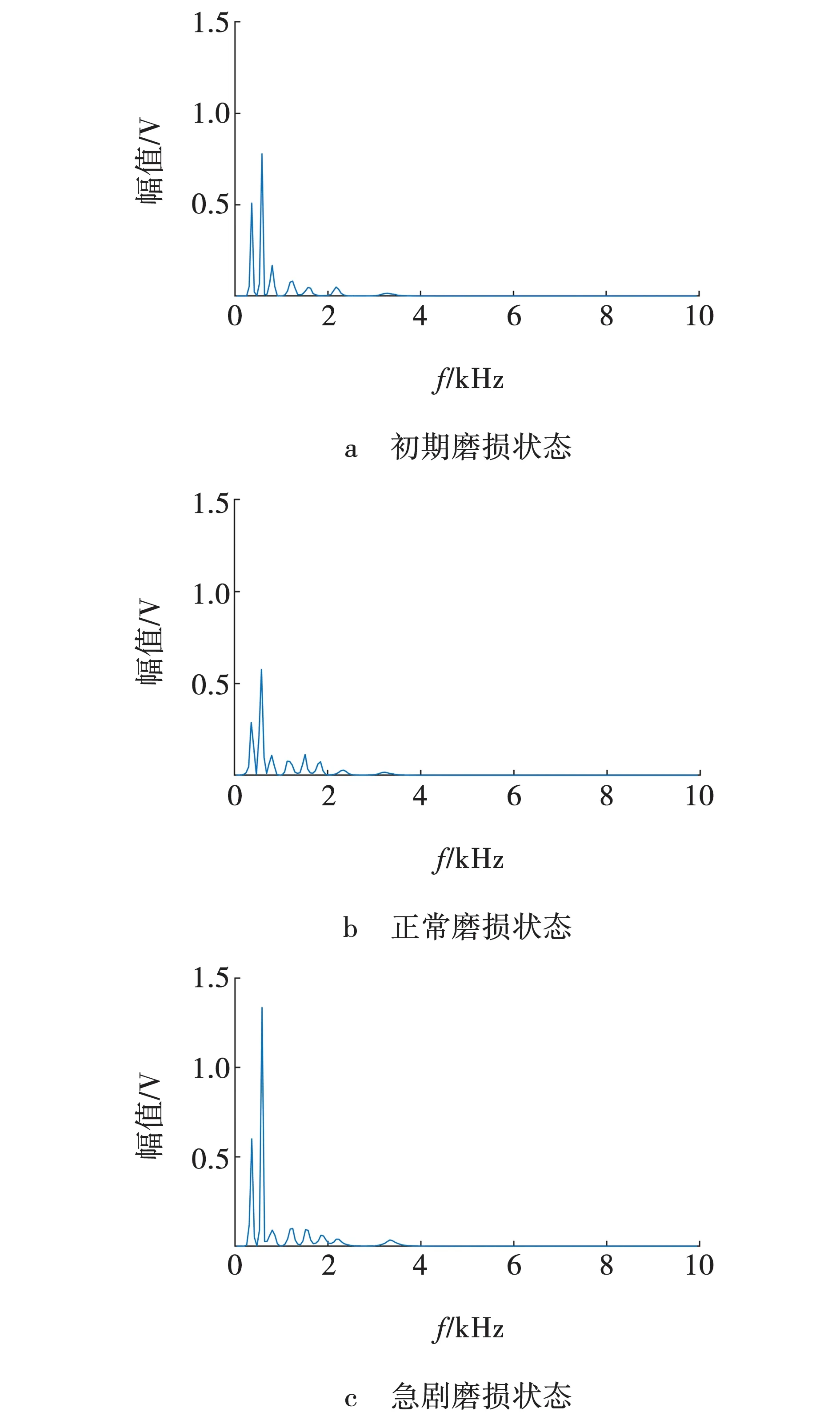
图8 铣刀的铣削声音信号的IMF分量边际谱Fig. 8 IMF marginal spectrum of milling sound

IMF的边际谱整体波动程度可用信息熵反映，IMF分量的能量分布情况可用能量大小表示，因此，可通过IMF分量的边际谱能量和信息熵的比值来共同反映铣刀在不同磨损状态下的铣削声音信号变化情况。与单一特征值相比，这样既可避免不同状态下信号因能量相近而不能准确区分，又能避免噪声对信号熵值的干扰。信号边际谱的前六个波峰相对较大，可区分性高，可用来构造特征向量，构成结果如表2所示。从表2可以看出，不同磨损状态下声音信号的同一种IMF分量边际谱能量熵比有明显区别，具有可分性；其次，模态函数分量IMF1、IMF2与IMF4～IMF6的能量熵比随着刀具磨损程度的不断加剧，呈现上升趋势。因此，可以将声音信号的IMF能量熵比作为铣刀磨损的状态特征，输入到LS-SVM模型中去监测信号能量熵比变化，实现对刀具磨损的状态监测。

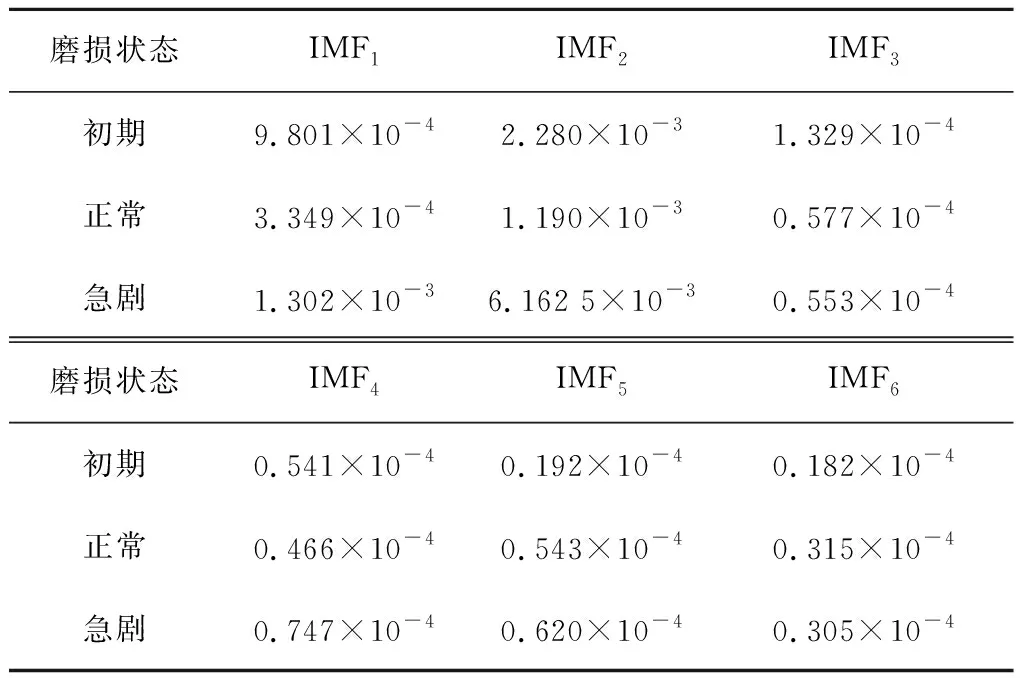
表2 IMF分量边际谱能量熵比

3.3 铣刀磨损状态识别

最小二乘支持向量机(LS-SVM)是由Suykens等[11]提出的。与BP神经网络分类识别方法相比，LS-SVM的识别精度高、鲁棒性好、具有泛化能力强、全局收敛、不依赖经验信息等突出优点。因此，可将LS-SVM作为铣刀磨损状态的监测模型对特征向量进行训练和识别。

提取的正常磨损、初期磨损和急剧磨损三种状态的特征向量共构成了一个120×6的特征向量矩阵，其中，每种磨损状态都有40组特征向量。将初期、正常及急剧磨损状态的类别标签依次计为1、2、3。从120组数据中选择60组数据用于LS-SVM模型训练，其中，包括初期磨损21组样本，正常磨损20组样本，急剧磨损19组样本，其余60组作为测试样本。LS-SVM对测试样本识别结果如图9所示。

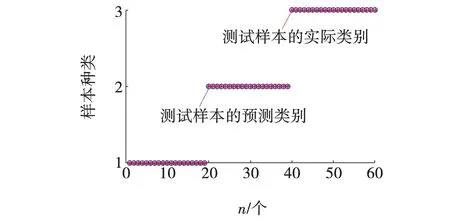
图9 最小二乘支持向量机识别结果 Fig. 9 Recognition results of least squares support vector machine

从图9可以看出，三种状态测试样本的识别准确率为100%，这表明采用改进VMD的边际谱能量熵比结合LS-SVM方法在铣刀状态识别上可行。为进一步验证文中提取的边际谱能量熵比特征值在铣刀磨损状态监测上的优越性，利用LS-SVM分别对改进VMD提取的信号边际谱能量熵、边际谱熵、边际谱能量的特征向量进行识别精度统计，结果如表3所示。由表3可见，VMD所提取的边际谱能量熵比识别准确率最优。

表3 测试精度

4 结 论

(1)以铣刀铣削45#钢达到不同磨损状态为实验对象，研究基于铣削声音信号的刀具磨损状态监测方法，改进VMD边际谱能量熵比与LS-SVM相结合的铣刀磨损状态监测方法可以有效识别出铣刀的三种磨损状态。

(2)自适应GA优化VMD方法可以将铣削声音信号成功分解为若干个不同频率段的IMF分量，每种分量之间未发生模态混叠现象，且有关铣刀磨损的有用成分能被分解出来。这表明该方法在声音信号分解上具有适用性。

(3)与边际谱能量熵、边际谱熵和边际谱能量特征值相比，边际谱能量熵比可以从能量和熵两方面来共同反映铣刀磨损状态的变化，利用该特征判别铣刀磨损状态，准确率可达100%。