GUM法和MCM法对饲料粗蛋白含量测量不确定度评定的比较

余舒宁，高志存，崔惠娟，石露莎，高 芸

（红河州兽药饲料监察所，云南 蒙自661199）

测量不确定度是表征赋予被测量值分散性的非负参数，是判定测量结果可信度的参数[1]。测量不确定度的评定方法通常采用GUM法[1]；蒙特卡洛（MCM）法是一种新的评定不确定度的方法[2]，提供了比较和验证GUM法的一种途径[1-2]。JJF1059.1—2012《测量不确定度评定与表示》中对测量不确定度评定的方法简称GUM法，GUM法是采用“不确定度传播律”传播输入量的最佳估计值和其标准不确定度获得输出量的估计值及其测量不确定度的方法[1-2]。蒙特卡洛法缩写为MCM，是一种概率传播方法，即通过对输入量Xi的概率密度函数（PDF）离散抽样，由测量模型传播输入量的概率分布，计算获得输出量Y的概率密度函数（PDF）的离散抽样值，进而由输出量的离散分布数值获取输出量的最佳估计值、标准不确定度和包含区间[2]。本文以饲料中粗蛋白含量测定为例，采用GUM法和MCM法对饲料中粗蛋白含量测定结果的不确定度进行评定，对两种方法的评定结果进行比较验证，并对测定过程中不确定度产生的来源进行分析，找出影响测量不确定度的主要因素，以期为实验室质量控制提供科学依据，保证测定结果的质量。

1 材料与方法

1.1 仪器

AG-204型电子天平，瑞士梅特勒公司产品；Kjeltec 8200型凯氏定氮仪，福斯分析仪器公司产品；Titrette 25 mL数字瓶口滴定器，德国BRAND公司产品。

1.2 试剂

硫酸、无水硫酸钠、硫酸铜均为分析纯，0.101 8 mol·L-1盐酸滴定液，400 g·L-1氢氧化钠，20 g·L-1硼酸，甲基红-溴甲酚绿混合指示剂。

1.3 样品及测定方法

样品为仔猪配合饲料，按GB/T 6432—2018《饲料中粗蛋白的测定 凯氏定氮法》测定[3]，用全量法，数据为两平行样测定结果，测量相关参数见表1。

表1 饲料中粗蛋白含量测定的数据

2 GUM法评定不确定度

2.1 测量模型与不确定度来源分析

根据测定方法和试验原理，配合饲料中粗蛋白含量可用以下公式计算：式中：w为试样中粗蛋白的含量（%）；VHCl为试样消耗盐酸滴定液的体积（mL）；V0为空白消耗盐酸滴定液的体积（mL）；CHCl为盐酸滴定液的浓度（mol·L-1）；m样为试样质量（g）；0.014为氮的毫摩尔质量（g·mmol-1）；6.25为氮换算粗蛋白的平均系数。考虑重复性因子rep，上述公式可写成：

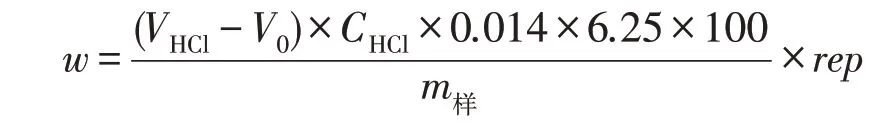
式中：rep为方法重复性因子。

这就是凯氏定氮法测定饲料中粗蛋白含量的测量模型。由测量模型得知，该测量过程中不确定度有以下几方面：重复测定的不确定度；试样称量的不确定度；盐酸滴定液浓度的不确定度；盐酸滴定液消耗体积的不确定度。

2.2 GUM测量不确定度的评定

2.2.1 重复测定的不确定度u(rep)[4]

根据表1中的平行测定结果，用极差法来评定两次测定的不确定度：

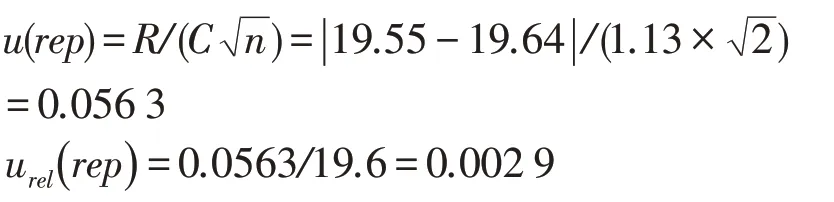
2.2.2 试样称量的不确定度u(m)

2.2.3 盐酸滴定液浓度的不确定度u(c)

2.2.4 盐酸滴定液消耗体积的不确定度u(V-V0)

2.2.5 饲料中粗蛋白含量的相对合成标准不确定度

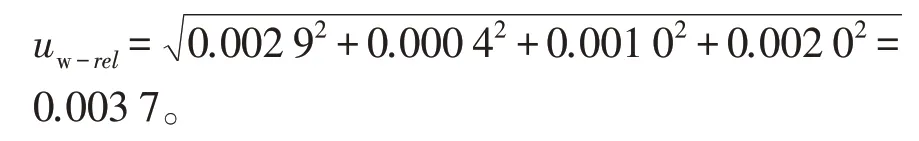
2.2.6 饲料中粗蛋白含量的合成标准不确定度：

2.2.7 扩展不确定度

取k=2时，U=k×uw=2×0.072 5%=0.1%。

2.2.8 GUM法的不确定度

评定饲料中粗蛋白含量的不确定度，测定结果的完整表述为：w=（19.6±0.1）%，k=2。

3 MCM法评定不确定度

3.1 Matlab简介

MCM是实现概率分布传播的一种数值方法，MCM的关键是对所有输入量的PDF进行随机抽样，用数学方法产生随机数，Matlab是一款功能强大的数值计算软件，完全能胜任产生随机数的功能。本文采用MathWorks公司的Matlab软件[7-8]编写MCM程序。

3.2 测量模型及经验参数

式中：w为试样中粗蛋白的含量（%）;VHCl为试样消耗盐酸滴定液的体积（mL）；V0为空白消耗盐酸滴定液的体积（mL）；CHCl为盐酸滴定液的浓度（mol·L-1）；m样为试样质量（g）；0.014为氮的毫摩尔质量（g·mmol-1）；6.25为氮换算粗蛋白的平均系数；rep为方法重复性因子。

盐酸滴定液消耗的体积V与温度和测量系统的校准有关：

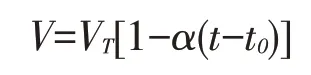
式中，α为水的膨胀系数（℃-1）；t为实验室温度（℃）；t0为校准时温度。

因此，在MCM中测量模型变为：

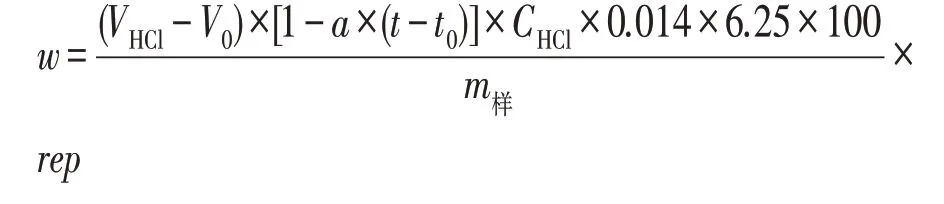
据GUM评定引用相应参数计算后列于表2。

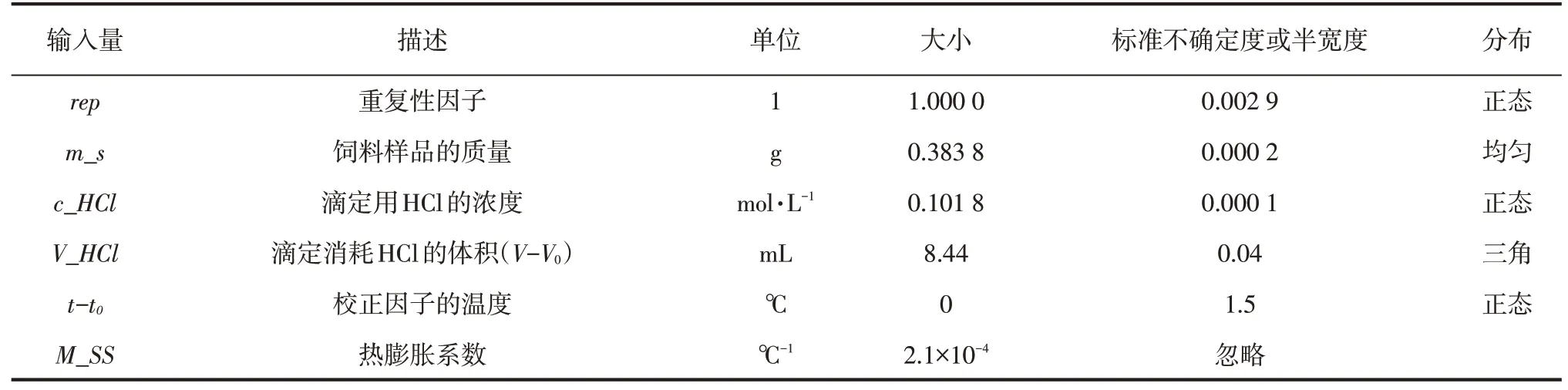
表2 输入量的大小、不确定度和设定的分布

3.3 MCM实施的Matlab程序

据周桃庚[4]、刘存成等[5]的MCM的Matlab程序，略作改动及注释后如下：

MCM得到的平均值19.6%，标准不确定度为0.07%，95%概率的包含区间为[19.5%,19.7%]，扩展不确定度U95=0.07%×2=0.1%（见图1）。

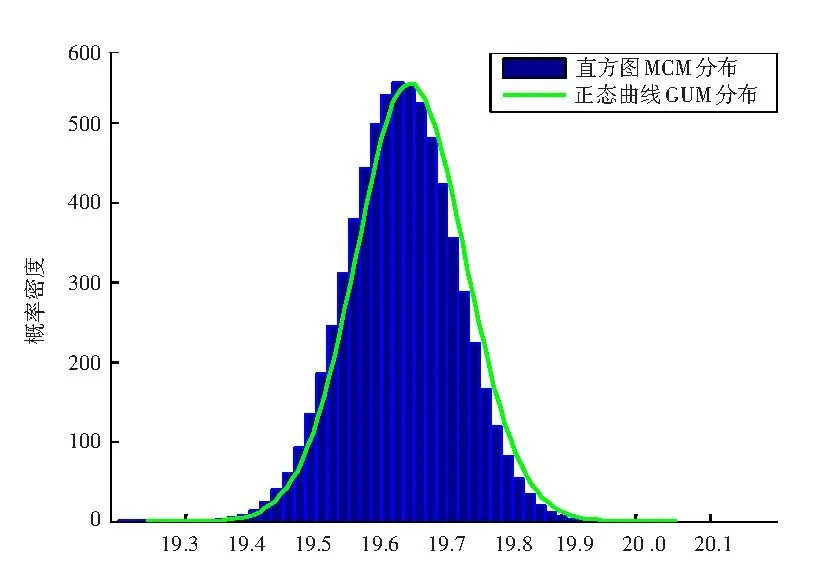
图1 饲料粗蛋白含量的概率密度分布

3.4 采用MCM法评定饲料中粗蛋白含量的不确定度

测定结果完整表述为：w=（19.6±0.1）%。

4 GUM法与MCM法不确定度评定结果的比较验证

对GUM法和MCM法评定结果进行比较，当dlow=|y-u(y)-y low|及d high=|y+u(y)-y high|均小于δ时，GUM法可通过验证[7-8]。GUM法与MCM法不确定度评定结果见表3。由表3可知，MCM法对GUM法不确定度框架通过了验证，且MCM与GUM两者评定的结果一致，达到预期。

表3 GUM法与MCM法不确定度评定结果比较

MCM评定不确定度虽然是纯数学方法，但还是以GUM法为基础，所有的经验参数值都是以试验数据为依据，进行仿真数学模拟，结果可信度是有保障的。

5 分析与结论

通过上述评定过程可以看出，采用凯氏定氮法测定饲料中粗蛋白含量，从各个不确定度分量的计算结果可以看出，分量中最大的是重复测定的不确定度，其次为盐酸滴定液消耗体积的不确定度。以平行样数据（n=2）评定不确定度，结果准确性会差一些。要准确评定不确定度，应按标准要求[1-2]，试验平行样不少于10次（n≥10），用贝塞尔法计算标准差，评定不确定度，通过增加平行测定次数可以有效降低重复测定的不确定度。但现有检测技术要求化学试验中检测样品基本都是检测平行样（n=2），这种用平行样评定不确定度的方法可粗略评估出不确定度，作为初步的判断，在工作中有一定的实用价值[10-11]。