融合差分进化思想的自适应人工蜂群算法

封 硕，刘 琨

(1.长安大学 机械工程学院 陕西 西安 710061；2.长安大学 理学院 陕西 西安 710061)

0 引言

人工蜂群算法(artificial bee colony，ABC)是模仿蜜蜂群体采蜜行为提出来的一种启发式智能优化算法，与遗传算法(genetic algorithm，GA)[1]、差分进化算法(differential evolution，DE)[2]、蚁群算法(ant colony optimization，ACO)[3]和粒子群算法(particle swarm optimization，PSO)[4]相比，由于ABC算法具有参数少、精度高和结构简单易实现等优点，近几年来受到广泛的关注，并被应用到数据挖掘[5]、生产调度[6]和信息处理[7]等领域。

与其他优化算法相似，ABC算法在解决复杂优化函数时，存在收敛速度慢、算法后期种群多样性下降及易陷入局部最优解等缺点。许多学者对其进行改进，主要在提高算法的收敛速度、增加种群的多样性以及改进算法的寻优机制等方面尝试。Gao等提出了基于差分进化算子的改进人工蜂群算法[8]；Zhu等受到粒子群算法的影响，利用最优解指导雇佣蜂的局部搜索[9]；魏锋涛等引入量子行为模拟蜂群求解过程[10]；赵玉霞等受到猫群思想搜索过程启发，对较优解与较差解分别执行搜寻与跟踪模式[11]。

以上研究主要改进了搜索公式，提升了算法的寻优效率。但仍存在不足之处：首先，在初始化阶段中随机产生初始种群，其随机性导致种群的多样性不足，不利于算法求得潜在最优解。其次，雇佣蜂搜索过程中仅利用先前个体的信息产生候选解,这种机制利于勘探不利于开发。最后，算法后期种群多样性下降，导致算法收敛速度慢。为解决以上问题，本文在初始化阶段利用反向学习策略，根据种群的适应度值贪婪选择较优的初始个体，扩大种群的多样性，提高解的质量，加强算法跳出局部最优解的能力。同时，本文将雇佣蜂搜索过程与差分进化算法融合，并加入自适应策略平衡算法的勘探与开发能力，加快人工蜂群算法的收敛速度。最后，在侦查蜂阶段中引入混沌序列，增加种群的多样性。

1 改进的人工蜂群算法

1.1 基于反向学习策略的初始化阶段

Tizhoosh提出反向学习策略(opposition-based learning，OBL)[12]，并将其应用到神经网络及强化学习中，主要思想是在取值区域内同时考虑当前个体和与它方向相反的个体，质量更优的个体进入下一代。Rahnamayan等从数学的角度证明了与随机产生候选解的方式相比[13]，反向学习策略不但可以提高种群的多样性，还可以提高解的质量，在一定程度上避免算法陷入局部最优。基于反向学习策略的反向初始种群的公式为

(1)

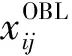
1.2 融合差分进化思想的自适应搜索阶段

Gao等受到DE算法的启发[8]，基于差分进化算子与雇佣蜂搜索阶段的性质，提出了ABC/best/1算法，本文算法在ABC/best/1算法的基础上加入自适应策略，平衡算法的勘探与开发能力，以加快算法的收敛速度，

vij=a(t)xjbest+(1-a(t))R(xij-xkj)，

(2)

(3)

式(2)中：a(t)表示自适应参数；xjbest表示当前种群中的最优解；k∈{1,2,…，SN}，j∈{1,2,…，D}，k和j都是随机选取的，且k≠i。式(3)中：iter表示当前迭代次数；Maxcycle表示最大的迭代次数。算法初期阶段应侧重于勘探能力，此时自适应参数取较小值；随着迭代次数的增加，算法后期阶段应侧重于开发能力，此时自适应参数取较大值。

1.3 基于混沌序列的侦查蜂阶段

文献[11]指出，算法后期食物源的位置相似度高，导致位置更新速度慢；算法后期的多样性下降，导致搜索能力下降。混沌[14]是一种非线性现象，具有非周期性、遍历性、随机性等特点，即混沌序列在取值区域内不重复地遍历所有状态。本文算法在侦查蜂阶段中引入Logistic混沌序列，增加种群的多样性，加快算法的收敛速度。Logistic混沌序列的主要思想为

Ci+1=μ×Ci×(1-Ci)，

(4)

式中：μ为控制参数，当μ=4时，公式(4)处于完全混沌状态；Ci表示第i次的混沌映射变量，Ci是(0,1)上均匀分布的随机数且Ci≠0.25,0.5,0.75,i=0,1，…，M，为混沌序列的长度；初始混沌变量C0=0.32。

基于Logistic混沌序列侦查蜂搜索公式为

xij=ximin+Cj(ximax-ximin)。

(5)

1.4 本文算法的步骤

综上所述，本文提出的融合差分进化思想的自适应ABC 算法主要步骤如下。

Step1 在D维空间中生成SN个初始解,根据初始种群与反向种群的适应度值排序，贪婪选择SN个个体作为初始种群；

Step2 雇佣蜂在初始位置的附近利用搜索公式(2)进行局部邻域搜索，贪婪选择适应度值较优的食物源；

Step3 全部的雇佣蜂完成一次局部搜索后，观察蜂根据雇佣蜂提供的适应度值，按照概率Pi选择食物源，并在该食物源附近进行邻域搜索，寻找新的食物源，贪婪选择较优的食物源；

Step4 如果食物源的收益率没有通过预先确定的循环次数(limit)得到改善时，该处食物源被放弃，与之对应的雇佣蜂转化为侦察蜂。侦察蜂利用公式(5)产生新解。

Setp5 若迭代次数小于最大迭代次数，转至Step2；否则，输出最优解，算法结束。

2 仿真实验及结果分析

为测试本文算法的性能,选用表1给出的基准函数[8]进行测试。其中：f1～f3为单峰函数，用于检验算法收敛速度和精度；f4～f8为多峰函数，其局部最优解的个数会随着问题维数的增加呈指数增长，用于检验算法的整体寻优能力和算法跳脱局部最优值的能力。针对表1所列的8个函数，选取ABC算法、PSO算法、DE算法、EABC算法、ABC/best/1算法与本文算法分别在维数为50和100情况下独立运行50次，统计各算法的最优值、最差值、平均值和标准差，实验结果如表2～5所示。平均值反映了算法的求解精度，标准差反映了算法的稳定性。

表1 测试函数表达式、搜索空间和理论最优值

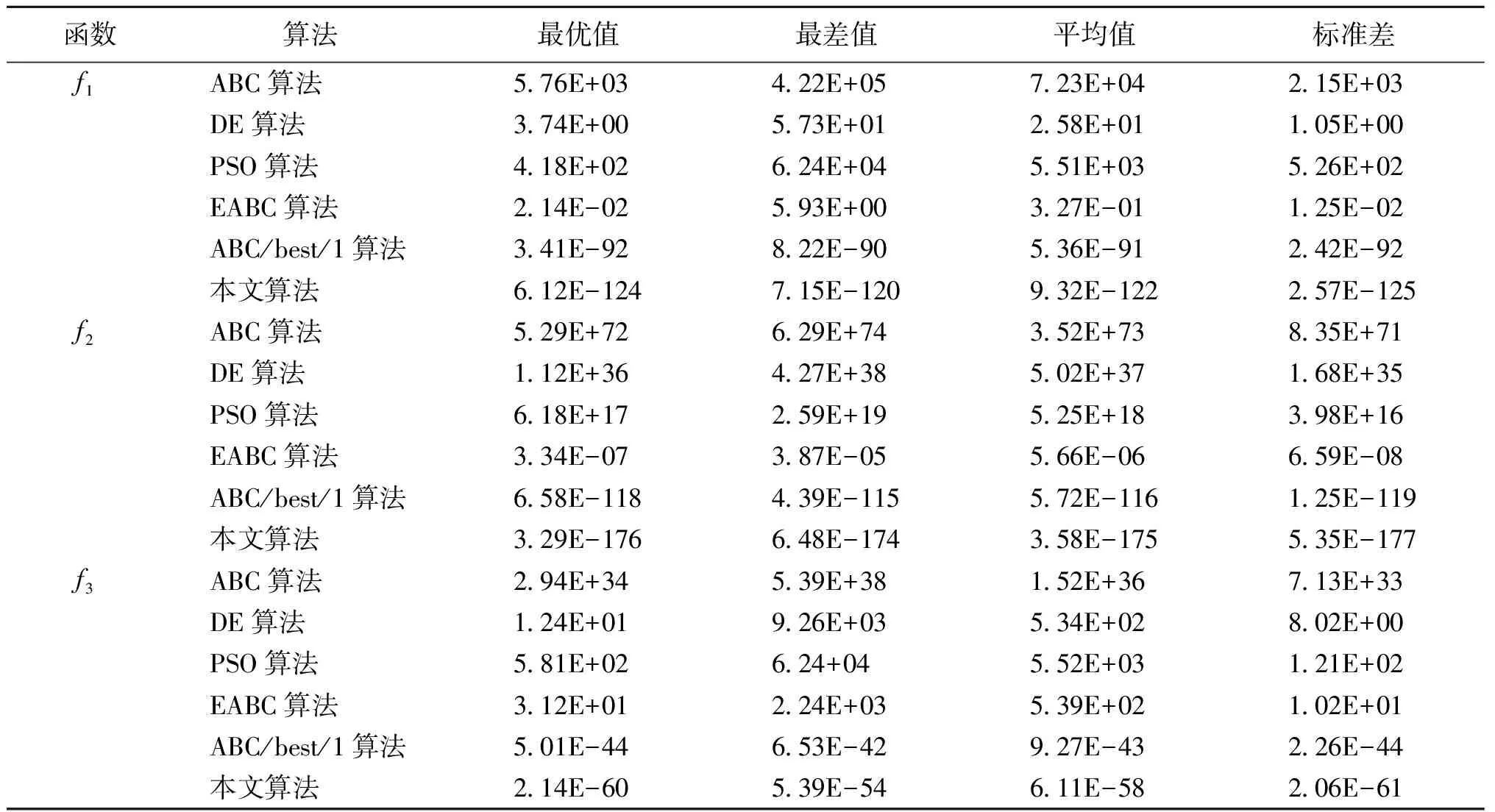
表2 各算法在50维情况下对单峰函数测试的实验结果

2.1 同维数不同算法的实验结果分析

单峰函数实验结果(表2)表明，ABC算法的稳定性差，收敛精度不高。实验结果可以看出，本文算法的最优值、最差值、平均值和标准差的精度与另外5种算法的精度相比都有明显提高。因此，说明在收敛速度和精度方面，本文算法优于其他算法，可以有效提高算法的局部搜索能力。多峰函数实验结果(表4)表明，ABC算法易陷入局部最优值，整体寻优能力差。f4和f8函数的实验结果显示，本文算法的最优值和最差值的精度与其他5种算法相比都有提高；f5、f6和f73个函数的实验结果显示，本文算法的最优值、最差值与另外5种算法相比都有明显提高。因此说明，算法在整体寻优能力及跳脱局部最优解方面，本文算法整体寻优能力较高，易于跳出局部最优解。

2.2 不同维数相同算法的实验结果分析

算法分别在50维和100维情况下，分别分析单峰函数实验结果(表2和表3)以及多峰函数实验结果(表4和表5)。数据表明：当维度是100时，f1、f2、f3、f5、f6和f76个函数的本文算法的寻优指标值优于另外5种算法；当函数维数降到50维时，本文算法的优势更为明显。

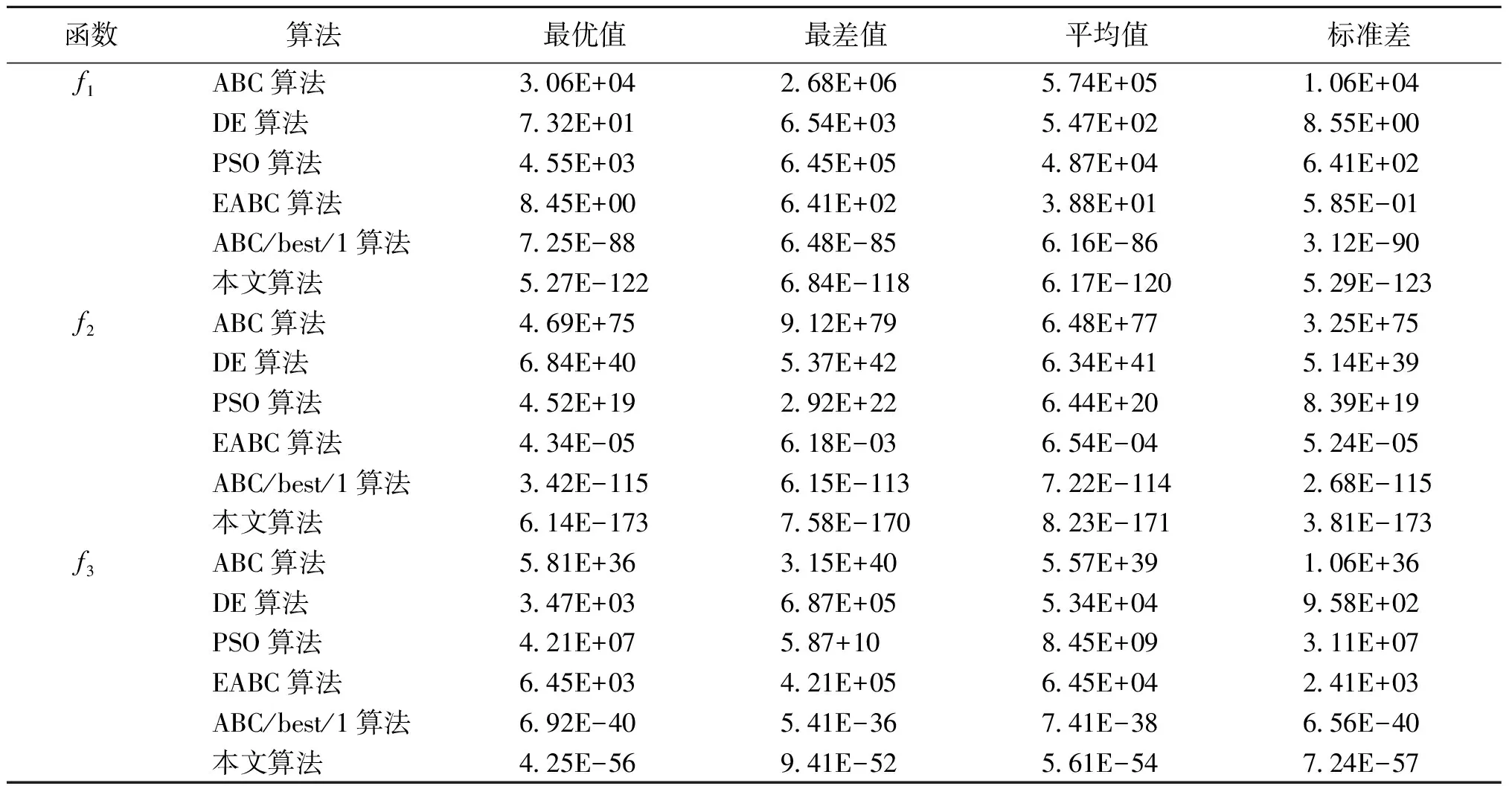
表3 各算法在100维情况下对单峰函数测试的实验结果

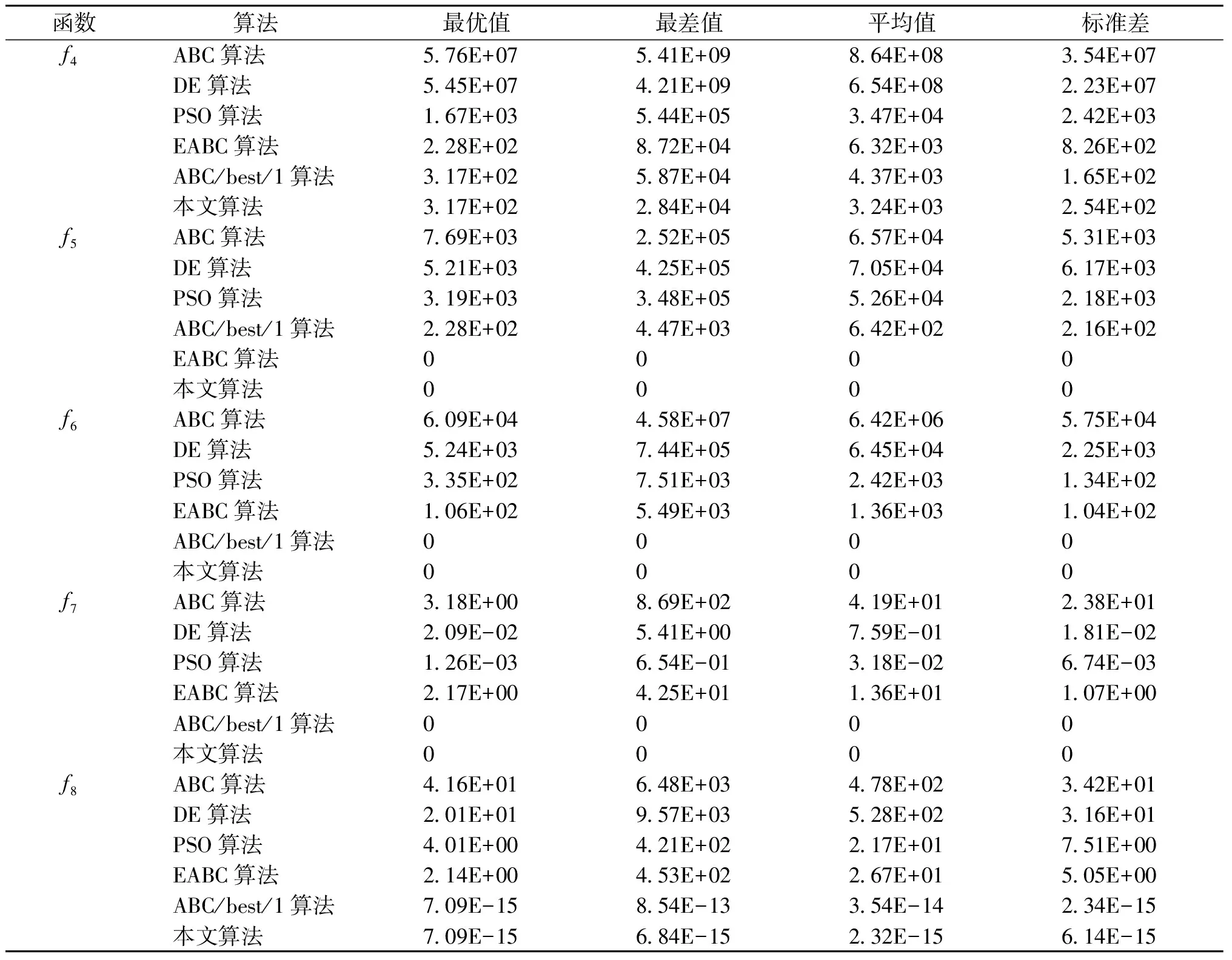
表4 各算法在50维情况下对多峰函数测试的实验结果

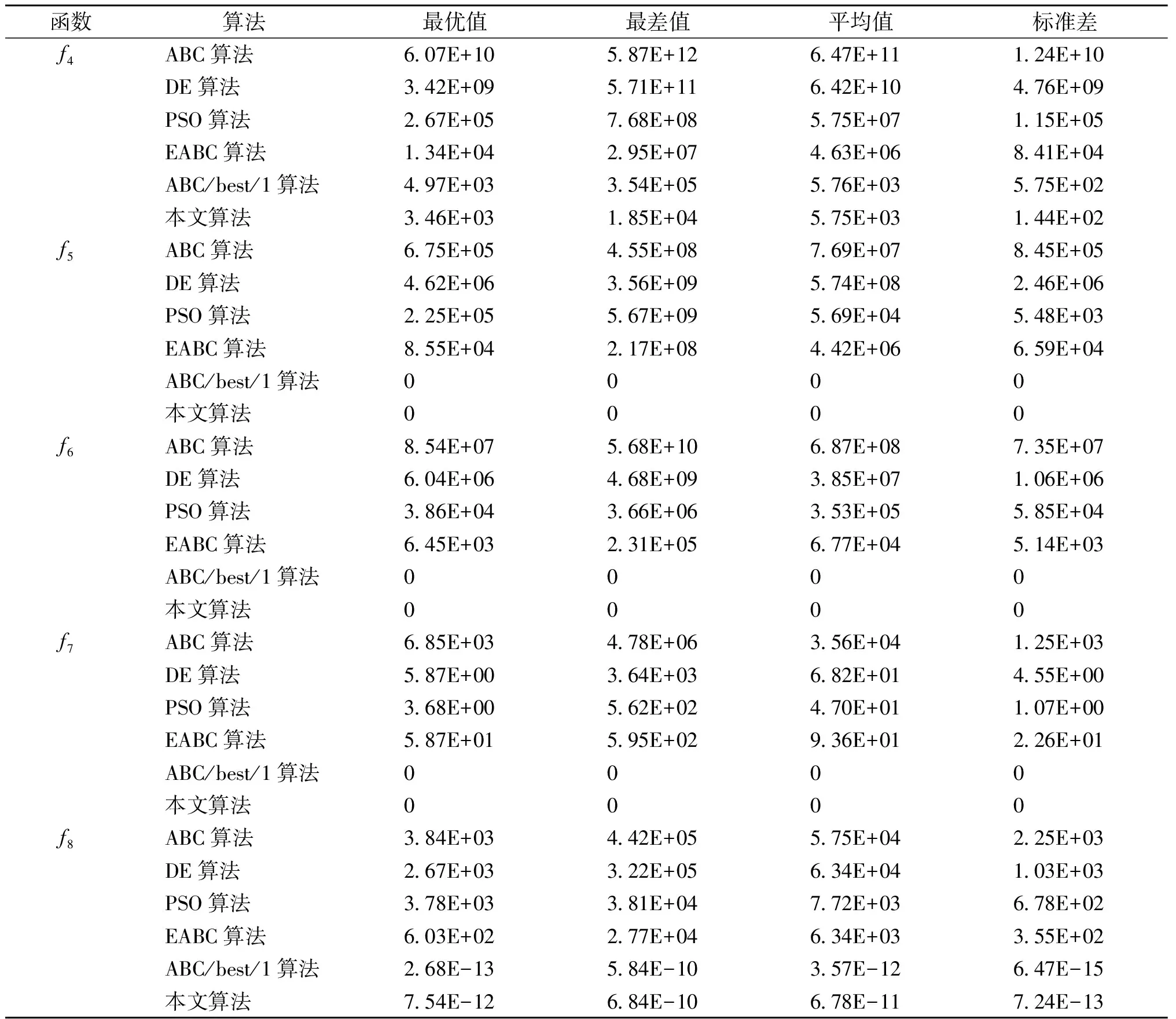
表5 各算法在100维情况下对多峰函数测试的实验结果

2.3 算法的性能测试

为了更直观地反映算法的性能, 针对表1所列的8个函数，分别采用ABC算法、DE算法、PSO算法、EABC算法、ABC/best/1算法与本文算法进行测试。图1展示了维数为50时，6种算法对测试函数的收敛曲线(为便于发现曲线间的差距，将各函数的适应度值取对数)。

图1 基准函数迭代曲线

根据图1(a)～(c)的单峰函数进化曲线可以得出，在收敛速度和求解精度方面，本文算法明显优于另外5种算法。故本文算法大幅度加快了算法的收敛速度，提高了求解精度。图1(d)为Rosenbrock函数的收敛曲线，该函数是一个病态的螺旋型函数，算法的初期阶段侧重于勘探能力，导致算法陷入局部最优解。随着迭代次数的增加，算法后期阶段侧重于开发能力，最优解的质量提高，对局部搜索行为指导作用明显。根据图1(e)～(g)的函数进化曲线可以得出，本文算法在收敛速度、精度和全局优化能力方面明显优于其他5种算法，本文算法收敛速度快且易于跳出局部最优解。图1(h)的函数进化曲线可以得出，在跳脱局部最优解方面，本文算法与其他5种算法相比都有提高。