计及IGBT暂态特性的光伏发电负载侧超高次谐波实验研究

岳家辉，张新燕，2，周 鹏，王 录，邢 琛，王 衡

（1.新疆大学 电气工程学院，新疆 乌鲁木齐 830047；2.可再生能源发电与并网技术教育部工程研究中心，新疆 乌鲁木齐 830047；3.国网新疆电力有限公司，新疆 乌鲁木齐 830047）

0 引言

光伏发电通过SPWM逆变器与电网系统相连，其电能质量受到研究人员的关注。电网系统中低次谐波污染已有了较为成熟的解决方案[1]～[3]，但由于SPWM逆变器在可再生能源网络各环节的广泛应用及开关频率的逐渐升高，所带来的超高次谐波污染问题日益突出[4]，[5]。

关于超高次谐波污染问题，已有相关人员进行了研究。文献[6]通过大量实验数据分析，初步确定了电网低压侧超谐波产生原因及传播特性。文献[7]，[8]对有关超谐波的测量标准做了初步探讨。文献[9]介绍了超谐波的产生原因与传播特性。文献[10]认为脉冲调制技术由于具有超高次、宽频域的谐波发射特性，符合超高次谐波的频率范围定义，可视为超高次谐波源。文献[11]指出规模化投入光伏逆变器，使电网中混杂着大量超高次谐波成分。在实际工作中，IGBT器件的开关延迟时间会因结温升高而改变，从而造成逆变电路输出电压谐波含量分布更为复杂。

针对上述问题，本文首先采用平均对称采样法，并考虑IGBT开关延迟时间的情况下，得到SPWM逆变电路输出电压谐波分布变化，证明了IGBT暂态特性不可忽略；然后，根据超高次谐波的宽频特性，提出一种基于K均值聚类与语谱图算法Spectrogram函数的谐波含量检测及显示方法，并给出算例进行验证；最后，搭建了IGBT测试系统与单相闭环光伏实验平台，根据本文所提方法，验证了IGBT开关延迟时间对光伏发电负载侧超高次电压谐波含量及分布的影响。

1 SPWM逆变电路输出电压谐波理论分析

1.1 忽略IGBT开关延迟时间

本节以三相SPWM逆变电路输出电压UA为主要研究对象，调制原理如图1所示。

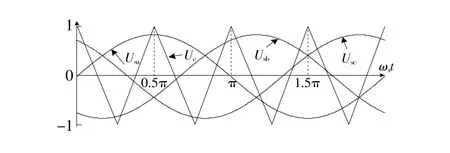
图1 SPWM逆变器调制原理Fig.1 The control diagram of SPWM inverter

其中:ω1为SPWM逆变电路中调制波频率；ωs为载波频率；M为调制比；M sin（ω1t）为调制波大小。平均对称规则采样法如图2所示。

图2 平均对称规则采样法局部放大图Fig.2 Average symmetric rule sampling local amplification

1.2 计及IGBT开关延迟时间

由于IGBT易受到寄生电感、寄生电容、内置驱动电阻之间相互耦合的影响，故其暂态特性不可忽视。由式（1）推导出:

由于式（8）中φ1含有sin（nπ/2），cos（nπ/2）分量，其值会随n奇偶性的改变而规律性变化，所以须要对谐波表达式AH′再次进行分解运算。进一步分析讨论可得:

当n为奇数时，有sin（nπ/2）=（-1）（n-1）/2，cos（nπ/2）=0，根据第一类贝塞尔函数，求得相电压UA谐波表达式为

令f1t=cos t∑·cos tΔ，f2t=sin t∑·sin tΔ，f3t=cos t∑·sin tΔ，f4t=sin t∑·cos tΔ，则在采用平均对称采样法并考虑IGBT暂态特性的情况下，三相SPWM逆变电路输出电压UA变化情况分别为

2 超高次谐波检测与显示方法分析

2.1 K均值聚类分析

IEC 61000-4-7标准提出了一种适用于高频域2×103～1.5×105Hz无间隙聚类测量方法，测量方法如图3所示。

图3 无间隙聚类测量示意图Fig.3 Schematic diagram of gapless clustering measurement

由图3可知，该方法对被测信号加矩形窗，然后对提取出来的被测信号进行DFT变换分析，最后根据Parseval能量定理得到高频域内谱线聚类中心频率，从而测得固定带宽的多组超高次谐波分量数据。

本文Parseval能量定理表达式为

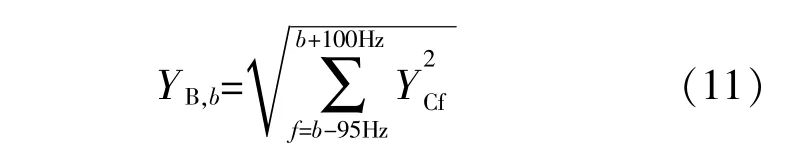
式中:YC，f为频谱分量有效值；b为中心点频率。

由于被测信号时域波形的能量同频域频谱的能量相等，即:

但是上述方法需要采集的数据量及计算量巨大，局限性明显。在权衡开销与检测精度后，基于上述理论，本文提出通过K均值聚类的超高次谐波检测方法，将高频域谐波幅值形成数据集，根据欧氏距离将频域内谐波幅值进行分簇，依据聚类中心点幅值的上下浮动来反映高次频域内谐波幅值的变化趋势，以减少繁重计算量。

2.2 算例1

为验证该谐波检测方法，本文给出电压测试信号，该信号由多个不同频率分量叠加而成，满足u=M sin（2πf·t）形式，f为分量频率大小，采样频率为4.4 kHz，采用4 400个点，为符合实际情况增添随机噪声，表达式为

0～2 s，该信号由8个频率分量叠加，包含50 Hz基波及19，20，21，38，39，41，42次超高次谐波，且各次谐波幅值大小同基波有显著差距。2 s后，谐波幅值微量增大，图4为该方法分析结果。

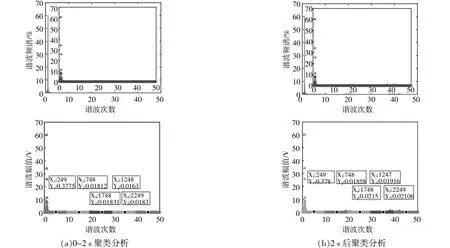
图4 K均值聚类结果Fig.4 K-means clustering result

由图4可知，该聚类谐波检测方法将频域内谐波幅值分为五簇，且每一簇的聚类中心点幅值随着信号中频率分量的增加而改变，基于模式识别范畴可得:10～30次谐波聚类中心点随时间的变化，其幅值分别由0.018 12升至0.018 58，0.0 16 3升至0.0 19 16；30～50次谐波聚类中心点随时间的变化，其幅值分别由0.0 18 31升至0.0 21 5，0.0 18 3升至0.0 21 06。由聚类结果可以看出，中心点幅值的浮动能够准确反映出在某一时间段内微量谐波的变化趋势。

2.3 语谱图算法的谐波显示方法

电网超高次谐波含量较低，且具有宽频特性，传统FFT难以直观、准确地观察微量超高次谐波的变化。本文将负载电压中超高次谐波等效为语音信号，使信号中谐波的微量变化无须削顶，而直观完整地显示出来。该方法改善了电力系统中谐波显示效果，克服FFT谐波分析的局限性，满足对电网中微量超高次谐波的观测要求。

语谱图算法能够描述信号中时间、频率与能量谱密度变化规律[13]，是一种用于时域信号分析与识别的重要方法。通过窗口函数w（n）对信号x（n）进行分析，其数学表达式为

式中:m为时间序列，与帧同步；w（n）为窗序列；N为一帧内采样点个数。

信号x（n）的离散时域傅里叶变换表达式为

式中:X（n，k）绝对值大小即为被分析信号x（n）的短时幅度预测。

某一时间的频谱能量密度函数W（n，k）为

通过频谱能量密度灰度级所得到二维图像就是语谱图。

2.4 算例2

该信号由多个不同频率分量叠加而成，除50 Hz基波外，包含19，21，37，43次超高次谐波，同基波相比幅值差距明显，且谐波幅值随时间发生微量变化；其余参数同算例1保持一致，其表达式为

将算例中谐波幅值变化曲线视为语音信号，可类比于时变信号进行处理，结果如图5所示。

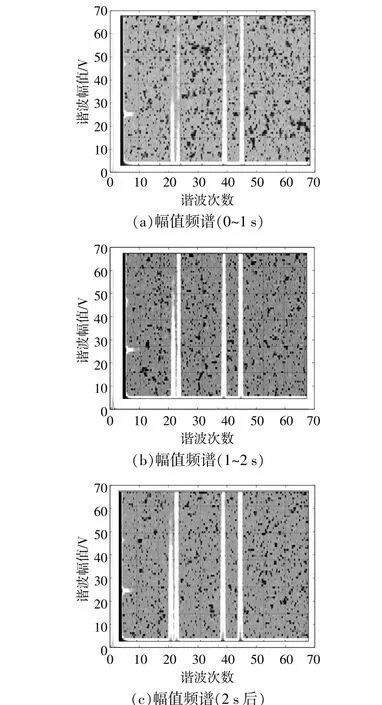
图5 基于语谱图算法的分析效果图Fig.5 Analysis supraharmonics based on key algorithms of spectrogram

由图5可知，语谱图算法的频谱图在19，21，37，43次频率处，色块亮度随时间变化而有较为明显的改变，更为直观的反映出微量变化过程，克服传统FFT的不足，能够满足对于系统中微量谐波的显示需求。

3 实验验证

3.1 开关延迟时间与结温关系

为明确IGBT开关延迟时间与结温关系，验证式（1），（7）理论的正确性，搭建IGBT开关特性离线测试系统进行实验分析[14]，对称规则采样。不同温度下的IGBT开关断VCE及栅极电压波形如图6所示。

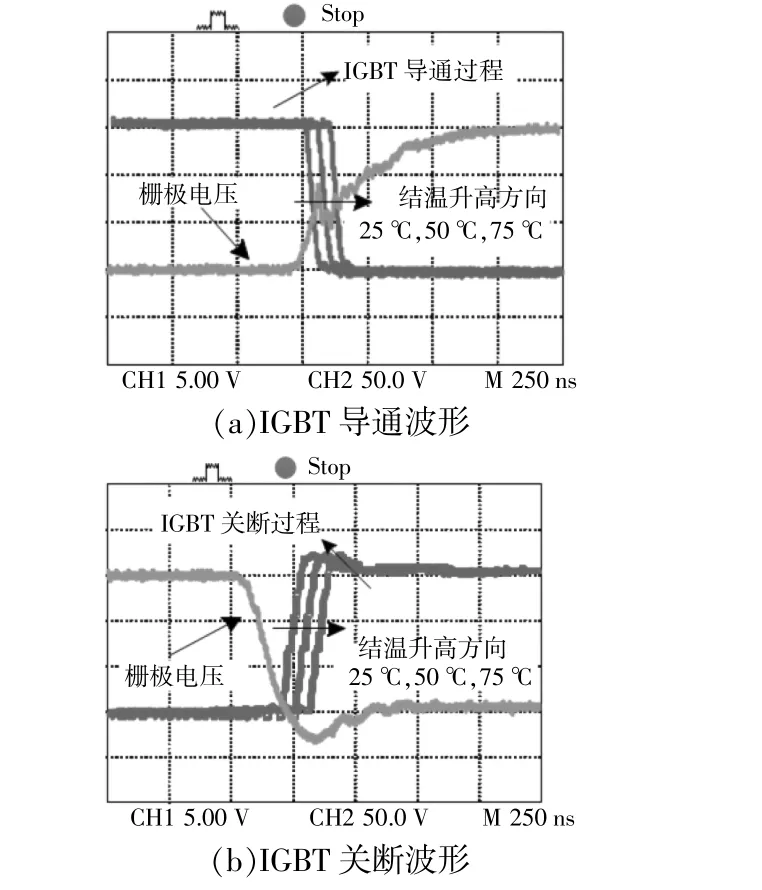
图6 不同温度下IGBT导通、关断波形Fig.6 IGBT switch on and off waveforms at different temperatures

本文IGBT选用FGL60N100，IGBT结至壳热阻RthJC为0.69 K/kW，结至外部环境热阻RthJA为25 K/kW，负载为60 W白炽灯、直流侧输出电压150 V，栅极-发射极峰值电压15V，室温为25℃，恒温加热台为ANSAI-100。该型号IGBT延迟开关时间与结温的拟合曲线如图7所示。

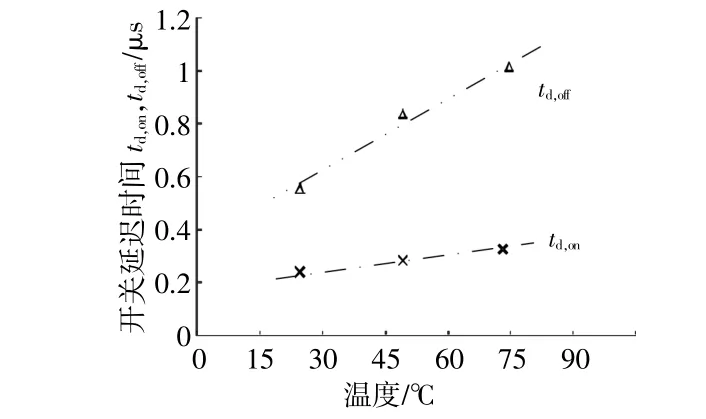
图7 开关延迟时间与结温拟合关系Fig.7 Fitting relationship between switch on/off time and temperature

由图（6），（7）可知，IGBT开关延迟时间随温度的升高而增大，呈现正系数关系，其暂态特性不容忽视。

3.2 光伏平台实验验证

为进一步探究IGBT暂态特性对负载侧的影响，并验证基于贝塞尔函数的式（10），（11）理论推导的正确性，根据低压配电网光伏发电网架结构，搭建单相闭环光伏发电实验平台，采用工频隔离型拓扑结构，如图8所示。

图8 单相闭环光伏发电实验平台Fig.8 Single phase closed-loop photovoltaic power generation experimental platform

驱动板中DC-AC逆变器驱动控制芯片为EG8011，IGBT栅极驱动芯片采用EG2126，逆变板中DC-AC逆变电路IGBT为FGL60N100，电源变压器变比为12/220 V，阻性负载，室温为25℃。恒温加热台为ANSAI-100，示波器型号为TDS-2024B，光伏板型号为BCT50-12。通过恒温加热台对逆变板整体升温，得到不同温度下负载电压波形，如图9所示。

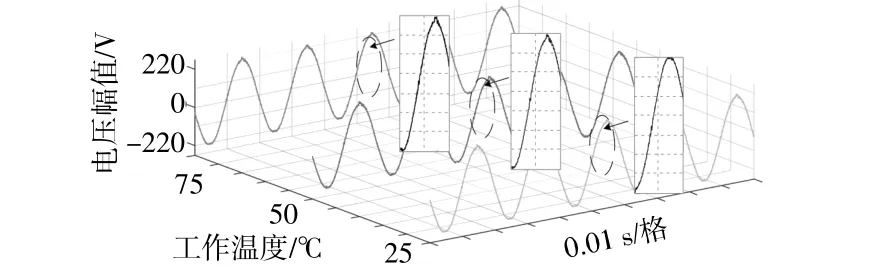
图9 不同温度下负载侧电压波形Fig.9 Voltage waveform at load under different temperature

由图9可以看出，电压波形存在一定程度的畸变，对其进行离散傅里叶变换，采用基于K均值聚类的超高次谐波检测方法，将高频域谐波幅值形成数据集，并对1.25×103～6.25×103Hz高频域内谐波幅值进行聚类分析，如图10所示。

图10 高频域谐波K均值聚类结果Fig.10 Clustering results of K-means in high frequency domain

根据欧氏距离将高频域谐波幅值数据集聚类成4簇，其高频域内聚类中心点幅值变化如表1所示。

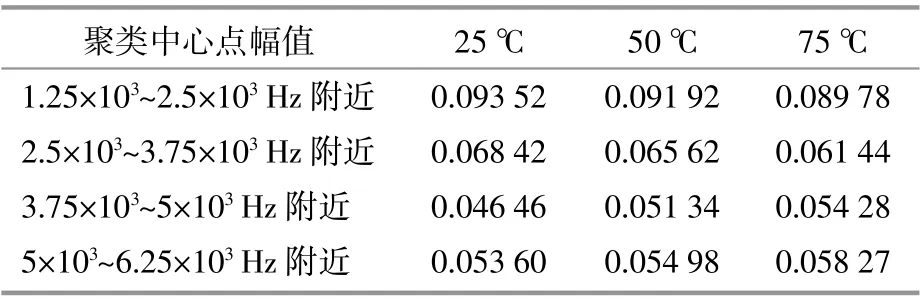
表1 不同温度下聚类中心点幅值大小Table 1 Amplitude change of center under different temperatures

由图10可以看出，在开关频率奇数倍附近，50次谐波及其边谐幅值，随着环境温度的升高而逐渐减少，即表1中25～50次谐波幅值聚类中心点幅值由0.093 52降至0.089 78；50～75次谐波幅值聚类中心点幅值由0.068 42降至0.061 44。在开关频率偶数倍附近，100次谐波及其边谐幅值，随着环境温度的升高而逐渐增多，即表1中75～100次谐波幅值聚类中心点幅值由0.046 46升至0.054 28，100～125次谐波幅值聚类中心点幅值由0.053 60升至0.058 27。同前文理论分析相同。

鉴于超高次谐波的宽频特性，且因幅值较低而频谱变化情况难以直观显示，采用基于语谱图算法的超高次谐波含量显示方法，如图11所示。

图11 高频域谐波含量显示效果Fig.11 The effect of Super harmonic content display

由图11可以看出，随着IGBT结温的升高，负载电压中开关频率奇数倍次附近谐波幅值存在一定程度变化:50次谐波处亮度逐渐降低，100次谐波处亮度逐渐增大，反映出开关频率奇数倍附近，谐波成分（nωs±kω1）含量减少；开关频率偶数倍附近，谐波成分（nωs±kω1）含量增多，电压总畸变率由2.00%升至2.61%，成分更为复杂，同文中理论分析一致。

4 结论

本文针对IGBT暂态特性对光伏负载侧电压中超高次谐波含量及分布情况影响的问题，提出基于K均值聚类与语谱图算法的超高次谐波综合分析方法。基于该分析方法，通过IGBT开关特性离线测试系统与单相闭环光伏发电实验平台对理论分析进行实验验证，得到以下结论:①IGBT开关延迟时间同温度成正系数关系；②文中所提出的基于K均值聚类超高次谐波检测方法，可以满足对系统中谐波变化趋势的检测，适用于现场测量，具有良好的工程应用价值；提出的基于语谱图算法的微量谐波显示方法有助于对新能源网络电能质量的研究分析；③随着IGBT结温的升高，负载侧所含超高次谐波的分布情况会发生一定变化:在开关频率奇数倍附近，nωs±kω1含量降低，其对应的超高次谐波及其边谐幅值下降；在开关频率偶数倍附近，nωs±kω1含量增多，其对应的超高次谐波及其边谐幅值增大，对光伏发电中超高次谐波抑制问题具有参考价值。