基于二阶数据分解算法和蝗虫优化混合核LSSVM的太阳辐照度预测模型研究

吴小涛，袁晓辉，袁艳斌，易凡茹，朱婧巍，吴育联

（1.黄冈师范学院 数学与统计学院，湖北 黄冈 438000；2.华中科技大学 土木与水利工程学院，湖北 武汉 430074；3.武汉理工大学 资源与环境工程学院，湖北 武汉 430070）

0 引言

影响光伏发电系统输出功率的主要因素为太阳辐照度。由于受温度、湿度和云层等因素的影响，太阳辐照度具有非线性，这导致光伏发电系统输出功率具有不稳定性、间歇性等特点。建立太阳辐照度预测模型并获得模拟数据，有利于电力调度部门根据模拟数据提前调整电能的存储和释放，实现光伏发电系统输出功率平滑输出，保持电网稳定工作，并且能够实现更多的光伏发电系统并网运行。

目前，太阳辐照度的预测模型主要包括基于太阳辐射传递的物理模型、基于卫星图像技术的预测模型和基于大数据驱动的统计预测模型。基于太阳辐射传递的物理模型建模过程复杂、抗干扰能力较差、鲁棒性不强；基于卫星图像技术的预测模型技术性较强、建设成本较高；基于大数据驱动的统计预测模型能够通过挖掘太阳辐照度及其影响因素的历史数据之间的内在规律，利用机器学习等算法建立太阳辐照度预测模型（以下简称为机器学习模型），与基于太阳辐射传递的物理模型、基于卫星图像技术的预测模型相比，机器学习模型具有投入成本较低、预测速度较快等优点，是目前主要的研究方向。

机器学习模型包括时间序列模型、神经网络模型和支持向量机模型等，其中，时间序列模型适用于太阳辐照度变化较小的情形，当太阳辐照度变化较大时，由于神经网络模型能解决非线性问题，其预测性能较好。神经网络模型的经验风险最小，但存在收敛速度慢、泛化能力弱且易陷入局部极小等问题；支持向量机模型的结构风险最小，具有很强的泛化能力，并且能够避免陷入局部极小等问题，其预测性能往往优于神经网络模型[1]～[3]。文献[4]对于同一组数据分别建立了自回归模型、神经网络模型和支持向量机模型，通过模拟计算发现，支持向量机模型的预测精度较高。最小二乘支持向量机（LSSVM）是一种改进的支持向量机，其求解速度优于支持向量机。文献[5]建立了计算太阳辐照度的LSSVM和人工神经网络预测模型，模拟结果表明，LSSVM模型的预测速度、精度均优于人工神经网络模型。LSSVM模型中的核函数和核函数中的参数决定着LSSVM模型的预测性能。

本文将泛化能力强、推广能力弱的高斯核函数和推广能力强、泛化能力弱的多项式核函数相结合，构建了混合核函数，并采用蝗虫优化算法（GOA）优化混合核函数中的参数，建立基于GOA优化混合核LSSVM的太阳辐照度预测模型，用来预测太阳辐照度 由于太阳辐照度时间序列不稳定，基于单一机器学习算法建立的太阳辐照度预测模型的预测精度较低。利用数据分解算法如小波分解（WD）算法、集合经验模态分解（EEMD）算法和变分模态分解（VMD）算法等对太阳辐照度时间序列进行分解，可以有效地降低太阳辐照度时间序列的不稳定性，因而，组合了机器学习和数据分解算法的太阳辐照度预测模型的预测精度高于基于单一机器学习算法的预测模型。

文献[6]～[8]分别建立了基于WD和神经网络、EEMD和神经网络、WD和支持向量机预测模型，模拟结果表明，组合预测模型的预测精度高于单一神经网络模型或支持向量机模型。不同的数据分解算法具有不同的特点，EEMD算法根据时间序列的极值分解太阳辐照度时间序列，虽然能有效分解出太阳辐照度时间序列的趋势分量和细节分量，但是其随机分量的频率高于原始太阳辐照度时间序列，预测误差会较大，从而降低了原始太阳辐照度时间序列的预测精度。VMD算法根据中心频率分解太阳辐照度时间序列，可将太阳辐照度时间序列有效地分解为多个不同、相对稳定的频率段序列。

本文根据EEMD算法和VMD算法的特点，设计了基于EEMD和VMD的二阶分解算法以分解太阳辐照度时间序列，具体的分解步骤:首先，采用EEMD算法分解原始太阳辐照度时间序列得到若干个分量；然后，利用VMD算法进一步分解频率最高的分量，得到若干个相对稳定的分量；接着，建立基于GOA优化的混合核LSSVM的太阳辐照度预测模型，对所有分量进行预测，累加所有分量的预测结果，即得到原始太阳辐照度时间序列的预测结果。本文提出的预测模型简称为EEMD-VMD-GOA-LSSVM模型。

1 理论与方法

1.1 EEMD算法和VMD算法

EEMD算法为Huang在经验模态分解（EMD）算法的基础上提出的改进数据分解算法，该算法解决了EMD算法分解过程中极易出现的模态混叠问题[9]。

VMD算法为Dragomiretskiy K在2014年提出的一种数据分解算法[10]。VMD算法中假设原始序列y（t）由K个带宽有限、频率不同的分量uk（t）（k=1，2，…，K）组成，从而将数据分解问题转化为变分问题，VMD算法包含变分模型的建立和求解2个步骤[11]。VMD算法在分解数据前须要确定模态个数K，若K小于真实值，会产生模态混叠现象；若K大于真实值，又会产生过分解现象；若K等于真实值，分解得到的残差与原始序列的相关系数的绝对值较小，因此，本文提出设定某个阈值，即设定K的初始值为2，当分解得到的残差与原始序列的相关系数不小于阈值时，令K=K+1，直到分解得到的残差与原始序列的相关系数小于阈值时，停止分解，此时K的值即为最优的模态个数。

1.2 GOA

GOA为Shahrzad Saremi在2017年提出的一种智能优化算法[12]。在蝗虫集群过程中，任意2个蝗虫个体之间有引力和斥力2种社会行为，蝗虫个体之间距离越近，斥力越大，引力越小；距离越远，引力越大，斥力越小。GOA模拟的斥力能够实现全局探索，模拟的引力能够实现局部开发。所有蝗虫个体之间共享位置信息，通过不断缩小搜索空间获得最优解。

令第i，j个蝗虫之间的距离为dij。dij的计算式为

式中:qi为第i个蝗虫的位置；qj为第j个蝗虫的位置。

令第i，j个蝗虫之间的社会行为强度为s（dij）。s（dij）的计算式为

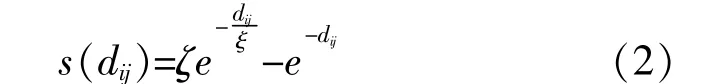
式中:ζ，ξ均为常数，ζ=0.5，ξ=1.5。

令第i个蝗虫个体的社会行为为Si。Si的计算式为

GOA的寻优步骤如下。

①将含有n0个蝗虫的群体初始化为一群随机粒子（随机解），令Yi（i=1，2，…，n0）为第i个粒子的当前位置，根据适应度函数计算每个粒子的适应度值，得到所有粒子当前的最优位置T*。

②每个粒子利用式（5）更新后的位置Yi。Yi的计算式为

式中:ub，lb分别为搜索空间的上界和下界；c为平衡算法全局和局部搜索能力的线性递减系数。

c的计算式为

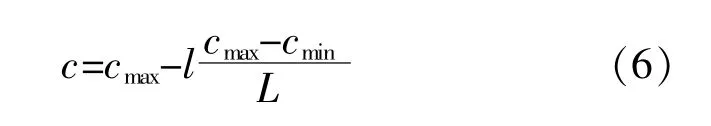
式中:L，l分别为最大迭代次数和当前迭代数；cmin，cmax分别为c的最小值、最大值，取cmin=10-5，cmax=1。

③迭代数l=l+1，并利用式（6）更新c的值。

④计算更新位置后的粒子的适应度值及最优位置，判断最优位置是否优于T*。若优于则用其替代T*，否则保持T*不变。在更新位置时，如果粒子的位置小于搜索空间的下界lb，则将粒子的位置置于lb；如果粒子的位置大于搜索空间的上界ub，则将粒子的位置置于ub。

⑤根据迭代终止条件（最大迭代次数或误差值）判断是否结束寻优，若结束则返回T*，否则返回③继续进行迭代。

在GOA寻优时，c的取值对算法性能的影响较大。在迭代初期，智能优化算法往往须要变化幅度较大的c值来实现全局搜索，确定最优解的大致范围；在后期须要变化幅度较小的c值实现局部精细开发确定最优解。显然线性递减的c不能满足上述要求，为此本文提出基于非线性的逆不完全伽马函数的c值调整方法，即将式（6）表达式更换为

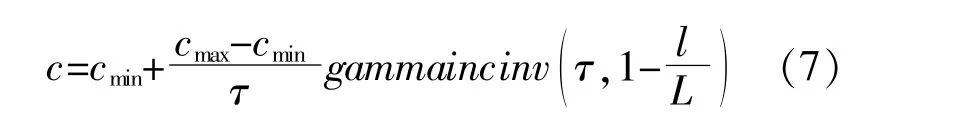
式中:gammaincinv（τ，1-l/L）为逆不完全伽马函数在Matlab中的调用函数，返回在τ和1-l/L处计算的下不完全伽马函数的逆函数，其中τ为随机参数，取0.2。

与式（6）相比，式（7）在迭代初期具有变化幅度较大的c，利于GOA实现全局探索；在迭代后期，具有变化幅度较小的c，利于GOA实现局部精细开发，从而使GOA具有更好地平衡全局探索和局部精细开发的能力。

1.3 LSSVM

LSSVM采用映射将非线性问题转化为高维特征空间中的线性问题[13]。假设样本集为{（xi，yi）|i=1，2，3，…，N}，其中:xi为多维的输入样本数据；yi为与xi对应的一维输出样本数据；N为样本个数。

构造线性回归函数为

式中:w为高维特征空间中权系数列向量；b为偏差，b∈R；φ（x）为非线性映射，φ（x）=[φ（x1），φ（x2），…，φ（xN）]T。

w和b通过最小化结构风险函数R来确定。R的计算式为

式中:εi为误差；γ为惩罚系数，γ＞0。

利用拉格朗日乘数法求解式（9）。拉格朗日函数L（w，b，ε，μ）的计算式为

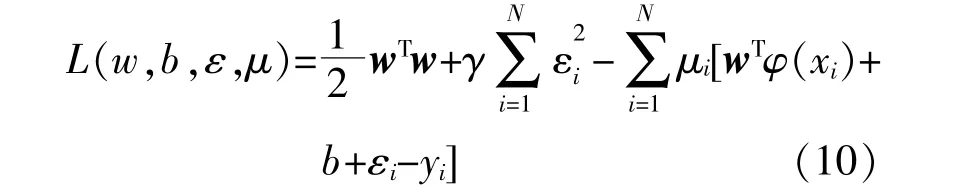
式中:μi为拉格朗日乘子。

通过KKT条件，将式（10）转化为求解线性方程组问题，转化结果见式（11）。

本文选择泛化能力强、推广能力弱的高斯核函数和推广能力强、泛化能力弱的多项式核函数构建混合核函数。

式中:Ker（xi，xj）为核函数，其中i，j=1，2，…，N。

混合核函数的表达式为

式中:β为权值，0≤β≤1；σ为高斯核函数的核宽，σ＞0；r，p为多项式核函数中的参数，r＞0，p为正整数。

求解式（11）得到μi和b，从而得到LSSVM的最优回归函数表达式为

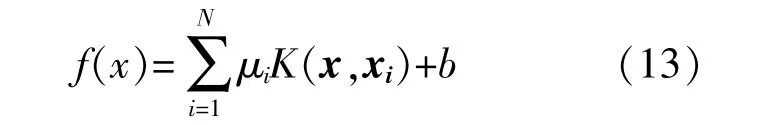
根据回归函数式（13）即可对未知点进行预测。

混合核函数中的参数β，σ，r，p会直接影响LSSVM模型的预测性能，本文采用GOA对上述参数进行优化，从而建立最优的混合核LSSVM的太阳辐照度预测模型。

2 EEMD-VMD-GOA-LSSVM预测模型

为了降低原始太阳辐照度时间序列的不稳定性，本文利用EEMD-VMD二阶分解算法对原始太阳辐照度时间序列进行分解，即先利用EEMD算法分解原始太阳辐照度时间序列，得到n个分量IMF1，IMF2，…，IMFn，然后利用VMD算法对频率最高的分量（本文假设IMF1的频率最高）进行分解，得到K个分量IMF11，IMF12，…，IMF1K，则原始太阳辐照度时间序列被分解成n-1+K个分量。

建立基于GOA优化的混合核LSSVM的太阳辐照度预测模型对n-1+K个分量进行预测，累加所有预测结果即可得到原始太阳辐照度时间序列的预测结果。具体预测步骤如下。

①利用EEMD-VMD二阶分解算法分解原始太阳辐照度时间序列，得到若干个分量。

②对每个分量，选择最后若干个数据作为测试数据集，其余数据作为训练数据集。

③建立混合核LSSVM的太阳辐照度初始预测模型，在训练数据集中利用GOA对混合核函数的参数进行优化，利用优化后的混合核LSSVM的太阳辐照度预测模型对每个分量的测试数据集进行预测，得到每个分量的预测结果。

④将③中每个分量的预测结果进行叠加，得到原始太阳辐照度时间序列的预测值。

EEMD-VMD二阶分解算法流程图见图1。

图1 EEMD-VMD二阶分解算法流程图Fig.1 Two-stage decomposition algorithm flow diagramwith EEMD-VMD

3 实验分析

3.1 数据来源及数据整理

由于太阳辐照度具有较强的季节周期性和昼夜周期性，本文选取某个太阳能监控平台收集的夏季每日8:00-16:00各整点时刻的太阳辐照度和部分气象数据（温度、相对湿度和气压），共810组数据。

太阳辐照度随时间的变化情况如图2所示。

图2 太阳辐照度随时间的变化情况Fig.2 Variation of solar irradiance with time

由图2可知，太阳辐照度时间序列整体上表现出非线性的特点，这是由于太阳辐照度受到温度、相对湿度和气压等因素的影响。

温度、相对湿度和气压随时间的变化情况如图3所示。

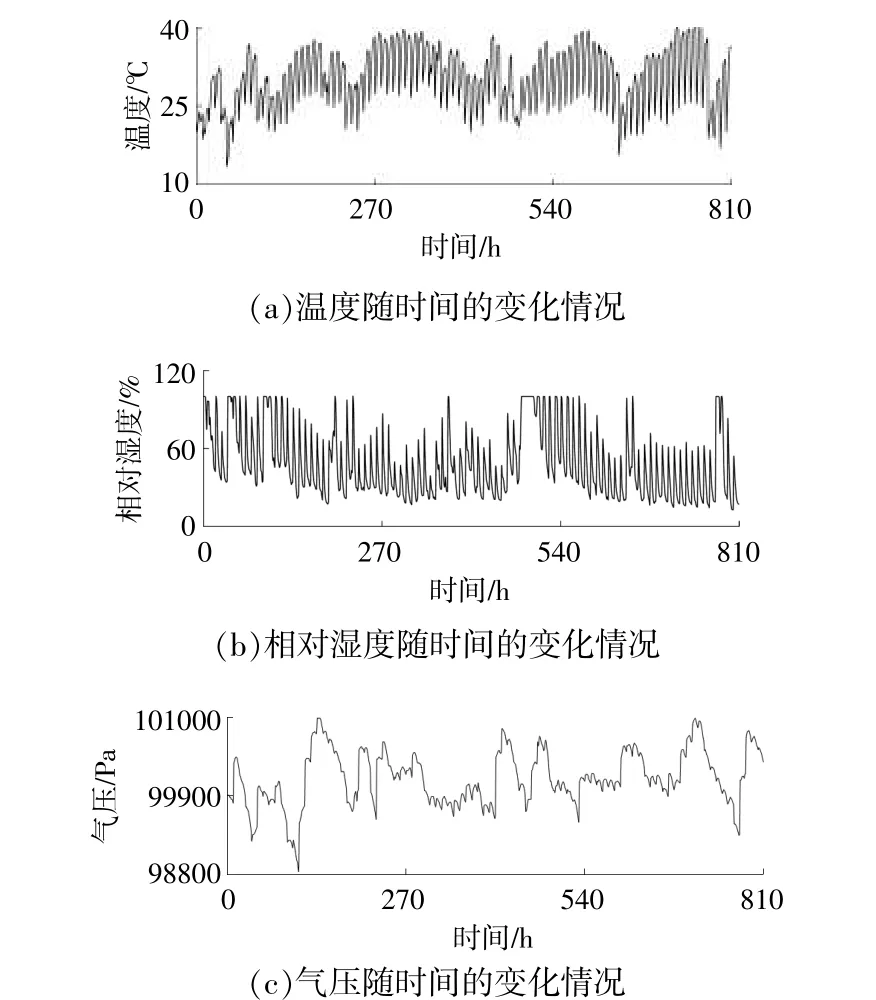
图3 温度、相对湿度和气压随时间的变化情况Fig.3 Variation of temperature，relative humidity and air pressure with time

由图2、图3（a）可知，温度随时间的变化情况与太阳辐照度随时间的变化情况基本一致，即当温度较低时，太阳辐照度较小；当温度较高时，太阳辐照度较大。由图2、图3（b）可知，相对湿度随时间的变化情况与太阳辐照度随时间的变化情况基本相反。由图2、图3（c）可知，气压随时间的变化情况与太阳辐照度随时间的变化情况无关。进一步分析发现，对原始太阳辐照度时间序列进行异常值和归一化处理后，利用皮尔逊相关系数计算太阳辐照度与温度、相对湿度和气压的相关系数，得到相关系数分别为0.7，-0.7，0.1，由此可知，太阳辐照度与温度呈中度正相关，与相对湿度呈中度负相关，与气压不相关。因此，本文中的气象因素只须考虑温度和相对湿度，在建立混合核LSSVM的太阳辐照度预测模型时，将温度和相对湿度作为输入，以提高模型的预测精度。

3.2 EEMD-VMD二阶分解算法

利用EEMD算法对整理后的太阳辐照度时间序列进行分解，其中，噪声方差Nstd取0.01，噪声组数NE取100，得到9个分量IMF1～IMF9。利用EEMD算法分解原始太阳辐照度时间序列的结果如图4所示。

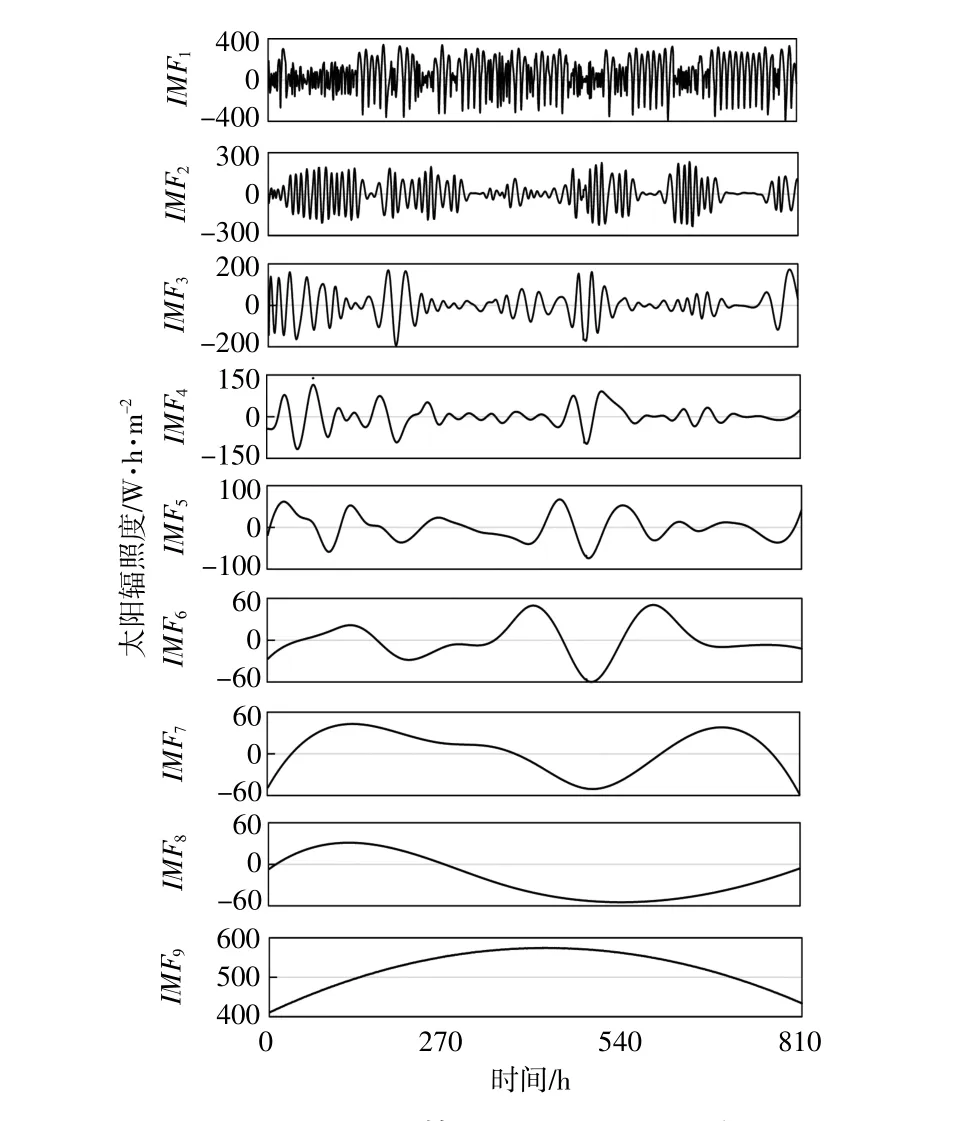
图4利用EEMD算法分解原始太阳辐照度时间序列的结果Fig.4 Decomposition results of original solar irradiance time series using EEMD algorithm

由图4可知:IMF9反映了原始太阳辐照度时间序列的整体变化趋势，变化频率最小；IMF2～IMF8反映了原始太阳辐照度时间序列的细节变化情况，变化频率虽然较大，但小于原始序列；IMF1的变化频率最高。

利用VMD算法对IMF1进一步分解，其中，带宽限制alpha取2 000，噪声容限tau取1。对于模态个数K，按照前文提出的方法，设定相关系数的阈值为0.005，计算得到K=2，3，4，5，6，7时，IMF1与分解残差的相关系数分别为-0.01，0.307，0.1 99，0.0 02，0.0 01，0.0 01。因此，取K=5，此时残差与原始太阳辐照度时间序列的相关系数仅为0.0 02。当K取6，7或更大时，残差与原始太阳辐照度时间序列的相关系数变化不大，再分解会产生过分解现象。利用VMD算法对IMF1进行分解得到5个分量和1个残差分量，记为IMF11～IMF16。

综上所述，利用EEMD-VMD二阶分解算法分解原始太阳辐照度时间序列可得到14个分量，分别为IMF11～IMF16，IMF2～IMF9。利用VMD算法分解IMF1得到的结果如图5所示。

图5 利用VMD算法分解IMF 1得到的结果Fig.5 Decomposition result of IMF1 using VMD algorithm

3.3 LSSVM预测模型的输入和输出

本文拟对未来2 d中8:00-16:00各整点时刻的太阳辐照度进行短期预测。对于利用EEMDVMD二阶分解算法分解得到的各分量，选择最后18个数据（793～810 h）作为测试数据，前792个数据作为训练数据，并建立基于GOA优化的混合核LSSVM的太阳辐照度预测模型，该模型的输入根据太阳辐照度时间序列的偏自相关系数的截尾特性来确定。具体地，如果太阳辐照度时间序列为J阶截尾，那么将t时刻的太阳辐照度作为输出，其对应的t-1，t-2，……，t-J这J个时刻的太阳辐照度、温度和相对湿度作为输入。对原始太阳辐照度时间序列建立基于GOA优化的混合核LSSVM的太阳辐照度预测模型，通过对比输入中是否包含温度和相对湿度的实验结果发现，包含温度和相对湿度的预测结果的平均绝对误差为13.0%，而不包含时预测结果的平均绝对误差为16.5%，因此，输入变量中包含温度和相对湿度时，预测精度更高。

3.4 预测模型评价指标

本文采用决定系数R2、平均绝对误差MAPE、平均相对误差MRE和均方根误差RMSE这4个指标对EEMD-VMD-GOA-LSSVM模型进行评价分析。其中:R2用来检验模型的拟合度，R2值越大，说明模型的拟合程度越好；MAPE，MRE和RMSE用来检验模型的精度，它们的值越小，说明模型的预测精度越高。R2，MAPE，MRE和RMSE的计算式分别为

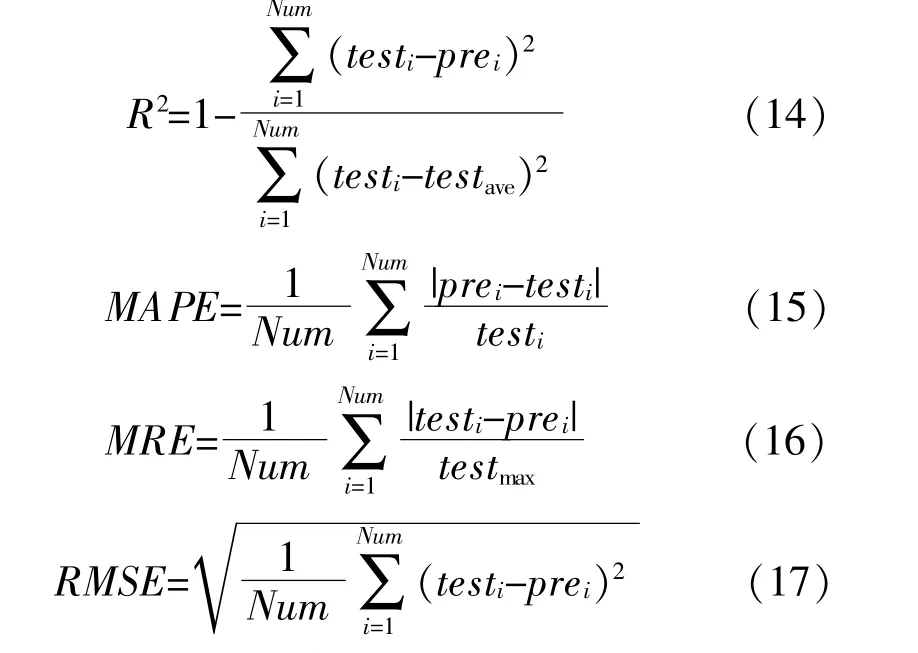
式中:testi，prei分别为i时刻太阳辐照度的实测值、预测值；Num为预测样本总数；testmax，testave分别为测试样本中太阳辐照度实测值的最大值和平均值。

4 实验结果分析

为了检验EEMD-VMD-GOA-LSSVM模型的预测性能，本文分别建立了ARIMA（p，d，q）模型、GOA-LSSVM模型、GOA-BP神经网络模型和EEMD-GOA-LSSVM模型用于比较。ARIMA（p，d，q）模型中p，d，q分别为自回归（AR）的项数，差分（I）的系数，移动平均（MA）的项数。在ARIMA（p，d，q）模型中，通过反复验证得知，当p=3，d=1，q=3时，该模型的预测精度最高；在GOA-LSSVM模型中，核函数采用本文提出的混合核函数，GOA用来优化核参数，适应度函数选择平均绝对误差函数，初始蝗虫群体个数取10，最大迭代次数为10；在GOA-BP神经网络模型中，GOA用来优化BP，实验得出隐含层、输出层中神经元的个数分别为22，12时，该模型的预测精度最高。在EEMD-GOA-LSSVM模型中，利用EEMD算法分解原始太阳辐照度时间序列得到9个分量，即IMF1～IMF9，建立基于GOA优化的混合核LSSVM预测模型，对9个分量进行预测，再累加这9个分量的预测值，得到原始太阳辐照度时间序列的预测结果。

5种预测模型的预测曲线图如图6所示。由图可知，5种预测模型中，ARIMA（p，d，q）模型的预测精度最差，其次为EEMD-GOA-LSSVM模型，GOA-LSSVM和GOA-BP模型的预测精度稍好，其预测曲线整体上追随实测值曲线波动，但在某些点的误差较大，EEMD-VMD-OA-LSSVM模型的预测精度最高，其预测曲线与实测值曲线几乎重合。

图6 5种预测模型的预测曲线图Fig.6 Prediction curves of five forecasting models

为了便于比较，本文将801～803 h，5种预测模型的预测曲线和实测值曲线局部放大，具体如图7所示。

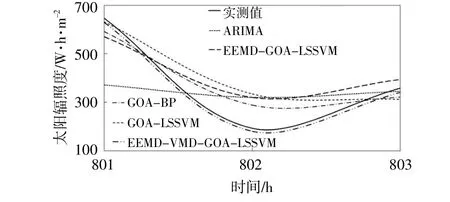
图7 5种预测模型的预测曲线局部放大图Fig.7 Local enlarged map of prediction curve of five prediction models

由图7可知，在801，802 h和803 h这3个时刻，EEMD-VMD-GOA-LSSVM模型的预测值均小于实测值，但它们的差值较小，而其余4种模型的预测值与实测值之间的差值较大，在802 h时最大。

5种预测模型的误差值如表1所示。

表1 5种预测模型的误差值Table 1 Error values of five prediction models

由表1可知，EEMD-VMD-GOA-LSSVM模型的MAPE为2.3%，MRE为1.3%，这说明该模型的预测值与实测值间的误差非常小，预测精度非常高，其余4种预测模型的MAPE均大于10%，MRE均大于5%，这说明它们的预测值与实测值间的误差大，预测精度较低；EEMD-VMDGOA-LSSVM模型的RMSE为12.2，远小于其余4种模型，这说明EEMD-VMD-GOA-LSSVM模型的预测值与实测值的离散程度更小；在模型拟合度方面，EEMD-VMD-GOA-LSSVM模型的R2值为0.99，而其余4种模型的R2值均小于0.9，这说明EEMD-VMD-GOA-LSSVM模型能更好地反映原始太阳辐照度时间序列的变化情况。综合上述预测曲线图和误差的分析可知，EEMD-VMDGOA-LSSVM模型具有较好的预测性能。

5 结论

本文针对太阳辐照度时间序列不稳定的特点，提出了一种基于EEMD-VMD二阶数据分解算法和GOA优化混合核LSSVM的太阳辐照度预测模型，并利用该模型对太阳辐照度进行了预测，得到如下结论。

①利用EEMD-VMD二阶分解算法得到的分量不仅能反映原始太阳辐照度时间序列的变化情况，而且较原始太阳辐照度时间序列更加稳定。没有采用数据分解算法的GOA-BP模型、ARIMA模型和GOA-LSSVM模型的MAPE均高于13%，而采用EEMD-VMD二阶分解算法的EEMDVMD-GOA-LSSVM模型的MAPE仅为2.3%，这说明组合了EEMD-VMD二阶分解算法的太阳辐照度预测模型比未使用数据分解算法的太阳辐照度预测模型的预测精度更高。

②针对VMD算法中模态个数K难以确定的问题，本文提出了基于原始太阳辐照度时间序列和分解残差的相关系数来确定的方法。

③与ARIMA模型、GOA-LSSVM模型、GOABP神经网络模型和EEMD-GOA-LSSVM模型相比，EEMD-VMD-GOA-LSSVM模型的预测精度更高，能有效地反映太阳辐照度的变化规律。