基于模糊控制的自动驾驶汽车爆胎控制

陈齐平，王 亮，罗玉峰，谢加超，刘 权

（华东交通大学 载运工具与装备教育部重点实验室，南昌 330013）

0 引言

在人工智能的大背景下，自动驾驶汽车日益突出，但其出行的安全和高效得到广泛的关注。但自动驾驶汽车行驶过程中轮胎也会出现爆胎工况，其径向、纵向和侧向动力学特性都发生突变[1]，容易导致车辆驶入其它车道甚至翻车等事故。根据美国统计数据可知[2]，由于爆胎导致的车祸达到近9万起，引起400多人死亡，约1000人受伤。而当车辆高速行驶时，轮胎的机械损伤和热损伤积累易导致车辆发生爆胎，因此，研究基于模糊控制的自动驾驶汽车爆胎控制有着重要意义。

天津大学胡超芳[3]通过模型预测控制的方法对自动驾驶汽车爆胎控制，提高了系统响应速度和控制精度，车辆非线性运动位姿在转化成线性过程中有少量误差。广西工学院张彦会[4]采用模糊控制算法，能有效控制了爆胎车辆跑偏，但较少对爆胎车辆的横向位移进行分析。胎压检测是预防爆胎的一种重要手段[5]，但自动驾驶汽车中视觉传感器CCD、激光传感器易受环境影响，车轮容易驶入凹凸路面导致车辆爆胎，很难从根本上解决问题。基于输入状态鲁棒性控制的爆胎研究提高车辆爆胎稳定性控制，研究过程中较少考虑到最优输入[6]。利用差动制动方法，通过线性二次型调节器LQR有效地控制车辆爆胎后操纵稳定性，但需要借助实时特性确定加权矩阵[7]。利用增益可变的PID控制器能有效地控制爆胎轨迹[8]，出现较少偏差后调整到原路径，横摆角速度数值是决定乘客乘坐车辆舒适性重要因素之一，从实验结果可知，横摆角速度波动较大。

本文针对自动驾驶汽车爆胎控制存在的不足，首先建立线性二自由度车辆模型，自动驾驶汽车因爆胎导致轮胎参数发生剧烈变化，为此，根据附着椭圆理论，本文根据点刹和微调前轮转向角的方式设计了模糊控制器，最后通过Carsim与Simulink联合仿真，结果表明基于模糊控制的自动驾驶汽车爆胎控制方法能有效控制爆胎，提高车辆安全性和稳定性。

1 爆胎后偏航原因分析

轮胎发生爆胎后，其参数发生显著变化，滚动阻力系数增加20多倍，侧偏刚度下降原来0.28倍左右[9]，爆胎引起的参数变化，如图1所示。

图1 爆胎引起的参数变化

由图1(b)可知，左前轮爆胎其滚动阻抗系数瞬间增大，右前轮保持不变，因地面对左右轮滚动阻力不同使自动驾驶汽车产生逆时针转矩，从而导致汽车向左发生偏航。在无控制的工况下，自动驾驶汽车通过传感器、视觉算法等感知位姿，获得电信号通过CAN总线传输到自动驾驶汽车VCU系统，系统形成执行信号通过CAN总线给转向电机，使自动驾驶汽车向右行驶。而由图1(a)可知，爆胎后轮胎侧偏刚度下降，导致地面提供侧向力减小，不足以使车辆右转，因此自动驾驶汽车极易制动跑偏和侧滑，甚至发生翻车等事故。

2 线性二自由度车辆模型

为简化模型复杂程度，通过等效的自行车模型的方法，建立线性二自由度车辆模型，如图2所示。其中Pxy是车体坐标系。

图2 线性二自由度车辆模型

由图2可知，二自由度自动驾驶汽车的动态方程如下：

其中，m表示汽车的质量，Jz表示转动惯量，δ表示前轮转向角，r表示横摆角，β表示质心侧偏角，a表示车辆质心到前轴的距离。b表示质心到后轴距离。V表示质心速度，Ff和Fr分别表示地面作用于前、后轮胎的侧偏力。

其中，βf表示前轮侧偏角，βr表示后轮侧偏角，Kf表示前轮侧偏刚度，Kr表示后轮侧偏刚度。将式(3)、式(4)代入式(1)、式(2)得：

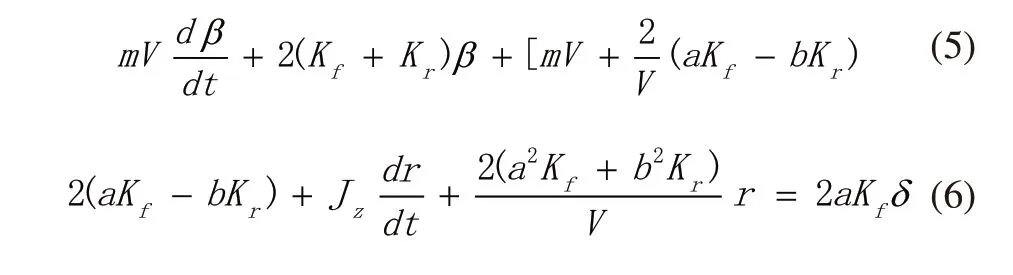
由式(5)、式(6)可建立线性二自由度车辆Simulink模型，通过车辆动力学仿真软件Carsim内部求解出整车转向角δ和质心车速V，求解量输入到自动驾驶汽车线性二自由度车辆模型中，输出质心侧偏角β和横摆角速度r。

3 控制器设计

3.1 附着椭圆理论

车辆因爆胎导致轮胎参数改变发生偏航，因此，车辆弯道行驶受到地面对轮胎产生侧向力。车辆处于制动工况，制动力和侧向力平方和最大值为常数；车辆处于驱动工况，驱动力和侧向力平方和最大值也为常数[10]。

其中，acmax表示最大附着加速度，为常数，ay表示侧向加速度，axb表示制动时纵向加速度，axf表示驱动时纵向加速度，由牛顿第二运动定律近似可知：

其中，Fcmax表示最大附着力，为常数，Fy表示侧向力，Fb表示制动时纵向力，Fa表示驱动时纵向力。自动驾驶汽车超过最大附着力，轮胎就会出现打滑等危险工况。力可以通过几何关系表示，即附着椭圆，如图3所示。

图3 附着椭圆

汽车发生爆胎后导致轮胎参数改变，轮胎力学性能下降，因此地面作用于轮胎的纵向力和侧向力平方和减小，即最大附着力减小。根据附着椭圆理论，本文提出通过点刹与微调前轮转向角的方式，用于控制爆胎后自动驾驶汽车稳定性，点刹与微调前轮转向角分别均降低爆胎自动驾驶汽车受到的地面纵向力和侧向力，因此使纵向力、侧向力和最大附着力仍满足附着椭圆理论，可充分利用地面附着系数使自动驾驶汽车安全制动和稳定性。

3.2 模糊控制

通过分析，采用点刹与微调前轮转向角的方式不需要建立准确的数学模型，通过模糊规则可设计模糊控制器[11]，但须结合合理的经验。当爆胎车辆质心侧偏角较小时，以横摆角速度的控制为主，当爆胎车辆质心侧偏角较大时，以质心侧偏角控制为主[12]。车辆因爆胎导致偏航，则车速是影响车辆横摆角速度大小重要因素之一，因此质心侧偏角和车速是模糊控制器的输入，根据附着椭圆理论确定模糊控制器输出为轮缸制动压力和转向角。MATLAB中开发出多达11种隶属度函数，比较典型的有梯形隶属函数（trapmf）和三角形隶属函数（trimf）等。本文采用三角形隶属度函数，MATLAB表示为：

其中，参数A表示三角形左“脚”数值，参数C表示三角形右“脚”数值，参数B表示三角形“峰”值。三角形隶属度函数表达式如下：

其中车速模糊集论域为[0，120Km/h]，分为5级。质心侧偏角论域为[0，13deg]，分为12级。转向角论域为[0，17deg]，为实现较高的控制精度，分为16级。补偿制动压力论域为[0，11Mpa]，分为16级。模糊变量隶属度函数，如图4所示。

图4 模糊变量隶属度函数

根据附着椭圆理论，车辆高速爆胎瞬间，轮胎参数发生突变导致最大附着力减小，控制制动轮缸输出较小制动力，转向盘输出较小转向角，防止轮胎纵向力与侧向力突破最大附着力，因此提高车辆稳定性。车速较低，控制制动轮缸输出较大制动力，转向盘输出较大转向角，可充分利用最大附着力来减小车辆偏航程度，因此提高车辆制动安全性。通过隶属度函数，分别建立了质心侧偏角和车速与转向角、质心侧偏角和车速与制动压力的模糊规则。模糊控制规则表，如表1所示。

表1 模糊控制规则表

模糊控制器根据质心侧偏角β和质心车速V确定所需补偿制动压力ΔP，补偿制动压力ΔP再分配到所需爆胎轮缸。分析爆胎后偏航原因可知，爆胎引起的轮胎参数发生突变无法通过Carsim实现，因此，在建立线性二自由度车辆Simulink模型中，侧偏刚度Kf和Kr变化可运用Simulink中工具箱Signal Builder模块完成。将爆胎导致轮胎参数变化模型通过二自由度Simulink模型导入到Carsim软件，实现仿真模型搭建。

由模糊控制器确定补偿制动压力ΔP和前轮转向角δ之后，建立Carsim和Simulink联合仿真模型，如图5所示。联合仿真模型主要由线性二自由度车辆模型、模糊控制模块和ABS防抱死模块组成。ABS模块输入分别为车辆质心速度V、模糊控制器确定补偿制动压力ΔP、制动轮缸压力和各轮缸车速，输出四个轮缸的最终制动压力。Carsim设置车辆第4秒左前轮发生爆胎，模糊控制器确定的补偿制动压力ΔP仅输入到ABS模块左前轮制动轮缸，其它制动轮缸制动压力保持不变。

图5 Carsim和simulink联合仿真模型

4 爆胎控制仿真

车辆参数，如表2所示。车身结构参数、悬架参数、轮胎参数等直接利用Carsim模型默认值，进行了车速、纵向位移、横向位移、横摆角速度、左右前轮制动压力的仿真。

表2 车辆参数

自动驾驶汽车爆胎之前在附着系数0.85路面以120km/h直线行驶，节气门开度为0，设置车辆在第4秒时左前轮发生爆胎，仿真过程中不考虑爆胎轮胎垂向刚度变化，爆胎0.2秒之后，CO增大20多倍，Kf下降为原来的0.28倍[9]，通过模糊控制仿真实验，车速和纵向位移，如图6所示。

图6 车速和纵向位移

由图6(a)可知，自动驾驶汽车在路面附着系数为0.85的路面上，节气门开度为0，滑行4秒车速从120km/h减速到110km/h，经过爆胎控制，车速在8.2秒左右减速到0。由图6(b)可知，自动驾驶汽车在4.2秒时，纵向位移达到146m左右；车速为0时，纵向位移约为175m。在爆胎制动控制过程中，制动距离约为29m。传统汽车初速度110km/h制动成绩约为40m，通过对比，这由于车辆发生爆胎滚动阻力系数瞬时增大，制动距离减少约11m。通过模糊控制仿真实验，横向位移和横摆角速度，如图7所示。

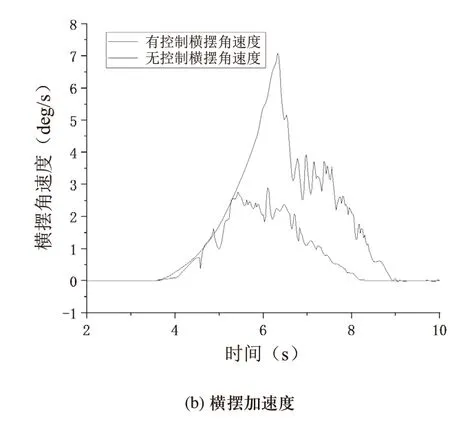
图7 横向位移和横摆角速度

由图7(a)可知，自动驾驶汽车爆胎后，无控制时横向最大位移接近6m，有控制时横向最大位移减小到2m。由图7(b)可知，自动驾驶汽车爆胎后，通过点刹的控制，在模糊控制介入作用下，有控制时横摆角速度在爆胎之后2s左右递增到2.5deg/s，微调前轮转向角方向使横摆角速度减小，自动驾驶汽车偏航程度也随之减小。无控制时横摆角速度达到7.5deg/s，后保持在3deg/s。由于左前轮发生爆胎，左前轮滚动阻力比右前轮大。无控制时，自动驾驶汽车爆胎后驱动力、制动力和侧向力突破了最大附着力，导致车辆发生侧滑甚至轮胎脱辋，因此，横向位移和横摆角速度显著增大。根据附着椭圆理论设计的模糊控制器，使左前轮轮缸爆胎开始采用点刹方式，左前轮轮缸制动压力处于动态平衡中，防止左前轮纵向力和侧向力突破最大附着力，提高车辆稳定性。而右前轮制动强度大，充分利用最大附着力，因此提高车辆制动安全性，实现稳定性控制。通过模糊控制仿真实验，轮缸制动压力，如图8所示。

图8 轮缸制动压力

由图8(a)和图8(b)可知，车辆左前轮爆胎时，在模糊控制器介入的工况下，通过模糊控制规则获得间断的制动压力，右前轮获得相对连续的制动压力，左前轮滚动阻力比右前轮大，但左前轮为间断制动压力，仍能满足最大附着力。因此，左、右前轮制动压力符合附着椭圆理论，满足模糊控制规则，进一步证明Carsim和Simulink联合仿真模型的准确性。

5 结语

针对自动驾驶汽车存在爆胎的问题，基于附着椭圆理论，本文提出了点刹和微调前轮转向角的方式建立模糊控制器，不需要建立具体的数学模型，能够较好地输出自动驾驶汽车爆胎后各轮缸所需补偿制动压力ΔP和前轮转向角δ，从而使爆胎后纵向力和侧向力平方和满足最大附着力。对车速、纵向位移、横向位移、横摆角速度、左右前轮制动压力进行了仿真分析，结果表明：自动驾驶汽车发生爆胎后，无控制横向最大位移接近6m，有控制横向最大位移减小到2m；无控制横摆角速度达到7.5deg/s，后保持在3deg/s，有控制横摆角速度在爆胎之后2s左右递增到2.5deg/s随之减小，提高车辆制动安全性和稳定性。