缺乏边缘信息的圆中心定位

吴光宇，胡之瀚，叶霆崴

（苏州北美国际高级中学，苏州 215104）

0 引言

大型产品，例如导弹、卫星、发动机等作业安装对接质量在一定程度上影响了其安全性和稳定性，国内的对接作业基本采用V型定位支撑的人工装配对接，其安全和质量主要依靠安装人员的经验以及技能水平，安装精度以及稳定性无法保证，传统的方法已经无法满足目前快速发展的自动化生产行业需求[1～3]。

目前，有些学者利用多机器人系统或是力反馈进行对接定位，例如，北京卫星环境工程研究所的代卫兵等[4]，基于并联调姿平台实现力反馈下的柔性对接，北京航空制造研究所的杜兆才等[5]，提出了基于多台三坐标直角机器人协调操作对接系统，这种定位装置承载能力大、适应性强，但控制技术难度大、精度相对较低。上述对接装置都需要人工参与，效率较低，无法满足自动化的生成应用。

圆孔一般被认为是装配过程中的基准，为了达到自动化生产应用，有一部分学者利用机器人视觉伺服引导装配的技术，通过检测安装孔位或辅助销钉进行对接装配，目前常用的方法是使用Hough圆检测方法[6]，该方法计算效率低且精度不高。随后出现了Hough圆的改进算法，但是仍然未能达到较高的精度，而且对边缘的依赖性比较大。还有一部分学者使用聚类的方法进行椭圆提取，该方法将所有的椭圆按中心位置进行聚类[7,8]，将椭圆间中心距在一定范围内的椭圆归为一类，从而实现圆的检测，但是该方法使用了聚类，聚类使得算法效率降低，不能应用于自动化生产中；沈夏炯等[9]，利用连通区域标记算法实现了圆的检测，虽然克服了Hough圆检测缺点，但是当图像采集得到的圆形外轮廓效果不佳时，直接影响下一步的处理结果。中科院沈阳自动化研究所的李展等[10]，利用线结构光对空间目标进行测量，在检测过程中不仅使用圆形带有凹槽的对接环，限制了该方法的使用，而且使用激光跟踪仪等装置，测量效率较低。

实际生产作业中工况较为复杂，圆形零部件可能存在边缘磨损较为严重的情况，磨损的边缘对识别造成了极大的干扰。利用边缘进行识别，势必无法进行检测，导致自动化对接误差较大，因此，本文针对大型部件对接装配过程，提出了一种在缺乏边缘信息情况下的圆中心定位方法，为后续的对接提供基础。

1 复杂工况下大型部件对接装置

对接装置结构如图1所示，该装置主要由一个机器人、机器人控制器以及双目视觉传感器和工控机等单元组成。

图1 装置结构图

具体工作过程为：预先对视觉传感器以及机器人进行标定，CCD相机同步采集被测图像，图像处理单元对采集的缺乏边缘信息的图像圆中心位置进行检测，利用极线约束对圆中心进行匹配，重建圆形区域的中心三维坐标，然后将圆中心在相机坐标系下的三维坐标转换到机器人坐标系下，引导机器人进行对接。

2 基于高斯差分图像和最大稳定极值区域的圆形区域中心定位方法

针对大型产品在对接过程中工况复杂以及实时性要求较高的需求，本文构建了双目视觉引导的机器人对接方法，如图2所示。

图2 对接装置流程图

2.1 预处理

为了得到圆形区域中心的三维信息，需要对双目传感器进行标定，标定相机的内参数矩阵以及相机坐标系之间的转换关系。同时为了实现机械臂辅助对接，需要对相机坐标系和法兰坐标系之间的位置关系进行标定，即手眼标定。

为了方便操作，在手眼标定的同时进行双目视觉标定，借助于最小二乘法，得到双目视觉坐标系转换矩阵以及各自的内参矩阵[11]以及相机坐标系和法兰坐标系之间的转换矩阵[12]。手眼标定的过程如图3所示。

图3 机器人手眼标定

2.2 图像处理

2.2.1 生成高斯差分图像

为了使得图像在尺度变化下具有不变性，需要将采集到的原始图像在所有尺度下做到尺度无关，因此利用高斯金字塔生成高斯差分图像，具体步骤如下：

1）利用高斯卷积核和图像进行卷积建立图像尺度空间，定义图像尺度空间为L（x，y，σ）：

其中，I（x，y）为原始图像，G（x，y，σ）是均方差为σ的高斯核函数，即，⊗表示卷积操作。

2）利用不同尺度对图像进行高斯卷积，形成高斯金字塔的第一组图像，对第一组图像中的倒数第三幅图像进行降采样形成新图像中金字塔第一层，再利用不同的尺度对新图像进行高斯卷积，形成高斯金字塔的第二组图像，不断重复以上操作，建立由多组尺度空间图像构成的高斯金字塔[13]。如图4所示。

图4 高斯金字塔

3）利用相邻尺度的高斯金字塔图像相减得到高斯差分图像，高斯差分图像可以表示为：

在选取金字塔组数时，竟可能选择高的组数，因为组数越高，查找目标所需的时间越短，另一方面，为了保证目标图像的结构清晰，本文中金字塔的组数设置为level=5。

2.2.2 尺度空间极值区域（SSER）检测

最大极值稳定区域（MSERs）指的区域的面积不会随着灰度值得微小变化而产生差异，在一定范围内是相对稳定的，并且MSERs区域还具有仿射不变性。

因此本文结合图像差分高斯金字塔和最大稳定极值区域方法，在图像差分高斯金字塔中提取尺度不变极值区域，将在图像的高斯差分尺度空间相邻尺度上都具有最大极值稳定性的区域被认为是尺度空间极值区域Si，定义为：

其中，i是高斯差分图像Di的级数，i-1，i+1是Di相邻尺度的级数。

因此，尺度空间极值区域具有仿射不变性和尺度不变性[14]。

2.2.3 滤出SSER嵌套区域

由于存在重叠的相似区域，因此需要对相似区域进行精选，最终得到精确的SSER区域，如下图所示，精选原则如式(2)所示：

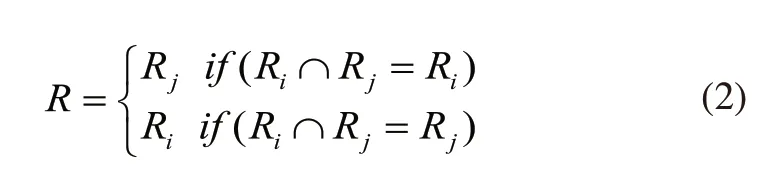
其中，R是滤除嵌套之后的区域，Ri，Rj分别是SSER的第i和第j个区域。

椭圆可以更好的表达一个区域的各种信息，因此为了便于区域的特征描述，需要将检测到的SSER区域进行椭圆拟合，得到尺度不变极值稳定区域的重心，即椭圆中心。

2.2.4 匹配

极线约束可以将匹配点从整副图像寻找压缩到一条直线上寻找，极大缩小了寻找范围。记左图上的圆中心点p1，利用已知的两相机之间的内参数以及坐标系之间的转换矩阵，可以求得p1点在右图上的极线方程，p1所对应的点p2即在该极线上。因此需要引入其他约束来确定p2。若该极线上在右图上只通过一个圆心点，可以直接获得对应点的位置。若该极线在右图上通过多个圆中心。则需要利用其他方法进行选择。本文借助于SIFT描述符[15]进行精细匹配，即可得到唯一的图像匹配点。

3 实验

为了验证提出方法的有效性和正确性，图1为装置结构图，该系统选用ABB机器人，机器人末端安装有双目视觉传感器用于识别实测量，夹具用于部件之间对接。采用basler品牌300w像素相机，配有Computar公司的8mm镜头，相机帧率为10fps，用于对目标进行定位。所有的仿真实验均在Windows 7操作系统下采用Visual Studio 2008软件实现。

3.1 视觉传感器标定

左相机的内参矩阵相机内参矩阵KCL和畸变系数矩阵fCL：

右相机的内参矩阵相机内参矩阵KCR和畸变系数矩阵fCR：

以左相机坐标系为相机基准坐标系，右相机转到左相机的旋转向量R和平移向量T为：

手眼标定的矩阵D为：

对该结果进行重投影，利用标定板两个点之间的距离为固定值作为已知量，如表1所示，表中的数据中列指的是标定板中的7列，利用双目视觉得到标定板上圆心标志点的三维点坐标，并且计算两两点的空间距离，并且计算空间距离误差。从表中可以看出双目视觉精度大于0.02mm。

表1 标定精度

3.2 缺乏边缘信息的圆形区域中心测量

图8 显示待对接产品A 面圆形区域中心检测结果图。

图8 待对接产品A面圆形区域检测

其中，图8(a)和图8(b)分别为左相机和右相机的检测结果图，图8(c)和图8(d)以及图8(e)和图8(f)同理，只是移动了机器人末端的位置使得图像的角度不一样和亮度不一样，从图中可以看出，该方法具有尺度不变性以及旋转不变性，在圆边缘不明显或是缺乏的情况下，仍然能够精确的确定圆区域的中心位置。

表2为图8在圆形区域检测误差，X，Y，Z分别是图8(a)和图8(b)在左相机重建出的四个圆中心三维坐标值，通过计算相邻两个圆中心之间的测量值和三坐标测量的距离进行比对，得到圆中心的检测误差，测量精度为，圆个数为m+1，εm为相邻两圆形区域中心的检测误差，由表2 可以看出，误差精度为0.117637mm。其中，使用的三坐标测量仪的测量精度为（1.6+L/333）um。

表2 待对接产品A面圆形区域检测误差（mm）

图9显示待对接产品B面圆形区域中心检测结果图。

图9 待对接产品B面圆形区域检测

表3 待对接产品B面圆形区域中心检测误差（mm）

其中，图9(a)和图9(b)分别为左相机和右相机的检测结果图，图9(c)和图9(d)以及图9(e)和图9(f)同理，只是移动了机器人末端的位置使得图像的角度不一样和亮度不一样，从图中可以看出，该方法具有尺度不变性以及旋转不变性，在圆边缘不明显或是缺乏的情况下，仍然能够精确的确定圆形区域的中心位置。

4 结语

本文针对缺乏边缘信息无法进行圆中心定位的问题，研究了一种尺度不变极值稳定区域检测方法，该算法在检测稳定区域时不需要考虑区域边界信息，利用在高斯差分图像上进行最大稳定极值区域检测得到具有尺度不变的区域特征信息，当图像在尺度变化大的情况下，也能对圆中心实现三维重建，同时借助最大稳定极值区域的仿射不变性，该区域也具有仿射不变性。通过实验论证，该方法的鲁棒性好，效率高，可以应用于自动化生产中。对于视觉检测存在的误差，为了避免在对接过程中发生碰撞，在视觉引导机器人到达目的后，采用现有比较成熟的研究成果借助于力反馈控制将大型产品部件准确定位，保证对接受力在安全范围内。

在后续的工作中，需进一步分析当圆形区域缺失较大的情况下如何进圆中心定位问题，增强算法的普适性。