盾构施工地层可掘性及对机-岩状态识别案例分析

张沛然，杨果林†，吕涛，陈亚军，邱明明

（1.中南大学 土木工程学院，湖南 长沙 410075；2.中建五局土木工程有限公司，湖南 长沙 410004；3.延安大学 建筑工程学院，陕西 延安 716000）

近年来，随着城市化的快速推进，以地铁为代表的地下工程建设规模迅速扩大，预计到2020 年我国城市地铁建设里程将达到近6 000 km，所需要的施工掘进装备总计500 台以上[1-2].但是，目前盾构施工中存在的问题依然突出，核心原因是对机-岩工作状态关系认识的不足.首先，现有盾构隧道的分类标准仍主要以稳定性为前提，而已有学者[3]明确指出：盾构隧道的围岩分类分级应以可掘性为基础，因为可掘性决定了盾构的施工速度[4]，直接影响工程建设投资成本，根据现有隧道围岩分类方法难以形成适用于盾构施工的指导和操作标准.另外，现有基于地质勘探的隧道围岩调查分类受钻孔取样的随机性[5]和钻探试验误差影响，其全面性以及反映隧道沿线地层地质条件的可靠度均值得商榷，关键的是根据现有技术方法的岩土分类分级结果在盾构施工环节的应用中存在一定的局限性.盾构施工中产生了大量自动记录数据，基于可钻性的研究成果[6-7]有理由相信其中蕴含着值得挖掘、分析和利用的宝贵资源.针对这些问题，已有学者尝试通过分析盾构机的单一施工参数（如推力、刀盘扭矩和推进速度等）变化识别地层条件，但是研究结果受隧道地质或盾构设备的不同其差异性比较明显，难以形成可靠的普遍性共识.因而，转向通过多参数拟合分析[8-9]、神经模型[10-11]和模糊理论[12]等的引入分析研究相关问题.在不同研究中，相关指标的形式和计算方法或许存在区别，其实质是将盾构施工中同步产生的大量自动记录数据组成的维数较高的测量空间变换为维数较低的可用于机-岩状态识别的特征空间[13].研究表明盾构施工参数的一些复合指标与岩土条件确实具有一定的映射关系，复合参数基本可以与地层的岩土物理力学参数指标相关联[14-16]，初步可以对围岩进行模糊判别或分类[9，17].同时，其在复杂地层中的响应变化、对特殊地层的辨识[18]、渣土改良和刀具磨损预测[13，19]等研究中的作用充分说明了相关盾构施工参数复合指标对机-岩状态识别的实时性、灵敏性和适用性，显示出巨大的应用价值.综上所述，以建立基于可掘性的盾构施工地层分类分级和盾构机工作状态判定及其性能预测为目标，深入挖掘盾构施工数据，已经逐渐引起业内关注和重视.但是，鲜有研究对目前所采用的各复合参数的合理性及各参数的统一性进行分析总结，共识的缺失一定程度上制约了国内盾构施工数据的挖掘、分析和应用.

本文基于可钻性原理，通过对现有各复合参数的分析，结合相关文献成果，对盾构施工地层的可掘性问题进行梳理和总结.铺以工程案例，探讨基于可掘性的参数指标对机-岩状态识别的意义.最后，讨论了可掘性的相关问题，以期为可掘性和盾构机-岩状态识别的研究和应用提供参考.

1 盾构施工地层可掘性及表示方法

1.1 盾构施工地层可掘性

可钻性作为反映岩石抵抗钻头钻进的阻力[20]或抵抗钻具钻凿能力的定量指标[21]，已在石油、矿山等行业被用于钻凿钻头选择、生产定额编制及地层判别等[22].在可钻性的研究中分为三种钻进方式考虑：旋转式、冲击式和旋转-冲击式，而盾构的掘进开挖主要靠推进力和刀盘的转动带动刀具切割、破碎岩土体，其行为可以被认为是水平方向上的旋转式钻孔行为.因此，根据可钻性的含义可以初步定义盾构施工地层的可掘性：地层抵抗盾构（刀盘）钻进的阻力或抵抗盾构掘进的能力.可掘性反映了地层岩性、盾构以及环境间的关系[22]，不仅表示岩土体抵抗盾构掘进的能力，而且可以表征所掘进地层的岩土体与盾构的接触作用特征.不同地层的物质组成、颗粒级配、液塑限、强度、硬度和温度等物理力学性状或指标不同，其抵抗机械作用破坏的能力也不尽相同[22-23].盾构在不同岩土性状地层的掘进施工表现理论上呈现出一定的差异性，其具体反映在掘进速率、开挖单位体积或进尺所消耗的能量等方面，岩土性状相同或差异性较小的同类或同级地层的可掘性应该接近或相同.同时，考虑到地层条件的复杂性和盾构机械工作条件的变化，可掘性应该由几个具有代表性的指标组成的低维特征空间表示[13]，用于对掘进地层类别和盾构机工作状态的辨识、评价和反馈.一定意义上组成低维特征空间的几个指标之间根据物理力学机制应形成一定的标准关系，这个标准关系目前可以借助大量的实测数据建立经验模型，因而这项工作具有试验统计性质.

盾构施工地层可掘性研究的重点是提出具有以下两点特征的表示可掘性的合理方法及指标：①从不同角度表示可掘性，如相关专业提出的表示岩石可钻性的三大指标体系-位移指标、强度指标和能量指标[22]，并且理论上这些指标应该具有统一性；②所有指标的计算均应由盾构施工参数直接换算而得，不宜也不应掺加入传统岩土物理力学参数指标.其原因在于，盾构隧道前期工程地质勘察结果难以反映实际沿线地层的岩土条件.同时，保留一定的岩土力学参数数据可以对由盾构施工参数表示的可掘性指标合理性作定性判断.

1.2 盾构施工地层可掘性表示方法及指标

目前，盾构施工地层可掘性研究主要基于盾构施工参数的统计分析，同时考虑到影响可掘性的诸多因素，从严格的物理意义上定义相关指标不具备理论可能性.因此，本文主要探讨从概念性层面表示可掘性的方法，并依托实际盾构工程和国内外相关研究进展归纳性提出各类表示方法的代表性指标.这些指标具备一定的物理机制合理性，是机-岩工作状态的参数反映.

1）位移法及指标：对于具体的盾构隧道工程而言，盾构机掘进所处的地层条件对盾构掘进效率有直接影响，因此盾构的掘进效率一定意义上反映了地层的可掘性.盾构施工现场用于监测、评价掘进效率的指标可以为推进速度或贯入度，其在时间上的累积则为对应时间段内的盾构掘进行程，反之可将推进速度或贯入度视为盾构的瞬时推进行程.为了和可钻性的表示方法一致，本文视盾构推进行程为掘进前进的位移，将以盾构掘进速率表示地层可掘性的方法称为位移方法，简称位移法.盾构的推进速度和贯入度具有如式（1）所示的关系，即在刀盘转速一定情况下推进速度和贯入度成正比.贯入度常被作为现场评价刀盘工作状态的指标，并且在已有的研究中基本上以贯入度作为岩土可钻性或可掘性的试验或现场指标.因此，本文建议在表示盾构施工地层可掘性的位移法中可取贯入度作为其代表性指标.贯入度越大表示盾构掘进时刀盘切入土体的平均切深越大，所受到的地层阻力较小，即可掘性较小.

式中：Prev为贯入度（mm·r-1）；v 为推进速度（mm·min-1）；N 为刀盘转速（r·min-1）.

2）强度法及指标：对于软硬不同的地层而言，如果需要盾构刀盘达到同样的贯入度，则在岩土强度较高的地层中施加的挤压推力理论上应比在强度较低的地层值大，即盾构刀盘推进力的高低与掘进面岩土的强度指标相关联.因此，可以将盾构对于特定掘进面开挖单位深度或切深所需的机械推进力定义为另一类表示可掘性的方法-强度法.定义单位贯入度下的推进力为表示可掘性的一个强度指标，其定义如式（2）所示.事实上单位贯入度下的推进力已在文献中被描述为场切入指数FPI（Field Penetration Index，本文沿用这个名称）、可钻性指数（Drillability Index）和“归一化”推力值等[14]，其物理意义为刀盘贯入1 mm·r-1所需的推进力.理论上岩土的场切入指数越大表示刀盘切入岩土体每单位贯入度的阻力越大，可掘性越大.同时，研究表明场切入指数FPI与地层的岩土承载力、单轴抗压强度（UCS）[15]、岩体完整性系数[24]等均具有一定的相关性.因而，以场切入指数FPI 作为表示盾构施工地层可掘性强度法中的代表性指标，其物理概念明确[17]，也符合可钻性中强度指标以抗压强度、点荷载强度等表示的物理基础[22].

式中：FPI 为场切入指数（kN/（mm·r-1））；F 为总推进力（kN）.

与此同时，如式（3）所示，参照场切入指数FPI的定义，不乏在一些研究中出现了单位贯入度的刀盘扭矩指数TPI.研究表明TPI 值与岩土的物理力学参数具有一定的相关性，但是将其与场切入指数FPI同类考虑的物理意义合理性值得商榷，后文将对此进行讨论.

式中：TPI 为单位贯入度的刀盘扭矩指数（kN·m/（mm·r-1））；T 为刀盘扭矩（kN·m）.

3）能量法及指标：从能量守恒角度而言，盾构机械用于开挖掘进岩土体的消耗功应等同于对应岩土体克服自身强度或稳定性状形成破碎体所需吸收的能量.谭卓英[22]指出岩土的破碎比功只与输入的能量有关，与钻凿工具或掘进机械无关.但是，不同盾构机械因掘进系统能量传递效率的差异使其在相同地层掘进开挖中将会呈现出不同的掘进速率和表现.如上所述，盾构对岩土体的掘进主要靠推进系统顶进和刀盘转动切割、破碎共同做功完成.因而，从能量方面定义盾构施工地层的可掘性可以基于这两部分做功的原理建立而得.根据物理知识可知，推进力在每个瞬时的做功为Fv，而刀盘驱动做功为2πNT，以瞬时推进速度表示的单位掘进体积量为0.25πD2v，则盾构掘进单位岩土体的耗能如式（4），称之为掘进比能（Specific Energy，SE）.

式中：SEf为（现场）掘进比能（kWh·m-3）；D 为盾构刀盘（开挖）直径（m）.

需要指出的是：

1）掘进比能一般分为两种，其一是通过室内岩土切削试验得到的试验SE 值，其二是根据式（4）通过现场实际掘进数据采集计算的现场SEf值.二者在TBM 施工岩层中一般根据岩石的节理、完整性等进行适当折减换算.对于EPB 盾构施工而言，考虑到土仓压力的影响，现场掘进比能SEf值一般高于室内SE 值，文献[25]建议为1.8 倍.

2）现场掘进比能值计算中，认为总推进力和刀盘驱动做功都完全用于掘进面岩土体的开挖中，而实际总推进力包括岩土体抵抗刀盘顶进的阻力、盾壳摩擦力以及盾构前进的机械推进力等.同时，刀盘扭矩也包括刀具在掘进面岩土体中的滚动阻力、正面摩擦、刀盘侧面摩擦、刀盘后部摩擦等[26].根据严格的理论计算各部分具体值，并确定实际切削掘进面岩土体所消耗的有效功，从现有理论研究结果来看，不同工程的理论计算和实测结果均有一定的出入[26-27].重要的是其必须已知掌子面及其附近岩土体的物理力学参数以及岩土体与盾体、刀盘和刀具等的接触力学参数，而这恰是本文基于可掘性所希望解决的岩土参数取值不确定问题，因而在现场掘进比能计算中暂不讨论总推进力和刀盘扭矩的组成及分量问题.

事实上，掘进比能值SEf中推力做功（Fv）所占的比例较小，因而式（4）可以简化为以刀盘驱动做功为主的表达式（5）：

不难看出，对于同一工程而言掘进比能SEf与上述单位贯入度的刀盘扭矩指标TPI 值之间为一种线性函数关系，即TPI 实质可视为表示盾构施工地层可掘性的一个能量法指标.

综上所述，本文从不同物理层面总结提出了表示盾构施工地层可掘性的三类方法：位移法、强度法和能量法，并优选了相应代表性指标.三类表示方法中，能量法相较其它两类的物理意义更为严谨，重要的是能量法可以从能量守恒的角度联系室内外试验和施工数据的分析结果，进而为可掘性从研究到工程应用提供有效途径.但是，位移法或强度法对可掘性的研究和应用而言依然具有重要的价值，比如受限于室内试验设备平台的局限性，二者相较能量法更易获取相关指标.理论上三类方法及其指标应该具有统一性.而这种统一性不仅说明了采用盾构施工参数复合指标表示岩土界面特性-可掘性的科学性，为机-岩工作状态识别研究提供有力支撑，而且为三类方法及指标的相互转化提供研究和工程应用上的依据.

2 某EPB 盾构隧道施工实例分析

2.1 工程概况

长沙市某电力市政管廊盾构隧道工程，总长近6 km，隧道内径3.6 m，开挖直径4.35 m，采用两台土压平衡盾构南北相对施工.据勘测报告，盾构掘进地层地质条件复杂，从南向北盾构掘进经历砾岩、砂卵石、泥岩（泥质粉砂岩）、圆砾、板岩和粉质黏土等地层，其中前三者为主要地层，各地层风化程度不同.

2.2 盾构施工参数及可掘性指标时程变化分析

为对盾构施工参数及本文选取的岩土可掘性代表性指标进行分析，在项目现场依据勘查报告调取保存了包括泥岩、砂卵石和砾岩地层的近150 环盾构掘进数据.其中，各地层风化程度涉及全风化、强风化、中风化以及复合地层等.通过对采集数据的分析，发现每环掘进的施工参数时程变化存在共同的特征，限于篇幅，本文以盾构机在砂卵石地层中某环的主要掘进数据分析为例.如图1 所示，本掘进曲线具有盾构施工参数数据分布变化的代表性特征，结合表1 可以分为以下几个阶段.

表1 盾构不同工作阶段施工参数及可掘性代表性指标统计表Tab.1 Statistical table of construction parameters and representative boreability index of shield in different working stages

图1 盾构掘进过程施工参数和可掘性代表性指标时程变化曲线Fig.1 Time history curve of construction parameters and representative index of boreability during shield tunneling

Ⅰ）启动阶段：总推进力和刀盘转速快速增加，约在60 s 时达到极值A 点，推进速度和贯入度随之分别增加至约60 mm·min-1和40 mm·r-1，在这个过程中场切入指数FPI 和掘进比能SEf降低了一个数量级.但很快推进速度和贯入度随之又发生了急剧降低，在第147 s 时降至B 点，跌至2.0 mm·min-1和1.86 mm·r-1附近，在此期间刀盘扭矩较低，而总推进力并没有发生明显的降低，导致FPI 和SEf在推进速度和贯入度触底时出现了明显的反向震荡，增大一个数量级多.掘进约200 s 时，刀盘扭矩快速增加至1 000 kN·m 附近，推进速度和贯入度则急剧攀升至70 mm·min-1和50 mm·r-1左右，高于A 点附近的对应值，FPI 和SEf快速回落至200 kN/（mm·r-1）和3 kWh·m-3以内.通过以上变化特征可以看出，当刀盘扭矩较低时，由式（2）和式（4）定义计算的FPI 值和SEf值可以快速识别出机-岩状态，即刀盘接触顶进地层的启动阶段.

Ⅱ）顶进掘进阶段：盾构约从150 s 开始，刀盘扭矩快速上升，在222 s 左右时达到972 kN·m，推进速度和贯入度攀升至81 mm·min-1和62 mm·r-1，认为刀盘从对地层的接触进入切入状态.222 s 以后盾构进入正常掘进阶段，此阶段总推进力相对较为稳定（7 289～8 027 kN），刀盘扭矩约在426～1 003 kN·m间变化，具有一定的震荡性，此阶段的贯入度均值约为55 mm·r-1，为盾构不同工作阶段的最大值.推进速度和贯入度的震荡趋势基本同步于刀盘扭矩的变化，说明盾构在正常掘进阶段的刀盘工作状态是影响贯入度和推进速度的主要因素[28].正常掘进阶段，FPI 和SEf分别在108～716 kN/（mm·r-1）和1.07～6.43 kWh·m-3间变化，变化幅度相对较小，曲线平稳，说明当前地层的岩土条件较为均质.注意到，在正常阶段贯入度和推进速度发生了一次明显跌落（图中D 点），FPI 和SEf值发生了偏离.但此刻刀盘扭矩并未发生显著性变化，说明D 点是施工中的一个异常状态，在正常分析中应该予以剔除.

Ⅲ）停机阶段：在盾构掘进至约936 s 时，总推进力、刀盘扭矩和螺机扭矩等均发生了显著回落降低，此阶段的贯入度均值落至0.87 mm·r-1左右，为盾构不同工作阶段的最小值，FPI、TPI 和SEf值均发生了剧烈震荡.结合现场施工情况，此时盾构渣土车进行换车，盾构处于（临时）停机状态.在盾构临时停机结束后，各项参数回归正常掘进阶段状态，直至掘进完成.

从以上盾构掘进阶段的全过程分析可以看出，刀盘扭矩和总推进力发生显著性变化时对贯入度、推进速度产生了明显影响，同步影响可掘性代表性指标的变化趋势，相关变化特征与文献[14，24]研究结果基本一致.

3 可掘性表示指标的统一性

3.1 盾构不同工作阶段和典型地层的统一性分析

如图2 所示，本文分别对2.2 节所述盾构不同工作阶段，以及三大地层近150 环未经筛选包含各掘进阶段的可掘性指标进行了统计分析.可以看出，无论单环盾构掘进的不同阶段或是三类地层的可掘性代表性指标间关系而言均具有显著的相关性.场切入指数和掘进比能随贯入度增大而降低；掘进比能随场切入指数的增大而同步增加，表明抵抗刀盘切入的阻力越小，其刀盘贯入度越大，同时掘进时所需要消耗的能量越少.各可掘性代表性指标变化曲线上呈现出鲜明的聚类特征，掘进阶段较大的贯入度对应的场切入指数相对较低且稳定，而当贯入度不断降低，其对应的场切入指数以数量级式连续增加，特别是在停机阶段贯入度频近于0 时，场切入指数达到万位数.而启动阶段和顶进阶段贯入度主要分布于5～40 mm·r-1，低于掘进阶段的均值55 mm·r-1.同时，启动阶段的数据不同程度地偏离各指标关系拟合线，说明启动伊始盾构机的施工参数受机-岩接触状态的影响呈现较大的离散型.因此，对于一个均质连续的地层而言，由三类可掘性表示方法及其指标表征的地层可掘性及其范围应该是确定的.当各指标远离这个正常范围，往往是机-岩状态异常的征兆或表现[13，18].

图2 某环不同掘进阶段和典型地层盾构施工地层可掘性代表性指标相关性分析曲线Fig.2 Correlation analysis curve of representative indexes of boreability in different driving stages of a ring and typical strata

从图3（a）可以看出，每个地层的掘进速度具有一定的聚类特点，推进速度与贯入度成正比，而采用贯入度表示位移指标可以消除不同地层中刀盘转速对推进位移计算的影响，说明选取贯入度作为位移法的代表性指标是合适的.如图3（b），采用式（6）计算的掘进比能SEf-T 与基于式（4）求得的掘进比能SEf-（T+F）结果相近，经计算SEf-T 值约为SEf-（T+F）的96%，说明盾构掘进中破碎开挖土体的主要能量来源于刀盘系统.如图3（c）所示，掘进比能SEf与式（3）定义的TPI 值成线性关系.

图3 三类地层的施工参数及可掘性指标相关性分析曲线Fig.3 Correlation analysis curve of construction parameters and boreability indexes of three typical strata

3.2 不同盾构工程可掘性表示指标统一性分析

如表2 所示，从国内外学者[9，13，28-34]的研究结果可以看出，本文所归纳提出的可掘性代表性指标间相关性较好.其中，位移法和强度法指标分别与能量法指标间为典型的幂函数.但是，有关研究主要针对TBM 施工，较少涉及EPB 盾构施工方面.为此本文根据文献[29]对近150 环施工数据进行了掘进阶段的可掘性指标计算（说明：本盾构共16 把滚刀），结果如图4 所示.可以看出，各地层的可掘性指标具有鲜明的聚类特征，泥岩地层的场切入指数和掘进比能相较砾岩和砂卵石地层而言分布较为广泛，或与地层的液塑限[30]和风化程度有关.但是，受砂卵石地层土水压力和卵石强度等影响，相同贯入度下砂卵石地层的FPI 值高于其他两类地层.

图4 不同工程的可掘性代表性指标相关性对比分析曲线Fig.4 Correlation analysis curve of representative boreability indexes of strata of different projects

表2 盾构施工地层可掘性指标间相关性统计表Tab.2 Statistical table of correlation among boreability indexes of shield construction strata

综合而言，本EPB 盾构工程施工地层的可掘性指标相关性同各文献研究结果基本一致，说明三类可掘性指标可用于TBM 或EPB 盾构施工地层的可掘性表示.值得注意的是，当贯入度小于20 mm·r-1时，本文计算的场切入指数较大于文献中的研究结果，说明采用EPB 盾构施工时刀盘每转切入深度所对应的推进力更大，刀盘需要更大的顶进破碎压力.但是，随着贯入度的增大，采用文献公式的推算值将趋近落于本文的95%预测区间内，此时可以用统一的函数表达场切入指数和贯入度的关系，如式（7）.

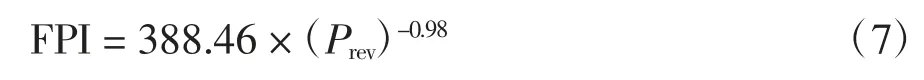
如图4（b）所示，对于掘进比能SEf和贯入度Prev之间的关系而言，本文统计结果与文献值基本相趋近.说明对于不同工程而言，虽然采用的TBM 或EPB 盾构设备可能不同，所面对的地层条件也可能千变万化，但是从能量守恒角度而言，掘进开挖一定岩土体所消耗的能量多少不因设备、作业方式等发生改变[22]，这为我们制定盾构施工地层可掘性分类分级标准或体系提供了科学依据.另外，如图2（c）、2（f）和4（c）所示，掘进比能和场切入指数的拟合结果也取得了较好的相关性.同时，结合图3（b）对于盾构掘进土体能量来源贡献的分析结果，可以为掘进比能与场切入指数之间的高度相关性提供有力解释.虽然采用式（3）定义计算的掘进比能中包括了推力做功一项（Fv），但是其对掘进比能贡献非常低，数学意义上掘进比能与场切入指数之间不存在耦合影响，二者的高度相关性为本文选择的三类可掘性表示方法及其指标合理性提供了有力解释.

4 机-岩状态识别案例分析

如图5（a）所示，本盾构在掘进至里程DK1+880附近时，盾构在进入正常掘进阶段后，其贯入度却难以提升.期间，贯入度均值为5.45 mm·r-1，且小于1.0 mm·r-1的贯入度占统计数的50%以上，远低于图2和图4 中砂卵石贯入度20～60 mm·r-1的掘进水平.但是，掘进阶段的刀盘扭矩和总推进力却远高于砂卵石地层的正常水平，特别是总推进力大于8 000 kN 的占统计数80%以上，高于1 000 kN·m 的扭矩值占比超过40%.如图5（b）所示，掘进阶段的掘进比能和场切入指数均值异常高于前文砂卵石地层的正常范围.经统计，掘进比能大于10 kWh·m-3的占70%以上，场切入指数小于500 kN/（mm·r-1）的不足10%，而图4 中47 环砂卵石地层的最大场切入指数值均远低于500 kN/（m·r-1），掘进比能也均低于10 kWh·m-3.从图5（c）可以看出，特殊地层的场切入指数和掘进比能均较后续砂卵石地层出现一个数量级以上的变化.因此，无论从施工参数的单独变化或是对可掘性代表性指标的分析表明本区段内盾构施工表现异常.结合现场出渣情况来看，其地层条件已不符合地质勘查中连续砂卵石地层的结论，盾构掘进实质进入了特殊地层.

图5 特殊地层中施工参数及可掘性指标变化曲线Fig.5 Change curve of construction parameters and boreability indexes in special stratum

事实上，在进入DK1+880 以前盾构机施工参数的异常已经出现，但未引起工作人员的重视，使盾构机进入了难以前进的状态.当晚第1 次掘进24 min实质推进16 mm；第2 次试掘进7 min 失败，停机36 h；第3 次掘进11 min 前进14 mm 后被迫停工.与本文的可掘性表示方法相似，文献[18]结合掘进参数提出了修正比能，利用BP 神经网络技术对盾构掘进过程中的孤石地层进行了准确识别.综上所述，根据传统地勘采取抽样钻孔勘探对盾构隧道沿线掘进地层进行调查评价，所得结果的全面性和真实性值得商榷.而可掘性指标在特殊地层中具有较好的响应机制，可以对机-岩状态做出及时反馈，未来通过基于可掘性表示方法和指标的超前地质预报技术将为盾构施工提供有效指导.

5 问题及思考

上述研究表明,基于盾构施工参数建立的表示可掘性的方法和指标可用于对地层以及机-岩状态的识别、评价，具有较好的合理性及应用性.问题的关键是在明确和选择了可掘性的三类表示方法及指标后如何解决以下几点关键性问题[21]：

1）进一步对可掘性的含义及表示方法进行深入研究，建立基于可掘性的盾构施工地层分类分级方法、标准和体系.

2）开展传统地勘及岩土测试试验结果和盾构施工参数的统计分析工作，逐步由地勘调查方法向基于可钻性、可掘性的随钻勘测技术过渡，形成盾构施工地层地勘工作新的方法、技术及标准.

3）利用大数据技术、模糊聚类和神经模型等理论方法技术等对盾构施工的时变参数进行认知、处理、分类分级和可视化.

4）提出盾构施工地层识别、预警和机-岩状态反馈调节的方法与技术.

表3 为国内外针对可掘性与岩土物理力学参数相关性研究的部分结果.可以看出，以单轴压缩强度[9，15，24，34，36，39]为主要参数，辅以完整性系数[9，24，34]、节理[37]和液塑限[30]等指标形成了相关研究的特色.其中，相关系数从0.22 到0.968 3 均有所分布，因而，要形成评价可掘性的完善物理力学指标计算方法还需要进一步的深入研究.同时，受地勘调查的样本随机性和数量影响，很难对盾构隧道的施工提供全面的科学依据和有效指导.因此，对于问题（2）的认识和解决可以将目光转换至近年来出现的随钻技术及其相关研究[6，7，22].

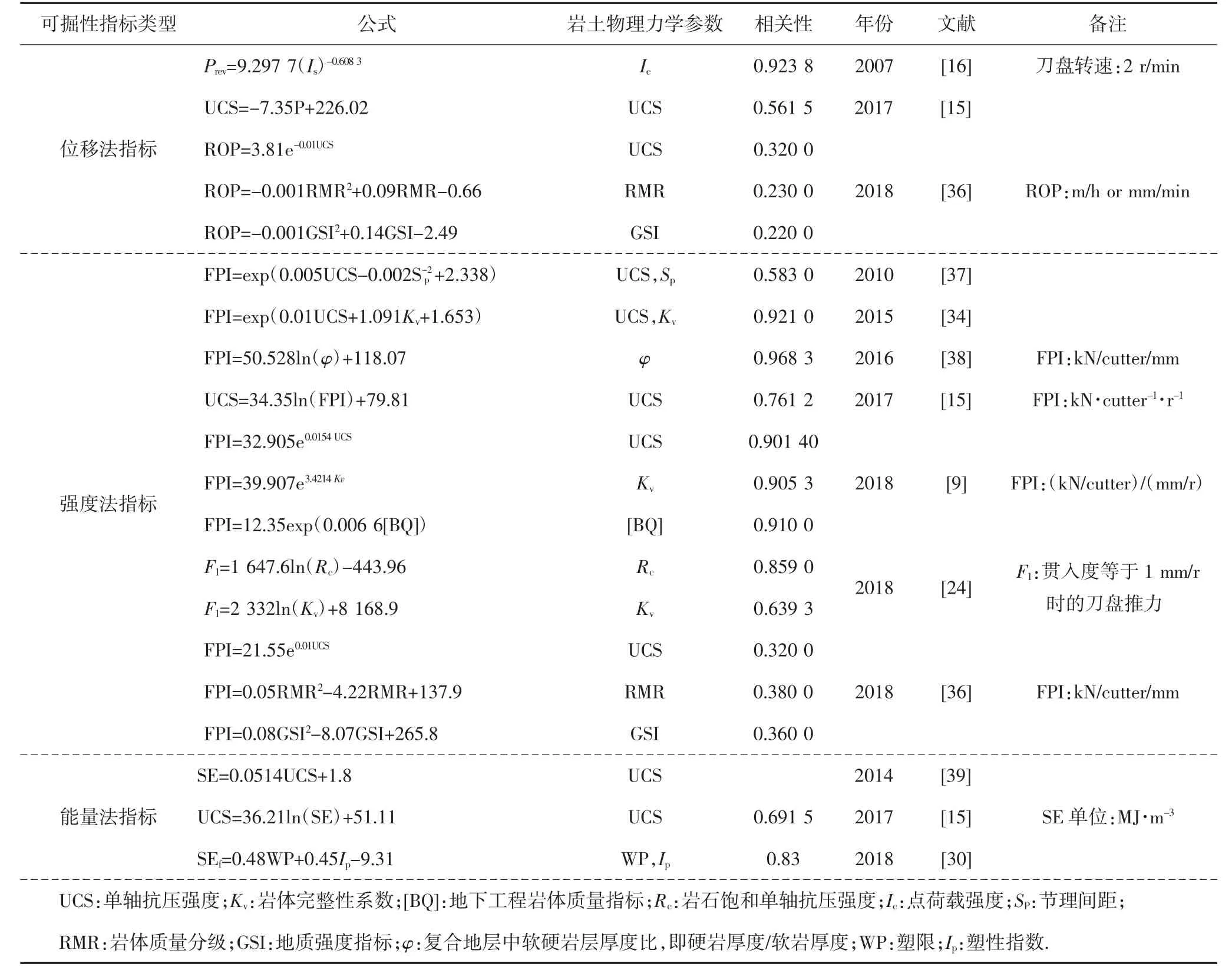
表3 盾构施工地层可掘性指标与岩土物理力学参数关系统计表Tab.3 Statistical table of relationship between boreability index and physical and mechanical parameters of rock and soil

6 结论与建议

1）通过对盾构掘进过程的物理机制分析，认为可掘性表示地层抵抗刀盘钻进的阻力或盾构掘进的能力.总结提出了表示可掘性的三类方法：位移法、强度法和能量法，并优选了代表性指标.

2）基于实际工程数据的分布特征提出了盾构掘进工作的4 个阶段.发现正常掘进阶段盾构刀盘的工作状态是影响贯入度和推进速度的主要因素，即刀盘驱动是盾构掘进破碎岩土体的主要做功系统.

3）不同方面的研究均表明表示可掘性的三类方法及指标间具有显著的相关性，且在同类地层中表现出一定的聚类特征.

4）在特殊地层中可掘性指标依然具有一定的相关性，说明可掘性指标对机-岩的非正常工作状态具有灵敏的响应特征.

5）盾构施工地层的可掘性研究应在统计分析岩土体主要物理力学参数和可掘性指标关系的同时，加快推进传统地勘向以可掘性为导向的钻探方法技术转变发展.