SmCo5/Co纳米复合多层膜的成核场

王贤彬

（中国人民武装警察部队警官学院基础部，四川 成都 610213）

0 引言

该文采用微磁学方法得到了体系的成核场的解析公式；并通过计算机模拟，得到了SmCo5/ Co 纳米复合多层膜体系的成核场与软、硬磁相厚度变化关系的图线。同时进一步分析成核场与软、硬磁相厚度变化关系的图线，得到了以下结论：1）当体系中的硬磁相变厚时，成核场会变小。2）当体系中的软磁相厚度变厚时，成核场会变大。但是没有呈现出一些文献中所描述的平台和峰值[1]。

1 计算模型

SmCo5/Co 复合多层膜体系由高矫顽力的硬磁相和高剩磁的软磁相复合而成，软、硬磁相交替排列的结构使体系兼顾了软磁相和硬磁相的优点，从而引起了磁学界的高度关注，研究人员对此做了大量细致而卓有成效的研究[1-8]。1993年，Skomski 和Coey 等人[2]利用微磁矢量方程，计算得出纳米复合磁性材料的磁能积可达1 MJ/m3（120 MGOe）的结论，其磁能积大约为NdFeB 磁体理论值的2 倍，这使磁学工作者在纳米复合磁性材料领域看到了希望。Skomski 和Coey 还预言这样大的磁能积将会出现在薄膜厚度非常小的时候，他们认为体系的矫顽力机制表现模式为成核模式[2]。

在现有的文献中，有许多关于纳米复合多层膜体系成核场的成果，但是也存在一些差异。例如Leineweber 等人[3]就对第三代纳米复合永磁材料进行了大量研究，不仅得出体系软磁相厚度对成核场的影响及变化规律，还得出了在软磁相很小时，成核场会出现平台的结论，而且其平台会在软磁相厚度小于布洛赫壁宽度时出现，研究还发现硬磁相磁晶各向异性场与其成核场大小一致。G.P.Zhao 等人[1，3-5]的研究成果却得到成核场随硬磁相厚度变化而单调变化的结论。文献[1]和文献[5]都将硬磁相的厚度假设为无限大，这样虽然简化了计算过程，但是却不能得到成核场随硬磁相厚度变化的关系图像。杨世清等人[7]通过研究发现成核场随软磁相、硬磁相厚度变化而单调变化的关系，但也没有出现一些文献中提到的平台。

2 计算方法

该文对SmCo5/ Co 复合多层膜体系的模拟计算是基于如图1 所示的软硬磁相周期性交错复合而成的结构，这就使纳米薄膜的排列具有对称性，为简化计算，笔者选取纳米薄膜中相邻的两层（如图1（b）所示），其中薄膜的下层为软磁材料Co，上层为硬磁材料SmCo5，同时以两层薄膜相交的中点作为坐标原点，取软磁相和硬磁相厚度的一半，xy坐标轴在薄膜平面内，与各层膜面平行，z轴与xy坐标轴垂直，建立o-xyz三维坐标系。在模拟计算过程中，为简小计算难度，笔者假设膜面为无限大，同时忽略边缘效应，就把模型简化为一维模型。

图1 磁性多层膜模型

在建立模型和计算的过程中，采用单轴各向异性软硬磁材料，其易磁化轴方向是沿x轴的,同时所加的外磁场的方向H是平行于x轴的，也就是平行于取向的计算模型。

根据Brown 的微磁学原理[2-3]，纳米复合磁性材料的能量公式如公式（1）所示[1，5]（CGS 单位制）。

式中：s、h为软、硬磁相；F为总能量；H为外加磁场的大小；θ为磁化强度与外加磁场之间的夹角；A为交换常数；K为磁晶各向异性常数；M为自发饱和磁化强度。

根据所用模型，可得体系的边界条件，如公式（2）所示。

由复合多层膜体系的能量公式和上述边界条件，并结合欧拉方程。

可得出系统能量最小时的磁矩分布，如公式（3）和公式（4）所示。

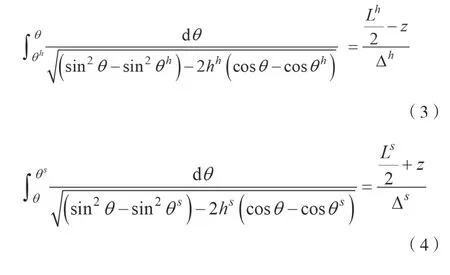
在成核点，磁矩角度偏转很小（θ<<1°），因此对公式（3）和公式（4）进行泰勒展开并积分可得，积分取值为z=0，[θh，θ0] [θ0，θs]，其中θ0为成核点的磁矩偏转角度，θh为硬磁相磁矩偏转角度，θs为软磁相磁矩偏转角度。在积分结果中，用hs=H/Hs k表示软磁相的约化外场，用=2Ks/表示与软磁相对应的磁晶各向异性场，用hh=H/表示硬磁相的约化外场，用=2Kh/表示硬磁相磁晶的各向异性场，软硬磁相的约化外场如公式（5）和公式（6）所示。

带入边界条件，变形结果如公式（7）所示。

求解以上3 个方程，消去θ0，θ s和θ h，可以得到解析后平行取向的成核场公式，如公式（8）所示。

2.4 计算结果及讨论

该文的计算采用了部分物质参数，其数值见表1。表1中共列举了4 种磁性材料的参数数值，该文所得到的成核场随软硬磁相厚度变化的关系图线都是根据相关参数得到的。

表1 物质参数表

2.4.1 成核场随硬磁相厚度的变化

在图2 中，坐标系中的横纵坐标分别表示硬磁相厚度Lh和成核场HN，图2 中的各条图线是在软磁相厚度一定时，成核场随对应的硬磁相厚度改变而改变的情况。对每一条硬磁相厚度相同的曲线进行分析，发现成核场随硬磁相厚度变化而变化的规律几乎相同，也就是当硬磁相厚度均匀变大时，在硬磁相厚度较小时，成核场增大的速度极快；当硬磁相厚度增大到一定程度后，成核场只有微弱的增涨。观察软磁相厚度不同的5 条图线可得，当硬磁相厚度增大时，与之对应的成核场随硬磁相厚度的变化出现非均匀的变化，其随软磁相厚度的增大而快速减小[6]。仔细分析还发现，硬磁相厚度在很小时（Lh≤1 nm)，成核场随硬磁相厚度的变化出现极其明显的变化，这就表明软硬磁相的交换耦合作用相当强烈，可以看出在硬磁相厚度小于交换长度时，两相彼此的交换耦合作用是很强烈的；当硬磁相厚度增大时，硬磁相对成核场的影响减小，出现交换耦合作用削弱的情况，当硬磁相厚度大于布洛赫壁宽度（3 nm）时，体系的交换耦合作用变得非常小，近似消失。

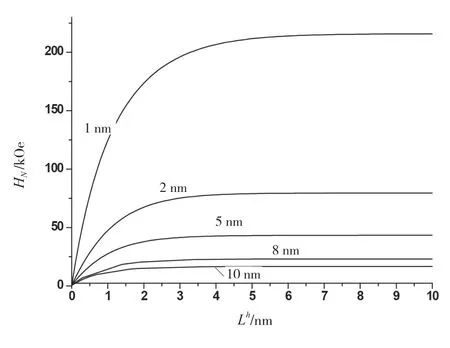
图2 复合多层膜的成核场随硬磁相变化图像

2.4.2 成核场随软磁相厚度的变化

在图3 中，横坐标表示软磁相厚度，纵坐标表示成核场。图像中每一条曲线表示在某一确定的硬磁相厚度下，成核场随软磁相厚度变化而变化的情况。分析发现，硬磁相的厚度不同时，成核场随软磁相厚度变化而变化的趋势是相同的，即当软磁相厚度增大时，其成核场是递减的。而且在软磁相厚度较小时（Ls≤1 nm），成核场随软磁相厚度的增大而迅速减小，当软磁相厚度的变化范围为2 nm～10 nm 时，成核场的减小速度趋于缓和；当软磁相厚度＞11 nm 时，成核场的变化可以忽略，趋于某个定值。通过进一步分析发现，当硬磁相厚度分别3 nm 和5 nm 时，成核场随硬磁相厚度变化而变化的趋势是相同的，即随着硬磁相厚度的增大，硬磁相厚度对成核场的影响变小。

图3 磁性多层膜的成核场随软磁相变化图像

2.4.3 软、磁相厚度的关系图像

通过对图4 的观察分析，笔者发现当成核场为某个定值时，软磁相厚度随磁相厚度变化而变化的曲线在不同的成核场下有相同的变化趋势。当软磁相厚度＜0.5 nm 时，硬磁相厚度随软磁相厚度的增大急速增大，当软磁相厚度>0.5nm时，其增加趋与缓和，在确定的某一成核场下，软磁相厚度增加，但硬磁相厚度趋于定值。当成核场＜8 kOe 时，硬磁相厚度随软磁相厚度变化而变化的趋势更加明显，硬磁相厚度增大的范围更大；而当成核场＞8 kOe 时，硬磁相厚度的变化范围减小，局限在25 nm 以内，此时硬磁相对成核场的影响已经变得非常小了，因此可以忽略硬磁相对成核场的影响。

图4 磁性多层膜的成核场一定时硬磁相厚度随软磁相厚度变化图像

2.4.4 成核场随软硬磁相厚度变化的3D 图像

图5 展示的是成核场随软硬磁相厚度变化而变化的三维图像。左侧图中的三维坐标x、y和z分别表示软硬磁相厚度Ls、Lh和成核场HN。右图是将左图水平顺时针旋转90°而得到的。通过观察可以发现，随着软磁相厚度的增大，成核场最开始呈现出快速、线性减小的趋势。而随着硬磁相厚度的增大，成核场呈现出快速、线性增加的趋势。而且当硬磁相厚度较小时，硬磁相对成核场有非常明显的影响和作用，当硬磁相厚度小于交换长度的1/2 时，硬磁相对成核场的影响更大。当外加磁场增大时，更易驱使畴壁由软磁相向硬磁相移动。当薄膜的总厚度增大时，软、硬磁相对成核场的影响都会减弱；在纳米复合多层膜体系的整个磁化反转过程中，软磁相发挥了极其重要的作用，特别是在软磁相厚度较小时，软磁相厚度对成核场的影响特别明显。

图5 成核场随软硬磁相厚度变化的3D 图像

2.4.5 在成核场减小时软、硬磁相对成核场的影响

图6 磁性多层膜的成核场等比例减小时软硬磁相变化图像

从上述讨论中可以发现，成核场随软磁相厚度减小而单调连续增大、成核场随硬磁相厚度增加而单调增大的结论。基于此，笔者对软硬磁相对成核场的影响进行更深层次的讨论。首先，假设硬磁相厚度为无限大，从而得到硬磁相为无限大时的成核场，再按照一定的比例减小成核场，并得到1 个确定的成核场值，最好得到该成核场值与对应的软硬磁相厚度的关系图线。在成核场减小5% 和 10%时，得到了成核场减小为原来的95% 和90%时与软硬磁相厚度的关系图线，从图线上可以看到，以软磁相厚度为10 nm 为中心，硬磁相对成核场的影响最大的软磁相厚度范围为5 nm

3 结论

成核场HN随软磁相厚度的增大而减小，随硬磁相厚度的增大而增大。这一结果与G.P.Zhao 的结论是一致的[5]。成核场随软磁相厚度的增大呈现单调减小的趋势，即软磁相使成核场减小。当硬磁相厚度Lh＞5 nm 时，软磁相对成核场的变化起主导作用，而硬磁相对成核场的影响几乎可以忽略。随着软磁相和硬磁相厚度的增加，其间的交换耦合作用逐渐增强，整个复合磁体逐渐变成一块刚性磁体，这时成核的一致转动就不会再出现。当软磁相厚度和硬磁相厚度都同时变大时，软硬磁相厚度对成核场的影响会减小，而且此时成核场受到的影响基本是由软磁相造成的[5]。通过对纳米复合磁性材料成核场的研究，为进一步研究复合磁性材料的磁滞回线和磁能积打下了坚实的基础，从而使获得更高性能的新型磁性材料成为可能。