基于数值理论与拓扑优化下电阻式应变传感器灵敏度的研究

胡 斌，廖玉松，谭邦俊

(滁州职业技术学院 汽车工程系，安徽 滁州 239000)

0 引言

目前电阻式应变传感器在军事设备、机器人、医疗器械等领域应用十分广泛[1]。电阻应变式传感器是利用电阻应变片将应变转换为电阻变化的传感器。传感器由在弹性元件上粘贴电阻应变敏感元件构成。当被测物理量作用在弹性元件上时，弹性元件的变形引起应变敏感元件的阻值变化，通过转换电路将其转变成电量输出，电量变化的大小反映了被测物理量的大小。其灵敏度是衡量电阻式应变传感器测量精度的重要指标之一[2]。本文以目前一款电阻式应变传感器为例，首先利用WorkBench有限元软件进行力学分析确定贴片区域。继而结合电阻传感器工作原理与复合梯形公式对有限元得到数组进行处理，分析灵敏度的理论值。最后利用拓扑优化软件对其进行优化设计，从而提高其电阻式应变传感器的灵敏度。图1所示为本文所处理的电阻式应变传感器。

图1 电阻式应变传感器

1 有限元分析

1.1 模型的建立

根据图1所示电阻式应变传感器建立三维模型和有限元网格模型，如图2所示。图2(a)所示的应变式传感器的弹性体敏感元件三维模型建模利用的是三维UG软件。接下来，将建成的三维模型导入WorkBench有限元软件中进行网格划分，划分网格时采用六面体网格，确保有限元求解结果的精度[3]，结果如图2(b)所示。

1.2 工况的设置

工况的设置主要是明确传感器弹性体在实际工作过程中受力情况。该型号传感器实际工作受力情况为一端固定一端施加载荷F，即弯曲梁形式的结构。该型号传感器最大量程为350 kg。在A端施加载荷F=3500 N，B端加载约束地面X、Y、Z三个线位移和三个角位移的自由度[4]，得到以下的有限元加载模型如图3所示。

图3 模型的工况的设置

1.3 结果分析

目前，应变式电阻传感器采用的材料为2A12-T4铝合金，其弹性模量E= 76.8 GPa，屈服强度为395.1 MPa[5]。在WorkBench下完成模型的网格建立，材料的属性、工况设置之后，进行求解，所得结果如图4所示。

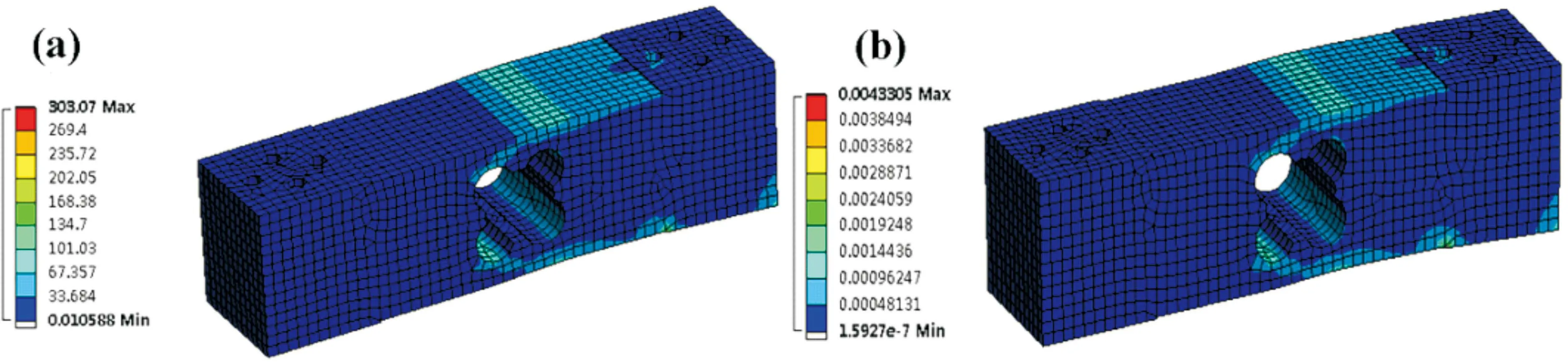
(a)应力云图 (b)位移云图

根据有限元分析得到图4所示的结果云图可知，在满载350 kg下最大应力为303.07 MPa，最大位移为0.00433 mm，出现在传感器的弹性体敏感元件的中部。

2 灵敏度理论计算

2.1 应变片工作原理

应变片由敏感栅1、基底2、盖片3、引线4等组成，如图5所示。当应变片贴在传感器时，通过金属的电阻应变效应，改变应变片电阻的大小。

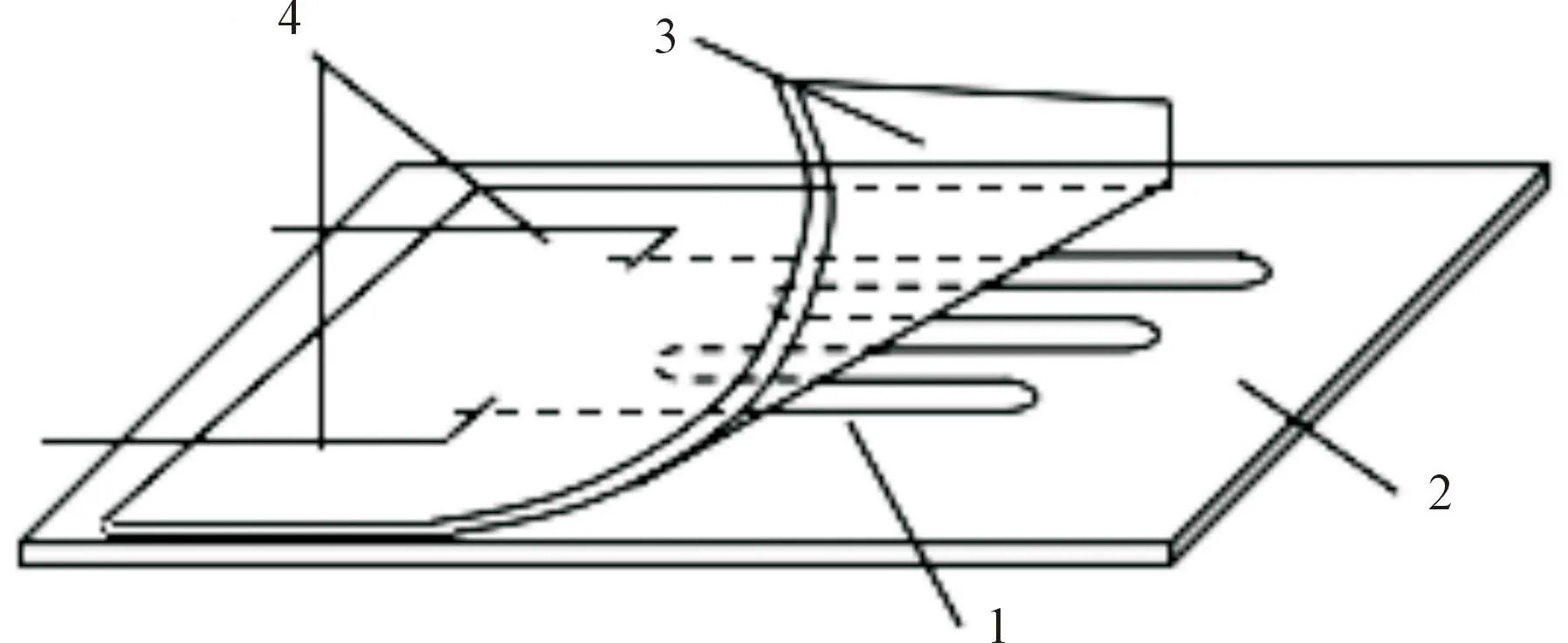
图5 应变片示意

电阻应变式传感器中应变片大小的选择和贴片区域的选择决定了传感器灵敏度的精度，且二者选择并不是孤立的。应变片的规格要考虑贴片区域的大小。而贴片区域的选择要考虑传感器在受力过程中应变最大区域且在贴片区域中应变片的变化趋于平稳，不能出现高低起伏现象。根据有限元计算的结果选择应变片的型号为ZF350-1AA-W(23)N※，其参数为敏感栅尺寸为1.1 mm × 1.0 mm，基底尺寸为2.9 mm × 2.0 mm。

根据有限元计算所得应变最大区域，结合应变片大小选择应变片在传感器上贴片位置，如图6所示。图6中指定的贴片区域应变量最大且应变变化平稳，在该区域贴上应变片后，通过全桥电路容易测量该区域应变的变化。

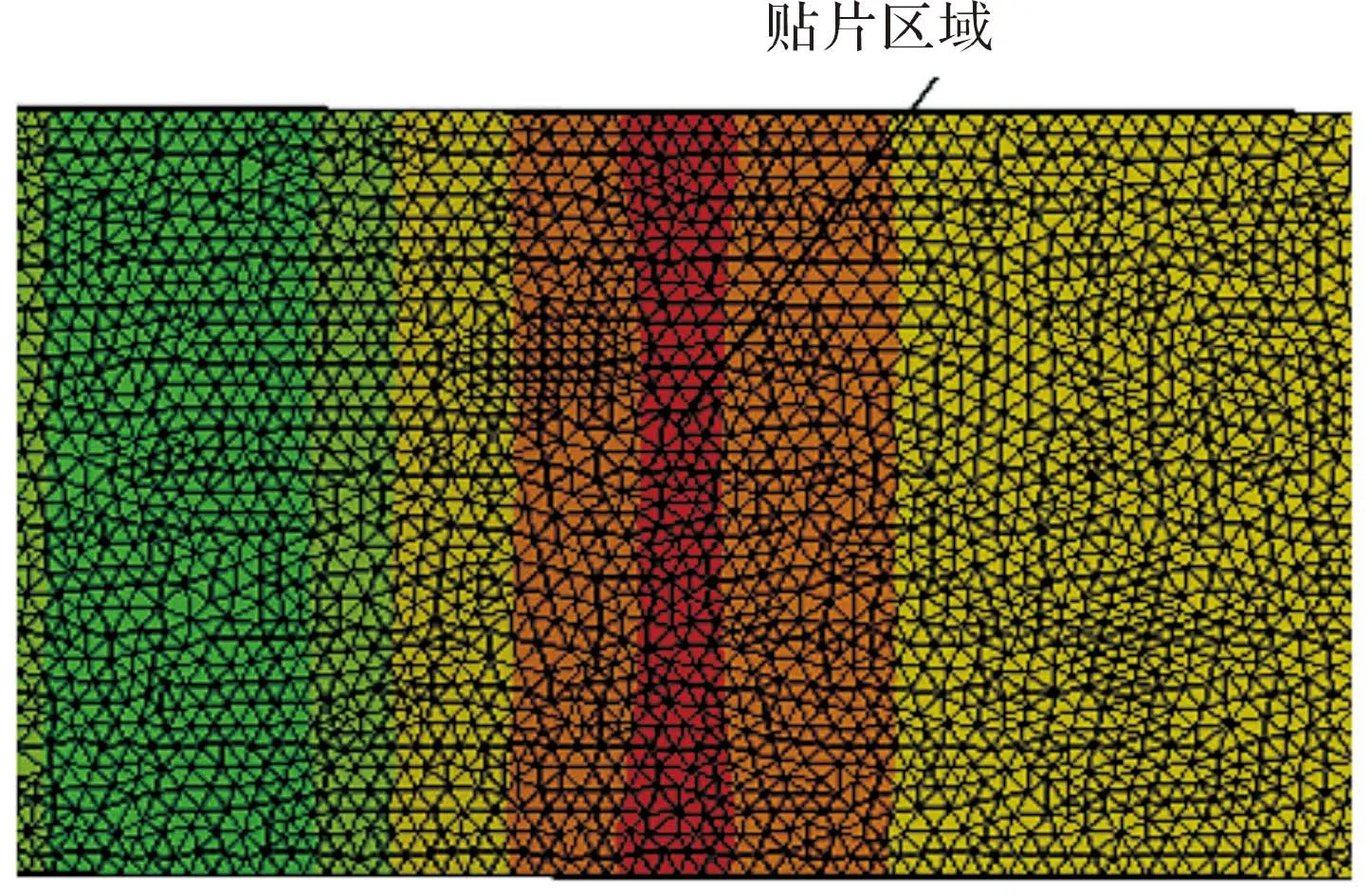
图6 贴片区域

2.2 转换电路的选择

电阻应变式传感器输出的机械应变很小，用一般测量电阻的仪表难以直接测出，必须采用专门电路来测量这种微弱的变化。考虑到全桥差动电路没有非线性误差，且电压灵敏度是单桥电路的4倍，具有温度补偿的功能。在全桥差动电路中直流全桥四臂电路较为常用[6-8]，其电路图如图7所示。图7中R1、R2、R3和R4构成全桥差动电路的四臂，即在R1、R2、R3和R4上贴应变片，其中R1和R4上的两个应变片为拉应变，R2和R3上两个的为压应变。

图7 全桥差动电路

在图7所示的电路中，电桥R1、R2、R3和R4四个桥臂的电阻值发生变化，引起电桥电压的改变。输出的电压为：

式中：k为应变片灵敏度系数；R1、R2、R3、R4为电阻阻值；Ui为供电电压。

灵敏度为输出电压于供电电压比值，其计算式如下：

式中，K为传感器灵敏度。

2.3 理论求解

根据传感器力学分析所得最大应变位置，利用WorkBench有限元软件中以path方式输出应变最大处的应变值，并结合应变片应变栅长度为1.1 mm选取11个点进行求解。在选择点时，应满足该区域应变变化平稳且在应变栅感应值最大。结果如表1所示。

该区域的数值满足应变片的要求，对该组数据采用复合梯形公式对其进行处理，将区间[a，b]划分为n等份，分点xk=a+kh，其中，h=(b-a)/n,k= 0，1，…，n，在每个子区间[xk，xk+1] (k= 0，1，2，…，n-1)采用梯形公式进行处理，其表达式如下：

以表1中R1数据为例，对区间[0，1]进行10等分，h= 0.1，k= 0，1，2，…，10，在每个子区间上采用复合梯形公式计算，结果示于表2。

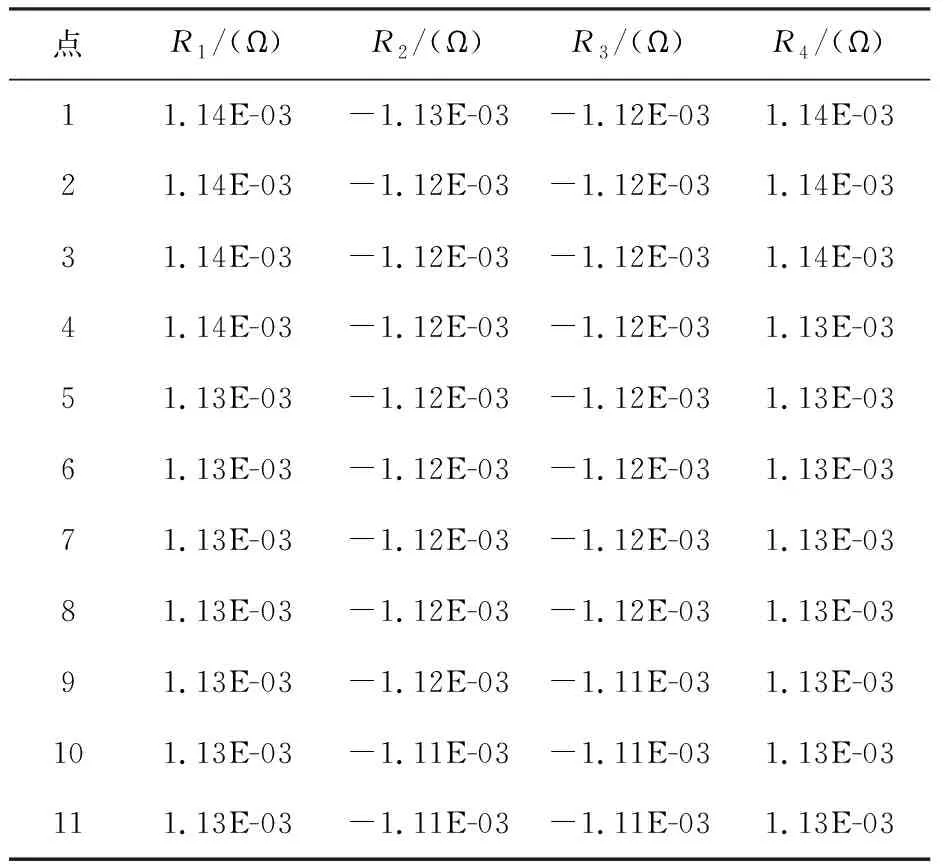
表1 符合应变栅要求数组

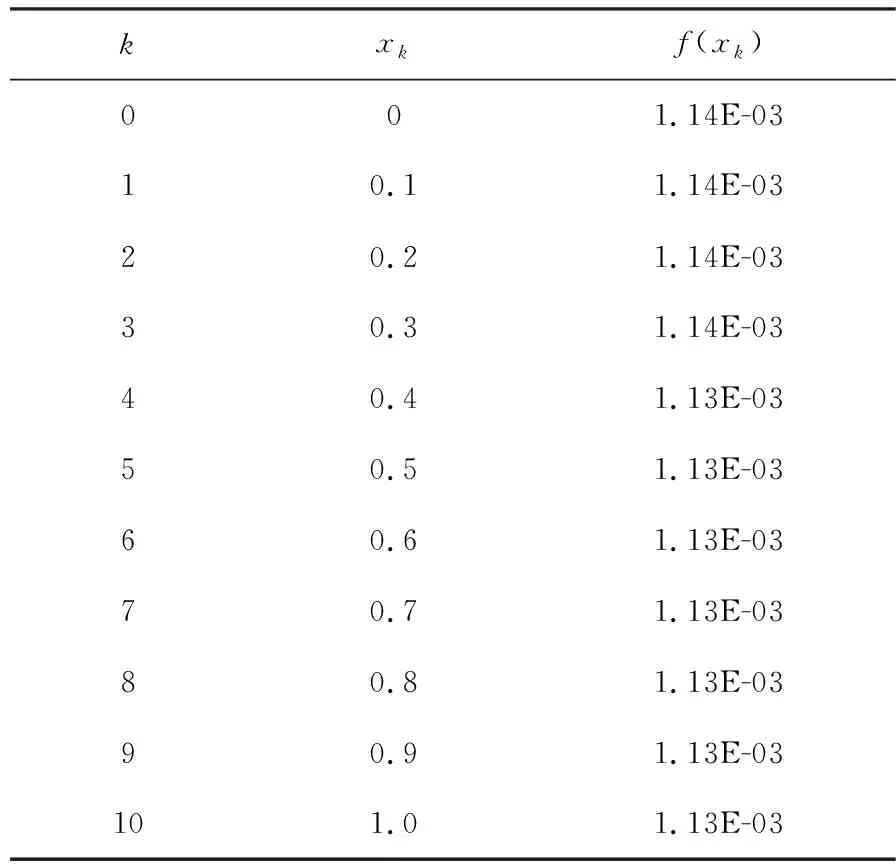
表2 R1处理数据

将表2中的f(0)到f(1)代入到复合梯形公式(3)得T10=0.000356。通过复合梯形公式计算得到总的应变量，根据平均值公式有：

根据计算R1方法同样可以求得R2、R3和R4平均应变量和总应变量，如表3所示。

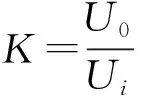
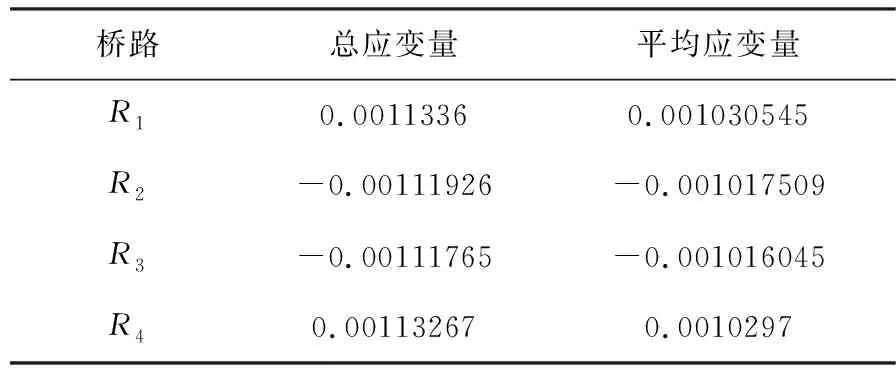
表3 各桥路的应变量

3 拓扑优化

3.1 拓扑优化理论

拓扑优化设计时需要考虑三个要素，即设计变量、目标函数和约束条件[9-10]。设计变量是通过参量变化来得到优化的参数；目标函数与设计变量相关，要求设计性能最优；约束条件是对设计进行限制，是对设计变量和其他性能的要求[11]。采用的模型为OptiStruct优化属性模型，可表述为：

式中，X=(x1,x2,…,xn)是设计变量，f(X)是目标函数，g(X)和h(X)是需要进行约束设计的响应函数。

3.2 软件优化设置

在WorkBench有限元软件拓扑优化模块下对电阻式应变传感器优化设置如下：

1)设计变量：以传感器结构为设计变量，结合有限元计算结果指定设计变量区域。

2)目标函数：以传感器应变增大为目标，利用WorkBench软件进行拓扑优化。不能直接以应力、应变为优化目标，而以质量最小、结构合理性等为优化目标函数。

3)约束条件：以质量减少50%和最大应力不超过材料的许用应力为约束条件进行设置。

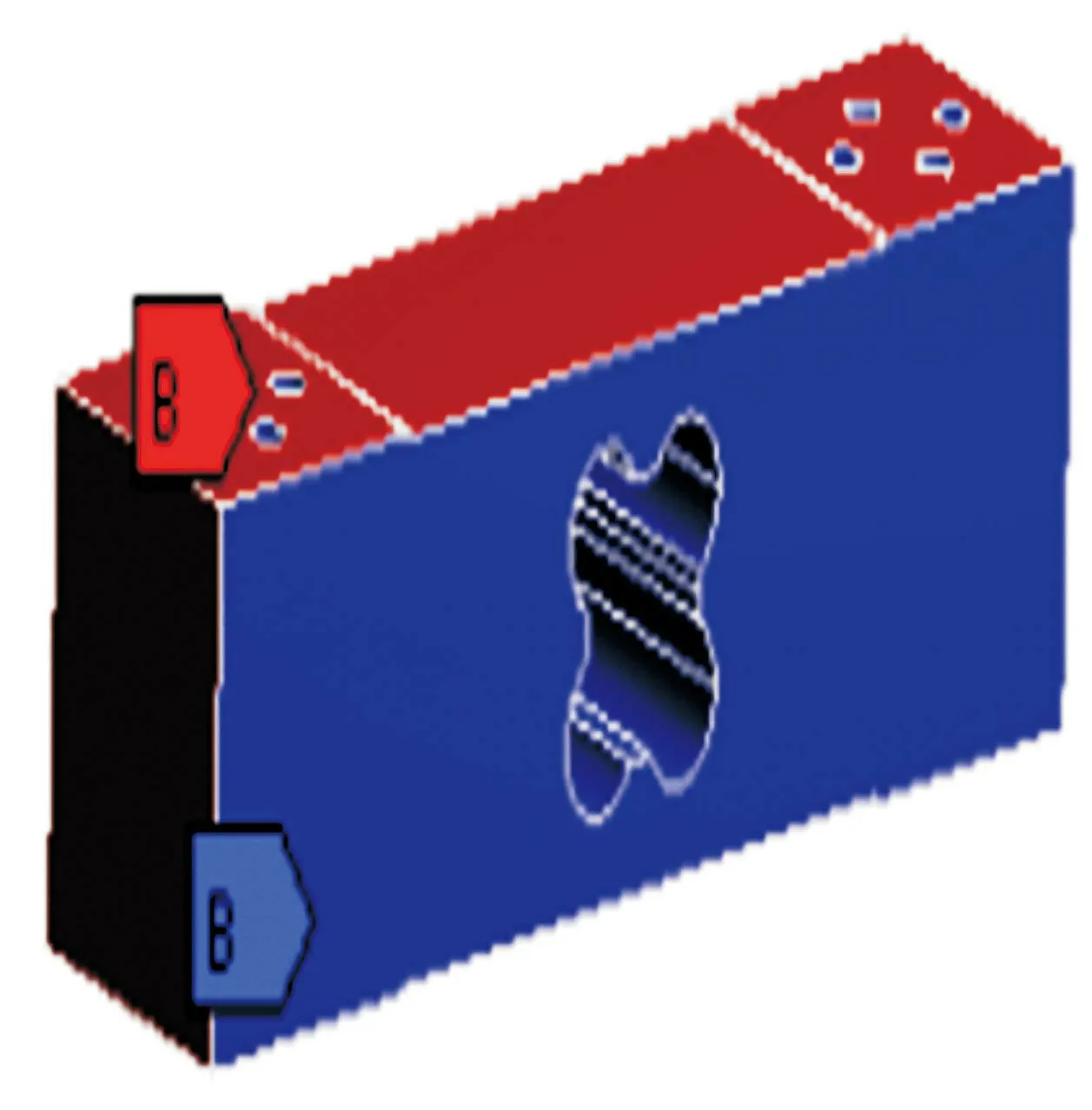
图8拓扑优化设置图

根据上述拓扑优化三要素在WorkBench有限元软件中进行相应设置，如图8所示。图8中B为优化区域和约束区域(蓝色区域B(前表面)为优化区域在拓扑优化中可变化的区域，红色区域B(上表面)为约束区域在拓扑优化中不能改变的区域)。

3.3 优化结果分析

在WorkBench有限元软件中完成优化三要素设置之后，进行求解得到优化后传感器的结构，如图9。对拓扑优化后结构重新进行有限元分析得到应力分布云图，如图10所示。由图10可知，优化后结构的最大应力为330.39 MPa，比原有结构的最大应力提高了27.32 MPa。此外，且最大应力位置也发生了变化。

3.4 优化后灵敏度理论值

根据前面所得结果重新对拓扑优化后电阻式传感器结构进行有限元分析，最大应力和最大应变的位置区域发生改变。重新进行贴片区域的选择，并输出贴片区域应变大小，结果如表4所示。

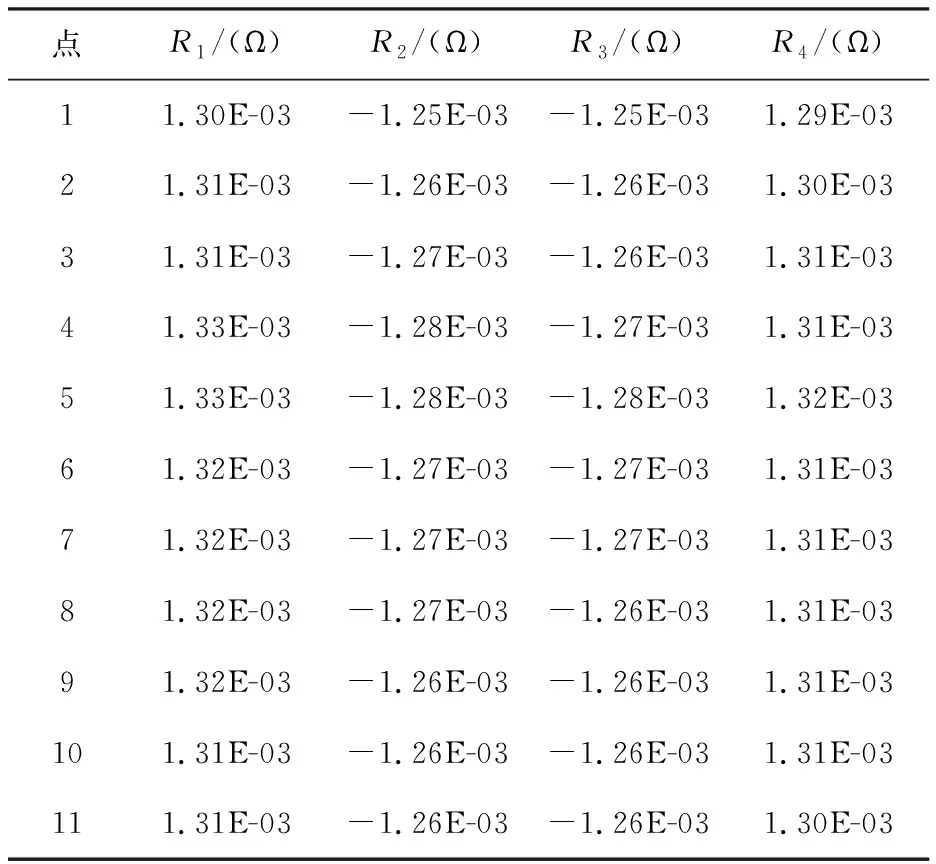
表4 优化后贴片区域应变大小

同样以R1贴片区域应变大小为例，采用复合梯形公式(3)可得T10=0.001317。通过复合梯形公式计算得到应变该数据总的应变量，根据公式(4)可得sum(R1)=0.00119。根据计算R1方法同样可以得到R2、R3和R4的平均应变量和总应变量，并根据公式(1)和(2)得到拓扑优化后灵敏度K= 2.57 mV/V。

4 结论

通过拓扑优化对电阻式应变传感器优化设计可以得出以下结论：

利用有限元软件求得电阻式应变传感器最大应力和最大位移，并结合传感器原理选择贴片区域。通过数值处理计算所得传感器灵敏度的理论值2.25 mV/V。

通过拓扑优化改变传感器的结构，其应力从303.07 MPa提高到330.39 MPa。并对拓扑优化后传感器的结构，重新计算其灵敏度为2.57 mV/V，原有结构传感器的灵敏度为2.25 mV/V，优化后灵敏度提高了14.2%，从而提高电阻式应变传感器的性能。