圆柱扰流非定常流动流场动力学模态分解

韦开君，吴 晴，刘立超

(中国电子科技集团公司第三十八研究所 浮空平台部，合肥 230088)

0 引言

圆柱扰流作为流体力学中的经典问题之一，在化工、建筑、水利、海洋等众多工程领域都有非常重大的研究意义。国内外学者通过实验和数值模拟的方法对圆柱扰流问题进行了大量研究，研究结果显示，尽管流体在经过圆柱后，会产生流动分离、涡脱落以及尾迹相互作用等一系列复杂的流动现象，但其基本特点是存在较为明确的涡脱落频率[1-2]。相比于常规基于时间历程的非定常流场分析方法，模态分解方法可以分辨出流场中存在的大尺度有序运动，更加直观地观察不同特征频率下的流动模式及其发展变化规律，特别适合用来描述圆柱扰流的非定常流动特征[3]。

2010年Schmid[4]首次将动力学模态分解(Dynamic Mode Decomposition，DMD)方法引入湍流研究，DMD方法已成功应用于分析各种流体力学问题，例如凹腔流动[5]、动失速尾流[6]、横向射流[7]、有限平板流动分离[8]、喷管流动分离[9]等。这表明DMD方法是探索复杂非稳态时空流场本质的成熟且有前途的工具。

Tissot等[10]对比了传统DMD和残差最小优化DMD方法对圆柱扰流尾迹PIV测试结果分析的影响。张宾等[11]和王智慧等[12]分别应用DMD对旋转圆柱扰流和椭圆柱扰流的PIV测试结果进行了研究。Stankiewicz等[13]采用DNS直接数值模拟方法对二维和三维圆柱扰流进行了仿真，并应用POD和DMD方法对仿真流场进行分析。Noack等[14]应用DNS方法对旋转圆柱扰流进行数值仿真，对比了传统DMD和递归DMD对仿真流场分析的影响。在实际工程应用中，PIV测试成本过高，而DNS数值模拟目前尚难以用于真正意义上的工程计算。因此，需要讨论采用工程上常用的湍流模型对圆柱扰流进行数值仿真，应用DMD方法进行流场分析的可行性。

本文基于SSTk-ω湍流模型，进行了圆柱扰流的非定常仿真，在时频分析的基础上，引入DMD方法对非定常流场进行分析，获取了各阶流场模态的频率及分布，提取了引起涡脱落的主导模态，并通过模态重构来分析圆柱扰流非定常流动的特征及变化规律。

1 动力学模态分解方法

对于一定时间和空间范围内的流场数据，在整个可用于分析的时间序列中，流场可表征为一系列离散时间步的“快照”组合(Snapshots) ，如图1所示。其中，第i个时间步的瞬时流场分布特性可用列向量vi表示：

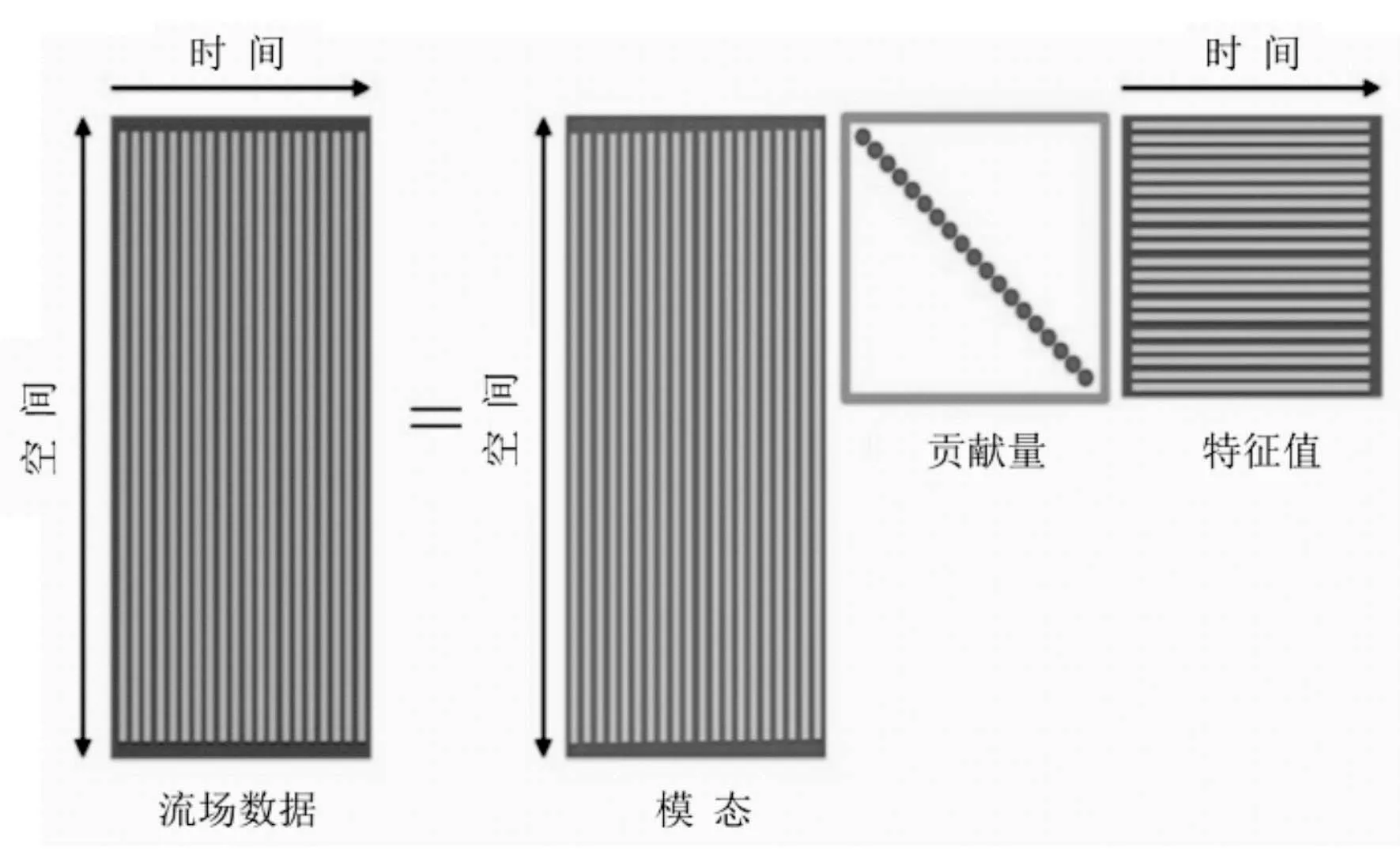
图1 流场动力学模态分解原理示意

vi=[u1,u2,…,um-1,um]T∈Rm(1)

式中：uj为j(j∈[1,m])节点上表征流场的物理量(压力、速度、或密度等)；m为流场的网格节点数量。

式中，n代表离散时间步，则矩阵的维数为m×n。

对流场做线性时不变假设，则可认为vi和vi+1存在线性Koopman映射[15]：

vi+1=Avi(3)

式中，矩阵A∈￡m×m，其特征向量反映了流场内各阶模态的空间结构，其特征值则反映了各阶模态对应的频率。因此，基于全局模态分解方法求解流场相干结构的关键在于求解矩阵A的特征值和特征向量。一般对于2000阶以下的中小矩阵，采用高斯法、QR法等直接方法即可求解。然而，对于一个复杂流场而言，其网格节点m通常远大于2000，而且矩阵A通常还是稀疏矩阵。对于此类矩阵，通常采用投影类算法，将高维矩阵投影至低维子空间，通过迭代计算其特征值和特征向量。

对于矩阵A和列向量v1，其张成的n维Krylov子空间为：

kn(A,v1)=span{v1,Av1,…,An-1v1}

=span{v1,v2,…,vn} (4)

对于矩阵A和列向量v2，其张成的n维Krylov子空间为：

kn(A,v2)=span{v2,Av2,…,An-1v2}

=span{v2,v3,…,vn+1} (5)

由式(4)和式(5)可知：

当n增加到一定数量时，可认为子空间基底存在线性相关，则有：

Vn+1=h1v1+h2v2+…+hnvn+r(7)

写成矩阵形式则有：

式中:r为残差向量;e为n阶单位向量，H∈Cn×n为上Hessenberg矩阵，具体可写为：

vi≈Uμi(10)

FDMD=U*AU(11)

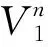
式中:Σ为r×r(r≤n) 的对角阵;U∈￡m×r;W∈￡n×r;星号代表矩阵的复共轭转置。将式(6)和(12)式带入式(11)中，则有：

则可直接对FDMD∈￡r×r进行特征值和特征向量求解：

FDMD=YΛY-1(14)

将POD基底空间上的特征向量Y投影回矩阵A，则流场的各阶动力学模态为：

Φ=UY(15)

与式(3)类似，在低维POD投影子空间内，有：

μi+1=FDMDμi(16)

将式(14)、式(15)和式(16)带入式(10)中，则可基于流场的各阶动力学模态对瞬时流场进行重构：

式中:向量φ为流场的各阶动力学模态;α表示各阶动力学模态的贡献量;λ为矩阵FDMD的各阶特征值，则整个时间序列的流场重构可写为如下形式：

将式(18)带入式(12)中，可采用GMRES求解得到diag{α}：

上述过程即为流场的动力学模态分解方法。

2 算例与分析

2.1 数值方法

基于二维数值计算模拟了圆柱绕流流场，计算几何模型如图2所示。圆柱模型的直径d=0.04 m，几何的坐标原点为圆柱圆心，坐标轴X方向为来流方向，进口距离轴心5d，出口距离轴心15d。计算域上下截面关于圆柱对称，距离轴心5d。

图2 计算域几何模型

数值计算采用结构化网格划分，网格总数为34.7万。入口边界条件为沿X方向速度入口，vx=0.15 m/s。出口边界条件为流出出口，出口压力为标准大气压。上下表面为滑移壁面，滑移速度的大小和方向和进口来流速度相同。圆柱边界为无滑移壁面。计算的流动介质为水，密度ρ=998.2 kg/m3，动力粘度系数μ=0.001003 Pa·s。本文计算的雷诺数Re=ρvxd/μ=5971，属于亚临界区。数值计算采用SSTk-ω湍流模型，边界层网格划分保证y+≤0.5。非定常计算时间步长为0.05 s，时间离散采用二阶隐式，空间离散采用二阶迎风，压力速度耦合算法采用SIMPLEC算法。计算域设置2个压力脉动监测点，分别位于距离圆柱后5d的正后方和下方2d处。

2.2 压力脉动时频分析

图3所示为某时刻卡门涡街分布情况。由图3可知，流体在给定的进口速度流向圆柱后，尾迹发生周期性涡脱落产生了交替的卡门涡街。

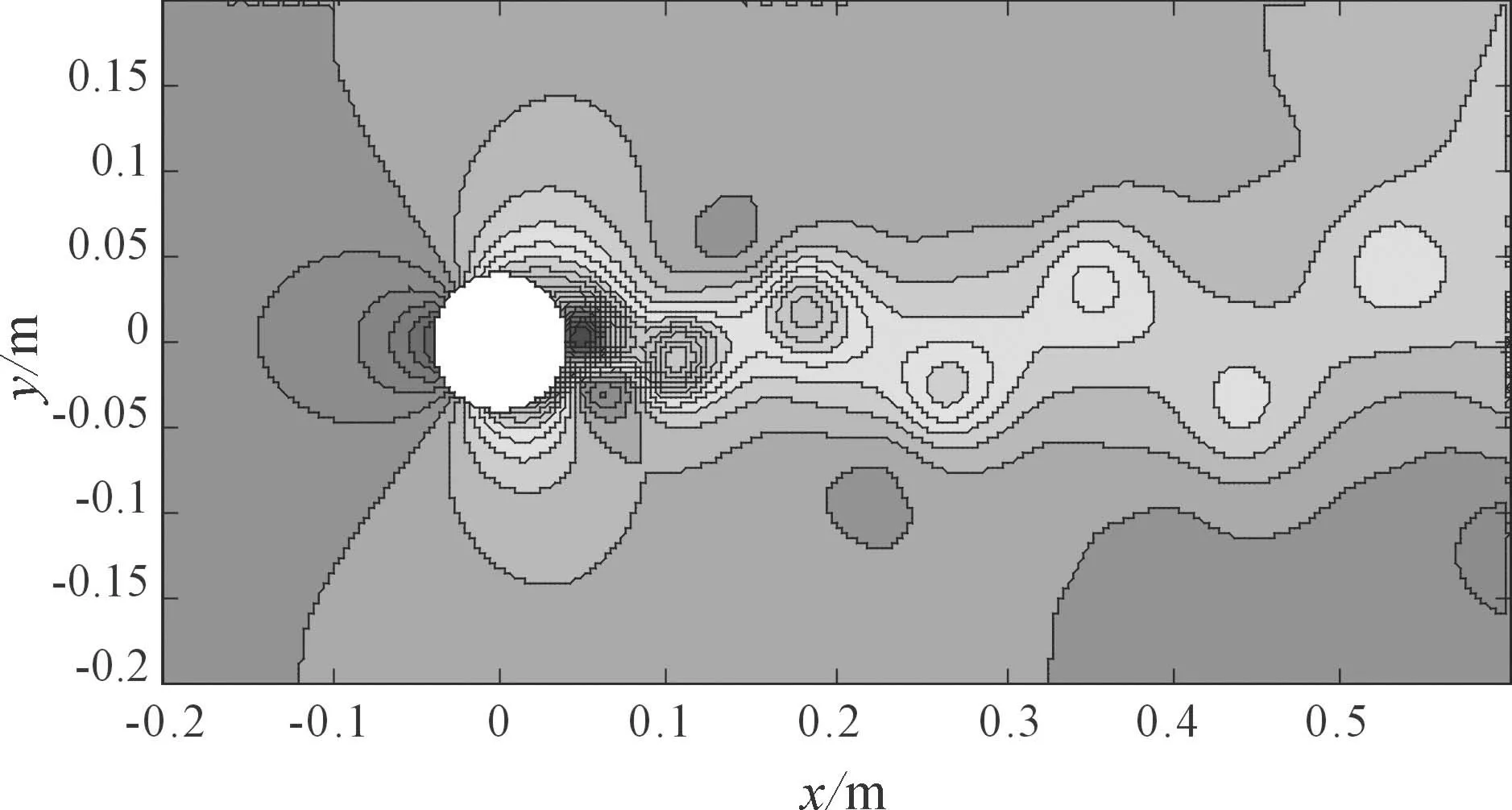
图3 卡门涡街分布

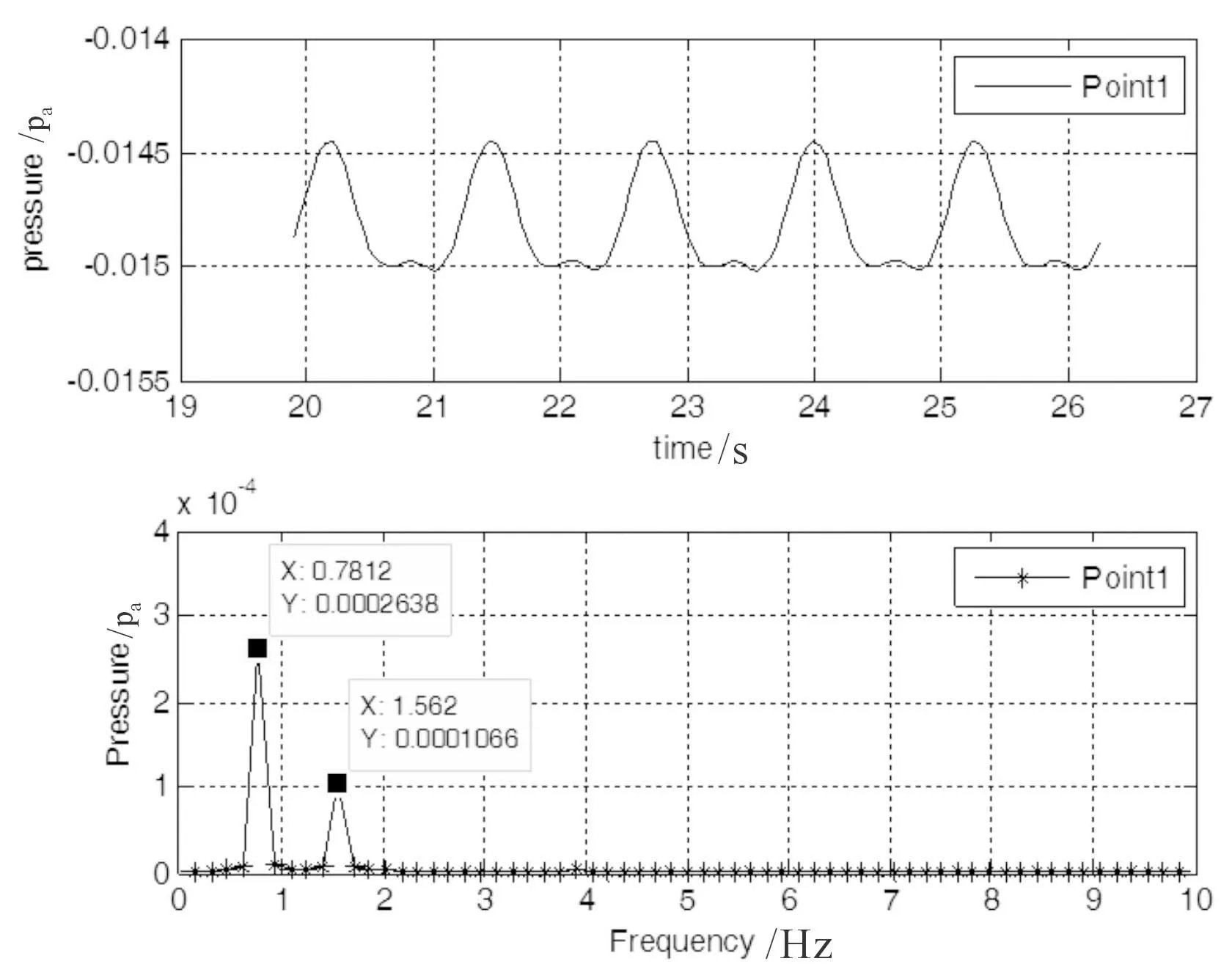
图4所示为监测点1的压力脉动时域分布和频域分布特征。可知圆柱绕流后涡脱落频率为0.7812 Hz。

图5所示为监测点2的压力脉动时域分布和频域分布特征。监测点2位于圆柱正后方，受到卡门涡街两侧涡脱落影响，其压力脉动频率为1.5620 Hz，是涡脱落频率的2倍频。

斯特劳哈尔数St是当地惯性力与迁移惯性力的比值，反映非定常流动的周期性[16]。针对圆柱后尾迹周期性涡脱落呈现的“卡门涡街”现象，可用St表示其周期特性。

式(20)中，f为涡脱落频率，d为圆柱直径，V0为来流速度。由前文分析可知，仿真计算得到的涡脱落频率f=0.7812 Hz，带入式计算得St=0.208。实验和计算结果表明，在 1500 ≤Re≤ 7200 范围内，基准圆柱的St数稳定在0.2～ 0.21之间。本文计算的雷诺数Re=5971，斯特劳哈尔数St=0.208，符合文献[17]给出的St数范围。

2.3 流场动力学模态分解

采用DMD方法对圆柱绕流流场进行分析，结果如图6所示。需要指出的是，DMD分解的第一阶模态为零频率模态，表示非定常流场的一个周期内的平均信息，图6给出的DMD分解结果为去除零频率模态后的结果。由图6可知，流场中存在2种非定常流动模态，1阶主模态频率为0.7863 Hz，2阶模态频率为1.5726 Hz。1阶模态是流动中最不稳定的模态，全局能量最大，其模态频率与前文时频分析中监测点1的压力脉动频率0.7812 Hz基本一致，该模态流动特征在圆柱扰流的非定常流动中占主导地位。2阶模态频率约为1阶模态频率的2倍频，与前文时频分析中监测点2的压力脉动频率1.562 Hz基本一致。

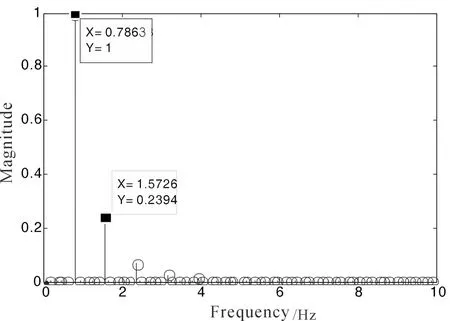
图6 流场标准动力学模态分解结果

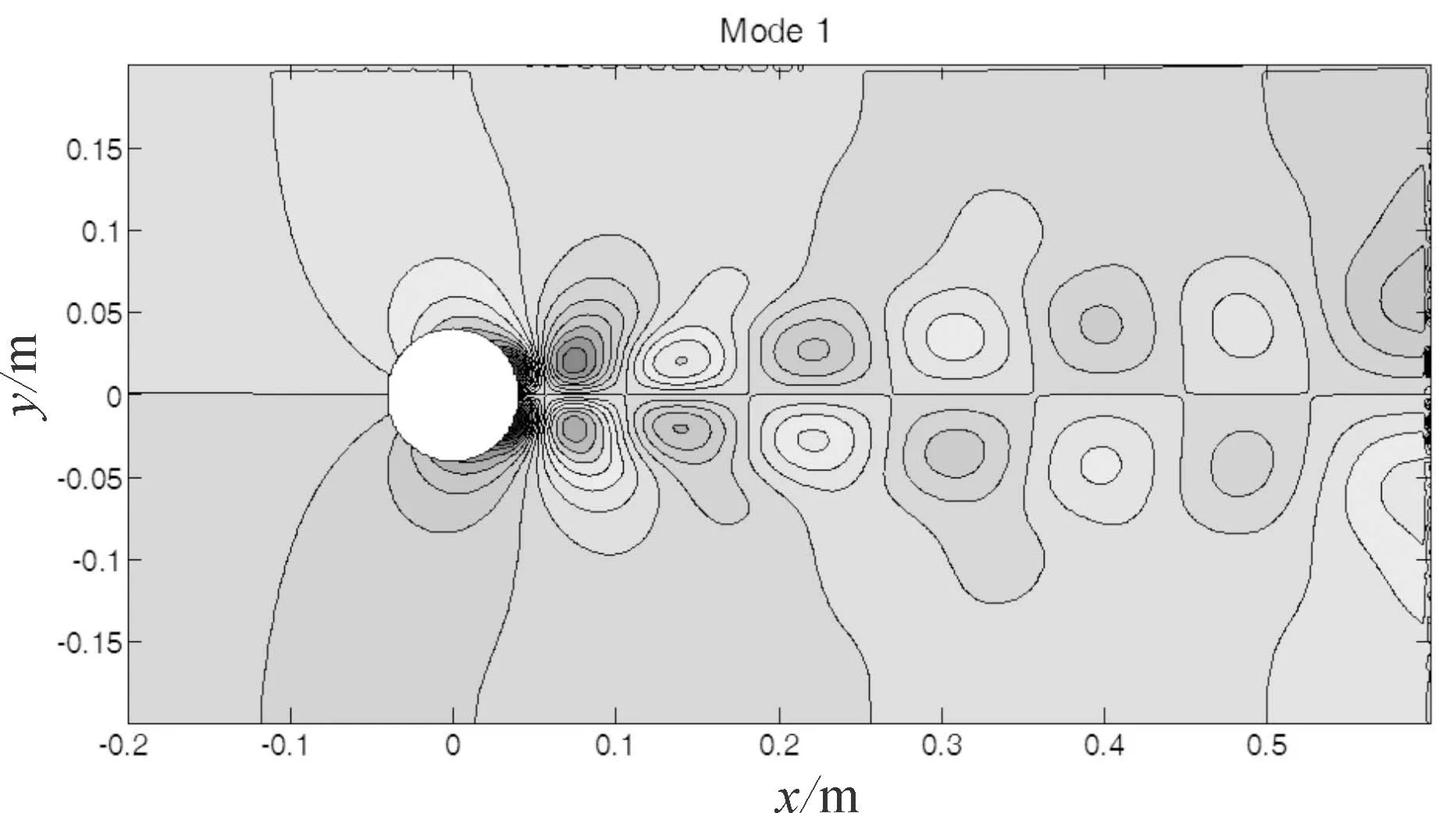
图7为经DMD分解的1阶和2阶流场压力分布特征。由图7可知，0.7863 Hz的1阶模态表现为流体经过圆柱后，在两侧形成周期性对称排列的旋转方向相反的双列涡线，即卡门涡街。1.5726 Hz的2阶模态主要表现为在圆柱正后方，对称排列旋向相反的双列涡线相互作用形成的类驻波特征。

3 结论

本文采用非定常数值仿真方法对圆柱扰流进行了研究，对流场内典型监测点进行了时频分析，并引入DMD方法对非定常流场进行分析，获取了各阶流场模态的频率及分布特征。主要结论如下：

(1)DMD方法可准确提取圆柱后方流场的振荡频率，与圆柱后方典型监测点的时频分析得到的频率吻合较好；

(2)去除零频率模态，DMD提取的1阶模态表现为圆柱后方两侧形成的双列涡脱落特征，2阶模态表现为两侧涡团在圆柱正后方相互作用形成的类驻波特征。

(3)DMD方法与CFD非定常计算相结合可以作为研究圆柱扰流非定常流动特征的有效工具，并推广至其他非定常流动问题的分析应用。