一种多主星模型的多视场星图识别方法

金 杰,谢俊峰,2,李 响

(1.辽宁工程技术大学测绘与地理科学学院,辽宁 阜新 123000；2.自然资源部国土卫星遥感应用中心,北京 100048)

1 引 言

星敏感器具有可靠性好、精度高、自主性强的优点,是高分辨率遥感卫星姿态控制的重要控件[1-3]。随着遥感卫星对无控制几何定位精度要求提升,甚高精度星敏重要性日益凸显[4]。对于甚高精度星敏感器而言,若想保证角分辨率足够高,对视场角的选取不宜过大,这样就导致星图中恒星的数量有限,当局部区域出现恒星数量过少,会对实时定姿的精度造成影响,无法提供准确的姿态信息。而多个星敏感器联合进行星图识别,可以使得这一问题得以解决,提高星图识别的可靠性,同时可以提高飞行器定姿精度[5-6]。高分七号是我国首颗亚米级立体测图卫星,于2019年11月3日发射,用于开展1∶1万立体测图[7]。星上采用两台国产双视场星敏感器,视场大小均为8.9°×8.9°,面阵大小为2048×2048像素,小视场、大面阵的星敏感器可以确保拥有较高的角分辨率,同时多个视场保证了星图识别的可靠性,为卫星提供高精度姿态数据。

目前绝大多数的星敏感器星图识别算法均采用的是单一星敏感器,对于单视场星敏感器而言,星图识别算法主要划分为两种类型[8-9],子图同构与模式识别。子图同构类算法主要是利用恒星的星等信息以及恒星之间计算出的角距信息,把恒星星点视为顶点,将恒星构成三角形或者多边形的模式,以此进行星图识别。其中经典算法有三角形算法[10-11]、匹配组算法[12-13]等。模式识别类算法本质就是对每颗恒星进行特征构造,生成一个唯一的特征“星模式”,利用这个“星模式”在导航星表中寻找相似导航星,其中经典算法有栅格算法[14]、基于统计特征的识别算法[15]。以上算法在用于多视场星敏感器的星图识别时,由于视场角较小,视场内的观测星数量不能得到保证,并且较小的视场角会对星特征的构建产生影响,因此,传统的基于单视场的星图识别算法不完全适用于多视场星敏感器。

针对多视场星敏感器星图识别方法研究的公开资料较少,尤政[16]等人公开了一种双视场星敏感器,射入两个视场的光线通过一个半透半反的平面镜,将光线进行透射以及反射,使其成像在同一个CCD上,利用光线之间的角度关系进行星图识别。这种方法仅适用于多视场观测星成像在同一星敏感器的情况下,并且光线经过透射与反射,势必会对观测星亮度造成影响。王昊京和吴亮[17]等人采用三角形算法优先对视场内恒星进行星图识别,若识别结果小于三颗星,才联合其他视场的恒星进行视场间星图识别。熊雪[1]等人以三视场为例,提出了一种多视场三角形星图识别算法,该算法采用图像拼接的方式,采用基于径向特征的方式,将同一时刻三个视场采集的星图进行拼接,生成一个广视场角的拼接后星图,对拼接后的星图进行三角形识别。该方法具有局限性,若多视场星敏感器光轴夹角较大,同一时刻生成的多帧星图无重叠图像,则无法完成对星图的配准与拼接。姜笛[18]等人提出了一种基于最优路径的多视场星图识别方法,该方法首先需要将星图进行融合,若不同视场生成的星图无重叠部分,同样无法进行星图的融合,因此,该方法也具有局限性。

通过以上分析,发现目前已有的多视场星图识别算法均对星敏感器之间的安装结构有着一定的要求,因此均存在着一定的局限性。因此,本文提出了一种多主星模型的多视场星敏感器星图识别方法,该方法不受视场间光轴夹角的限制,即使不同视场在同一时刻生成的星图无重叠部分,依旧可以对多视场联合进行星图识别,识别过程中,在利用星等信息的同时,引入距离信息构造出多主星模型,具有更高的可靠性。

2 多视场星矢量坐标转换

2.1 多视场星敏感器模型

多视场星敏感器可以在同一时刻拍摄不同天区的恒星,获得更多的恒星信息,覆盖区域更广,有效地解决了单视场星敏感器若想提高角分辨率,则必然需要舍弃观测星数量这一问题。同时,多视场获取的恒星位置更加分散,具有更高的稳定性与可靠性,求解的姿态信息精度更高。多视场成像原理如图1所示。

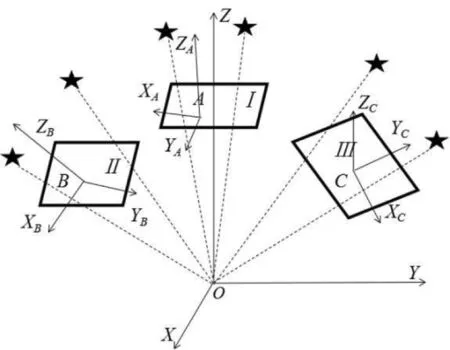
图1 多视场成像模型

2.2 星矢量坐标转换

多个星敏在同一时刻获得多帧不同的星图,经质心提取后,可以获得多帧星图中的恒星位于各自的像平面坐标系下的坐标。若想进行视场间星图识别,需要多帧星图中的星像坐标位于同一坐标系下,否则无法直接求取视场间恒星的角距信息,这里以一个星敏感器作为基准,设为1a,将其余星敏感器下的像点坐标转换到1a像平面坐标系下。

假设在某一时刻下,1a拍摄星图中某一恒星像点坐标为(Xa,Ya),利用式(1)将恒星像点坐标转换为空间坐标,并进行矢量化处理,其余视场恒星同理:

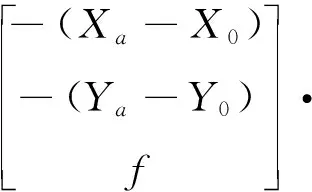
(1)

其中,(X0,Y0)为星敏感器透镜中心在像平面下的坐标;f为星敏感器透镜角距。

求得所有视场恒星在像空间坐标系下的矢量后,根据两个星敏感器之间的安装关系以及光轴夹角信息,可以求得矢量之间的旋转矩阵,将其余视场矢量左乘与1a视场的旋转矩阵,即可得到其余视场在1a坐标系下的矢量信息,如式(2)所示:

W12=A·W2

(2)

其中,A为旋转矩阵;W2为其余星敏感器坐标系下的恒星矢量;W12为其余视场恒星在1a坐标系下的恒星矢量信息。

3 多主星模型的多视场星图识别方法

本算法首先选取多个视场中的最亮星最为主星,通过匹配中心星概率的方法[19]对主星进行识别,即:计算主星与同一视场下其余所有星像点之间的星间角距,利用星间角距信息与导航星库中存储的角距值做对比,若角距差值小于匹配门限,则记录导航星信息,同时记录相同星号出现的次数,当完成匹配后,出现次数越多的星号越有可能是主星星号,由此得到多颗主星的主星候选星。主星确定后,选取主星中最亮的三颗星构成星等三角形模型。由于星等信息本身具有不稳定性,仅靠星等信息识别出来的结果的可靠性不好,而距离信息的可靠性强,因此,在构造星等三角形的基础上,再以距离信息,构造距离三角形,采用距离信息与星等信息联合的模式进行星图识别,使得识别结果具有更好的可靠性。多主星模型构造完成后,在主星模型的基础上,对其余副星(剩余未进行识别的星)进行识别。匹配识别的过程中,索引方式采用分段直线拟合的方法。

3.1 构建特征星库

特征星库作为星图识别的依据,对识别可靠性以及效率问题产生直接的影响,是星图识别中重要的一部分。多视场特征星库的构建方法与单视场有所不同,多视场存在视场间恒星识别以及视场内恒星识别。当进行视场内星图识别时,视场内星间角距值范围应为(0,FOV)。若两个星敏感器光轴之间夹角为θ,当进行视场间星图识别时,视场间星间角距值范围应为(θ-FOV,θ+FOV)。若按视场内特征星库的构建方法来构建视场间特征星库,则视场间特征星库会包含大量的冗余信息,给匹配识别效率造成很大的影响。因此,本文在构建视场间特征星库时,利用两个星敏感器之间的安装矩阵,以及星点信息估计视轴指向[20]。利用视轴指向定位天区。同时,为了减少特征星库大小,在构建时,只保留两个星序号信息以及角距信息,并且将求取的角距值扩大1×108,存储为整形。

3.2 匹配识别

1)确定主星。恒星的亮度信息是判断该恒星是否可以被星敏感器探测到的一个重要信息,原则上来说,在一帧星图中,越亮的星可靠性越高。因此,本文算法首先对每个视场中的恒星按照星等信息进行排序,选取视场中最亮的星作为待识别的主星。

2)主星匹配。计算主星与其余同一视场下所有星像点之间的星间角距,将角距值与星号信息保存。利用索引方式,将角距值与导航星库中存储的角距值进行匹配,若二者角距差值小于匹配门限,则记录导航星信息,并给予导航星一个标识count,初始值设定为0,用以记录该星号出现的次数。在匹配的过程中,同一导航星重复出现,则count加1。当完成匹配后,出现次数越多的星号,即设定的标识count值越大的星号,越有可能是主星星号,由此得到主星候选星。由于导航星库中存储的星间角距集数量较多,二分查找会导致匹配效率低下,并且星间角距与序号之间的关系并非是严格意义上的直线关系,k-vector查找法也不完全适合与多视场视场间恒星的匹配识别,因此,本文索引方式采用的是分段直线拟合的方法。

如图2所示,将星间角距组按照1°进行划分,然后分段对星间角距与序号的关系进行直线拟合,粗实线和虚线交替分别表示不同段。具体公式如(3)式所示,ai,bi分别表示第i段星间角距组的系数。基于拟合的结果,查寻结果更精确可靠。

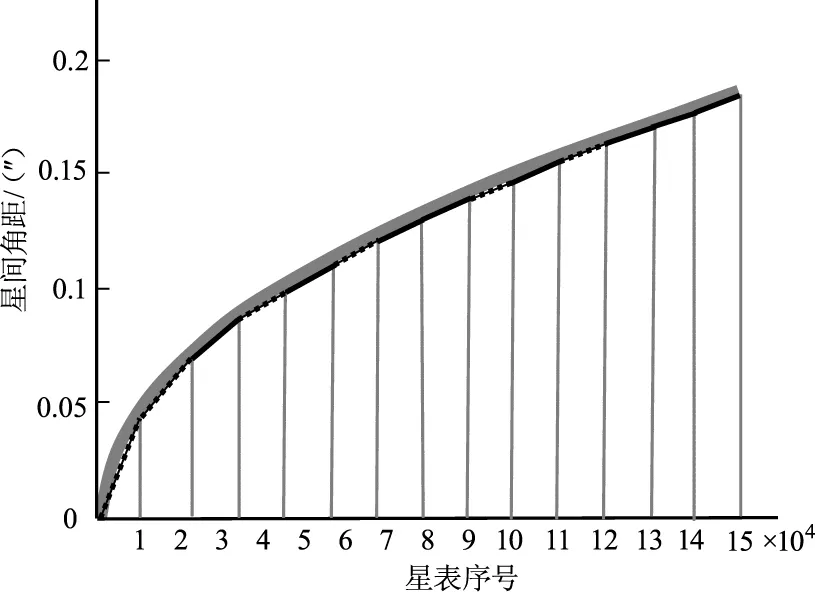
图2 星间角距与星表序号的关系

(3)

3)利用星等信息构建主星模型。若视场数为2,则以两颗主星为基准,构造星等三角形。选取除两颗主星以外的次亮星作为第三颗星,与主星候选星对组成三角形,生成候选星等三角形。若视场数大于2,则以最亮的三颗主星为基准,构造星等三角形。

4)利用距离信息,构造主星模型。构造距离三角形时,由于1a中恒星像点没有经过旋转矩阵的转换,因此以1a星敏感器中的主星为中心,确定两个半径R与r,在R于r之间选取距离中心星最近的两颗星,生成距离三角形。图3所示为视场数为2时,构造的主星模型示意图。其中,a与b为两颗主星,Δabc为星等三角形,Δade为距离三角形。若视场数大于2,星c应为第三个视场的主星。由此,则完成了阶段性星图识别。

5)副星识别。将剩余的所有副星分别与已识别的星相连,计算星像点角距,将满足与已识别星星间角距差值小于匹配门限的星视为候选星,记录下所有的候选星星对信息,若满足星序号限制条件,则认为是正确的匹配结果,索引方法同样采用分段拟合查找法。副星匹配示意图如图4所示。

图3 构造多主星模型

图4 副星匹配流程图

4 实验分析与验证

4.1 实验条件

基于现有算法进行分析和归纳,选用目前识别率与可靠性较高的基于匹配概率中心星的星图识别算法[19]与李葆华等人[21]的一种将角距和作为特征进行识别的多视场星敏感器的星图识别算法作为对比,利用高分七号在轨测试数据分别对这两种算法和本文提出算法的识别性能以及识别效率进行实验对比分析。

实验采取的基本星表为Hipparocs,主要用到的信息有星序号、赤经、赤纬以及星等信息。高分七号配备的星敏感器视场大小为8.9°×8.9°,面阵大小为2048×2048像素,星等选取的范围为(0,6.5),共8669颗星,剔除双星以及变星后,剩余8450颗星构成基本星表,实验数据选取高分七号星敏感器下传的星图数据,共计十轨,2141帧星图。图5为高分七号星图数据。

图5 高分七号星图数据

4.2 实验结果与分析

4.2.1 识别结果正确性验证

为了确定本文算法星图识别结果的正确性,利用十轨数据的星图识别结果分别计算拍摄时刻星敏感器的姿态信息。以768轨数据为例,给出定姿结果。姿态四元数如图6所示,横轴为星图帧数,纵轴代表四元数q值,q0为标量,q1～q3为矢量。

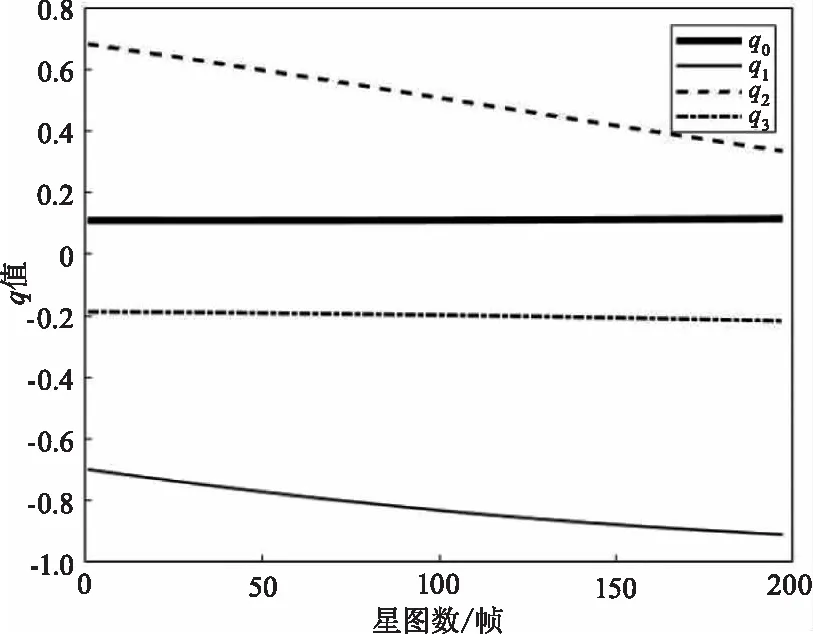
图6 姿态四元数

4.2.2 识别率对比及分析

对选取的十轨高分七号在轨测试星图数据分别采用基于匹配概率中心星的星图识别算法、李葆华等人提出多视场星图识别算法及本文提出的算法进行星图识别,三种算法的识别率如图7所示,其中横坐标为轨道号,纵坐标代表识别率。实验共计2141帧星图,其中,本文算法正确识别的星图数为2133帧,识别率达到99.6 %。

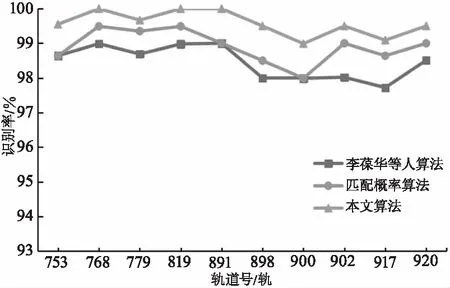
图7 识别率对比

通过对三种算法识别率的对比,在十轨数据的对比实验中,三种算法中本文算法识别率最高。对三种算法识别结果逐帧星图进行分析比较,在三种算法均成功识别的前提下,本文算法识别出的星数目更多,可靠性更高。

为了探究影响多视场算法识别率的因素,从10轨数据中选取一轨数据进行深入分析。以2019年12月24日拍摄的768轨数据为例,该轨共198帧星图,其中,以第3帧星图为例,多视场三种算法识别的结果如表1、表2、表3所示。

表1 本文算法识别结果

表2 匹配概率中心星算法识别结果

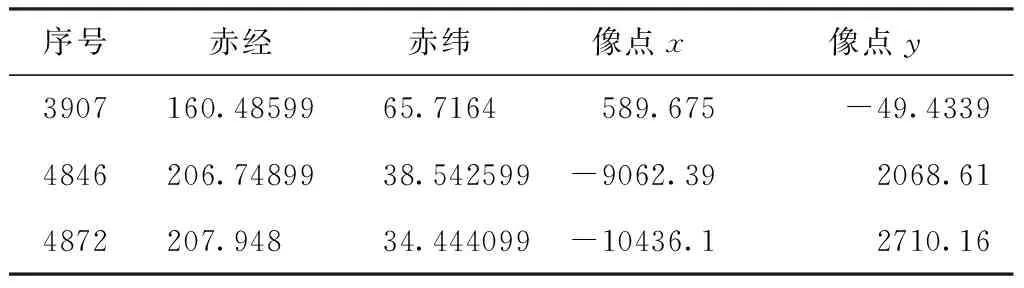
表3 文献[21]算法识别结果

由表1、表2、表3结果可知,本文算法成功识别的星为11颗,匹配概率中心星算法成功识别的星为7颗,李葆华等人算法只识别出三颗主星,本文算法识别效果更好。三种算法均选用最亮星作为主星,最亮星为1b视场中的星,转换后的像点为-10436.1,2710.16,成功识别后对应的导航星库中的星号为4872。在此基础上,本文算法选取的另一颗主星为1a视场中的最亮星,像点为589.675,-49.4339,成功识别后对应的导航星库中的星号为3907。以星等为特征构建星等三角形,三颗星号分别为4872,、3907与4846,以距离作为特征构建的三角形三颗星号分别为3907、3841、3846。该帧星图中,出现了主星过亮的情况,即当星的亮度达到一定程度后,星等信息反而会对识别结果造成负面的影响,同时,针对高分七号数据来说,当星过亮时,星图数据会出现亮点灰度值饱和现象,也会对星图识别结果造成影响。匹配概率算法以及李葆华等人算法均仅在此最亮星的基础上进行其余副星识别,这是造成星图识别结果不理想的主要原因。而李葆华等人算法三颗主星均为按照星等亮度选取的,因此造成了识别星数量低于匹配概率算法。同时,导致匹配概率算法以及李葆华等人算法识别失败的原因,也同样是此因素导致。而本文算法在引入星等信息的同时,又引入了距离信息,因此更好地保证了识别率。

5 结 论

本文针对目前已有多视场算法的局限性,提出了一种多主星模型的多视场星图识别方法。该方法利用星敏感器之间的安装关系,将其他视场星敏感器探测到的星点转换到基准坐标系下的矢量,使得多个视场内的星点信息可以联合进行识别。在匹配识别的过程中,提出了引入星等信息的同时,加入距离信息的模式,使得本文方法具有更高的恒星识别率,根据实验结果来看,本文所提出的星图识别方法识别率达到99.6 %,具有更好的可靠性。