基于网络结构的增强社会群体凝聚力策略研究

芶 欣,李欣悦,陈 武，刘佳谋

(1. 西南大学 计算机与信息科学学院，重庆 400715； 2. 奥克兰大学 计算机科学学院，奥克兰 1010)

0 引言

一个社会群体由许多在共享环境中进行交互的社会参与者组成[1]。群体的产生、群体成员相互合作、社会习俗形成等社会群体动态行为的研究一直是计算机科学和人工智能的一个重要课题。在这些研究中，社会群体的一个本质特征体现在群体成员间具有互动模式。一个人在社会群体中的决策是与他人的决策相关联的[2]。社会影响在很大程度上是由社会互动模式引起的[3-4]。

本文遵循结构主义的传统，将一个社会群体视为一个社会网络，该网络由代表社会群体成员的节点及节点间的相互联系构成。通过网络拓扑结构来分析社会影响，也就是节点的位置由它们的链路结构来决定。本文的动机来源于以下三个方面。

首先， 社会影响主要是作为个体特征来进行研究的。现有大量的研究都集中于通过解决影响力最大化问题来寻找影响力最大的个体或者群体[5]。由于每个个体都想在自己所处的社会环境中发挥最大的影响力，因此，要了解所有群体成员同时做出决策时可能会产生什么样的影响全局的模式就显得非常重要。这种全局观点自然需要引入博弈论的思想，而这个主题到目前为止并未产生较为深入的研究。

其次，迄今为止对社会网络的研究集中在网络“分解”上，也就是将网络划分成集群以构成所谓的社区结构。然而，很少有关于“一体化”问题的研究，比如社会凝聚力等问题。社会凝聚力表示一个社会群体中的成员愿意保持团结的意愿，其对于群体中的合作以及习俗形成的研究有着广泛影响[5]。对此，一个问题将会自然而然地被提出，即什么样的网络拓扑结构会影响社会凝聚力？这个问题的答案可以作为增强社会群体凝聚力的基础。

最后，虽然许多关于社会网络的博弈论分析都集中在研究均衡或者最优结果上，但大多没有考虑到其对社会网络结构进行调整的干预机制。对网络拓扑结构的局部调整可能导致所有社会参与者的系列变化。因此，在对社会凝聚力等全局特性问题进行研究时，理解博弈论概念和网络结构的动态变化之间的关系是至关重要的[3]。

本文从以上三个视角考虑，并基于联盟结构形成的研究，探讨了增强一个社会群体凝聚力的策略。首先，本文研究了一个基于合作博弈的社会群体动态行为模型。参与者可以选择组成联盟(子群体)，并根据其所在的联盟获得相应的奖励。对个体的奖励被定义为个体在联盟中产生的局部影响力。其次，本文提出了影响力博弈模型，该模型将社会凝聚力定义为所有参与者选择留在同一联盟并达到均衡，并重点讨论了维持网络拓扑结构的条件，以保证达到这样的均衡状态。最后，本文探索潜在的干预机制，通过为社会网络增加新的链接，以改变其网络拓扑结构，使其社会凝聚力得到增强。本文提出了基于核心边缘的策略，并通过实验验证了其有效性。

1 相关工作

目前有许多对凝聚力进行研究的工作[6-8]。Beal等人通过元分析方法对群体凝聚力进行了研究[7]。Purohit等人通过一组静态的朋友/追随者网络结构特征来描述社会凝聚力[8]。然而，这些研究中很少有研究如何形成社会凝聚力。本文将使用合作博弈模型来研究如何形成一个稳定的、具有凝聚力的社会网络。在博弈论中，有许多关于如何分组使一个网络达到均衡的研究。Gharehshiran等人利用合作博弈理论设计了一个分布式动态联盟形成算法，其中节点自主决定加入哪个联盟，使其可行睡眠时间最大化[9]。Massin等人提出使用合作博弈的方法，在ad-hoc网络中形成稳定的联盟，以保证网络中的信息可以稳定的传输[10]。Apt等人提出了用一种抽象的方法，基于简单的合并和分割规则转换一组节点的分区，以形成稳定的联盟[11]。这些研究都使用博弈论的方法，致力于将网络分割成不同的联盟来达到均衡。本文基于联盟稳定性的研究，考虑通过局部修改网络结构来达到整体的均衡。

2 基本概念

将一个社会网络看作一个无权、无向图G=(V,E)，其中，V是所有节点的集合，E为所有无向边的集合。G中每一个节点v∈V都代表了社会网络中的一个个体。对于任意一条边{u,v}∈E，{u,v}表示节点u和v之间存在社会联系，简写为uv。对于G′⊆G，S为G′的节点集，对任意节点u∈S，u与S中其他节点的连边数是u在G′的度，记作degS(u)=|{v∈S|{u,v}∈E}|。

合作博弈可以用一个二元组CG=(U，f)表示，其中，U表示参与者(player)集合，f表示收益函数。在合作博弈中联盟结构的形成是以个人收益为基础的,通常认为个人(节点)收益会影响联盟的收益。因此，下面将对个人(单个节点)收益进行定义。

定义1在一个联盟C中，任意一个节点u在该联盟中获得的收益，表示为fC(u)。若u∈C，且C∈SC，那么节点u在联盟结构SC中的收益可表示为FSC(u)，且fC(u)=FSC(u)。

在一个网络中，一个稳定联盟结构的形成过程就是节点不断选择联盟加入的过程。一个稳定的联盟结构的形成，需要网络中每一个节点都不再改变它们选择加入的联盟。假设每一个节点都是自私的，那它们会希望获得更高的收益，因此会选择能获得更多收益的联盟加入。当一个联盟中所有节点所获得的收益都不低于他们加入其他联盟所获得的收益时，该联盟就不容易因为节点的离开而遭到破坏，从而形成一个稳定的联盟结构。

若存在一个联盟S∉SC，且S中的每一个节点在该联盟中所获得的收益都高于它们在在联盟结构SC中所获得的收益，那么其就有可能离开原来的联盟，共同形成一个比原来的联盟更稳定的新联盟S，从而使得原来的联盟结构SC被破坏。反之，若没有这样的S存在，那么原来的SC则可以得以保留[12]。

定义2在图G=(V,E)中，对于一个联盟结构SC，如果存在一个联盟S⊆V，S∉SC，对∀u∈S，有fS(u)>FSC(u)，那么就说S可以阻塞SC。

本文用阻塞来衡量当前网络中的联盟结构是否稳定。

定义3在图G中，如果没有联盟S∉SC可以阻塞SC，那么就说该联盟结构SC是核心稳定的。如果大联盟是核心稳定的，那么说G是具有凝聚力的。

在社会网络的研究中，节点的度往往是衡量节点影响力大小的重要因素[13-15]。社会网络中两个节点之间的连边表示它们之间存在的社会关系。一个节点如果有较多的邻居节点则表示其被认可的程度较高。反过来也反映出其对所在联盟有较强的影响力。

众所周知，社会网络中任何个体都希望自己得到的支持和信任比较高，这样才能在联盟中得到更多成员的信任并影响他们，从而提高自己在联盟中的影响力。而在一个社会网络中，当一个个体的影响力有所提升的时候，影响力将会给它带来更多的隐形的或直接的收益(如金钱、信誉、社会支持等等)，往往这样的收益都会通过经济效益得以体现。本文使用奖励rC(u) 来衡量节点u在当前联盟C中的影响力所带来的收益。同时，当一个节点加入一个联盟时需要支付一定的费用，用tC(u) 来表示。一个节点最终所获得的收益(也称为局部影响力)与其影响力所带来的奖励以及加入联盟时的花费都有关。节点的局部影响力定义如下：

定义4在联盟C中的一个节点u，它的局部影响力如式(1)所示。

fC(u)=rC(u)-tC(u)

(1)

•奖励rC(u)： 用于衡量节点u在联盟C中的影响力给其带来的收益。当一个联盟的大多数成员都与节点u有连边时，u在当前联盟C中的影响力是相对较高的。然而，再增加一些新邻居节点，它影响力的提升没有最开始那么明显。因此，本文对rC(u)进行了定义，如式(2)所示。

rC(u)=logdegC(u)

(2)

•花费tC(u)： 用于描述节点u加入联盟C所需支付的费用，这笔费用与联盟中节点的数量有关。如式(3)所示。

tC(u)=log |C|

(3)

定义5在图G上的影响力博弈是一个合作博弈，表示为Γ(G)=(V,θ)。其中，V表示所有参与者(节点)集合，θ：V×2V是收益函数，表示节点u的局部影响力，有θ(u,C)=fC(u)。

如果一个社会网络G在影响力博弈上是有凝聚力的，那么就说G具有社会凝聚力。

在一个社会网络中，总希望所有的节点可以自愿加入到大联盟中，从而使得整个网络具有社会凝聚力。为此，本文采用合作博弈模型来研究如何实现具有社会凝聚力的网络结构问题(achieve social cohesion structure，ASCS)。

3 方法

社会凝聚力的形成往往是基于社会群体中个体之间的合作。合作可以使个人的资源和技术被整合在一起，从而更快、更好地达到预期目标[12]。许多研究表明，相似的个体间更容易形成信任并紧密相连，以便整个社会团体可以更好地发展[16-17]。网络拓扑结构是影响网络社会凝聚力的重要因素。本文基于合作博弈模型，考虑利用潜在的干预机制，通过改变社会网络的拓扑逻辑结构，增强网络社会凝聚力。

在社会网络中，部分节点紧密相连，形成一个小群体，其中的任意两个节点之间都有边，所有的节点在该小群体中都有相同的影响力。在网络中，这样的群体不容易被外力分开，是相对稳定的。这样的群体在图论中称作“团”。

定义6一个完全子图c⊆G是图G的一个团。团c中所包含的节点数是团的大小，G中大小最大的团称作最大团，记作mc。

团是网络中常见的子群体。它们的存在有助于探讨网络结构对网络的社会凝聚力的影响。那么，什么样的网络结构才能促进社会网络的社会凝聚力形成?这是本文将要研究的一个内容。

核心/边缘(core-periphery，CP)结构是一种非常重要的网络结构，它能很好地描述网络中节点间的竞争与合作关系[18]。Borgatti和Everett指出，CP网络结构具有紧密连接的核心部分以及与核心紧密连接但内部连接稀疏的边缘部分[18-19]。前人研究指出，网络的核心可以促进整个网络的稳定，帮助整个网络适应环境的波动。网络中核心节点之间的紧密连接可以使它们相互支持，在紧急情况下可以相互替换，以保证网络的性能[18，20]。这种结构特点与本文所希望得到的具有较强稳定性的网络结构不谋而合。

定义7一个标准CP结构的网络G=(V,E)可以把其分为核心C(C≠∅)和边缘P(P≠∅)两个部分。其中C={v|∀u，v∈V且u≠v，vu∈E}，P={u|∀u,m∉C且u≠m,um∉E}

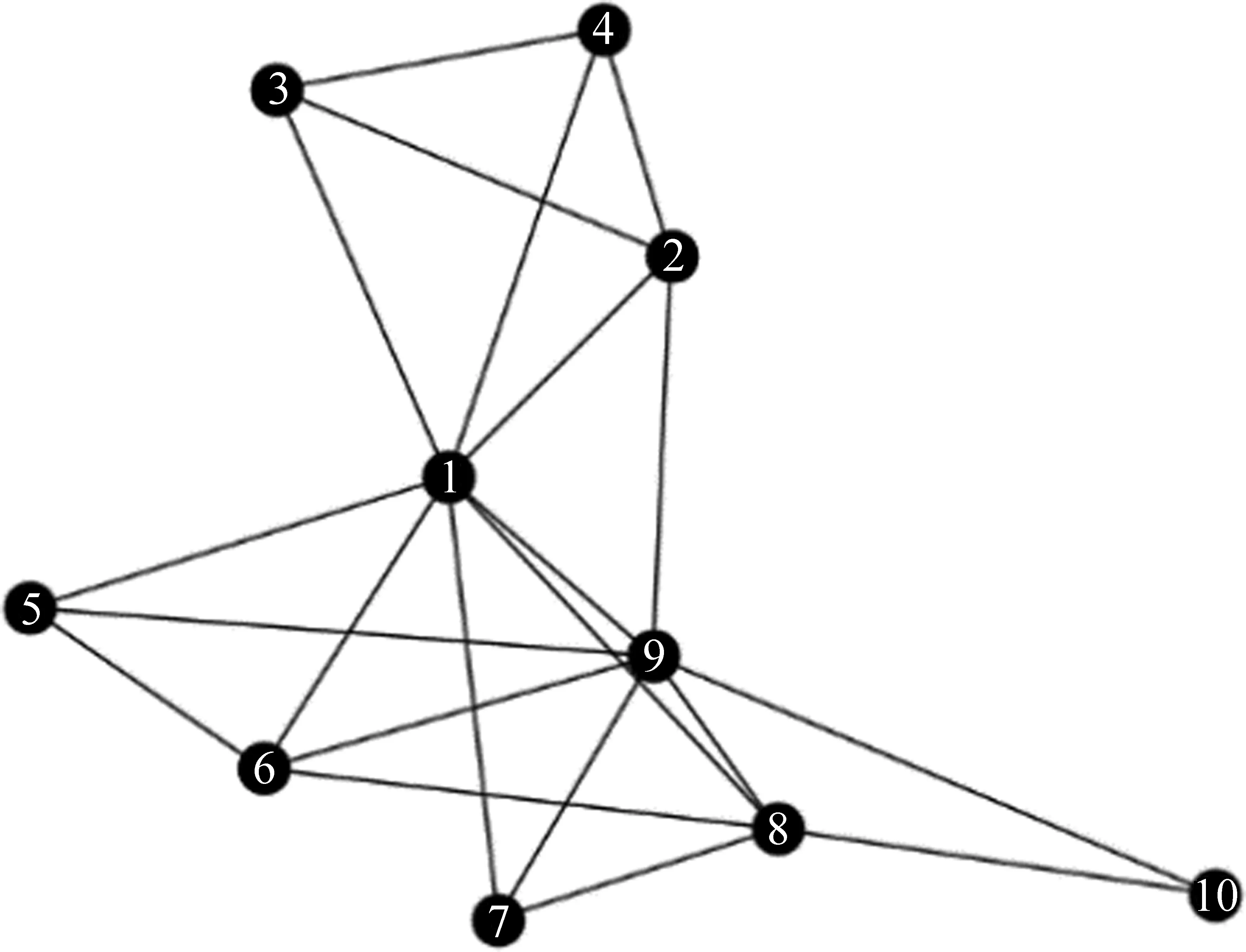
在一个标准CP结构的网络中，C部分的节点和网络中所有节点都有直接相连的边，P部分节点之间没有直接相连的边[19]，如图1所示，C={1,2,3,4}，P={5,6,7,8,9,10}。

图1 标准CP结构

在社会网络中，一些节点通常有相对多的邻居节点，这样的节点对网络的影响更大。这些节点的存在有利于将其他影响力较小的节点组合在一起，有利于网络的社会凝聚力的形成。我们发现核心/边缘结构的特征与社会网络中的上述特征具有相似性。因此，本文基于CP结构进行了一系列的研究。

定理1一个网络G=(V,E)，如果G是标准CP结构，那么G是具有社会凝聚力的。

证明： 若证明标准CP网络具有社会凝聚力，那么需证明在影响力博弈中不存在联盟S∉GC使得∀u∈S，有fS(u)>FGC(u)，如式(4)所示。

(4)

因为这是一个单调递增的函数，所以这等价于证明不存在联盟S∉GC使得∀u∈S，有：

(5)

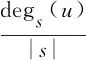
假设在一个标准CP结构的图G=(V,E)中，C部分节点数为m，P部分节点数为n。该图的联盟可以有以下三种情况： 联盟中所有的节点都属于C；联盟中所有的节点都属于P；联盟中一些节点属于C，另一些属于P，联盟仍是CP结构。在该图的大联盟GC中，对于 ∀v∈C都有收益，如式(6)所示。

(6)

对于∀u∈P都有收益，如式(7)所示。

(7)

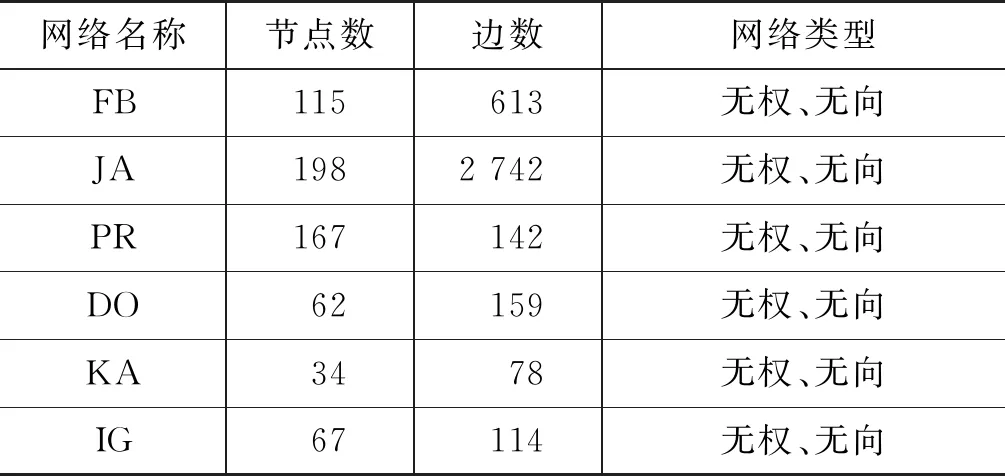
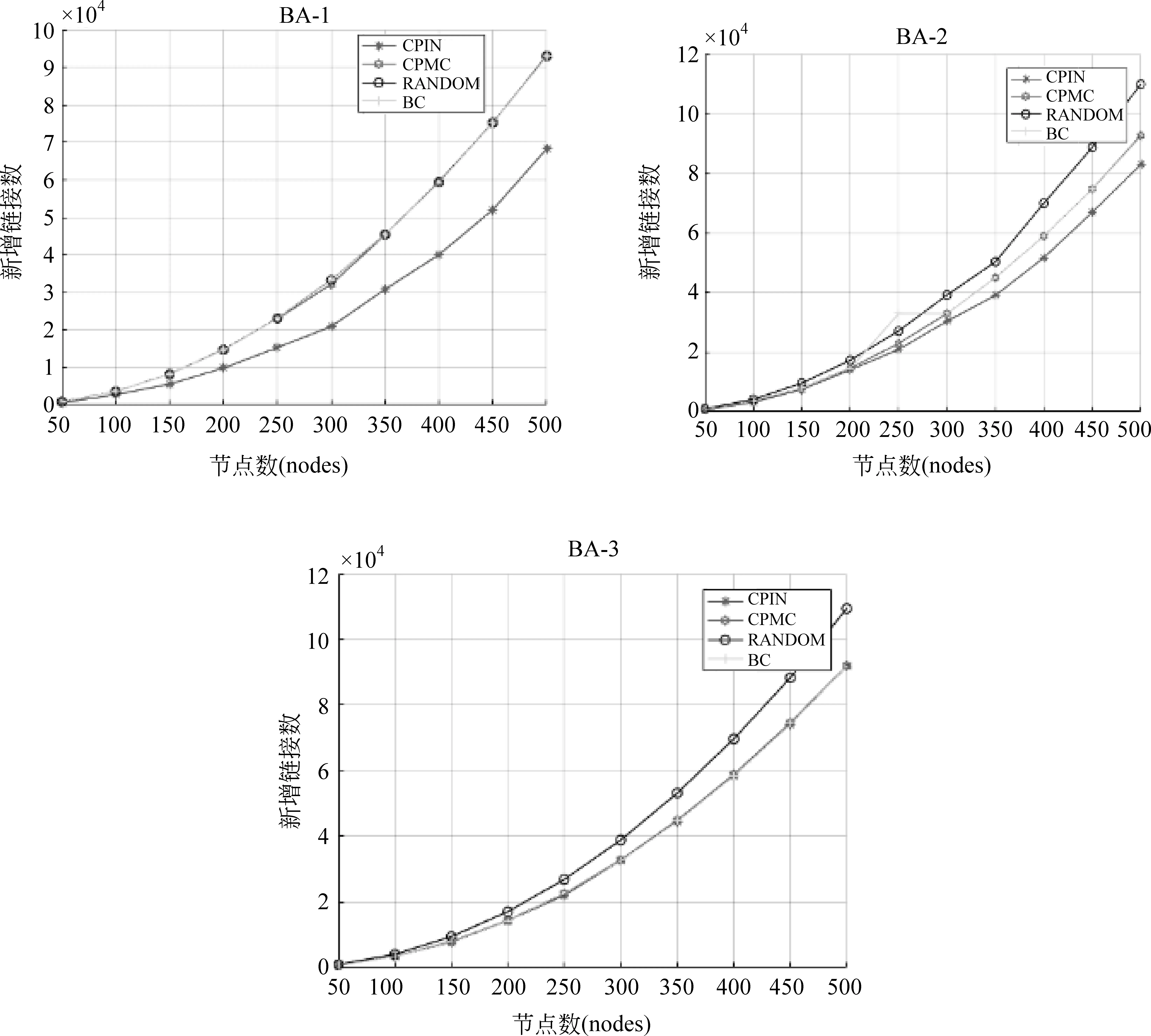
假设联盟S⊆V中所有的节点都属于P，即，∀u∈S且 ∀u∈P。那么，S中的任意节点u都有fS(u)=0，则fS(u)

假设联盟S中包含m1个C部分的节点，n1个P部分的节点，且S∉GC。那么，对于∀v∈S且v∈C，有：

(8)

在这种情况下，任意S均不可以阻塞大联盟GC。同时，证明了一个联盟S⊆V如果包含了C部分的节点，那么该联盟S一定不可以阻塞大联盟GC。

因此，可以证明任意联盟S都不可以阻塞大联盟GC。所以，任意一个标准CP图G是具有社会凝聚力的。

在许多情况下，一个网络很难达到标准CP结构，因为在边缘节点之间仍然存在一些连边。若一个网络G是基于标准CP结构的，且边缘节点之间仍有部分连边，那么我们将这样的网络称作近似标准CP的网络，简写为ACP。

定义8一个网络G=(V,E)是近似标准CP的网络，其分为核心C(C≠∅)和边缘P(P≠∅)，其中，C={v|∀u,v∈V且u≠v,vu∈E}，P={u|u∉C，∃m∉C且um∈E}，简写为ACP。

那么，在ACP结构的网络中C部分与P部分都要满足哪些条件才能使得网络G是具有社会凝聚力的网络结构？

在网络G中，节点u和节点v之间的最短路径记作dist(u,v)，节点u与其他节点之间的最大的最短路径为节点u的离心率，记作ec(u)=maxv∈Vdist(u,v)。若G中所有节点的离心率ec(u)不全相等，这样的网络称为non-diametrically uniform，记作NDU。若一个NDU网络G中所有节点的离心率ec(u)最大为2，则这个网络称作NDU2。LIU和WEI在文献[16]中研究了在图G=(V,E)上的合作博弈F(G)=(V,ρ)(popularity games)，其收益函数如式(9)所示。

(9)

同时，他们发现在popularity games中，网络G∈NDU2若满足定理2，则G具有凝聚力。

定理2在NDU2网络G中|V2|>c(c-1)，若|V1|≥(c-1)(|V2|-c)，那么G是具有凝聚力的。

其中，V1是与其他所有节点都有连边的节点集合，V2是除了V1以外的节点集合。c是V2所构成的子图中最大团的大小。

由此，在ACP图中可得到如下定理。

定理3在ACP图G=(V,E)中，mp为由边缘节点集P所构成的子图Gp的最大团。当且仅当|C|≥(|mp|-1)×(|P|-|mp|)且|P|>|mp|×(|mp|-1) 时，G具有社会凝聚力。

证明： 已知在ACP网络G中，C部分的节点与所有节点都有连边。

∀u1∈C，u2∈V且u2≠u1，有dist(u1,u2)=1。因此，∀u∈C，都有ec(u)=1。

易得，∀v1∈P，u∈C，有v1u=1；而∀v2∈P(v1≠v2)，dist(v1,v2)≤2,且∃v3，v4∈P有dist(v4,v3)=2。因此，∀v∈P，有ec(v)≤2。

由此可得，ACP⊆NDU2。

基于此，若证明网络G在影响力博弈中具有社会凝聚力。则需证明不存在S∉GC，使得∀u∈S，fS(u)>FGC(u)，如式(10)所示。

(10)

本文通过增加节点间的链接使所有的节点都愿意加入到大联盟中，从而使得一个网络具有社会凝聚力。在一个社会网络中，有部分节点是非常重要的，它们的存在可以促进一个网络社会凝聚力的形成。因此，本文提出了核心边缘算法，考虑将一个网络分为两层，分别是核心层与边缘层。其中核心部分由比较重要的节点组成，其他节点则构成了边缘层。通过增加核心部分节点与边缘部分节点之间的链接使得网络最终具有社会凝聚力。核心边缘算法的具体流程如图2所示。

图2 核心边缘算法流程

核心部分节点的选择是该算法的一个重点。网络中有一些节点可以成为链接整个网络的核心节点。在复杂网络的研究中，度是衡量网络节点中心度的重要指标。一般认为网络中节点的度越大，节点的重要性就越大[21]。然而，如果仅仅是用节点的度来对核心部分节点进行选择，那将忽略网络中个体与群体之间的关系，而个体与群体的关系是社会凝聚力形成中不可忽视的因素。往往一个具有凝聚力的群体可以带动更多的节点加入，从而使得整个网络具有凝聚力。本文从原始网络本身出发，考虑到任何一个网络原本必定存在一些群体，是由联系紧密的节点组成的，而群体之间的联系也是核心节点选择的考虑因素。本文结合这些测量指标和网络本身的特点，根据每次所选择节点数量的不同提出了两种寻找网络中核心节点的方法。在此基础上，提出了两种不同的算法来形成具有社会凝聚力的结构。

3.1 基于最大团的核心边缘算法(CPMC)

在网络中，往往希望核心部分节点之间是具有紧密连接的，若能找到原本连接就非常紧密的群体，那么是否就可以将这个本身连接紧密的群体作为核心层呢？然而一次性确定所有核心部分节点是非常困难的，因此本文考虑从连接紧密的最大团出发。团是完全子图，完全图是核心稳定的网络结构[16]。一个团是一个紧密相连的群体，最大团包含了更多能保持稳定的节点，若将最大团加入核心部分，那么既能保证核心部分的稳定性，也能尽快选择出核心部分节点。为此，本文首先提出了基于最大团的核心边缘算法(CPMC)来形成稳定的大联盟，从而使网络具有社会凝聚力。该算法使用迭代的方式，每一轮从边缘部分节点中选择出一个最大团加入到核心C部分，边缘P部分所构成的子图中最大团的所有节点同时添加到核心部分，然后增加核心部分(C部分)节点与边缘部分(P部分)节点之间的链接，并判断是否形成具有社会凝聚力的网络，若没有则重复以上步骤继续进行核心节点的选择，直到网络最终形成具有社会凝聚力的网络。该算法的详细介绍在算法一中给出。

算法一 基于最大团的核心边缘算法

CPMC算法可以快速得到一个明显的、稳定性较好的网络核心，因为它考虑了群体的特性。这种方法的缺点是可能导致在选择核心节点时没有考虑个体，为了更准确地选择核心部分的节点，应该将群体和个体的特性都加以考虑。对此，本文提出了CPIN算法。

3.2 基于重要节点的核心边缘算法(CPIN)

虽然最大团是一个非常稳定的群体，但对于整个社会网络而言并不是最大团中的所有节点都是核心的。为此，本文提出了另一种基于重要节点的核心边缘算法以促进社会网络中社会凝聚力形成。

在一个社会网络中，往往会存在多个最大团，有的节点可能属于多个最大团，这样的节点往往可以成为链接各个小群体的桥梁，也更有可能将整个网络紧密联系起来，使得网络具有社会凝聚力。本文将属于最多个最大团的节点称作重要节点。该算法同样使用迭代的方式，每一轮选择一个度最大的重要节点，将其加入到网络的核心部分，然后增加该节点与其他边缘部分节点的链接，每一轮结束时都要进行社会凝聚力的判断，如果没有形成社会凝聚力，那么将进行下一轮的重要节点的选择，直到最终形成具有社会凝聚力的网络。对于图3中的网络，可以很容易看出这个图的最大团的大小是4，其中包括了3个最大团，它们分别是{1,2,3,4}，{1,9,6,5}，{1,9,8,7}，可以看出节点1属于3个最大团，是属于最大团数目最多的节点。因此，考虑将节点1作为一个重要节点，并将它加入到核心部分。

图3 重要节点选择示例

在算法二中对该算法进行了详细的介绍。

算法二 基于重要节点的核心边缘算法

3.3 CPMC与CPIN区别

CPMC与CPIN均是基于核心边缘结构所提出的，但是选择核心节点的侧重点有所不同。具体来说，CMPC考虑到更快形成一个稳定的核心部分，从群体的核心稳定性出发，每次将核心稳定性较好的整个最大团的节点全部加入核心部分。而CPIN则是综合考虑群体和个体的关系，每次选择一个属于最多个最大团的节点加入核心部分。

4 实验和结果

为了验证算法的有效性，本文进行了一系列对比实验。降低由于新增链接所带来的成本是本文的一个目标。本文将使用随机算法(random)和介数中心性(betweenness centrality，BC)算法，与本文所提出的算法进行比较。在本文的仿真实验中，主要在无标度网络(BA)、富人俱乐部网络(rich-club,RC)两种合成图和6种现实网络中进行。使用四种算法在相同的网络中进行仿真实验，然后对比他们在相同网络中达到社会凝聚力所需要的花费(即，增加连接的数量)。

4.1 实验设置

本节将介绍本文在实验中所使用的现实数据集及合成图数据集。

为了验证所提出的算法的性能，本文在部分现实网络中进行了相关的比较实验，分别是： Football(FB)[23]、Jazz(JA)[24]、Prisons(PR)[25]、Dolphins(DO)[26]、Karate(KA)[26]和Italian Gangs(IG)。这些现实网络更有利于验证本文所提出方法的有效性。表1对现实网络数据集进行了详细介绍。

表1 现实网络数据集

4.2 实验结果

图4、图5分别展示了在富人俱乐部网络RC、BA网络中CPMC、CPIN、BC以及Random四种算法实现形成具有社会凝聚力的网络所需要的花费。其中，横坐标是合成网络中所使用网络的节点数目，纵坐标则表示形成具有社会凝聚力的网络所需的代价。图4是在Rich-Club合成图中进行实验的结果，可以看出本文所提出的CPIN算法具有较明显的优势，而CPMC与BC算法相比虽然有一定优势，但并不明显，同时也可以看出Random算法是所需花费最多的。图5是在BA合成网络中的实验结果，从结果可以看出它不仅有在RC中的实验结果的特点，同时也可以发现随着原始网络越来越密集，本文所提出的两种算法和BC算法所需的花费比较接近。

图4 RC网络中不同算法实现社会凝聚力所需花费

图5 BA网络中不同算法实现社会凝聚力所需的花费(增加链接数)

表2是在6个现实网络中进行实验的结果，从中可以看出CPMC与BC算法使得网络具有社会凝聚力所需的代价比较接近，而本文所提出的CPIN算法可以使用最小的代价使得网络具有社会凝聚力。

表2 在现实网络中不同算法实现社会凝聚力所需的花费(增加链接数)

续表

从以上分析可以看出，本文所提出的CPIN算法可以使网络在尽可能低的成本下实现社会凝聚力。同时，也可以看出CPIN算法能更准确地选择核心部分节点，有助于在社会凝聚力形成过程中降低花费。

5 总结和展望

本文提出使用一个合作博弈的模型从网络结构的角度来研究如何形成社会凝聚力。从理论上证明了标准的CP结构和满足一定条件的ACP结构是具有社会凝聚力的网络结构。这为研究如何实现社会凝聚力网络提供了重要依据。本文通过潜在的干预方法，提出了核心边缘的算法。通过增加网络中节点之间的联系，使网络具有社会凝聚力。实验验证了算法的有效性。下一步将探索具有社会凝聚力的更常见的网络结构，以及使用其他成本更低的方法来促进社会凝聚力的形成。