3-RPS并联机构基于任务空间的优化设计
马春生 尹晓秦 米文博 马振东
(中北大学机械工程学院,山西 太原 030051)
并联机器人相对于串联机器人拥有更好的刚度和承载力,而且运动性能优异[1],末端执行器可以获得很高的加速度和运动速度,有着越来广泛的应用[2-7]。并联机器人的优化对于弥补并联机构的缺点,有效利用并联机构的优点有着十分重要的意义[8]。但是大多数文章的研究对象为机构的工作空间[2-3, 9-10],忽视了机器人完成特定任务只利用了机器人可达空间的一部分,是机器人可达空间的子空间。因此对于特定任务的机器人应当根据任务确定和划分机器人任务空间为研究对象,分析机器人在不同机构参数下任务空间整体的性能变化。
而对于流水线上的机器人,尤其是以机械臂和末端执行器为结构的机器人,特别是流水线中的安装和拆卸等工序,其任务空间通常相似。而且随着可回收机械的发展,拆卸类机械器人已经成为人们研究的热点。因此本文以一种基于3-RPS并联机构的零件拆卸机器人为例,绘制机器人的性能图谱,研究机器人在不同的机构参数下机器人任务空间的体积变化和运动/力传递性能变化[11]。对机器人的设计参数进行优化,对于在流水线上工作,工作空间相似的机器人都有着指导意义。优化的流程如图1所示。

1 机构描述与应用
并联机器人的机构简图如图2a所示,由静平台,动平台和三条支链构成。静平台固结于机架,末端执行器与动平台相连,三条串联型的RPS支链连接了动平台和静平台(R——旋转副;P——移动副;S——球副),其中P副为驱动副。
在机器人工作时,机器人机体位于固定位置,机械臂面向流水线工作;而末端执行器工作时的位置移动主要涉及两个过程:移动末端执行器至目标零件处和将零件移入储物筐。如图2b所示,零件相对机械臂的位置具有一定的固定性,储物筐和机器人的位置相对固定。这就决定了机器人完成任务所需的工作空间并非整个机器人的工作空间,而是机器人可达空间的子空间。
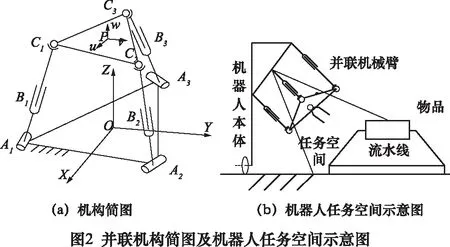
为了简化分析,可以将机器人任务空间转化为如图2b所示的圆锥形空间。锥形空间的中心轴线垂直于静平台,并经过静平台外接圆圆心。
2 运动学分析
如图2a所示,3-RPS并联机构拥有3个自由度,分别为绕X轴和Y轴的转动和沿着Z轴的移动[12-13]。

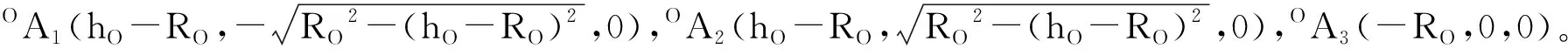
根据闭环矢量法[14]:
OCi=Ry(ψ)Rx(θ)PCi+P
(1)

因此,可以得到运动学逆解公式为:
(2)
其中,
3 任务空间分析
假设机构的杆li在移动副驱动长度为0时的长度为l;在实体模型中,机构的尺寸可以从0到无穷大,为了消除动静平台尺寸和杆长度对任务空间的影响,对机构的尺寸进行无量纲化[15],令:
所以:r1+r2+r3+r4+r5=5;为了简化机构的控制和分析,假设动平台的三角形和静平台三角形相似,则:
(4)
因此:
(1+λ)(r1+r2)+r3=5
(5)
由于等腰三角形的几何约束,则:r2<2r1;实际样机的制作中,动平台和静平台的比例不会过大或过小,因此假设λ∈[0.5,2],则可以得到参数的约束为:
(6)
所以,可以得到机构的设计参数空间如图4a所示。

当λ=2时,r1、r2、r3的取值范围在ADE平面上;当λ=0.5时,r1、r2、r3的取值范围在ABC平面上。因此,机构的参数在棱锥A-CDEB形成的空间内部取值。为了更直观地观察机构参数变化对机构性能的影响,将机构的参数映射到如图4b所示的二维平面内[16-17]。空间之间的映射方程为:
(7)
(8)
其中:
在机构设计参数空间中,分别对λ值不同的平面进行计算,结果如图5所示:
从图5a中我们可以看出,当r2确定时,r3增大,任务空间的体积成比例的增大;当r1、r2取最小值,r3取最大值的时候,机构的任务空间体积达到最大,即支链越长空间体积越大。从图5b~d可以看出,λ对机构任务空间的体积范围没有影响,但是随着λ的增大,机构其他参数的设计范围会减小。
4 运动/力传递性能分析
对于装配或拆卸机器人,拆卸速度是拆卸机器人的重要评价指标,而拆卸的机械臂的运动性能对于拆卸机器人的拆卸速度有着巨大的影响[18]。为了提高机械臂的运动性能,现利用以螺旋理论为基础的局部传递指标(local transmission index ,LTI)[19]和全局传递指标(global transmission index ,GTI)[2, 20-21]对机构进行分析和优化。
3-RPS并联机构的中的P副为主动副,则对应的3个单位传递力螺旋和3个单位输入运动旋量分别是:
(9)
式中:si为第i条RPS支链中,方向与P副的轴线重合单位向量,bi为原点O到A点的方向向量
因为P副的轴线经过R副和S副的轴线和中心,因此三条支链的输入传递指数(input transmission index ,ITI)ηITI i=1(i=1,2,3)。说明该机构在任何位形下输入端的运动都可以完全传入机构[19]。
利用式(10)可以求得对应于第i个传递力螺旋的输出运动旋量$Oi[19, 22]:
(10)
式中:$Ck为第i条支链的约束力子空间基底[19]。
则每个支链的输出端运动/力输出特性指标(output transmission index ,OTI)为:
(11)
支链的局部传递指标:
ηLTI=min{ηITI,ηOTI}=ηOTI
(12)
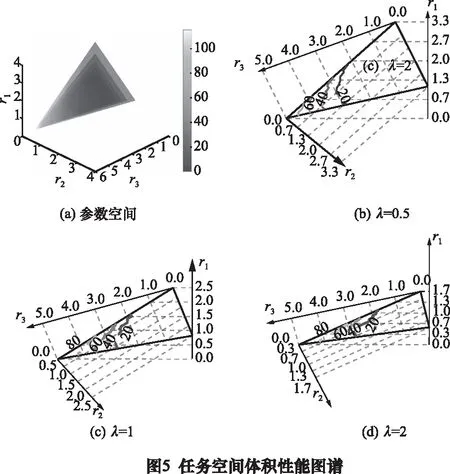
从图6中我们可以看到:
(1)当动平台的转动角度为0时,随着点靠近动静平台外接圆圆心的连线,局部传递指标随之增大,等高线呈同心圆形,如图6a所示。
(2)当动平台转动一定角度时,指定平面上的LTI会变小,最大点会产生有规律的偏移,当动平台绕X轴正向旋转时,LTI最大点会向Y轴负方向偏移;当动平台绕Y轴正向旋转时,LTI最大点会向X轴负方向偏移,反之亦然。
(3)当动平台转动一定角度时,会打破Z平面上LTI分布的各向同性,等高线呈同心三角形。顺着LTI最大点偏移的方向LTI下降最慢。
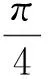
(5)旋转相同的角度,绕Y旋转会导致的LTI减小幅度大于绕X旋转导致的LTI减小幅度。
(6)λ的变化对各个Z平面的性能影响较小。
对于整个工作空间的评价,则使用全局传递指标(GTI)进行评价:
(13)
GTI随着机构参数的变化如图7所示:
从图7中我们可以看到,随着动静平台比例λ值的变化,任务空间的最佳运动/力传递性能区域的位置也在变化:r3一直处于约1.6。r2从2逐渐减小至1。r1从1减小至0.5,当λ=1时,最佳性能区域达到最大,最佳性能的区域紧邻任务空间体积为0的区域。任务空间体积的优化和运动/力性能的优化应当根据任务需要取得平衡。
5 结果
综上所述,可为3-RPS并联机构做出以下优化:
(1)任务空间体积和动力学性能不能同时达到最优,应在保证任务空间体积的情况下,设计参数应当尽量靠近GTI最大值。建议设计范围为:{0 (2)应当适当调整静平台和地面的夹角,在拆卸零件时,尽量减少动平台的转动。当无法避免转动时,尽量使末端执行器的工作范围为三角形,适当调整机构的静平台位置,使动平台处于性能最佳的位置。 (3)当动平台需要转动时,尽量使动平台绕底边上高所在的直线转动。 (4)根据静平台和地垄之间的距离,以及动平台需要转动的角度设计合适的支链长度。尽量使动平台的工作范围处于机构的高效工作区间内。 本文利用任务空间,局部传递指标(LTI),全局传递指标(GTI)为评价指标,绘制了机构的性能图谱,对机构的各个参数之间的比例,实体模型的大小进行了性能分析和优化。 (1)可以从全局观察到机构的性能和机构参数之间的变化关系,为机构参数的微调提供指导意义[23]。 (2)由于机构的对称性,机构在不同方向的转动对机构的运动性能产生影响,同时降低了垂直方向的动力学性能,应减少动平台的转动。 (3)对于3-RPS机构,转动时,使机构的转动轴线垂直于球副的球心之间的连线。 (4)应当根据任务空间的长度确定支链的长度,当动平台完成任务所需转动角度越大时,支链越长。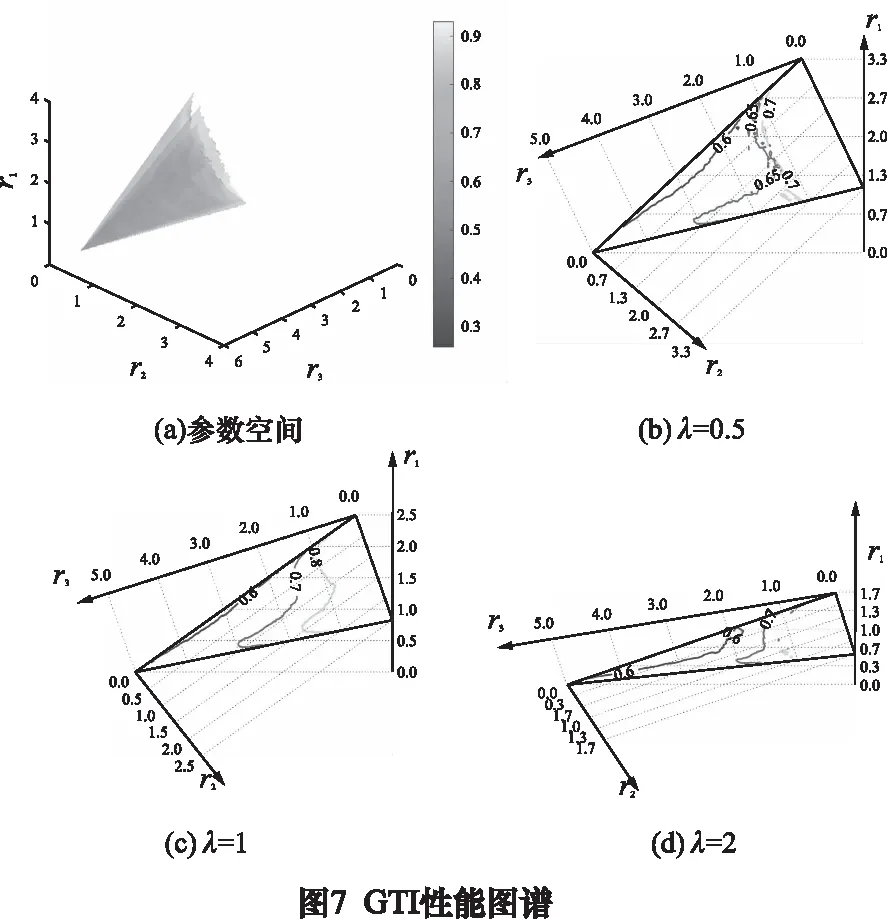
6 结语

