面向阵列抛光的叶片分组方法研究
王小东 罗贵敏 陈志同 朱正清 雷四雄 张海龙
(①中国航空规划设计研究总院有限公司,北京 100121;②中国航发南方工业有限公司,湖南 株洲 412002;③北京航空航天大学机械工程及自动化学院,北京 100191)
在航空发动机上,叶片制造工作量约占整台发动机制造工作量的25%~40%,叶片的生产进度直接影响整机的生产进度,加工效率尤为重要[1]。叶片的制造质量可直接影响发动机服役性能和寿命,普惠公司压气机部的大量实验研究发现,对于某些大型风扇叶片,叶片某些部位的参数0.025 4~0.076 2 m的加工误差会完全导致转子叶片服役性能和寿命的改变[2-3]。目前,国内主流叶片专用数控加工机床一次只能加工一个叶片,同步加工多叶片的多主轴叶片数控加工技术尚处于萌芽阶段。在保证加工精度的前提下,对多个叶片同时加工,就有希望成倍提高叶片的加工效率。德国斯塔玛(STAMA)公司制造了世界上第一台双主轴加工中心,与单主轴加工中心相比,节省了40%的耗电量,同时缩短了加工时间[4]。对于每件工件的成本,斯塔玛公司基于亚琛大学的研究指出最佳的情况发生在一次装夹4个工件时,也就是每个主轴在循环中加工2个工件,每个单元的成本可以降低到单主轴机床上加工同样4件工件的70%以下。德国CHIRON公司研制了双主轴和四主轴机床,其采用直线排列方式,并指出使用双主轴加工成本可以降低约40%,德国亚琛工业大学机床研究所(WZL)进一步研究论证了四主轴加工效率较单主轴提高250%以上[5]。北京航空航天大学将传统多主轴机床采用“直线阵列”排布工件改为以“矩阵阵列”排布工件,在同样机床空间下主轴数量可以从n→n×n,自主设计并研制了四轴五联动矩形阵列叶片全型面抛光机床[6-8]。该数控抛光设备具有3个移动轴X、Y、Z和2个转动轴B和C,回转工作台C回转角度为360°连续回转,主轴摆头B摆动角度为±45°,轮式抛光工具通过标准刀柄连接至4主轴,工件通过快换工装安装于回转工作台。
在航空发动机叶片抛光加工领域,超硬磨料轮式抛光工具已经实现多种型面叶片的数控抛光。但不可避免的是,尽管叶片在抛光前工序已经满足设计公差要求,但由于装卡定位、刀具切削力、切削热、残余应力、刀具磨损以及加工振动等因素会导致加工变形,不可避免地会产生加工误差[9-10]。为了减小叶片切削变形,Imani L[11]、Cai S[12]等对叶片加工时的切削力进行建模预测并进行了对应的误差补偿,以提高铣削加工的精度;孟凡军[13]等对叶片过定位产生的装夹变形进行了研究。由于批量叶片铣削后再抛光仍旧存在型面差异,最终的抛光合格率和效率会受到一定影响,工厂的传统做法是用样板法透光检测后按余量标记划线分组,再进行分批人工抛光。这种方法效率低,劳动强度大,且依赖工人的经验,质量不稳定。
目前对于大批量叶片的精密测量,航发厂为了配合生产加工的节拍,提高生产效率,多数已开始采用非接触扫描式测量获取测量数据,其中应用最广的是白光机扫描测量,其输出的数据是每个截面的位置偏差以及截面扭角偏差等变形特征数据。本文在目前发动机制造企业要求对铣削后抛光前每件叶片进行白光扫描测量的现状下,利用检测报告中的变形数据对批量叶片进行了分组,以保证组内叶片因加工变形产生的形状差异较小,以满足同步阵列高效率加工模式下获得更高的抛光质量。
1 基于变形特征的叶片分组方法
1.1 叶片铣削变形分析
在叶片铣削加工中,存在多种加工误差会导致叶片加工后产生变形,在原基准下余量分配不均的情况。主要表现为在叶片的不同截面会产生不同程度的弯扭变形、弦长偏差以及进排气边厚度偏差等,其中主要的叶片截面内的弯扭变形误差如图1所示。在实际生产加工了解到批次叶片主要的加工误差集中在叶片的弯扭变形,故本文主要针对叶片检测时常用的各截面弯扭变形量作为分组的指标。本文叶片依变形特征分组的主要流程如图2所示。


1.2 主成分分析法
主成分分析法可以将原来多个彼此相关的指标线性组合为少数几个彼此独立的综合指标,提取原全部指标的统计信息,多为方差。一个指标的方差越大,它就越能用来区别总体中的个体。一个指标的方差若等于零,该指标就不能用于区别个体。因此,综合指标按提取原多个指标的方差信息从多到少,依次称为第一主成分、第二主成分等。主成分分析的数学模型如下:
(1)
式中:Fk是k个主成分,Xp为初始指标。
(2)
式中:μjl为第j个指标对应于第l个主成分的初始因子载荷,λl为第l个主成分对应的特征值。
根据主成分表达式得出综合权重模型:
Y=b1X1+b2X2+…+bpXp
(3)
其中:
(4)
式中:θl为第l个主成分对应的方差贡献率,b1,b2,…,bp即每个指标的权重。
1.3 分组指标确定
从铣削叶片的测量报告中可获得多个截面的弯扭变形值,考虑到对于同一类弯曲或扭转变形的指标在不同截面上具有相关性,故可以利用主成分分析法对相关性强的指标进行缩减,选择出最具有代表性的指标。
主成分分析确定指标权重的主要思路是:通过主成分变换,建立用初始评价指标描述的新的主成分指标,这几个主成分相互独立,且包含了初始评价指标的大部分信息;再通过特征值与贡献率的计算确定每一主成分描述样本时所占的权重,建立用主成分描述样本的模型;最后将主成分的表达式代回模型,得出用初始指标描述样本的权重,建立用待评价指标描述样本的模型。其流程如图3所示。
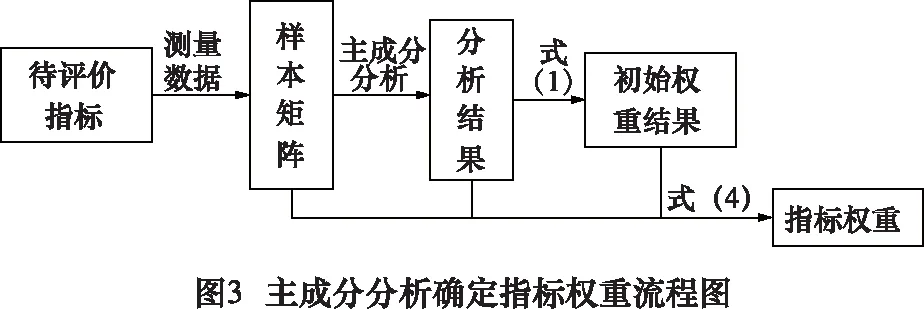
其主要步骤为:
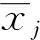
(5)
(2)求相关系数矩阵;
(3)求相关矩阵的特征值,特征向量与贡献率;
(4)计算各指标权重。
对于变形情况单一的,只是弯或扭的批次叶片,在确定了叶片指标的权重后,可以对影响叶片变形的众多指标依据权重进行排序,选出对批次叶片影响最大的一到三个指标作为最终的分组指标;在确定了指标后可以获取样本数据该指标的变化范围,依据后续工序的需要进行水平的划分,如二等分或三等分,这样对不同指标的不同水平进行正交组合就可以构成一个分组的划分表,如图4所示:
2 叶片分组实验
针对航空发动机厂里同一批次的压气机叶片进行分组实验,如图5所示。利用德国温泽CORE-DS五轴白光测量机对叶片的7个待检截面进行扫描测量,如图6所示。测量机采用白光点光源测头,测头在随测量机X、Y、Z轴移动的同时,也在按照叶片截面的矢量方向调整姿态,当叶片在转台上连续旋转360°后,截面测量完毕。


2.1 初始样本构成
整理提取叶片测量报告中的所有7个测量截面的3个变形特征:X、Y方向弯曲变形以及截面扭转变形,这7个截面的变形数据可以基本反映叶片叶身相对于理论数模的变形情况。获取到该批次的24个叶片,故有24个样本,每个样本由7×3=21个特征指标构成,最终构成一个24×21的初始矩阵。
2.2 叶片变形状态分析
依据组成的初始样本矩阵,做出该批次叶片基于测量基准的X、Y方向弯曲以及扭角随叶片截面变化的趋势图来分析该批次叶片在不同变形评价指标之间的一致性,如图7所示,图中每一条折线代表一个叶片随截面的指标变化情况:

从图7可以看出:这批叶片在叶盆叶背方向即Y方向变形在0~-0.12 mm范围内,比叶片进排气边方向即X向大(-0.02~0.04 mm),且这两种变形都是随截面沿积叠轴(Z轴)位置的升高在逐渐变大;扭角除了个别叶片外随截面的变化不大,且叶片间差异较小,变化范围基本在0~-0.15°,证明这批叶片整体扭角相对稳定。进一步的,为了观察叶片弯曲变形的波动性,用每个叶片每个截面的变形值减去所有叶片该截面该方向变形的平均值,去除系统误差后得到该批叶片X、Y两个方向的弯曲变形情况如图8所示。

可以看出,该批次叶片在X方向的变形在2截面上波动最大,经现场分析得知在该截面存在换刀后加工叶根,故存在接刀的问题;在Y方向的变形在7截面上波动最大,是因为叶片在最靠近叶尖的截面刚性最小,故可以考虑将该截面的Y变形作为分组指标。
2.3 分组指标确定
经过叶片变形状态的分析,可以初步判断该批次叶片的弯曲变形较大,进一步通过主成分分析的方式来确定叶片最终分组所需依据的具体指标。首先对该批次的24个叶片,每个叶片都采集7个截面的X、Y方向弯曲这2个指标的数据,故有24个样本,每个样本由7×2=14个特征指标构成,最终构成一个24×14的初始样本矩阵,并对矩阵的每一列进行标准化。利用MATLAB中的pca函数对样本矩阵进行主成分分析,计算相关系数矩阵,求出特征值以及贡献率,得到特征向量矩阵,其中每一列为每一个主成分对应的特征向量。
主成分特征值以及贡献率如表1、图9所示。
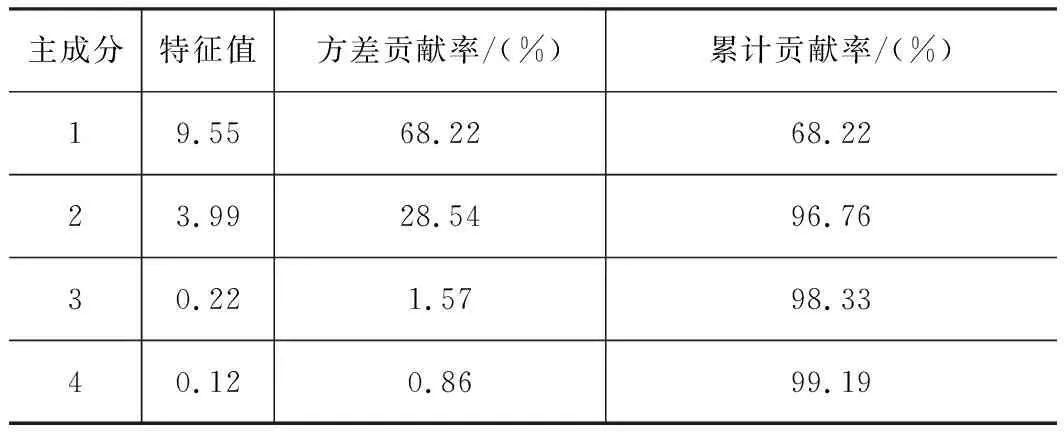
表1 特征值及贡献率表

可以看出前两个主成分已经达到数理统计中大于85%的要求,可以充分反应原指标所包含的信息,结合特征向量表可以得到用原来的14个指标描述的两个主成分的表达式,再结合每个主成分的贡献率将样本Y表述成两个主成分的表达式:
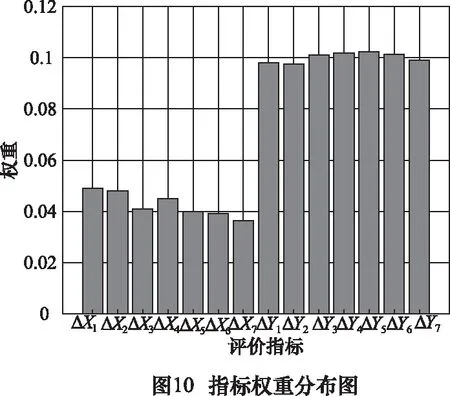
利用上文中的公式(4),将主成分单位特征向量矩阵将其乘以方差贡献率再除以累积贡献率得到各指标的权重系数,最后进行归一化处理最后得到各评价指标权重,如表2和图10所示。
可以看出Y方向的截面弯曲变形指标权重占了接近70%。说明Y向变形相较于X向变形更能反映样本的整体信息,结合图8可知Y向变形在1截面到7截面上,7截面的波动最大,可以考虑将该截面的Y变形作为分组指标。这与实际该叶片的变形情况也比较符合,该批次叶片主要是在叶盆叶背方向(接近Y方向)发生弯曲变形,且叶片在靠近叶尖即7截面处刚性最差,故在该截面也容易产生让刀变形。根据加工经验,最终将7截面的Y向弯曲变形作为分组的指标也符合生产实际需求。
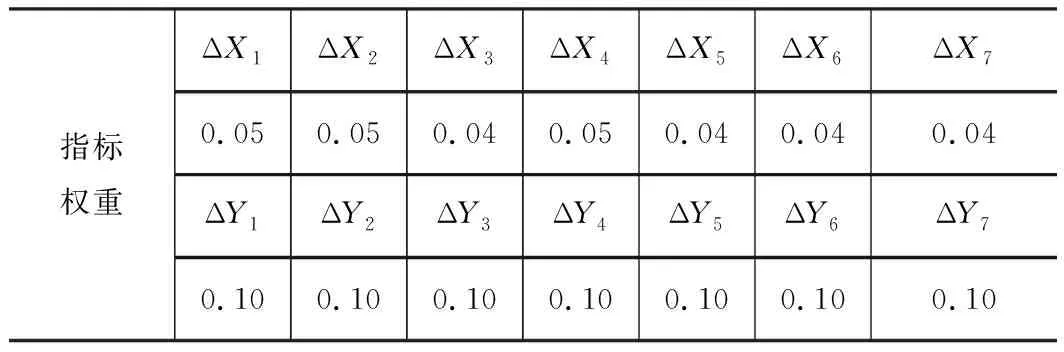
表2 指标权重表
2.4 分组过程
在确定了叶片的分组指标后,对同组叶片调整了加工坐标系后重新生成加工程序进行加工,将这一批叶片7截面Y变形作为分组指标,读出该指标的变化范围:-0.120 1~-0.047 4 mm,变化的大小为0.08 mm,根据后续阵列抛光的工艺需要,取该范围的两个三等分点进行分组判断,最终将该批次叶片分为3组,对应指标取值范围如表3所示。

表3 分组取值范围
利用编写的MATLAB程序进行数据处理后按照前述算法进行计算分析,对该批次叶片进行分组的结果如图11以及表4所示。

表4 分组结果表

2.5 实验结果与分析
对于每一组叶片,为了计算后续加工所需的坐标系调整量,依据所选分组指标7截面Y方向变形大小和对应的1截面变形再结合测量坐标系的位置,可以计算得出调整叶片余量均匀所需要在Y方向旋转的角度以及沿Y向平移距离,计算原理如图12所示。
图12中深色粗实线代表叶片产生加工弯曲变形后在YOZ平面的初始位置,浅色粗实线为叶片旋转角度θ后的位置,细虚线为正Z方向。则角度计算理论上可以分两种情况,截面1与截面7的弯曲方向一致或相反。其中Z1、Z7表示截面1与截面7在Z方向的高度,dY1与dY7表示截面1与截面7在Y方向的变形,θ1、θ2表示变形位置与坐标原点的夹角,θ表示坐标系需要旋转的角度。旋转角度后所需平移的距离即图中细虚线与粗虚线的距离。
则转角的计算公式为
(6)
根据公式(6)对3个组坐标系旋转的角度以及沿Y向平移距离计算结果如表5所示。调整加工坐标系后基于新的坐标系产生新的加工刀轨并进行加工,加工方式如图13所示。
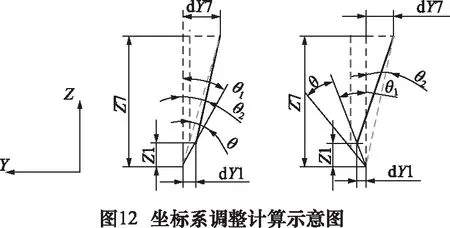
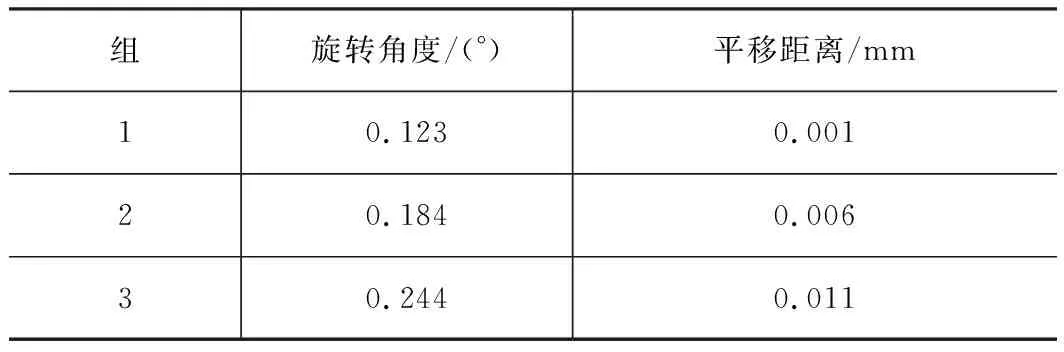
表5 坐标系变换参数表

基于分组结果以及计算出的坐标变换角度进行四阵列抛光实验,抛光所使用设备为四主轴矩形阵列抛光机床(PJZ5.04-200W),抛光工具为专用柔性抛光轮,加工过程如图14所示,同一组4阵列抛光后的4个叶片如图15所示。

获取4个阵列抛光后的叶片(编号7、11、20、22)的白光测量机抛光检测报告,报告中的数据包括叶片所测4个截面X、Y方向的中心弯曲变形偏差以及截面的相对扭角。对这4个叶片Y方向抛光后变形的数据作图进行一致性分析,如图16a所示,可以看出分组后同时阵列抛光的4件叶片Y方向变形的一致性较好,可控制在0.02 mm以内。对比随机选取未经分组加工的4件叶片(编号14、29、30、41)抛光后的结果,如图16b所示。可以看出,经过分组加工后的叶片在Y方向变形的一致性较未分组叶片有明显的提高。


3 结语
(1)提出了一种用于批次压气机叶片铣削后抛光前的基于变形特征的叶片自动化分组方法,使用主成分分析法确定了叶片的分组指标,并依据变形程度大小进行分组。
(2)对分组后的叶片进行了同步阵列抛光实验,结果表明经分组后的叶片加工一致性较高,同步阵列抛光后的四件叶片在主要弯曲方向的轮廓差异可以控制在0.02 mm以内。

