Iterative Learning Disturbance Observer Based Attitude Stabilization of Flexible Spacecraft Subject to Complex Disturbances and Measurement Noises

Tongfu He and Zhong Wu,

Abstract—To realize high-precision attitude stabilization of a flexible spacecraft in the presence of complex disturbances and measurement noises, an iterative learning disturbance observer(ILDO) is presented in this paper. Firstly, a dynamic model of disturbance is built by augmenting the integral of the lumped disturbance as a state. Based on it, ILDO is designed by introducing iterative learning structures. Then, comparative analyses of ILDO and traditional disturbance observers are carried out in frequency domain. It demonstrates that ILDO combines the advantages of high accuracy in disturbance estimation and favorable robustness to measurement noise. After that, an ILDO based composite controller is designed to stabilize the spacecraft attitude. Finally, the effectiveness of the proposed control scheme is verified by simulations.

I. INTRODUCTION

HIGH-precision attitude stabilization, including highaccuracy pointing and high-stability attitude stabilization,is essential for a spacecraft to accomplish advanced remote sensing and reconnaissance space missions, in which precision instruments are generally utilized [1], [2]. However, complex disturbances, such as environmental disturbances, flexible vibrations, parameter uncertainties, and actuator faults widely exist [3]. Meanwhile, the measurements of spacecraft attitude are inevitably contaminated by sensor and circuit noises [4],[5]. These disturbances and noises may cause performance degradation of attitude control and bring challenges to the normal operation of the precision loads. As a result,suppression of these complex disturbances and measurement noises is an important task for spacecraft control.

To achieve desirable robustness to the disturbances, many control schemes have been proposed for the flexible spacecraft control, such as proportional-derivative control [6],adaptive control [7], sliding mode control [8], and robustH∞control [9], [10]. However, the robustness of these controllers to external disturbances and flexible vibrations is generally improved at a price of sacrificing their nominal performance[2]. The consequent conservativeness of the controllers may not fully meet demand of high-precision attitude control in the presence of complex disturbances and measurement noises.An improved mixedH2/H∞controller based on poles assignment may help to reduce the problem [1]. Alternatively,a disturbance observer can be applied to give accurate estimates of the disturbances and flexible vibrations in the system. Then, by combining the observer with a robust controller, a practical composite controller for flexible spacecrafts utilizing both the measured information and the estimated information can be achieved [11]–[13]. This strategy is known as disturbance observer based control scheme (DOBC).

In DOBC, undesirable effects from disturbances,uncertainties, and flexible vibrations are estimated by an observer, and then compensated for through feedforward input signals. Thus, the robustness to disturbances of the closedloop system could be further improved and the conservativeness of the base-line controller could be reduced[14]–[16]. For these reasons, DOBC has gained increasing popularity in recent decades.

In DOBC, the estimation accuracy of disturbance observers plays an important role in achieving high-performance disturbance rejection [17]. Therefore, many efforts have been made to develop novel disturbance observers with high estimation accuracy. For instance, sliding mode techniques can be applied to the disturbance observer to reduce the effects of unmodeled disturbances on the disturbance estimation [18], [19]. However, the inherent chattering may cause complex noise problems and energy losses [20].Alternatively, an extended disturbance observer (EDO) with a high order structure can be adopted to realize high-accuracy disturbance estimation [21], [22]. However, EDO is easily affected by measurement noise when large observer gains are chosen. Measurement noises included in the disturbance estimates will be imported into the control system. It may cause heavier chattering of actuators and affect the attitude control performance. Thus, high-performance disturbance observer for spacecraft attitude control is still currently an important research topic. Except for the disturbance estimate accuracy, the robustness to measurement noise and the convenience of implementation should also be taken into consideration in the observer design.

It is noted that an iterative learning observer (ILO) is proposed by Chenet al. for faults reconstruction or disturbance estimation [23]–[25]. Traditionally, the iterative learning control (ILC) scheme is effective to improve the tracking performance of repetitive systems. For example, an adaptive ILC scheme is designed for an underactuated flexible manipulator to compensate for the repetitive trajectory invariant disturbance in [26]. In [27], anticipatory ILC scheme is utilized to reduce the effects of disturbances related to repeating ground track orbit to the satellite to improve the attitude tracking accuracy. A major difference between ILO and ILC is that the disturbance information is estimated from output of the system by ILO, and not from the control torques.Thus, in ILO based control scheme, the disturbance compensation can be realized by feedforward without affecting the feedback control of the system. The application of ILO is no longer restricted to repetitive systems or disturbances related to the repetitive trajectory [28].

Additionally, compared with conventional observers, ILO shows strong robustness to high-frequency measurement noise[29], [30]. In recent years, it has been applied in various engineering applications. The thruster faults diagnosis of satellite systems is addressed on the basis of ILO in [29]. In[30], the initial trembling problem of ILO is analyzed. In [31],sign functions are used to decrease the computing complexity of ILO. Also, a nonlinear proportional-derivative type ILO is developed in [32]. However, due to the coupling of disturbance and system state estimates in ILO, the disturbance estimation accuracy of ILO is limited compared with EDO. It is the motivation of this paper to design a novel iterative learning type disturbance observer with high estimation accuracy and adequate robustness to noise for spacecraft attitude stabilization.

To achieve high-precision attitude stabilization of a flexible spacecraft, an iterative learning disturbance observer (ILDO)is proposed in this paper. Firstly, the integral of the disturbance virtual measurement is augmented into the disturbance dynamic model as a new state. Based on it, ILDO is then constructed by utilizing iterative learning structures to update the observer. Secondly, to demonstrate the advantages of ILDO over conventional ILO and EDO, analyses in frequency domain are given when taking the measurement noises into consideration. It shows that the error dynamics between system states and disturbance estimates are decoupled in ILDO. Through ILDO, not only high-accuracy disturbance estimation but also favorable robustness to highfrequency measurement noise can be achieved. Moreover, a convenient gain tuning method for ILDO is built. Then, an ILDO based composite controller is designed to stabilize the attitude control system. Simulations are carried out for showing the improved disturbance estimation performance of ILDO over EDO and ILO. On the basis of it, the improvements of the spacecraft attitude stabilization are presented.

The remainder of this paper is organized as follows. Section II presents the model of flexible spacecraft, disturbances, and measurement noises in the system. In Section III, conventional EDO and ILO are reviewed. Then, ILDO is proposed in Section IV. Furthermore, frequency characteristics of EDO,ILO, and ILDO are compared in Section V. In Section VI, an ILDO based composite controller (ILDOBC) is designed. In Section VII, simulation results of EDO based composite controller (EDOBC), ILO based composite controller(ILOBC), and ILDOBC are presented. The conclusion is presented in Section VIII.

II. PRELIMINARIES AND MATHEMATICAL MODEL

A. Notations

B. Spacecraft Attitude Dynamics

C. Complex Disturbances

Internal and external disturbances are important hindrances to achieving high-precision attitude control of a spacecraft.The common disturbances are analyzed as follows.

As indicated by [34], the frequencies of these disturbances are typically related to the orbiting of the spacecrafts. Thus,the major components of them are slowly-varying. Also, these disturbances have upper bounds due to their existence in a physical system.

Remark1:The flexible vibrations are viewed as a part of the lumped disturbance in the system; thus their adverse effects on the spacecraft attitude can be estimated and compensated by means of the DOBC approach. Despite that,the flexible vibrations themselves are attenuated passively by the damping of the spacecraft [2]. Actually, the flexible modals will also converge with the improved control performance of the angular velocity.

Remark2:In practice, disturbances in spacecrafts cover a wide range of frequencies. However, high-frequency disturbances are generally adequately suppressed by various isolation equipment or damping equipment onboard [36]. As indicated by the in-orbit vibration test, the low-frequency attitude vibrations that mainly induced by the slowly-varying disturbances are dominant in energy [37]. Thereafter, the slowly-varying disturbances are mainly considered in the observer and controller design.

D. Measurement Noises

Measurement noises may induce chattering of actuators and even cause degeneration of attitude control performance. In practice, attitude determination systems are generally applied in the spacecraft system to process the rough attitude and angular velocity information from a series of sensors attached to the spacecraft to handle the system errors. The amounts of residual measurement noises in the obtained attitudepm(t) and angular velocity ωm(t) are depended on the quality of sensors and the performance of attitude determination algorithm [4],[38]. For simplicity,pm(t) and ωm(t) are expressed as

III. CONVENTIONAL ILO AND EDO FOR SPACECRAFT DISTURBANCE ESTIMATION

The observer structures and estimation performance of EDO and ILO are representative in the field of anti-disturbance control. Therefore, they are first reviewed in this section.

A. Design of EDO

For EDO design, the lumped disturbance is approximated by a time series expansion as follows [21], [22]:

Remark 3:EDO is a reduced-order disturbance observer in which the disturbance estimation error dynamics are decoupled from the system states [40]. EDO has been applied to various engineering due to its simple observer structure and convenient gain tuning.

Remark4:However, measurement noise is not considered in the design of EDO. When large observer gains are chosen for high-accuracy estimation, more measurement noise will be included in the disturbance estimates. Therefore, EDO is sensitive to measurement noise.

B. Design of ILO

By including iterative learning structures in the observer, a typical ILO for spacecraft dynamics is designed as follows[29]:

Remark6:In ILO, both angular velocity and disturbance are estimated. However, the attitude and angular velocity of spacecrafts are actually obtained by the attitude determination system. Thus, the estimation of angular velocity in ILO is redundant. As shown in (18), the parameters of ILO should be carefully chosen to guarantee the stability of the observer.Nevertheless, the relation between the observer gains and the estimation accuracy of ILO is not explicitly analyzed.

IV. ILDO FOR SPACECRAFT ATTITUDE STABILIZATION

To avoid the problems mentioned above, an ILDO for spacecraft attitude stabilization is designed in this section.

By taking the measurement noise into consideration, an integral state is introduced in view of (14) as follows:

Remark8:Compared with conventional ILO, the proposed ILDO has simpler structure and fewer parameters. It is explicit in concept and relatively easy to apply. The disturbance estimation error dynamics is decoupled from the system states. Also, the spacecraft angular velocity is not redundantly estimated.

V. COMPARISON OF ILDO, EDO, AND ILO

The frequency-domain characteristic reveals the feature of disturbance observer in the presence of disturbances and measurement noises that composed of various frequency components [21]. Thus, ILDO, EDO, and ILO are analyzed in frequency domain by the estimation error transfer functions as follows.

A. Estimation Error Transfer Function of ILDO

By substituting (22) and (23) into (29), the estimation error dynamics of ILDO can be given by

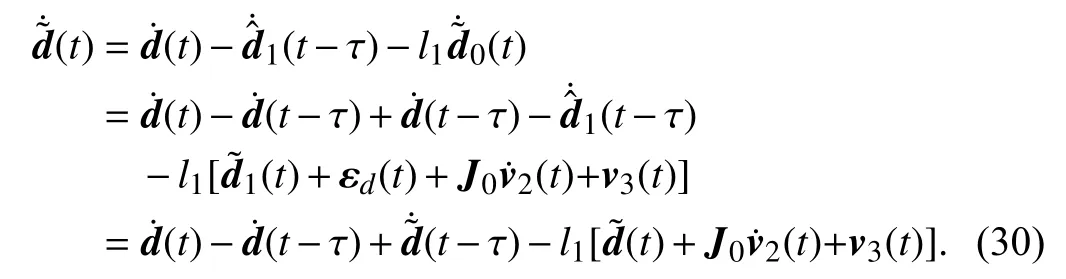
Taking Laplace transform of (30) under zero initial conditions and rearranging, we have

B. Estimation Error Transfer Function of EDO

Similarly, according to (12) and (15), the estimation error dynamics of a 2nd-order EDO (2nd-EDO) is derived as

Then, the disturbance estimation error of 2nd-EDO can be evaluated by following transfer functions:

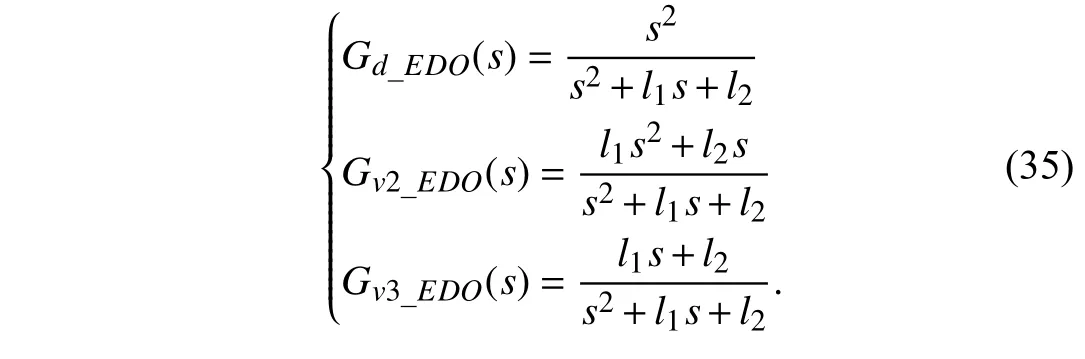
C. Estimation Error Transfer Function of ILO

To analyze conventional ILO under the same conditions,ILO (17) is redesigned as

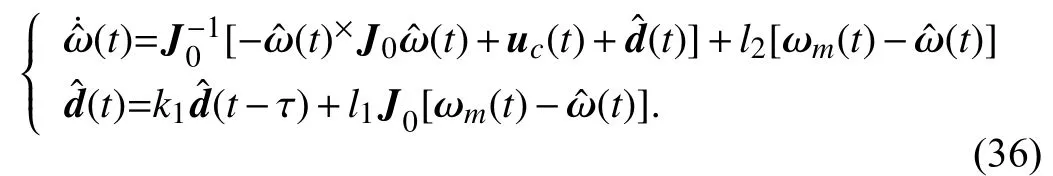
Subtracting (36) from (10) gives

Then, the disturbance estimation error of ILO can be evaluated by the following transfer functions:

D. Frequency Characteristic Comparison

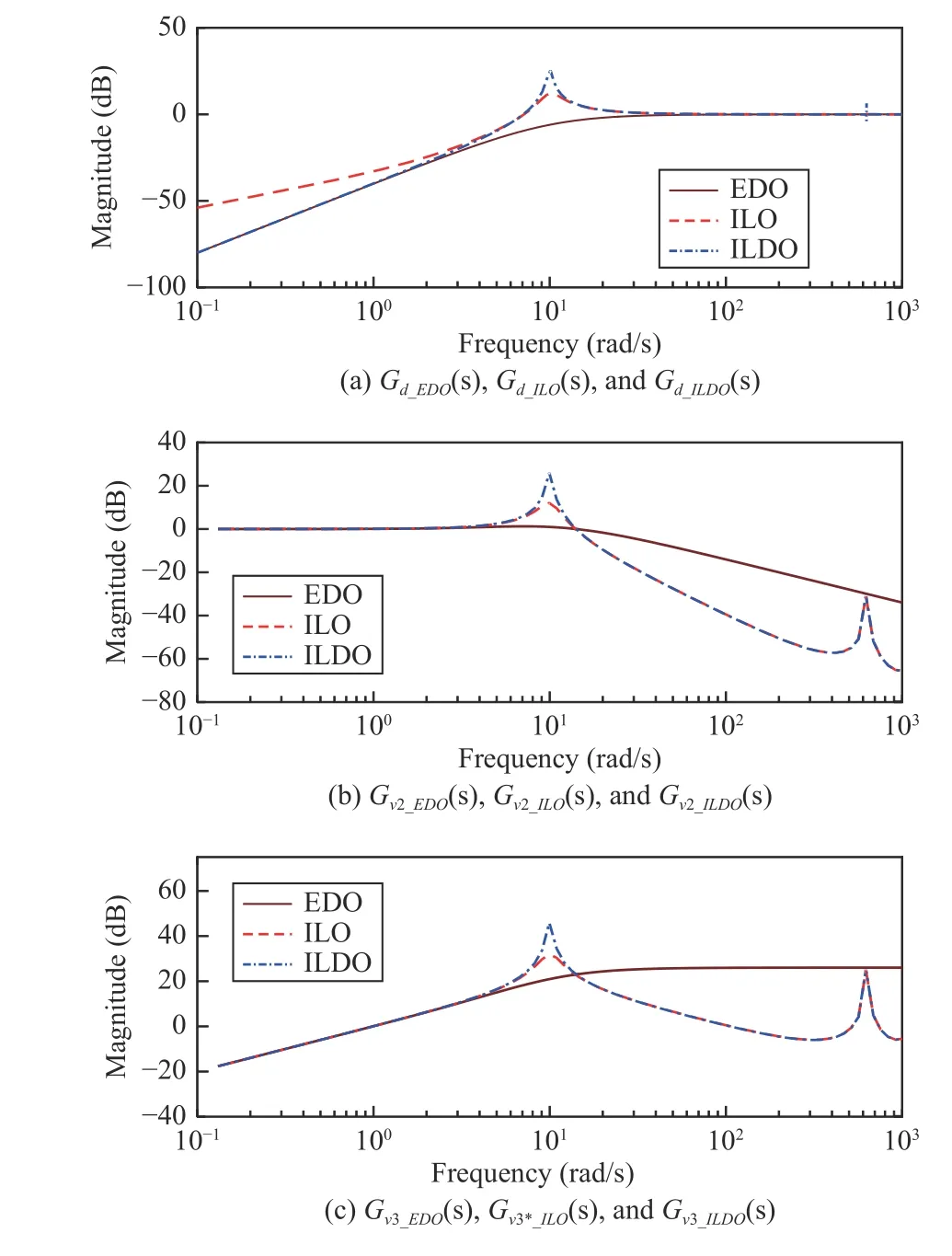
Fig. 1. Amplitude-frequency characteristics of EDO, ILO, and ILDO.

VI. ILDO BASED COMPOSITE CONTROLLER

To stabilize the spacecraft attitude system, an ILDO based composite controller (ILDOBC) is constructed following backstepping approach in this section. The schematic diagram of ILDOBC is given in Fig. 2.

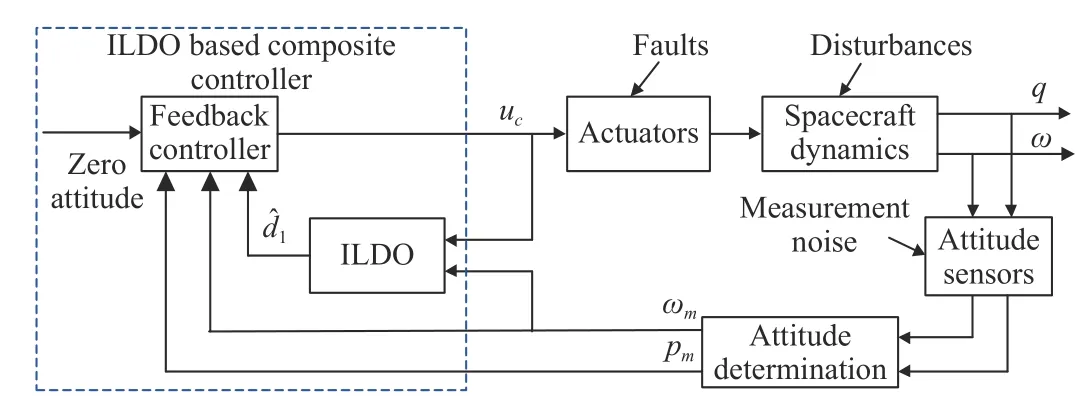
Fig. 2. Schematic diagram of ILDO based attitude control system.

Remark 10:Spacecraft attitude stabilization is affected by complex disturbances and measurement noises. In DOBC, by utilizing ILDO, most disturbances are compensated and less measurement noise from disturbance estimates is imported into the controller. Thus, the attitude stabilization performance of the spacecraft can be improved.

VII. SIMULATION RESULTS

To verify the effectiveness of the proposed ILDO based composite controller (ILDOBC), numerically simulations for a flexible spacecraft are conducted. For the comparison purpose, simulations of the feedback controller in (42) without disturbance observer (DO), EDO based composite controller(EDOBC) and ILO based composite controller (ILOBC) are also carried out.

Similar to [22], the known inertia matrix and coupling matrix of the spacecraft are assumed as

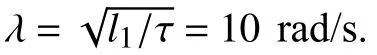
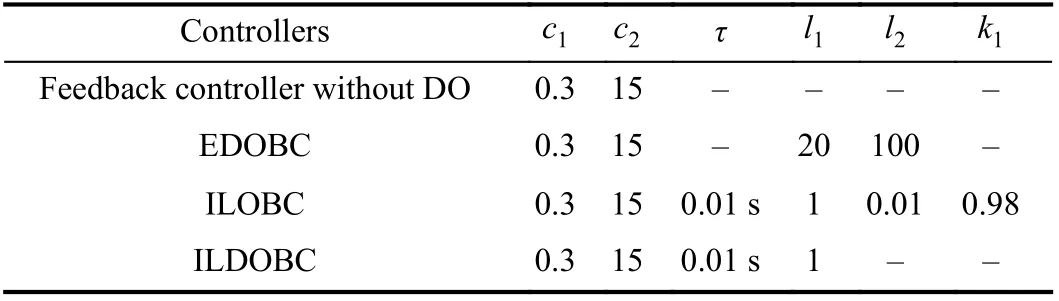
TABLE I PARAMETERS OF OBSERVERS AND CONTROLLERS

The attitude stabilization precision of the spacecraft consists of two aspects, i.e., the attitude pointing accuracy and the attitude control stability. They can be evaluated by the control accuracy of the Euler angles and angular velocities of the spacecraft respectively. In Figs. 3–8, system responses under four controllers in Table I are presented. The spacecraft attitude is described in the form of Euler angle Ω(t)=[φ,θ,ψ]Tinstead of MRP in Fig. 3. In Fig. 4, the responses of the spacecraft angular velocity are presented. In Figs. 5 and 6, the disturbance estimates and estimation errors are given. The applied control torques are presented in Fig. 7.The modal coordinates of the flexible vibrations are given in Fig

In.8 T.able II, standard deviation (STD) of Ω(t), ω(t), andare given. Also, the root mean square error (RMS) ofuv(t) is presented for denoting the chattering of control torque results from measurement noises. They are calculated using the trajectories in steady state.

As shown in Figs. 3 and 4, the attitude of the flexible spacecraft converges to a small bounded neighborhood of zero under the abovementioned controllers in Table I. However,the Euler angles and angular velocities of the spacecraft in steady-state under the feedback controller without DO are within 0.64 deg/s and 0.018 deg/s, respectively. Apparently,complex disturbances in the system significantly reduce the spacecraft attitude stabilization precision. It is difficult to meet the demand of high-precision space missions by the nominal feedback controller.

Fig. 3. Trajectories of the spacecraft Euler angles under the feedback controller without DO, EDOBC, ILOBC, and ILDOBC.

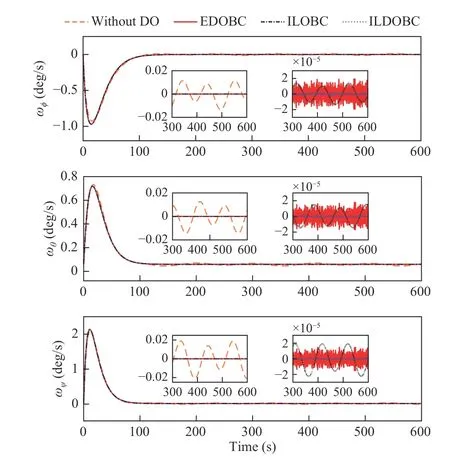
Fig. 4. Trajectories of the spacecraft angular velocity under the feedback controller without DO, EDOBC, ILOBC, and ILDOBC.

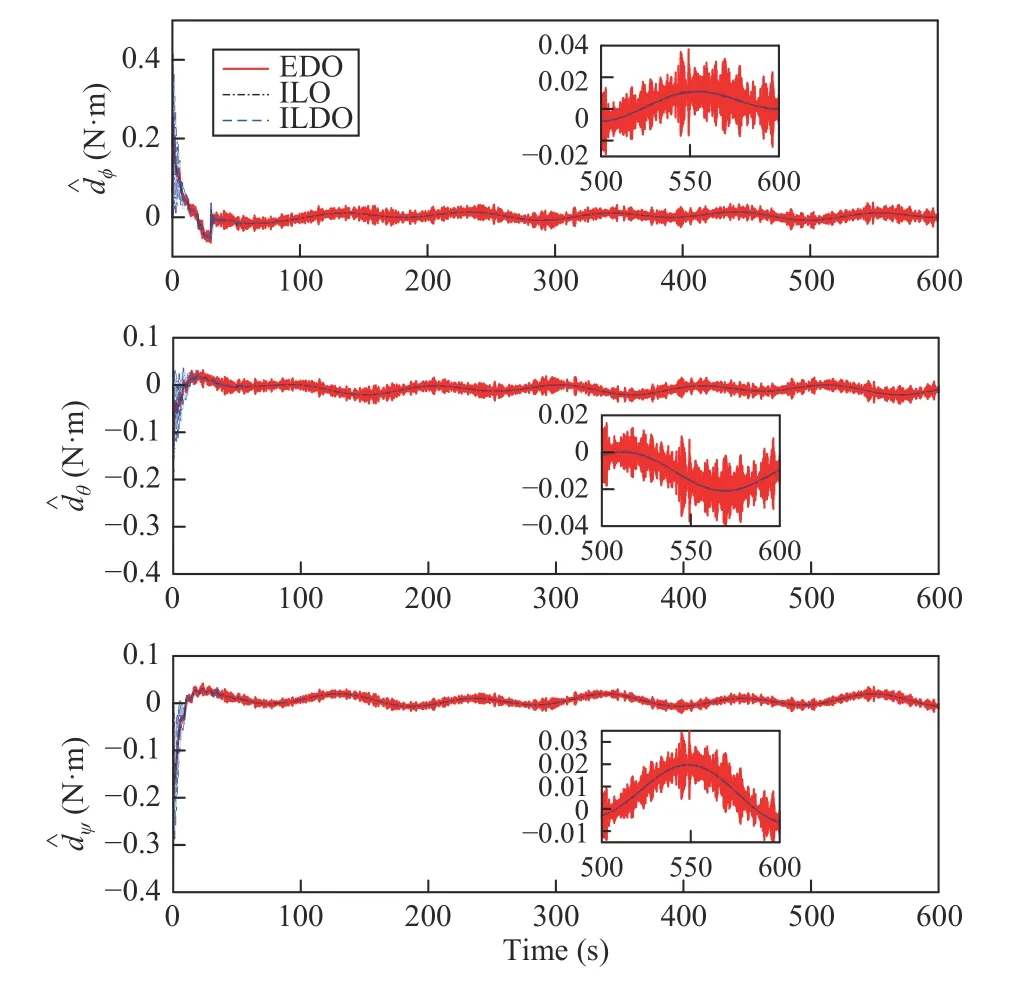
Fig. 5. Disturbance estimates of EDO, ILO, and ILDO.

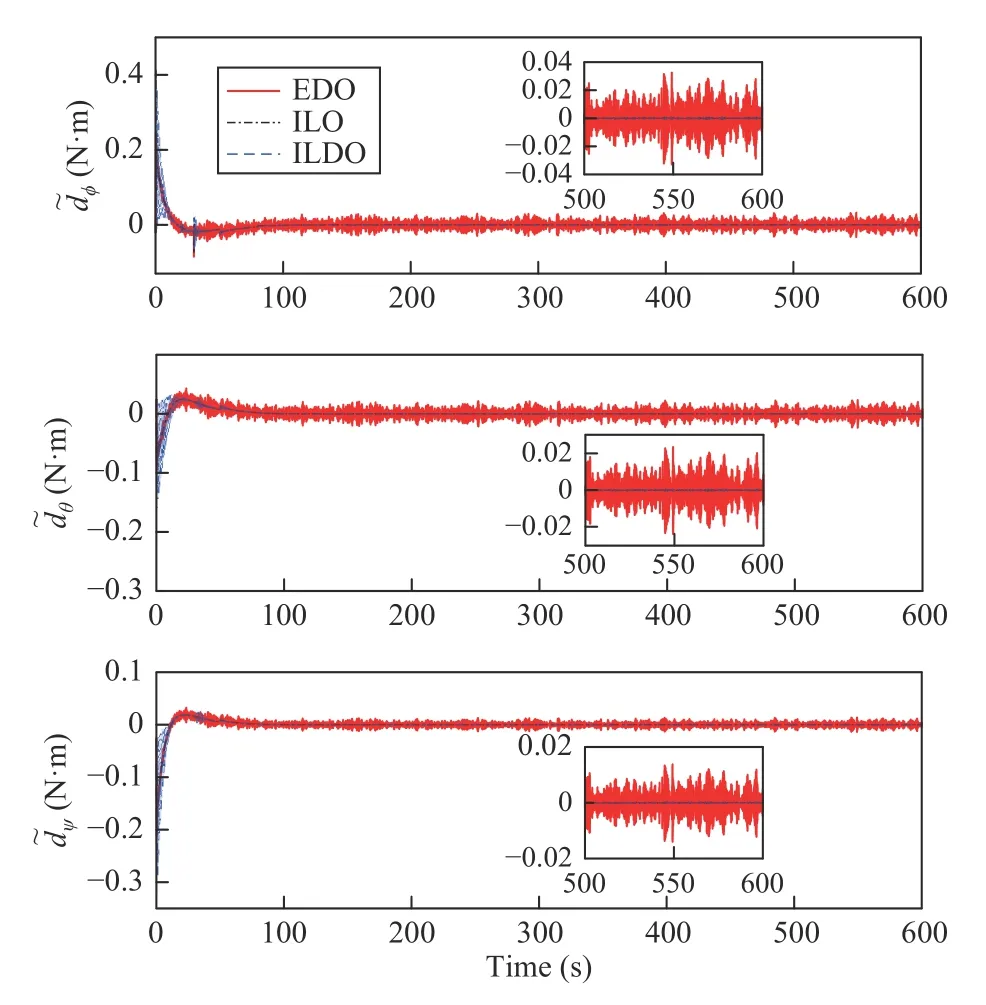
Fig. 6. Disturbance estimation errors of EDO, ILO, and ILDO.

In contrast, the attitude stabilization precision is significantly improved by the observer based controllers when their transient performance is almost the same to the feedback controller without DO. As shown in Fig. 3, the Euler angles of the spacecraft in steady-state under EDOBC, ILOBC, and ILDOBC are within 1.11×10–5deg, 4.33×10–4deg, and 1.11×10–5deg, respectively. The effects of complex disturbances are significantly reduced. By combining disturbance observers with the feedback controllers, improved robustness with respect to complex disturbances can be obtained without affecting the nominal performance of the feedback controller.

More specifically, the control accuracy of Euler angles under ILDOBC and EDOBC is improved compared with ILOBC. As shown in Table II, the STD of Euler angles under ILDOBC and EDOBC are two orders of magnitude smaller than ILOBC. Since complex disturbances and uncertainties are the main reasons that cause attitude control performance reduction, it can be concluded that that the disturbance attenuation performance of the designed ILDOBC is desirable.

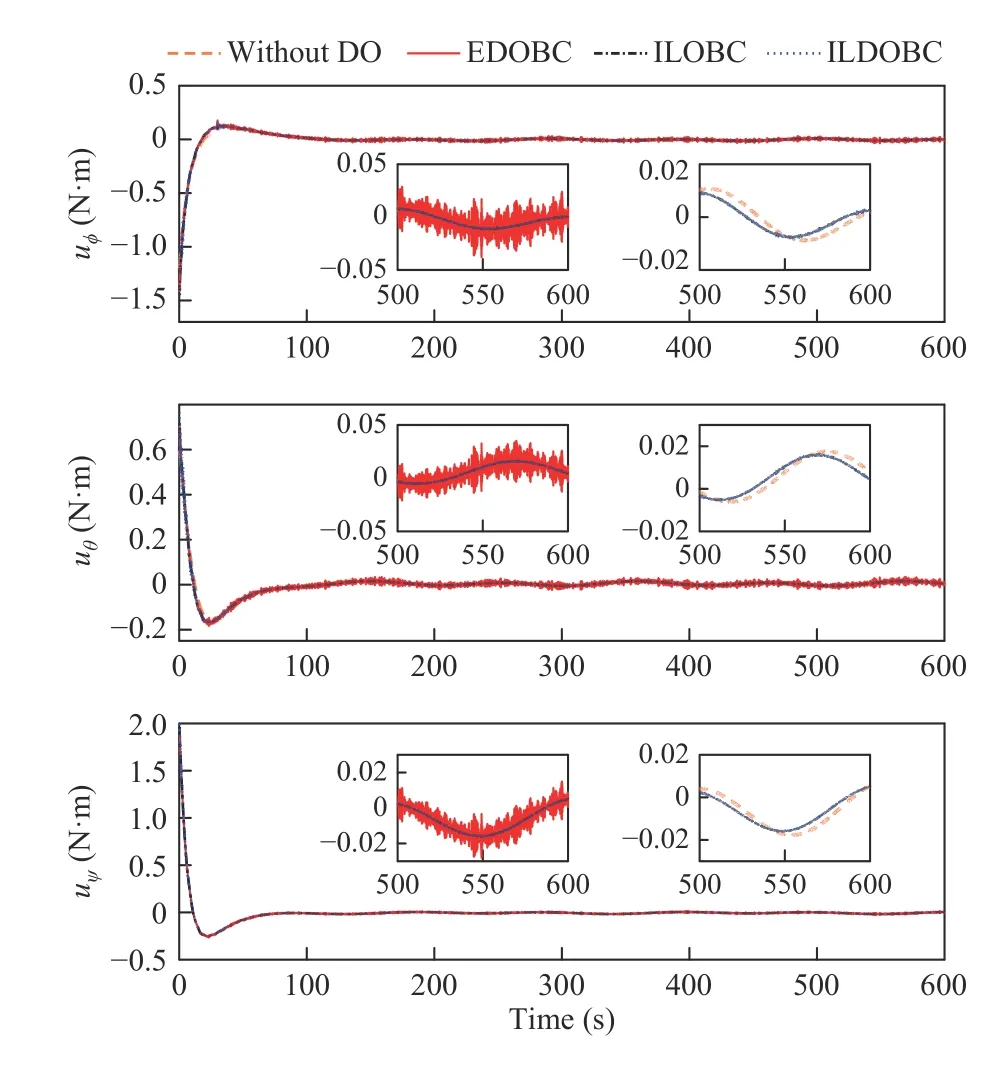
Fig. 7. Control torques of the feedback controller without DO, EDOBC,ILOBC, and ILDOBC.

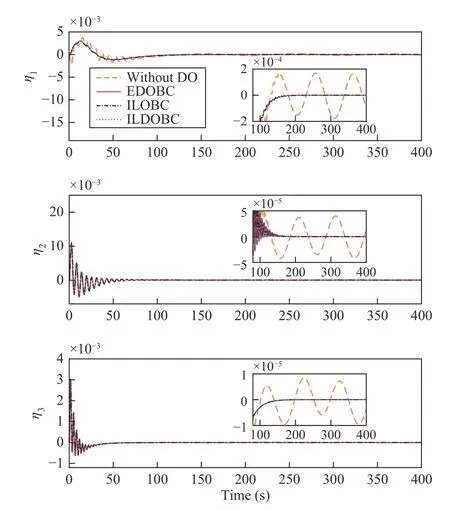
Fig. 8. Modal coordinates of the flexible vibrations.

In addition, improved control accuracy of the spacecraft angular velocities can be obtained by the designed ILDOBC compared with the other controllers. As shown in Fig. 4, the angular velocities of the spacecraft in steady-state under EDOBC, ILOBC, and ILDOBC are within 1.95×10–5deg/s,2.34×10–5deg/s, and 2.89×10–6deg/s, respectively. Specifically, the angular velocities under EDOBC are affected by heavier noises. Though the angular velocities of ILOBC contain less noise, they are still affected by theuncompensated disturbances in the system. Thus, it can be concluded that the designed ILDOBC shows not only improved disturbance attenuation performance but also adequate robustness to measurement noises.

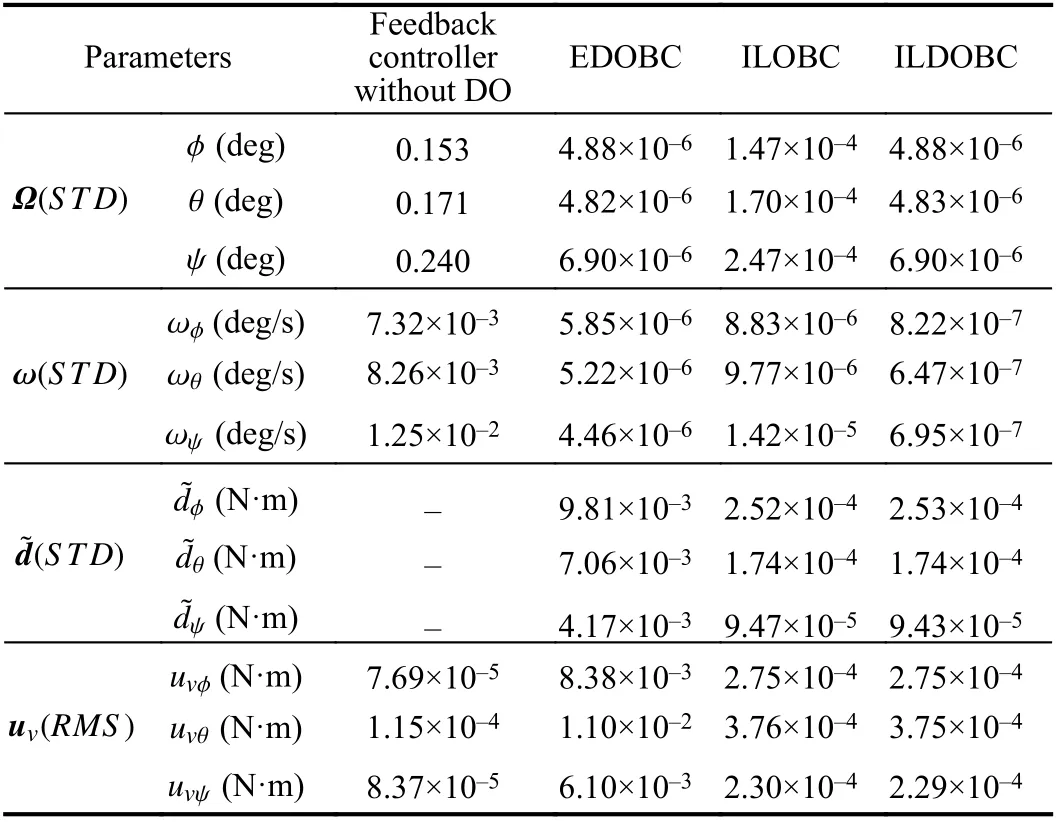
TABLE II CONTROL PERFORMANCE

It must be mentioned that the disturbance estimation errors of ILO and ILDO are relatively small values that are easily submerged by the measurement noise. Actually, the disturbance estimation accuracy of ILDO is improved compared with ILO. It can be revealed by the control accuracy of Euler angles depicted in Fig. 3. The reason is that the spacecraft Euler angles is significantly affected by the uncompensated disturbances within the control bandwidth rather than the noise with relatively high frequency components. As a result, the STD of Euler angles of ILOBC is larger than EDOBC.

The noise included in the disturbance estimates of EDO is imported into the attitude controller. It causes control performance reduction of the spacecraft angular velocity and control torques chattering. This can be observed in Figs. 4 and 7.However, due to the robustness of ILDO to measurement noise, the STD ofωunder ILDOBC is reduced about an order of magnitude compared to that under EDOBC as shown in Table II. Moreover, as shown in Fig. 7 and Table II, the control torques of ILDOBC shows more chattering than that of and EDOBC. This implies that ILDOBC can reject disturbances with smooth respond and consuming less energy.

It is noted that the effect of the flexible vibrations is compensated by the disturbance observers as a part of the lumped disturbances for improving the attitude control precision. As shown in Fig. 8, the flexible vibrations themselves are attenuated passively by the damping of the spacecraft in the observer based control scheme. However, it can be seen that there are residual flexible vibrations under the feedback controller without DO. The reason is that the angular velocity vibrations in the steady state would induce vibrations of flexible appendages persistently. In contrast, the flexible modals will converge to a smaller area ultimately under the observer based controller due to the improved control accuracy of the angular velocity.

In conclusion, it is verified that the designed ILDO combines the advantages of EDO in estimation accuracy and ILO in noise robustness. Thus, high-precision attitude stabilization of the flexible spacecraft can be achieved by the designed ILDOBC in the presence of complex disturbances a nd measurement noises.

VIII. CONCLUSIONS

In this study, a novel ILDO with high-accuracy disturbance estimation and favorable robustness to measurement noise is designed and analyzed. A convenient gain tuning method for ILDO is given. To verify its effectiveness, the ILDO based composite controller is applied to the attitude stabilization of a flexible spacecraft in the presence of environmental disturbances, spacecraft inertia uncertainties, actuator faults,and measurement noises. Numerical simulation results show that high performance disturbance estimates can be obtained and high-precision attitude stabilization of flexible spacecrafts can be achieved. In our future research, certainQfilters that are utilized in traditional ILC scheme can be combined with the designed ILDO for improving the estimation performance.Besides, the designed ILDO can be extended in the form of series or parallel configurations, and by introducing sliding mode correction terms for improving the estimation ability for fast-varying disturbances.