Distributed Resource Allocation via Accelerated Saddle Point Dynamics
Wen-Ting Lin, Yan-Wu Wang,, Chaojie Li, and Xinghuo Yu,
Abstract—In this paper, accelerated saddle point dynamics is proposed for distributed resource allocation over a multi-agent network, which enables a hyper-exponential convergence rate.Specifically, an inertial fast-slow dynamical system with vanishing damping is introduced, based on which the distributed saddle point algorithm is designed. The dual variables are updated in two time scales, i.e., the fast manifold and the slow manifold. In the fast manifold, the consensus of the Lagrangian multipliers and the tracking of the constraints are pursued by the consensus protocol. In the slow manifold, the updating of the Lagrangian multipliers is accelerated by inertial terms. Hyper-exponential stability is defined to characterize a faster convergence of our proposed algorithm in comparison with conventional primal-dual algorithms for distributed resource allocation. The simulation of the application in the energy dispatch problem verifies the result,which demonstrates the fast convergence of the proposed saddle point dynamics.
I. INTRODUCTION
A. Motivation and Related Works
RESOURCE allocation among autonomous multi-agents,which have preference over alternative resources and participate in the decision making of the resource allocation[1], has received increasing attention due to its promising applications in the smart grid [2]–[4], wireless and social networks [5]–[7], and robotics [8].
A possible approach for solving the resource allocation problem is the centralized optimization method, since the problem can be modeled into an optimization problem with globally coupled equality constraints and an uncoupled objective function. The problem exists widely, for instance, in the load sharing problem in smart grids [9], the allocation problem with 5G virtualized networks [10], the energyefficient power allocation of wireless power transfer-enabled orthogonal frequency-division multiple access (OFDMA)multicell networks [11], the peer-to-peer energy trading problem of smart grids [12], and the resource allocation of cognitive radio networks [13]. By the aid of the centralized optimization method, decision making is accomplished by solving a mathematical program. Though the centralized optimization method is feasible, it requires heavy computation for solving a large-scale resource allocation problem.Moreover, privacy issues arise with the exchange of the objective function and constraints among the agents.
As we can see, the objective function of the resource allocation problem is uncoupled. Based on this formulation,one option to solve the resource allocation problem is using the distributed optimization method over a multi-agent network. These algorithms are designed by coordinative computing among a number of agents, see [14]–[16], which overcome the disadvantages of scalability problems and privacy issues. Multi-agent based distributed optimization algorithms have been studied by many researchers, and they can be categorized as algorithms with a sub-linear convergence rate (asymptotical convergence for continuoustime systems), linear convergence rate (exponential convergence for continuous-time systems), super-linear convergence rate (super-exponential convergence for continuous-time systems) and fixed-time convergence rate.For the first category, early work in [17] is a gradient descent based method with a sub-linear convergence rate for the convex optimization problem, which cannot deal with globally coupled constraints. To address globally coupled constraints that are known by all agents, in [18], by employing the projected primal-dual sub-gradient method, an algorithm with a sub-linear convergence rate is proposed. In practice, globally coupled constraints are not always available for all agents,thus, the algorithm in [18] may lose its effectiveness unless there is a central coordinator, which means the algorithm is not fully distributed. Concerning the decoupling of the constraints, algorithms based on a continuous-time network is proposed in [19], [20], where the augmented Lagrange function is introduced for dealing with the coupled constraints. In [19], by introducing the penalty terms in the Lagrange function, the constraints are decoupled. The penalty coefficient in [19] depends on the global information of the coupled constraints, which implies the proposed algorithm is not initialization-free. In [20], by employing projected primal dual dynamics which is based on the augmented Lagrange function, an initialization-free approach is proposed. In [21],by combining the projected primal-dual dynamic with the consensus method, an initialization-free algorithm is proposed. In [19]–[21], the algorithms can only converge to the optimal solution asymptotically (sub-linear convergence rate). Recently, by using the linear Laplacian-gradient, a distributed algorithm based on a continuous-time multi-agent network is revealed in [22] for the resource allocation problem. The proposed algorithm in [22] can avoid directly dealing with coupled constraints by using an interior point method and converges asymptotically. Under the same framework, an algorithm based on a second-order network is disclosed in [23], which also shows an asymptotical convergence rate. Since the interior point method is employed,both of the algorithms in [22], [23] are not initialization-free.For the second category that can achieve exponential convergence with the globally coupled constraints being known by all agents, the algorithm of [24] over a continuoustime network is proposed, where primal-dual dynamics are employed to achieve an exponential convergence rate(corresponding to the linear convergence rate) for problems with only equality constraints. For problems with a quadratic objective, in [25], based on the primal-dual dynamics, a twotime-scale initialization-free algorithm is proposed, which can achieve an exponential convergence rate. In [26], for problems with a nonsmooth objective, differentiated projection operations and differential inclusions are introduced and a distributed continuous-time algorithm is proposed to achieve an exponential convergence rate. For the third category, in[27], an algorithm with a super convergence rate is proposed with Nesterov’s acceleration. This can achieve a super exponential convergence rate, which is faster than the conventional exponential convergence rate. However, it is limited to the unconstrained problem.
For the fourth category, note that the aforementioned distributed algorithms for constrained optimization can only reach an asymptotical or an exponential convergence rate,which cannot fulfill the efficiency demand for algorithms in engineering application. In [28], [29], by using the graph Laplacian, the fixed-time algorithm based on a nonlinear protocol for the resource allocation problem is proposed,which can converge in fixed time if the constraints are satisfied during the initialization procedure.
From the above discussion, the convergence rate of the existing distributed algorithms for solving the resource allocation problem is limited. Furthermore, fixed-time convergent algorithms require an initialization which brings additional computational cost. In this case, the requirement for the global information of the constraints in the initialization process may also lead to leakage of the privacy information with respect to the constraints.
In this paper, we will design an initialization-free distributed algorithm to solve the resource allocation problem with a faster convergence rate. By employing the inertial accelerated method, a dual accelerated algorithm is proposed for the optimization problem.
B. Contributions
The proposed algorithm can be seen with accelerated saddle point dynamics for constrained optimization. The contributions of our paper versus the existing literature are summarized as follows.
1) Accelerated saddle point dynamics are firstly proposed for resource allocation over a multi-agent network, which enables a hyper-exponential convergence rate. Hyperexponential stability is defined to characterize a faster convergence of our proposed algorithm in comparison with conventional primal-dual algorithms. With the objective function being strongly convex and its gradient being Lipschitz continuous, the proposed algorithm achieves a hyper-exponential convergence rate, which is faster than algorithms in [22]–[24].
2) The proposed algorithm is initialization-free. Although in[28], [29], the fixed-time convergent algorithm is proposed, in which convergence to the optimal solution for optimization with globally coupled constraints can be achieved in fixed time, and they require that the globally coupled constraints are fulfilled during the initialization procedure. In the proposed algorithm, we do not require that the globally coupled constraints are fulfilled during the initialization procedure,which means there is no need to reveal the information related to constraints. Therefore, privacy related to constraint information can be preserved efficiently.
3) An inertial fast-slow dynamical system with vanishing damping is introduced, based on the distributed saddle point algorithm designed. The dual variables are updated in two time scales through this formulation, which enables the acceleration of the dual dynamic. Specifically, the consensus of Lagrangian multipliers and the tracking of the constraints is designed in the fast manifold. In the slow manifold, the updating of Lagrangian multipliers is accelerated by inertial terms. This acceleration makes the proposed algorithm converge faster than saddle point dynamics in [25].
II. PRELIMINARIES
A. Notations and Definitions

Definition 1:Consider the nonautonomous system

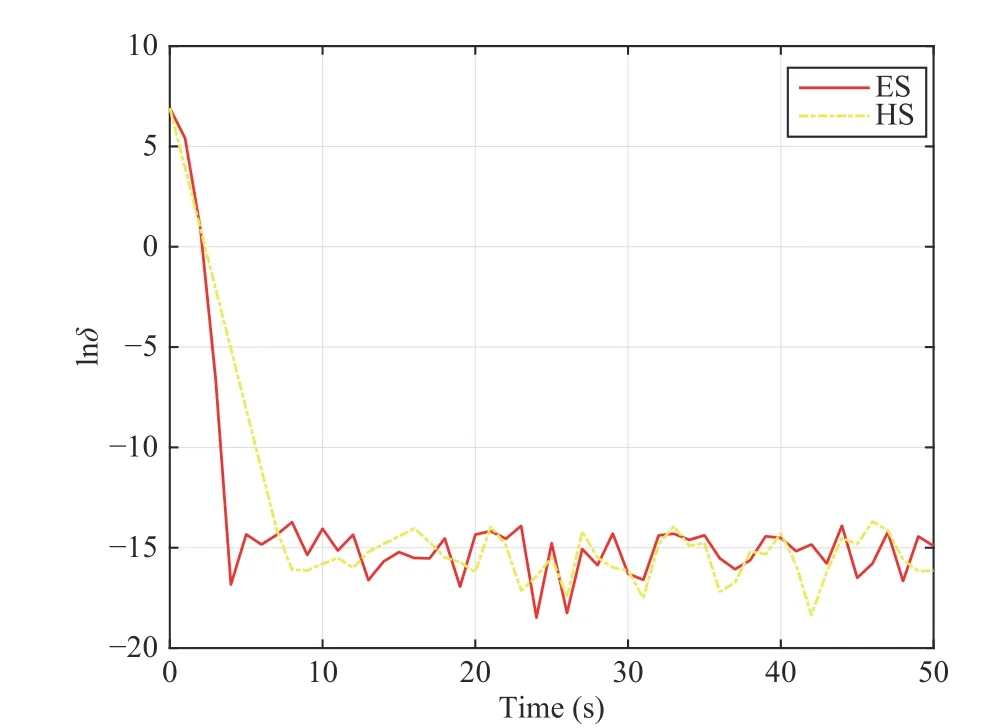
Fig. 1. The convergence rate comparison between HS and ES.


Thus, we can obtain that

Lemma 2 gives us suggestions on designing accelerated saddle point dynamics to achieve a fast convergence rate,which will be presented in the next section.
B. Problem Formulation
In this paper, the following resource allocation problem is considered
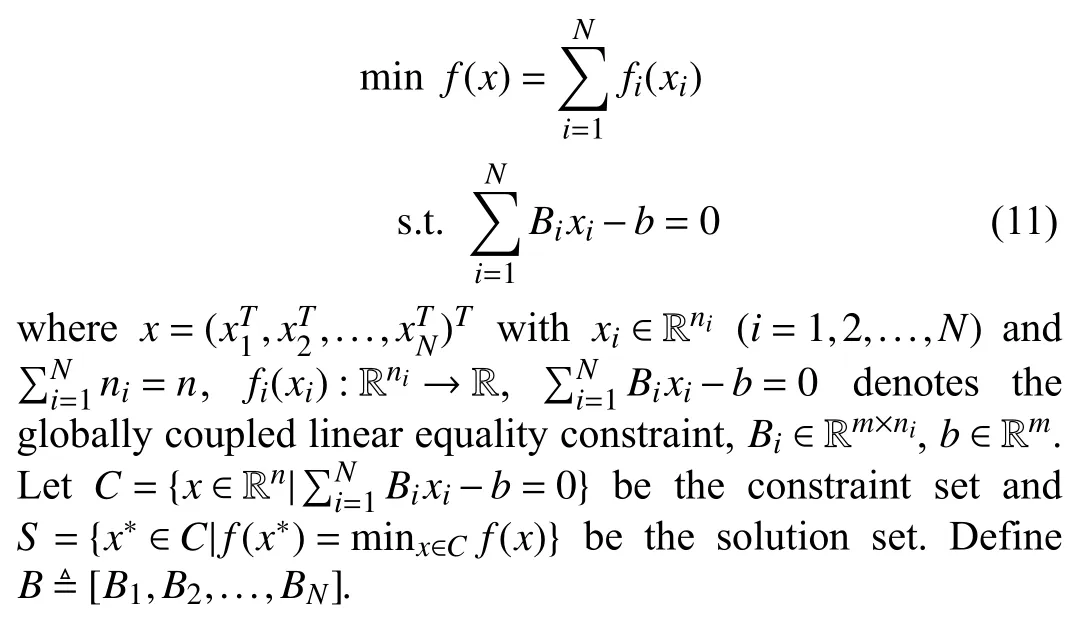
C. Assumptions

First, the Lagrangian function for (11) is constructed as follows:

Then, by characterizing the primal-dual solutions of the optimization problem as the saddle point of the augmented Lagrangian function and motivated by Lemma 2, the following algorithm is proposed for seeking the saddle point in a distributed manner


Similar to acceleration methods in [33], classical results in ODE theory do not directly imply the existence of the solutions to (14). However, through the Lyapunov analysis,we can ensure the wellposedness of (14), which will be shown in the next section.
Remark 2:Due to the introduction of saddle point dynamics, the algorithm cannot achieve fixed-time convergence, however, it is initialization-free and the coupled constraints are satisfied with the convergence of the algorithm. Compared with the centralized algorithm withO(n)computational complexity (linear complexity), the computational complexity of the proposed algorithm isO(1) (constant complexity). This means the computation complexity of the proposed algorithm will not increase with the increase of the problems’ dimension.
IV. STABILITY ANALYSIS
For the convenience of stability analysis, the proposed algorithm (14) is rewritten as follows:
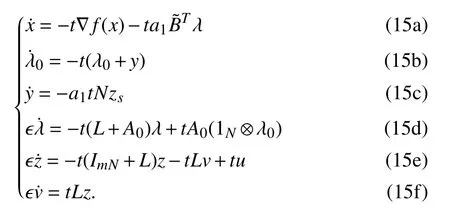

In order to show the stability of (15), we will follow the following steps. First, by employing the time-scale decomposition method (Section 11.2 in [30]), algorithm (15)is decomposed into the reduced system and the boundarylayer system. Then, the stability of these two systems are analyzed, respectively. At last, the stability analysis is combined and the stability of the whole algorithm is obtained via Lyapunov’s method.
Following the aforementioned steps, we decompose algorithm (15) first. According to the singular perturbation theorem, we can obtain the boundary-layer system as follows:

A. Stability Analysis of the Reduced System
Defineh=[xT,,yT]T. Letx∗,andy∗be the vectors satisfying the following equalities:

where





Hence, we can obtain that
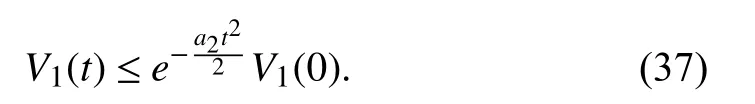
By substituting (33) into (37), we can obtain

Now, we have proven the exponential stability of the reduced model. To determine the stability of algorithm (15),we need to perform further analysis of the stability of the boundary-layer system (16).
B. The Stability Analysis of the Boundary-Layer System

where




V. APPLICATION TO THE SMART GRID
In this section, the effectiveness of algorithm (14) is illustrated by applying it to the economic dispatch problem of the smart grid, which is investigated in [29]. Here, a system with 10 generators is considered. This problem consists of finding the optimal strategy for 10 generators which minimizes the total generation cost. At the same time, the supply and demand, which can be modeled into globally coupled constraint, should be satisfied. First, based on the characteristics of power generators, similar to [22], [23] and[25] in the manuscript. The cost function of generatoriin the system can be modeled as


TABLE I THE CHARACTERISTIC PARAMETERS OF GENERATORS

A 10 agents based network is chosen to solve (67). It is undirected and circularly connected. Each agent represents one generator. The proposed algorithm (17) is used.
For comparison, the best known optimal solutions are listed in Table II, and the distributed algorithm in [22], [23] and [25]are also carried out.andC3, the relative error with algorithmC2 creeps down while it ebbs with algorithmC3, which shows a smaller slope than bothC1 andC4. Furthermore, to verify robustness of the proposed algorithm with regard to the initial condition, in Table III, under 20 sets of random initial conditions, the average convergence time ofC1,C2,C3 andC4 is compared.From both Fig. 4 and Table III, we can see that the convergence rate of the proposed algorithm (15) is faster than the algorithm with an exponential convergence rate in [25].Moreover, it is also faster that the algorithm in [22], and the algorithm in [23], which is asymptotically convergent and requires that the constraint is fulfilled during the initialization procedure. This means the inertial terms we employed in the proposed algorithm (15) perform well in the acceleration of the algorithm. Combining this with the two-time-scale property of the proposed algorithm (15), the inertial accelerated method leads to hyper-exponential stability of the proposed algorithm (15), which verifies the statement in Theorem 2.
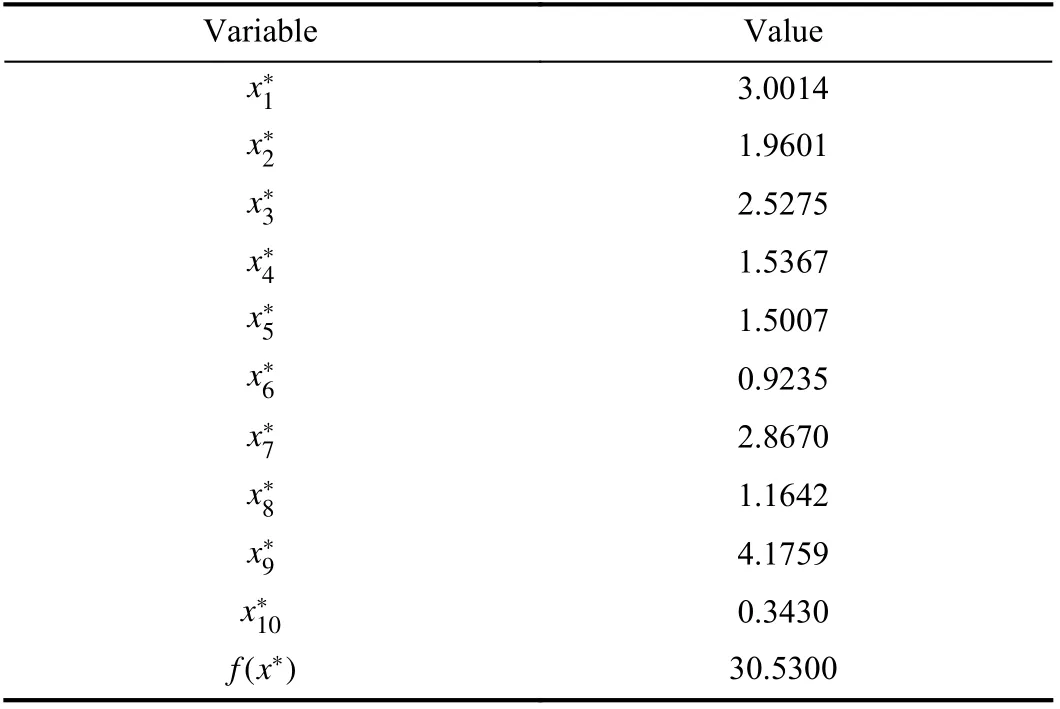
TABLE II THE BEST KNOWN OPTIMAL SOLUTIONS

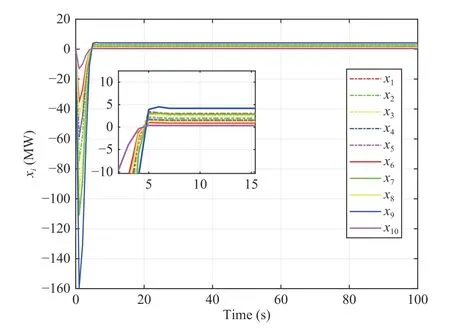
Fig. 2. The evolutions of xi (i=1,2,...,10).
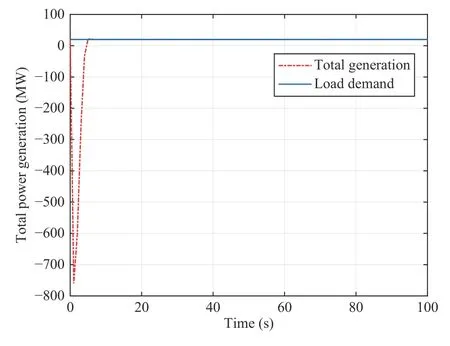
Fig. 3. The evolutions of

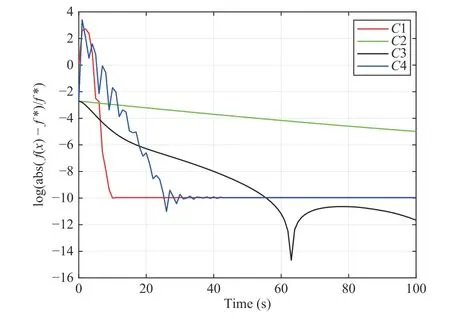
Fig. 4. The convergence rate comparison.

TABLE III CONVERGENCE TIME UNDER RANDOM INITIAL CONDITIONS
VI. CONCLUSIONS
In this paper, a distributed dual accelerated algorithm for the distributed optimization problem with coupled linear equality constraints has been proposed. By designing the algorithm in two time scales, the proposed algorithm avoids the consensus updating of the multipliers, and the tracking of constraints being executed at the same speed with saddle point seeking,which makes the inertial acceleration possible. Moreover, by introducing inertial terms in the dual dynamic, saddle point dynamics are accelerated. With the aid of saddle point dynamics, the proposed algorithm is initialization free, which means that the globally coupled constraints do not need to be fulfilled at the initialization procedure; thus, the privacy related to constraint information is well-preserved. Notably,the proposed algorithm has been proven to converge to an optimal solution faster than the ordinary saddle point dynamics, with a so-called hyper-exponential convergence rate. Simulation of the energy dispatch problem in smart grid has shown that the proposed algorithm converges faster than the exponentially convergent and asymptotically convergent algorithms.
 IEEE/CAA Journal of Automatica Sinica2021年9期
IEEE/CAA Journal of Automatica Sinica2021年9期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Fighting COVID-19 and Future Pandemics With the Internet of Things: Security and Privacy Perspectives
- Soft Robotics: Morphology and Morphology-inspired Motion Strategy
- Generating Adversarial Samples on Multivariate Time Series using Variational Autoencoders
- A Unified Optimization-Based Framework to Adjust Consensus Convergence Rate and Optimize the Network Topology in Uncertain Multi-Agent Systems
- Vision Based Hand Gesture Recognition Using 3D Shape Context
- MU-GAN: Facial Attribute Editing Based on Multi-Attention Mechanism
