Adaptive Attitude Control for Multi-MUAV Systems With Output Dead-Zone and Actuator Fault

Guowei Dong, Liang Cao, Deyin Yao, Hongyi Li,, and Renquan Lu,

Abstract—Many mechanical parts of multi-rotor unmanned aerial vehicle (MUAV) can easily produce non-smooth phenomenon and the external disturbance that affects the stability of MUAV. For multi-MUAV attitude systems that experience output dead-zone, external disturbance and actuator fault, a leader-following consensus anti-disturbance and faulttolerant control (FTC) scheme is proposed in this paper. In the design process, the effect of unknown nonlinearity in multi-MUAV systems is addressed using neural networks (NNs). In order to balance out the effects of external disturbance and actuator fault, a disturbance observer is designed to compensate for the aforementioned negative impacts. The Nussbaum function is used to address the problem of output dead-zone. The designed fault-tolerant controller guarantees that the output signals of all followers and leader are synchronized by the backstepping technique. Finally, the effectiveness of the control scheme is verified by simulation experiments.

I. INTRODUCTION

MULTI-ROTOR unmanned aerial vehicle (MUAV) has the advantages of hovering, vertical take-off and landing, and high mobility, so it is widely used in rescue missions, disaster monitoring and military surveillance [1].Attitude control is an important aspect to achieve stable flight and accurate trajectory tracking [2]. However, the MUAV is easily affected by the complex internal parts and harsh external environments in flight missions, which makes it challenging to maintain system attitude stability. In addition,the MUAV is composed of multiple components, hence, it is difficult to obtain all details of the attitude system, and there exist model uncertainties and nonlinearities. In recent years,neural networks (NNs) and fuzzy logic systems (FLSs) have been widely used in nonlinear systems due to their approximation characteristics, and various research results have been obtained [3]–[22]. Consequently, FLSs or NNs can effectively deal with uncertain nonlinear terms in MUAV system. Compared with a single MUAV system, multi-MUAV systems can complete flight missions more efficiently.Therefore, numerous distributed cooperative FLSs or NNs control schemes of multi-MUAV systems have been proposed[23]–[25]. Among them, the formation control problem of a quadrotor UAV is studied, and a nonlinear output feedback controller is developed in [23] based on NNs. For a class of multi-MUAV systems with switching and directional interaction topology, the problem of time-varying formation tracking control is investigated in [24] by NNs.

On the other hand, non-smooth phenomena (i.e., dead-zone)exist in MUAV are caused by their complex internal structure,such as engine, gear and other mechanical parts. The above situations seriously degrade stability because of system oscillations. Therefore, it is of great value to investigate the dead-zone problem of MUAV. In general, there are two kinds of dead-zone problems (i.e., input dead-zone and output deadzone). In the last several years, most of research has been related to nonlinear systems involving the input dead-zone problem [26]–[32]. In [27], the model of dead-zone is redescribed and divided into two items for compensating for the negative effects of dead-zone. For a class of switched nonlinear systems, Tonget al.[28] constructed compensation items to reduce the influence of dead-zone on control performance. In [30], the follower contains the problem of nonlinear output dead-zone, which is solved by a distributed adaptive NNs controller. It is remarkable that all aforementioned discussions about dead-zone problems are focused on the input dead-zone problem, but there are few studies on multi-agent systems (MASs) with the output deadzone problem. The output of the system is unstable due to the output dead-zone problem, which will affect the information interaction process of MASs and lead to failure of tasks. As a result for multi-MUAV systems, it is challenging to deal with the problem of output dead-zone.

Apart from internal reasons, the external complex working environment is also the reason that affects the stability of multi-MUAV systems. Multi-MUAVs usually encounter external disturbance during flight missions such as random wind, which has a great impact on the attitude control of multi-MUAV systems [2]. For the sake of solving the external disturbances better, the disturbance observer design method is proposed to estimate and compensate them in the controller[33]–[37]. A synthetic disturbance including the NNs approximation errors, unknown asymmetric input saturation,and external disturbance is considered in [34], which is estimated by the disturbance observer. At the same time, the MUAV internal structure is precise and the external working environment is complex, therefore the occurrence of fault is inevitable. Hence, it is necessary to exploit the fault problem of MUAV system. So far, to the best of our knowledge, there are few reports on adaptive attitude control for multi-MUAVs by considering the influences of output dead-zone and actuator fault.

Inspired by the aforementioned discussions, in order to ensure the stability and tracking accuracy of multi-MUAV attitude systems, it is important to consider the above unfavorable factors when designing the flight controller. For this purpose, this paper studies the anti-disturbance and faulttolerant control (FTC) method for multi-MUAV systems with the output dead-zone problem. The main contributions can be summarized as follows.

In [27]–[30], only the input dead-zone is considered rather than the output dead-zone. Moreover, in [38]–[40], in spite of considering the output dead-zone effect, the studied plants are general nonlinear systems, which can not be directly applied to multi-MUAV systems due to its complexity caused by the information interactions. In comparison with [27]–[30],[38]–[40]， this paper exploits attitude control for multi-MUAV systems with an output dead-zone by means of a Nussbaum function. The influence of the output dead-zone problem on attitude control can then be effectively reduced by the designed controller.

The influence of external disturbance on the system is suppressed in [34], [35], but the problem of fault is not considered. In addition, in [36], although the problems of fault and unknown external disturbance are considered at the same time, it is aimed at the common nonlinear system rather than a multi-MUAV systems. Fault and the unknown external disturbance are inevitable for multi-MUAV systems in flight missions. Therefore, it is necessary to investigate the problem with respect to the fault and unknown external disturbance.Unlike the existing results in [34]–[36], a disturbance observer is proposed in this paper to estimate the disturbance and fault,and incorporate the disturbance estimation into the controller to actively compensate for the disturbance.

II. PROBLEM STATEMENT AND PRELIMINARIES

A. Graph Theory

B. Model of Six-Rotor UAV

Fig. 1. Structure of the six-rotor aircraft.

In this paper, on the basis of the MUAV model in [2], the attitude system can be rewritten as

Taking the model and disturbance uncertainties into account, the attitude model with three channels (i.e., roll channel, pitch channel and yaw channel) is expressed as

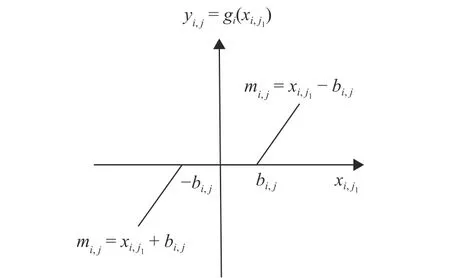
Fig. 2. Symmetric output dead-zone model.

The considered system contains actuator bias fault, which is expressed as follows:

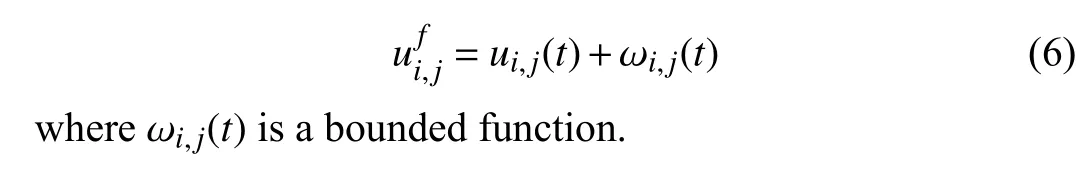
C. Nussbaum Function Properties

In order to solve the unknown dead-zone output problem, a Nussbaum-type functionN(ξi,j) is introduced, which satisfies the following equations:

D. RBF NNs

III. ADAPTIVE NNS ATTITUDE CONTROLLER DESIGN

Based on the framework of backstepping design method, the distributed adaptive anti-disturbance FTC strategy and parameter adaptive laws are proposed in this section.

In the light of (14) and (15), it follows that

Substituting (20) and (21) into (19), a straightforward calculation yields

It follows from RBF NNs that (28) holds.

The Lyapunov function is selected as

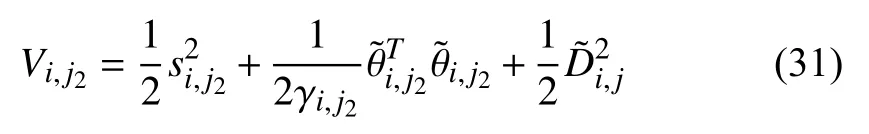
Applying Young’s inequality, Assumptions 1 and 2 achieves

IV. STABILITY ANALYSIS

The above distributed anti-disturbance FTC strategy and stability analysis are summarized in Theorem 1.

Theorem 1:Under Assumptions 1, 2 and Lemma 1, we consider the attitude systems (2) with actuator fault and output dead-zone. If the virtual controller (23), the disturbance observer (29), the anti-disturbance fault-tolerant controller(38), the adaptive laws (24) and (39) are designed, then, all signals involved in the closed-loop system can be ensured to be bounded, and the tracking errors converge to a small neighborhood of zero.

Proof:The time derivative of the Lyapunov candidate function is derived as

By using Young’s inequality, one has

V. SIMULATION RESULTS

The following simulation results are presented to demonstrate the effectiveness of the proposed anti-disturbance fault-tolerant controller under the communication graph in Fig. 3, and the occurrence time of faults and disturbances is explained in Fig. 4. Based on the communication graph, the Laplacian matrix ℸ and adjacency matrix Λ are obtained as follows:

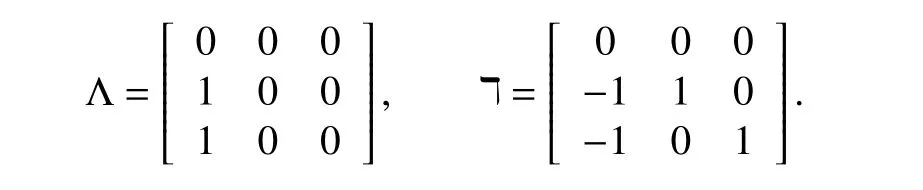
Fig. 3. Communication graph.

Fig. 4. The occurrence time of external disturbances and actuator fault of MUAVs #1–3.

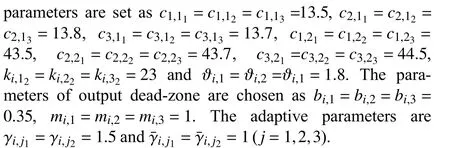
In this paper, the actuator fault occurs in MUAV#1, the fault function is ω1,j(t)=0.1+sin(2πt), and other MUAVs are normal. In order to simulate the real flight environment, the external disturbances are wind disturbances, whose direction and level are different. We add different disturbance signals in each MUAV to carry out anti-disturbance test. The selected disturbance functions are as follows:Fig. 5 exhibits the tracking results of three attitude channels.Apparently, our proposed anti-disturbance FTC scheme can achieve the flight target under the unknown symmetric output dead-zone as well as external disturbances and actuator bias fault, the attitude systems can track the desired trajectories well by offsetting various adverse factors. The external disturbance and actuator fault in the closed-loop system are estimated by the disturbance observer, and are further compensated by the controller. The trajectories of tracking errors are shown in Fig. 6. The trajectories of control inputsuiare illustrated in Fig. 7. Fig. 8 shows the degree of the disturbance observer (29) to estimate external disturbances and actuator fault. It should be noted that when the actuator in MUAV#1 becomes faulty, even if each MUAV has a large external disturbance and the occurrence time and direction are uncertain, the designed disturbance observer can compensate for these uncertainties well in multi-MUAV systems.

Fig. 5. The trajectories of yφ,i, yθ,i, yφ,i and yj,r.

VI. CONCLUSIONS

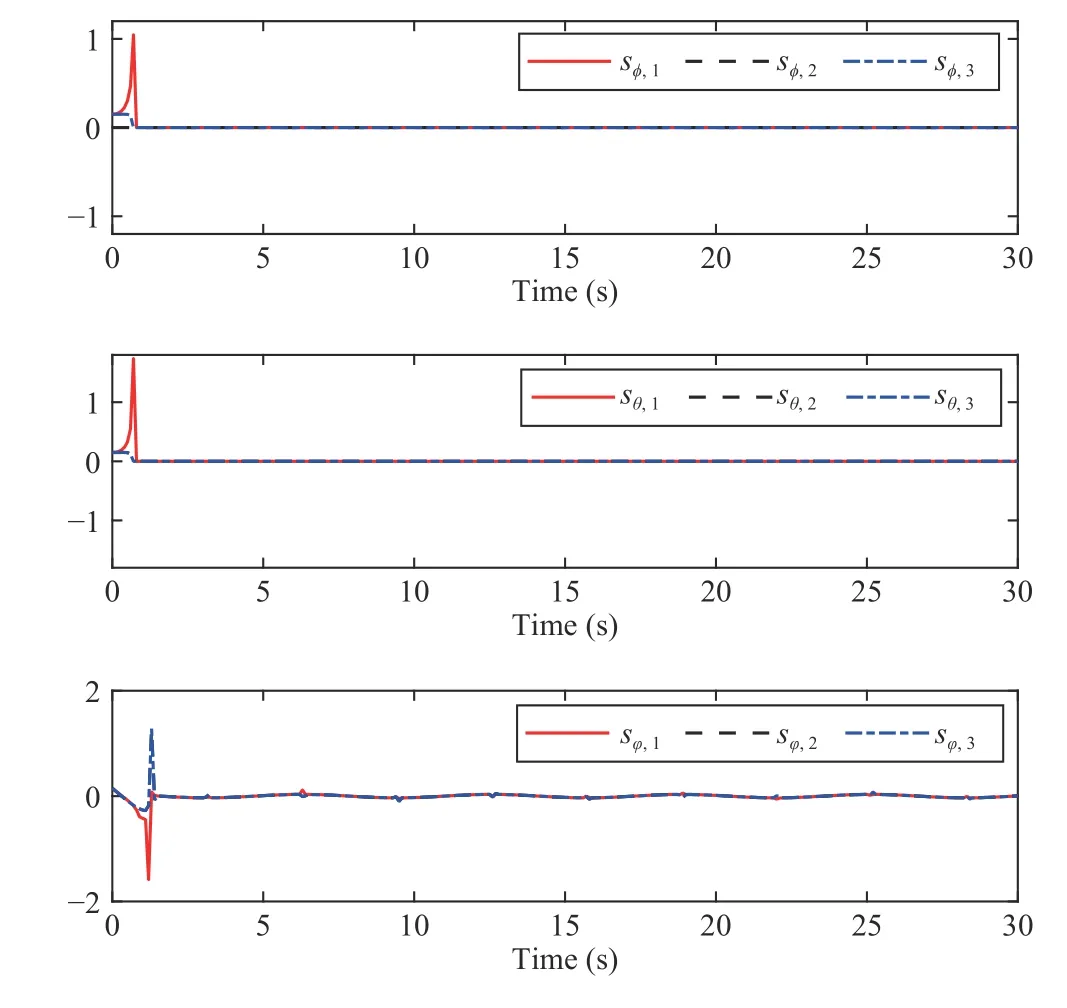
Fig. 6. The trajectories of sφ,i, sθ,i and sφ,i.

Fig. 7. The trajectories of uφ,i, uθ,i and uφ,i.

For a class of multi-MUAV systems under external disturbance, output dead-zone and actuator fault, the tracking tasks of attitude control have been considered. A distributed anti-disturbance FTC method in conjunction with Nussbaum function, adaptive NNs, and disturbance observer has been proposed for the attitude system. By introducing a disturbance observer to compensate for external disturbance, the influences of external disturbance and actuator fault on multi-MUAV systems have been suppressed. The property of Nussbaum function is introduced to handle the output deadzone problem. Furthermore, by designing appropriate parameters, all signals are bounded and the stability of the closed-loop system is ensured. These results further demonstrate the effectiveness of the proposed control strategy.For practical applications [46], numerous challenging problems should be considered, including that of communication constraints [47], finite-time connective control[48] and learning control [49]. Therefore, the results of this paper will be extended to communication constraints, finitetime control and learning control for multi-MUAV systems or unmanned ground vehicles systems [50].

Fig. 8. The trajectories of and Di.