桥梁线形控制中的灰色预测模型数据优化

秦双双，田尔布，张依然，王常峰

（1.三明学院 建筑工程学院，福建 三明，365004；2.北京国道通交通公路设计研究院股份有限公司，北京，100000 3.烟台大学 土木工程学院，山东 烟台，263005）

目前国内桥梁建设正朝着大跨度新型式的桥梁方向不断发展，为了确保满足设计线形以及梁体施工的安全性，必须进行施工控制[1-2]。施工控制理论主要有BP神经网络、Kalman滤波法、灰色控制理论、最小二乘法等[3-4]。桥梁线形预测常用的方法为灰色理论GM(1,1)预测模型，灰色控制理论[5]自邓聚龙教授于1982年提出后便应用到各行业。它的特点是它所需数据量小，实时性好,通过现有数据来进行数据加工与处理,应用范围广泛。近年来，国内外诸多学者在预测模型上做了大量的研究。姚荣[6]在（61+110+61 m）连续刚构桥的施工监控中对比分析了采用4个、6个样本数据的GM(1,1)模型以及采用4个样本数据的GM(2,1)模型进行立模标高值的预测结果，结果表明对于GM(1,1)模型，采用4或6个样本数据对精度影响小，而在样本数据相同情况下采用二阶GM(2,1)模型精度更高，并且4个样本数据的二阶GM(2,1)模型与实际吻合程度最高。张熙胤等[7]提出了一种多变量GM(1,n)关联预测模型，应用在预应力混凝土连续梁的高程预测中，对不同施工工况中出现的误差进行单独分析和及时修正，在桥梁施工控制中取得了很好的效果。彭官友[8]提出了基于累积法的灰色预测模型，在湖南龙永高速红岩溪大桥的标高预测中对比分析了传统GM(1,1)模型和改进GM(1,1)模型的预测精度，结果表明，后者预测精度更高，并且相比传统 GM(1,1)灰色预测模型，降低了异常值的出现。段宝福[9]建立了新陈代谢GM(1,1)模型和SCGM(1,1)滚动模型，应用在宁杭客专南河大桥施工应力控制中，结果表明两种模型均能满足精度要求。于玲[10]将灰色理论应用在控制斜拉桥的静载试验中，建立了基于函数1/xn变换的灰色模型，n取1/8、1/4、1/2、1、2、4等不同的数值，对斜拉桥的钢箱梁最大挠度工况的挠度进行预测，结果表明，n值取得越小，预测精确度越高，并且，这种优化的GM(1,1)模型对于斜拉桥因加载过大使桥梁受损的方面上起着预防作用。程霄翔[11]为了探索悬臂施工中连续梁桥的应力变化规律，建立多个灰色GM(1,1)模型，结果表明，滚动GM(1,1)灰色模型具有较强的自适应性，可改善预测精度，并应用在黄沙港大桥的应力控制中。

由于现场实测数据往往波动性大，尤其大跨度连续刚构桥，施工难度大，导致常规GM(1,1)模型预测效果不稳定，存在一些预测偏差过大的情况[12-14]。本文对 GM(1,1)预测模型存在的缺陷提出改进办法，对原始序列进行曲线拟合处理，建立四种数据模型对某预应力连续刚构桥线形进行预测，找到精度更高的预测方法。

1 GM（1,1）灰色预测模型

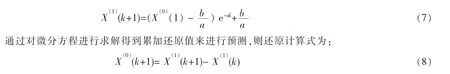
2 预测模型工程实践应用对比

2.1 工程概况

现有一座某预应力连续刚构桥，全桥长310 m，跨径布置为 80＋150＋80 m，并采用北京迈达斯公司的2017版有限元软件midas civil建立桥梁有限元模型，如图1所示。主梁截面为单箱单室斜腹板变高度。梁底下缘按二次抛物线变化，全桥共64个施工号块，其中悬臂节段每个墩两侧各14个，边跨现浇段长5.5 m，跨中和边跨合拢段均为2 m。箱梁采用挂篮对称悬臂施工。

图1 （80+150+80）m连续刚构桥有限元模型

2.2 GM（1,1）模型预测

大量研究表明，灰色理论预测模型对于离散型较大的数据序列，预测精度往往不是很高[15-16]。为了提高预测的精度，本文对124号墩小里程侧各节段号块的实测位移值进行预处理，利用Excel表进行拟合，来减小数据的波动性。图2为124号墩小里程侧5#～14#块混凝土浇筑实测位移值数据的拟合曲线图。从图中可以看出5#～9#块阶段的位移实测值与理论值的吻合程度较好，而10#～14#块阶段的位移实测值波动性较大，但总体来说实测数据值上下波动的特点与理论值的变化曲线较为一致，呈二次多项式曲线模式，故利用excel表的拟合曲线功能求出该条曲线的公式为

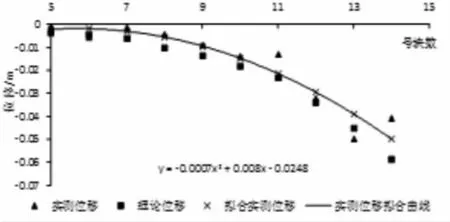
图2 5～14#块实测位移数据拟合图

从而可以计算得到拟合后的5#～14#块的位移实测值。采用悬臂现浇施工的 124V墩的小里程侧连续节段第5#～14#现场测得的混凝土浇筑位移实测值、有限元软件建模计算的各节段的理论值以及利用拟合曲线(图1)求得的实测值见表1所示。

表1 5～14#混凝土浇筑位移数据汇总表

为了找到灰色理论预测精度方法，这里采用四种方法对原始数据进行处理来预测该连续刚构桥124#墩小里程侧14#节段的混凝土浇筑位移值。于是基于前面表1中的5#～14#节段数据，使用分别采用拟合前后实测值与理论值的差值和比值作为原始数据的 GM（1,1）模型来预测要求的实测值。

预测值精度采用相对误差：

（1）采用未进行拟合的实测值与理论值的差值进行预测

第一步：由于10#～13#块未拟合的实测值与理论值的差值均为负值，GM（1,1）模型要求原始序列均为非负数，故需要进行非负化处理。将差值均加上负数中绝对值的最大者即0.004 7后，生成灰色原始序列X(0)=[0.00883,0.01484,0.00644,0]

第二步：X(0)做1-AGO，得：X(1)=[0.02367,0.03851,0.04495,0.04495]

第三步：生成紧邻均值序列即Z(1)=[0.03109,0.04173,0.04495]

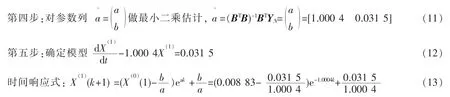
第六步：计算 X（1）序列，经过1-AGO还原得预测数据序列为[0.008 8,0.014 3,0.005 3,0.001 9]；14#块还原值为0.000 71，理论位移值为-0.058 74 m，实测位移值为-0.040 82 m。为消除非负化处理的影响，需减去非负常数0.004 7，故124#墩小里程侧14#块混凝土浇筑时的预测位移值为-0.058 7 4+0.000 71-0.004 7=-0.062 73 m；易得浇筑14#节段预测值与实测值的绝对误差为：-0.040 82-（-0.06273）=0.021 91 m。浇筑14#节段预测值与实测值的相对误差为54%。

（2）采用拟合的实测值与理论值的差值进行预测

利用10#～13#块拟合后的实测值与理论值的差值生成灰色原始序列为X（0）=[0.003 45,0.001 62,0.004 38,0.006]，因均为正值，不需要进行非负化处理。预测方法和步骤与前面相同，限于篇幅这里不再赘述，并利用Math Works公司的2020版matlab软件进行编程运算，提高效率。

同理，采用拟合后的实测值与理论值的差值作为原始序列经计算求得的14#块还原值为0.010 2，理论位移值为-0.058 74 m，实测位移值为-0.040 82 m。故124#墩小里程侧14#块混凝土浇筑时的预测位移值为-0.058 74+0.010 2=-0.048 54 m；易得浇筑14#节段预测值与实测值的绝对误差为：-0.040 82-（-0.048 54）=0.007 72m。浇筑14#节段预测值与实测值的相对误差为15.4%。

（3）采用未拟合的实测值与理论值的比值进行预测

利用10#～13#块未拟合后的实测值与理论值的比值生成灰色原始序列为X（0）=[0.773 70,0.561 42,0.948 79,1.104 21]，因均为正值，不需要进行非负化处理。

同理，采用未拟合的实测值与理论值的比值作为原始序列经计算求得的14#块还原值为0.859 0，理论位移值为-0.058 74 m，实测位移值为-0.040 82 m。故124#墩小里程侧14#块混凝土浇筑时的预测位移值为-0.058 74×0.859 00=-0.050 46 m；易得浇筑14#节段预测值与实测值的绝对误差为：-0.040 82-（-0.050 46）=0.009 64 m。浇筑14#节段预测值与实测值的相对误差为23.6%。

（4）采用拟合的实测值与理论值的比值进行预测

利用 10#～13#块拟合后的实测值与理论值的比值生成灰色原始序列为 X（0）=[0.810 96,0.92993,0.871 10,0.866 96]，因均为正值，不需要进行非负化处理。

同理，采用拟合后的实测值与理论值的比值作为原始序列经计算求得的14#块还原值为0.827 5，理论位移值为-0.058 74 m，实测位移值为-0.040 82 m。故124#墩小里程侧14#块混凝土浇筑时的预测位移值为-0.058 74×0.827 5=-0.048 61 m；易得浇筑14#节段预测值与实测值的绝对误差为：-0.040 82-（-0.048 61）=0.007 79 m。浇筑14#节段预测值与实测值的相对误差为15.6%。

2.3 模型预测结果比较

从上节4种模型的结果可以看出，采用实测值与理论值的差值建立GM(1,1)模型预测14#位移值，拟合前绝对误差为0.021 91 m，拟合后绝对误差仅为0.007 72 m，相对误差由54%降到了15.4%；同样，采用实测值与理论值的比值建立GM(1,1)模型预测14#位移值，拟合前绝对误差为0.009 64 m，拟合后绝对误差仅为0.007 79 m，相对误差由23.6%降到了15.6%。

若只对14#块的预测结果进行分析，预测结果可能存在偶然性。为了增加结果的可靠性，对124#墩小里程侧9#～13#块的位移值也建立以上四种数据的模型进行预测。为了直观对比拟合前后采用实测值与理论值的差值作为数据序列建立 GM(1,1)模型预测和采用实测值与理论值的比值作为数据序列建立 GM(1,1)模型预测的精度，将四种数据模型预测得到9#～14#块预测值与实测值的差值以及误差百分比绘制成4种折线，如图3所示。从图中可以看出，9#～13#块的四种数据模型预测精度表现出与14#块预测精度相同的规律性，验证了前面结论的可靠性。

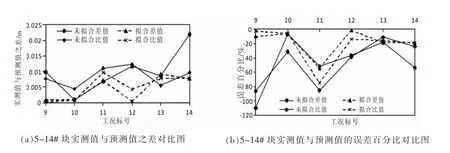
图3 5～14#块实测值与预测值的误差对比图

3 结论

本文在研究了4种数据的GM(1,1)模型之后，获得3点主要结论。

（1）利用Excel表的拟合曲线功能对实测位移数据进行了拟合处理后，可以有效解决原始数据离散性和波动性较大的问题。无论是采用实测值与理论值的差值还是实测值与理论值的比值建立GM(1,1)模型，通过excel表对实测数据拟合处理之后预测精度会更高。

（2）GM(1,1)模型的预测精度对现场实测数据的测量精确度具有较强的依赖性。若实测数据离散性较大，模型预测精度会大大降低，所以在实际施工监控过程中要注重测量方法以及测量仪器的精准操作，确保实测数据的准确性。

（3）采用经过拟合处理后的实测数据进行 GM(1,1)模型预测，预测值与实测值的差值均在 1.0cm以内，精度更高，适用性更强。