基于莱维飞行和自适应权重的水波优化算法

周建萍，贾鹤鸣，王 爽

（三明学院 信息工程学院，福建 三明 365004）

最近十年之间群智能优化算法已经成为优化领域中的研究热点，主要因为该算法具有灵活性强、无梯度机制和局部最优化等优点。群智能优化算法源于生物的集体行为，模仿大的种群如何寻找食物的方法。

蚁群优化算法(ant colony optimization,ACO)[1-2]和粒子群优化算法(particle swarm optimization,PSO)[3-4]是这类算法中较为经典的两类方法。ACO模仿蚂蚁寻找最短路径的社会行为，PSO模拟鸟群在飞行和狩猎中的行为。其他群优化算法有：2015年Karaboga等[5]提出的人工蜂群算法（artificial bee colony algorithm,ABCA），通过模仿蜜蜂采花蜜的行为进行寻优，该算法能够适应环境的变化；萤火虫算法（firefly algorithm,FA）[6]由Yang X S等[7]提出，通过模仿萤火虫的趋光性，向光源移动进行寻优；蝙蝠优化算法（bat algorithm,BA）是一种有效的全局搜索方法，该算法通过迭代搜索最优解，并且在最优解附近进行飞行产生局部新解，加强了局部搜索能力；2016年Mirjalili等[8]提出的鲸鱼优化算法（whale optimization algorithm,WOA）是一种模仿座头鲸捕食的算法，该算法在全局搜索及局部寻优均具有较强的能力。虽然进化优化与群体优化之间存在差别，但其共同点是能够在限定域中找到最优值。尽管各类算法都具有各自的优点，但No-Free-Lunch(NFL)定理[9]已经证明没有一种算法能够解决所有的优化问题。传统群优化算法无法解决所有优化问题，所以国内外许多学者研究改进原有的算法，增强其全局或局部搜索能力。刘佳等[10]提出了混合人工蜂群算法，在蜂群开采阶段加入全局搜索机制，提高了算法的搜索能力，解决了拆卸线平衡问题。杨景明[11]等提出了改进的多目标粒子群优化算法,引入了分解的思想，避免算法陷入局部最优，解决了文档分类的问题。Li Z[12]等提出了改进的飞蛾扑火算法，利用莱维飞行增加种群的多样性，防止局部最优发生，有效提高了算法的寻优能力。Dou R[13]提出应用莱维飞行加入元启发算法中，解决舰载机着陆控制问题，优化了自动驾驶仪的控制参数和功率补偿系统。诸多现有的群智能优化算法均存在一定的不足之处，但许多学者都一直在结合彼此特点进行取长补短，令改进后的群智能优化算法在全局搜索和局部寻优的能力尽量达到平衡统一，更好地解决工程应用中的寻优问题。

水波优化算法（water wave optimization，WWO）有着优秀的寻优能力，但是在解决工程问题时存在寻优能力不足。许多学者研究改进的算法对水波优化算法进行改进，金旭旸利用莱维飞行对水波算法进行改进[14],刘翱[15]利用自适应控制参数对水波算法进行改进,王万良[16]提出了模拟退火和水波算法的融合的优化算法,杜兆宏[17]提出了自适应参数对水波算法进行改进,顾启元[18]利用了自适应学习对水波算法进行改进,以上文献利用一种策略对优化算法进行改进，无法更好地平衡全局最优和局部最优。林伟豪[19]提出了自适应参数和动态分组学习策略对水波算法进行改进，有着较好的效果。顾启元[20]采用群自适应策略对水波算法进行改进，同时加入了约束调整，使优化算法的优化能力得到了提升。所以多种策略的合理使用可以显著地改善水波算法的优化能力。

本文为了解决传统水波优化算法在全局寻优能力较弱和收敛速度慢的问题，提出了利用莱维飞行和自适应权重两个方法，对经典的水波优化算法进行优化和改进，对单目标优化学习问题进行处理和研究，以提高原算法的精度和收敛速度为目标，在全局和局部两个方面引入不同策略进行完善，最终进行标准函数最优值的求解实验，进一步验证了所提出的改进算法的有效性。

1 改进的水波优化算法

水波算法主要模拟水波的传播、折射和分裂现象，有效地对搜索空间进行寻优[21]。水波在不同的深浅区域形成的波浪形状如图1所示。水波的运动过程是从深区到浅区，随着波高的增加，波长相应地随之减小，适应度函数值增大则增加[22-23]。

图1 水波模型

水波传播阶段:每个水波都会进行传播并且产生一个新的水波，其数学公式如式（1）

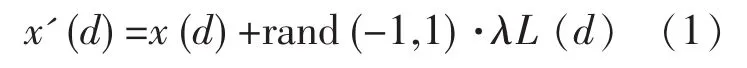
其中 L（d）为水波的搜索长度，rand（-1,1）是均匀分布的随机数。如果 f（x'）＞f（x），水波则会被新的水波x'取代。给出了一个水波的波长，如式（2）。

其中α表示水波波长约束因子;fmax，fmin分别表达所选择的适应度函数值的最大和最小值;ε可以选取为非零无穷小的正整数。

折射阶段:在波的传播过程中，波的能量持续下降，直到波高降为零，进行折射以避免搜索停滞。位置更新如式（3）

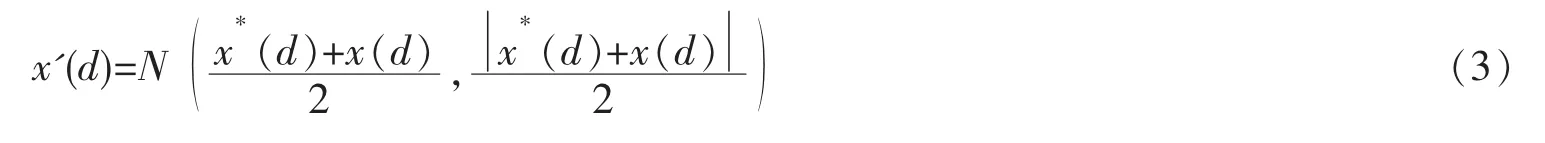
其中:x*为当前最优解;N（μ，σ）为生成的复合高斯分布的随机数。通过折射后，水波的高度会随着新的水波x'更新为hmax，并且波长更新公式如式（4）

分裂阶段:随着水波的传播，其携带能量也会逐渐增强，水波的波峰就会越来越陡峭，最后传播结束时水波就会最终分裂成多个独立的水波。为了模仿这个现象，随机选择k个维度，并且在每个维度产生一个单独的水波。单独的水波更新公式如式（5）

其中:β为水波分裂系数。

1.1 莱维飞行

莱维飞行最早是由Levy提出的，然后由Benoit Mandelbrot详细的对其进行描述[24-25]。实际上莱维飞行是一种随机步长描绘Levy分布的方法。大量的研究表明，自然界的很多动物和昆虫的个体行为表现就很好地表征了莱维飞行的基本特征。莱维飞行其本质是将步长随机化的模拟飞行的方法，图2是关于莱维飞行轨迹的模拟图像，它的步长总是很小，但是偶尔也会出现大的跳动。

图2 莱维飞行轨迹

莱维飞行的公式如式（6）

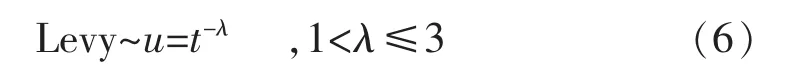
Mantegna提出的生成Levy随机步长的公式如式（7）

1.2 自适应权重

惯性权重因子是粒子群优化中的核心调节参数。当惯性权重较大的时候，会明显增强其搜索能力，大幅提升算法的搜索区域；当惯性权重较小的时候，算法后期的搜索能力会增强，可以提升局部寻优能力[26]。

水波算法进行局部寻优的时候以公式(2)向最优解逼近，但是局部寻优能力较弱。为了解决这个问题，提出了加入自适应权重这个参数，使得其全局和局部能力得到平衡。自适应权重公式如式（9）

其中:t为当前迭代次数;itmax为最大迭代次数。

1.3 改进的水波优化算法

经典的水波智能优化算法能够简单和高效地处理数学函数的低维单模优化求解问题，但采用相同的方法处理高维复杂的优化求解问题时，传统WWO所得到的解并不十分理想，而且运算时间长。为了提高WWO的全局搜索能力和局部探索能力，本文提出了一种改进的水波优化算法。Levy飞行可以最大限度地实现搜索域的多样化，这样能够保证算法高效地更新水波位置，实现局部最优；自适应权重系数能够加快算法的收敛速度，减少运算时间。通过上述改进思路能够看出利用莱维飞行和自适应权重系数有助于WWO获得更好的寻优结果，减少运算时间，因此对水波的位置更新公式做出优化，可用式（10）和（11）的数学公式进行表达。

改进后的算法能够大幅提高WWO的全局搜索能力从而避免进入局部最优值。这种方法不仅提高了WWO的搜索强度，也改善了算法的运行较长的问题。利用加入改进策略保证改进后的优化在避免陷入局部最优的前提下也能够准确找到函数的最优极值，通过增强多样性使该算法具有更好的全局搜索能力。同时该算法对单峰值、多模态的标准函数以及多阈值图像分割中的应用均具有较好的效果。通过上述分析可知，本文提出的改进水波优化算法IWWO(improved water wave optimization)的性能明显优于传统的WWO。

2 实验仿真分析

为更好地验证IWWO算法的有效性，本文以多种形式的标准数学函数进行算法测试，验证改进优化算法的优化求解能力和算法的运行效率。同时，与WWO,PSO和FPA(flower pollination algorithm)进行比较分析。

2.1 标准函数实验与分析

选取了多种标准函数作为测试函数来衡量元启发式算法的性能。测试函数的公式如表1所示，利用其不同函数的数学特性，从不同的角度来测试IWWO的性能[27]。表1为标准测试函数。测试函数大致可以分为三类：高维单模态测试函数、高维多模态测试函数、固定多模态测试函数，如图3所示。

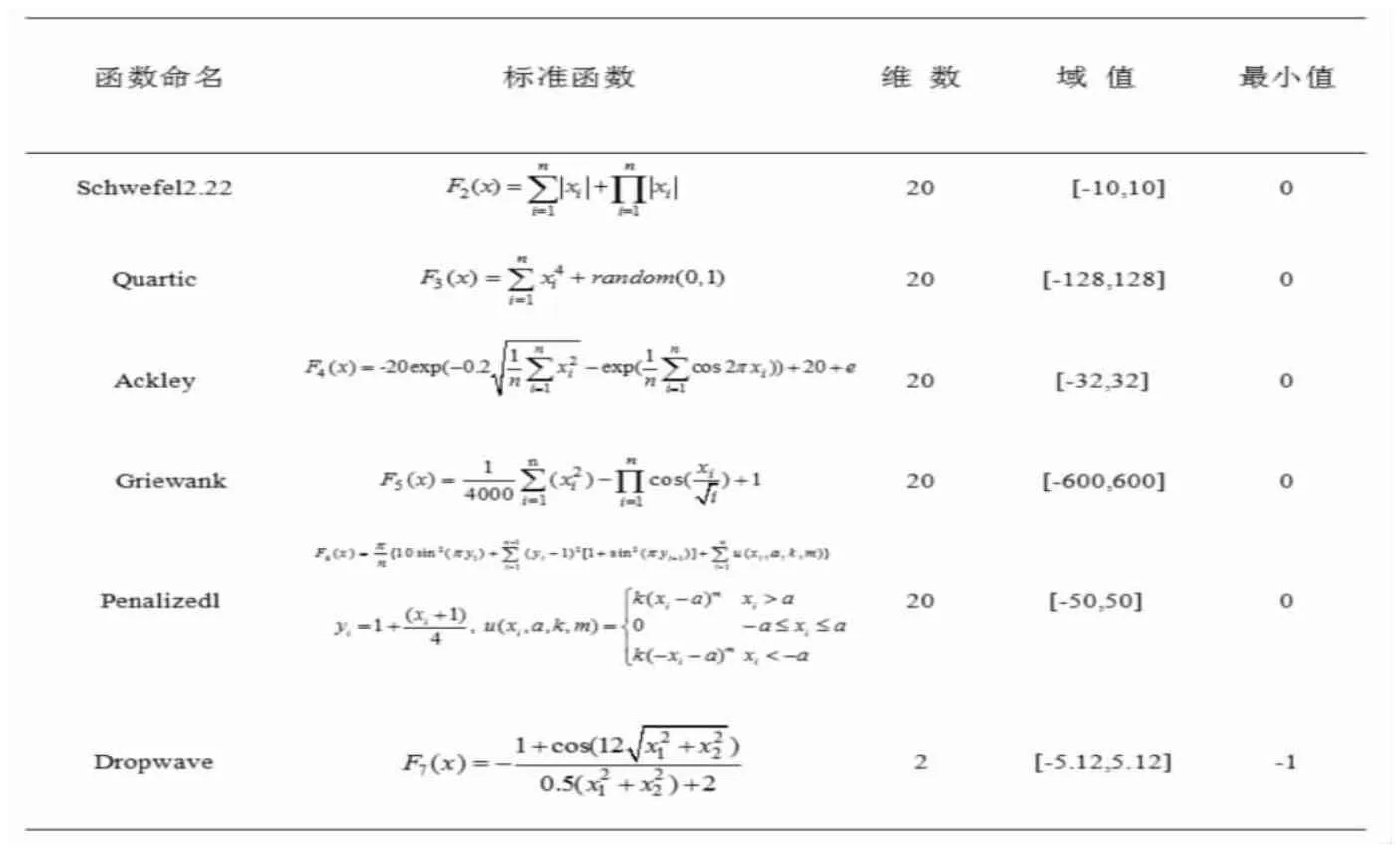
表1 标准测试函数

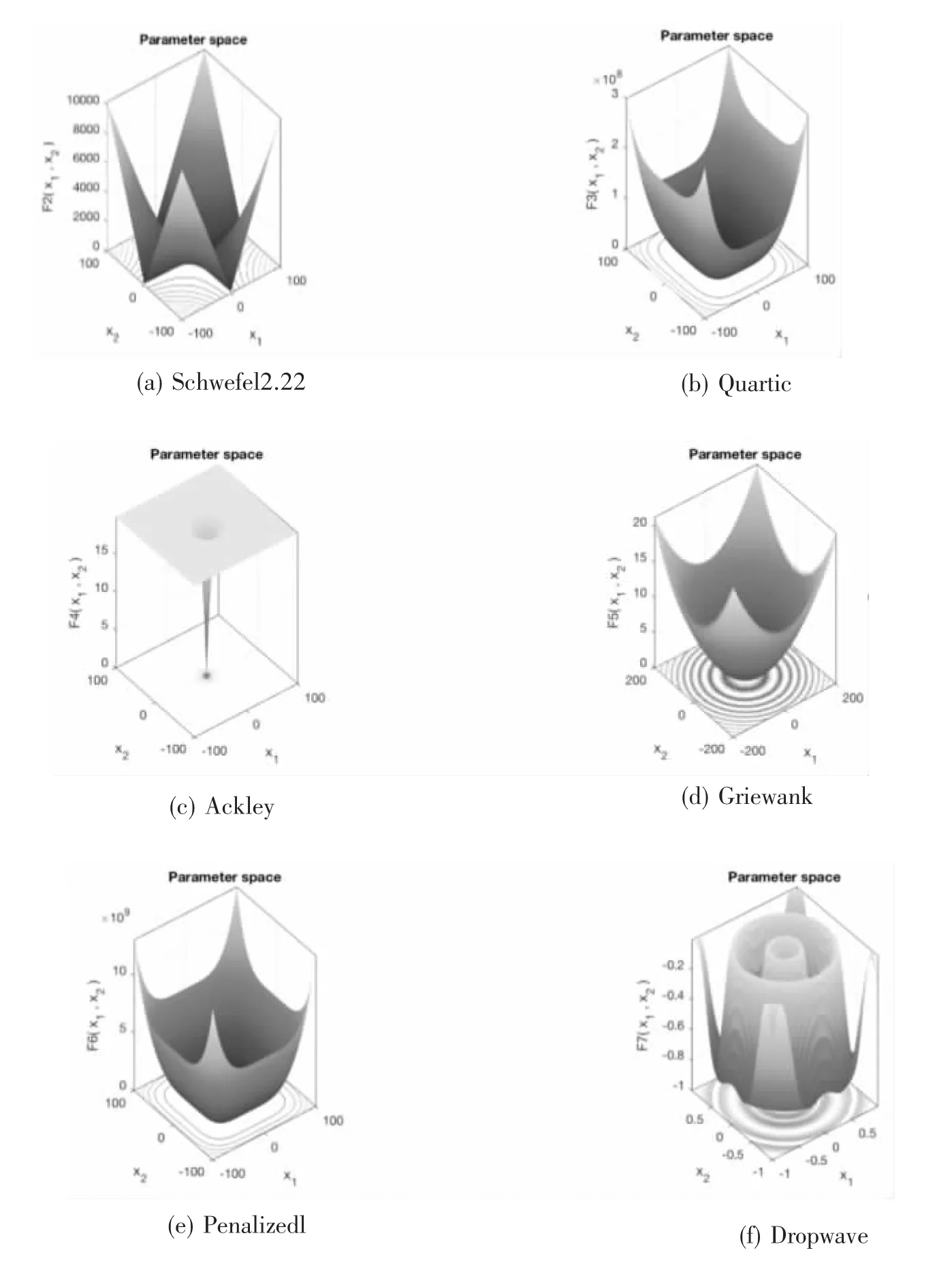
图3 标准测试函数效果图

图4清晰地给出了多种优化算法处理表1中标准函数寻优后最优值的收敛曲线，从收敛曲线的走势能够明显看出改进后的水波算法同时兼具精度高和收敛速度快的两类优点，函数寻优的最终结果均优于对比的其他几种传统优化算法。这也进一步说明了IWWO算法具有更强的局部搜索能力，且不会产生陷入局部最优的问题，选择的两种策略很好地平衡了全局大范围搜索和局部小范围寻找最优解之间的关系，准确地找到了备选测试标准函数的理论极值。

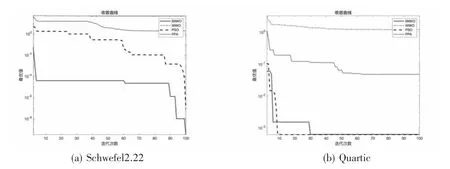
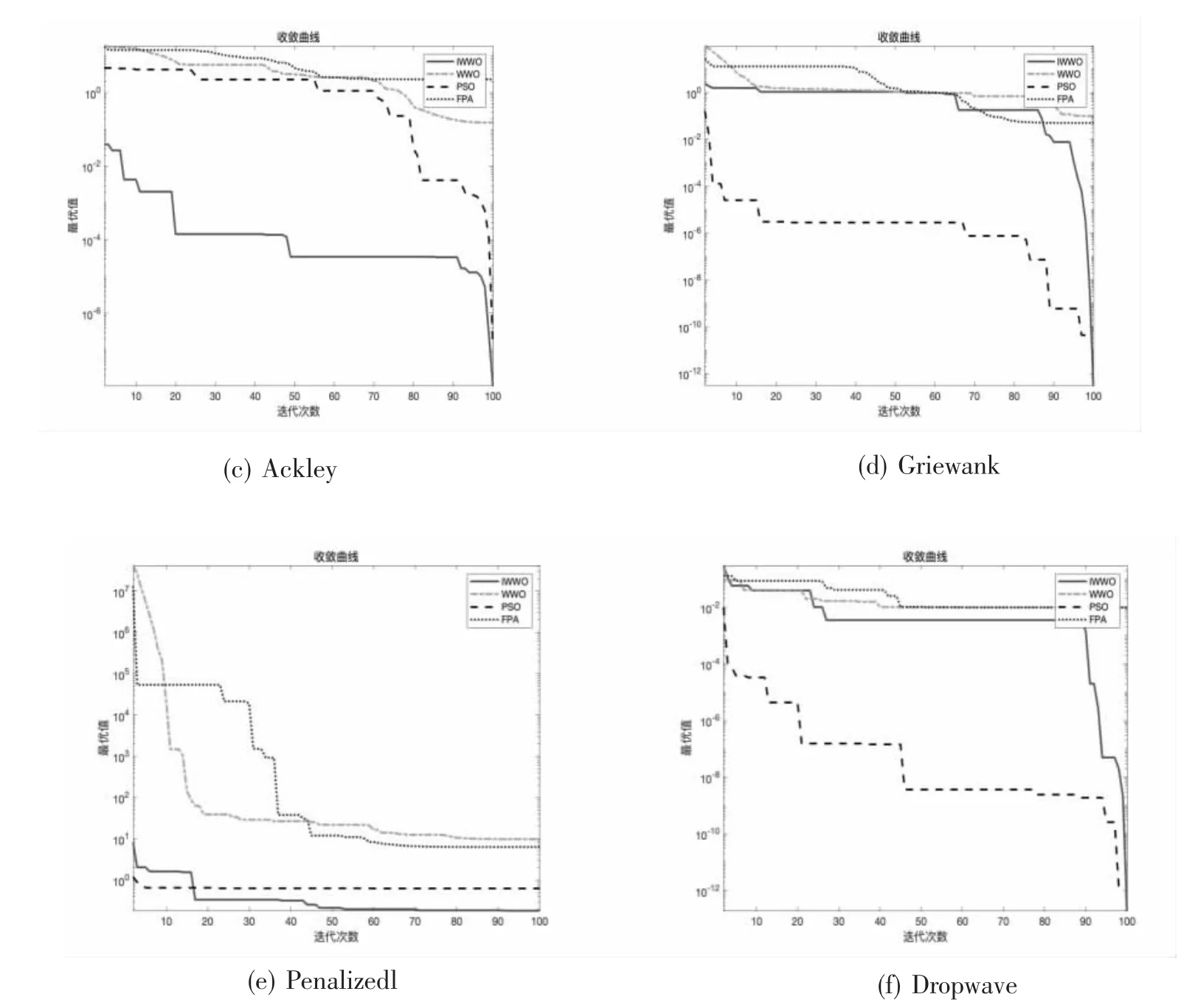
图4 各算法的收敛曲线

为了进一步对IWWO的优越性进行评价和测试，将本文选择研究对比的智能优化算法均独立运行30次，验证每个选择算法的稳定性，如表2所示给出了相应的实验结果。由表2可知，IWWO的算法的AVE和Std波动不大。同时，从表中结果可知在所有实验结果中，IWWO算法有5个结果优于其它算法，PSO算法有1个结果优于其它对比算法，所以IWWO算法优于其它对比算法。说明IWWO算法不仅具有优秀的寻优能力，同时能够稳定地进行寻优。

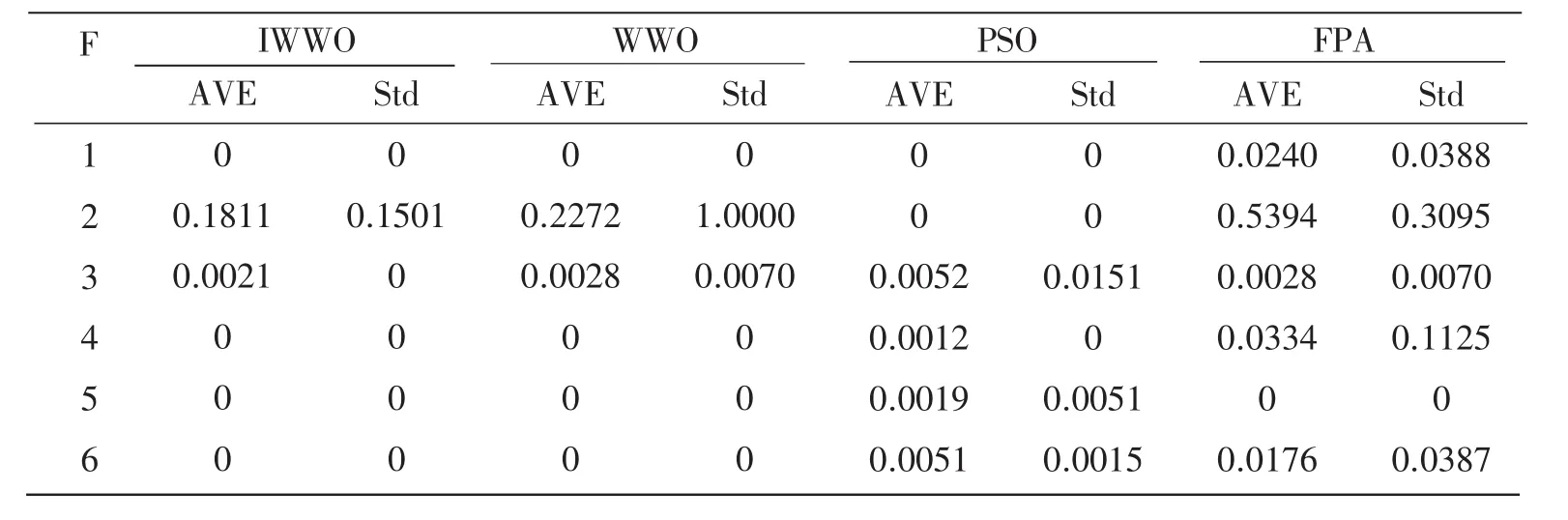
表2 各算法运行的稳定性

3 结束语

本文在研究了基于莱维飞行和自适应权重的水波优化算法之后，获得3个主要结论。

(1)提出一种基于莱维飞行和自适应权重的水波优化算法，该方法采用莱维飞行算法改进水波的传播机制，利用其随机移动机制使水波向最优值移动。

(2)加入自适应权重因子使水波分裂阶段更集中，加强对局部区域的探索能力，保证算法的收敛能力。

(3)选择经典的标准函数进行优化仿真测试，很好地验证了改进优化算法的寻优求解能力，最优值以及稳定性明显优于WWO、PSO和FPA算法，充分验证了所提出的算法的优化能力。