双排抗滑桩加固滑坡的前桩后侧推力算法

闫玉平，肖世国

（1.西南交通大学地球科学与环境工程学院，四川 成都 610031；2.西南交通大学高速铁路线路工程教育部重点实验室，四川 成都 610031）

双排全长桩或后排沉埋-前排全长桩越来越多应用于大型基覆式滑坡的治理工程[1−6]，如图1所示，d0=0与d0>0分别表示前排全长与后排沉埋桩。对于此类问题，两排桩上推力大小及分布模式是工程设计中的关键因素之一。

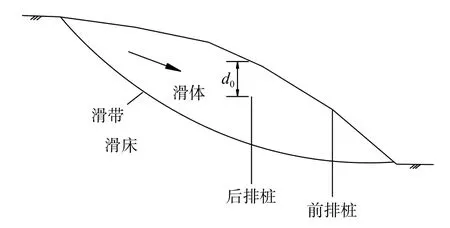
图1 双排桩加固滑坡横截面示意图Fig.1 Sketch map of the cross section of a landslide reinforced with double-row piles

后排桩上推力求解类似于单排桩，以往已有较多计算方法[7−13]。中铁二院曾对单排桩上推力进行现场模型试验[14−16]，得到了其分布模式。也有学者通过室内模型试验对沉埋桩及后排沉埋-前排全长桩后侧推力进行研究[17−19]，确定了试验模型桩后推力作用特征。郑颖人等[20]、赵尚毅等[21]、宋雅坤等[22]则采用有限元方法得到了单排全长抗滑桩或沉埋桩的受力特征。

在前排桩后侧推力的解析计算方面，刘鸿[23]、李明康[24]采用弹性理论对双排抗滑桩排间岩土体的传力机制进行了分析，得出了前排桩后侧推力的表达式，但对排间岩土体，其采用弹性分析模型偏于理想化；肖世国等[25]基于后排桩推力向前传递的地基系数“k”法以及排间岩土体推力传递的传递系数法，提出了一种计算前排桩后侧推力的方法，但不能给出前排桩上推力分布模式，且采用滑体侧向抗力系数沿深度不变的模式也尚需优化；杨磊[26]将弹性理论与条分法相结合，以此可近似得到前排桩上推力，但该法关于条块间正应力分布模式呈抛物线形或直线型的假设仍存在不合理性。总之，上述这些求解前排桩上推力的方法有下面两个明显缺陷：（1）模型过于理想化；（2）无法兼顾推力大小与分布模式。

针对既有方法的不足，为了在求解前排桩后侧坡体推力的同时也可得到其分布模式，以便更合理确定前排桩受力特征，本文采取如下基本思路：首先，考虑滑体侧向抗力系数随深度变化的实际情况，采用地基系数“m”法求得后排桩受荷段前侧滑体抗力；然后，考虑双排桩排间滑面特征，采用平行于滑面的斜条分法对排间土体进行分析，将排间土体分割为若干斜条，根据各条块应满足的静力平衡条件，同时确定作用于前排桩受荷段后侧的推力大小及其分布模式。

1 计算方法

对于双排桩加固滑坡的排间滑体，其基本分析模型如图2所示，将其后边界OC与前边界DE之间的滑体以平行排间滑面方向分割成n+1条，边界OC与DE自上而下的分割点分别依次标为点A0，A1，···，An−1和点D1，D2，···，Dn−1。图2中，d0为后排桩沉埋深度，当d0=0时，表示全长桩；d为后排桩受荷段长度；s为前后排间距；s0为排间滑面折点F距后排桩距离；q1、q1+q2分别为边界OC顶、底端的水平压力；α1、α2分别为排间滑面段CF、FE的水平倾角；e1、i、n为条块编号。

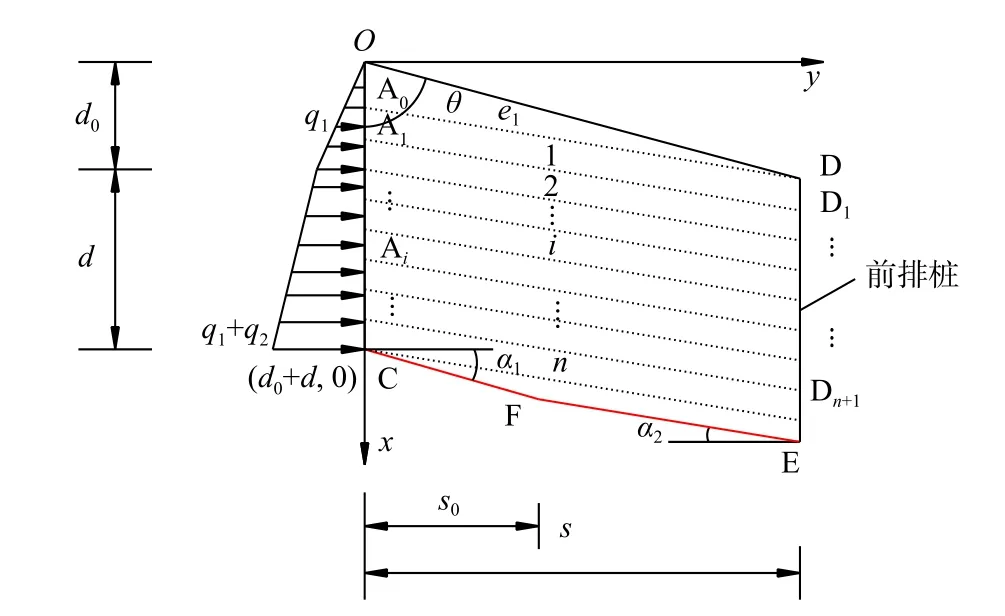
图2 排间滑体基本分析模型Fig.2 Basic analytical model of slide mass between two rows of piles

对于排间滑面CE，这里考虑存在一个折点F的情况。当α1=α2时，退化为直线型滑面；对于排间滑面多折点的情况，求解方法类似于一个折点情况，不再赘述。为简化分析，作如下假定：

（1）后排桩受荷段前侧土体的抗力在后排桩全长与沉埋时，分别为三角形、两段折线形分布。

（2）各斜条块假设为刚体，且条块之间相互作用力、前排桩作用于各条块的力、滑床对最下面一个条块的作用力均位于相应作用面的中点，由此可得各典型条块受力分析模型如图3所示。

（3）前排桩作用于第i条块的切向力Tpi和法向力Npi之间满足Tpi=kpNpi，其中kp为桩土界面综合参数。

（4）两排桩之间的滑面处于极限状态且满足Coulomb强度准则。

记排间滑体重度、内摩擦角、黏聚力分别为γ、φ、c，对图3所示的不同深度处典型条块分别进行受力分析。

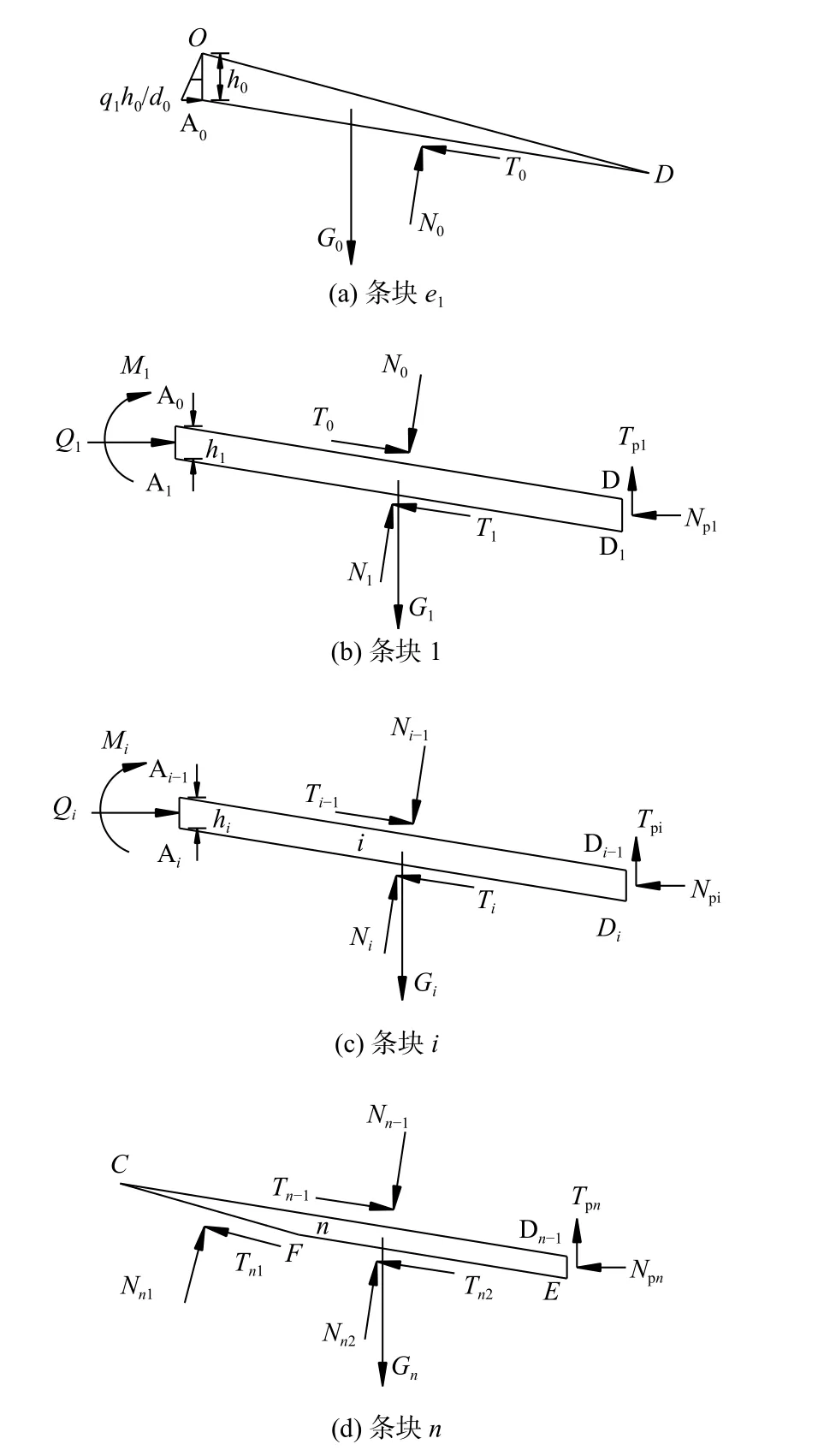
图3 各典型斜条块受力分析模型Fig.3 Mechanical analysis model of each typical oblique slice

1.1 顶部条块e1

对于三角形条块e1，只包含其下表面上的切向力T0和法向力N0共2个未知力，需满足水平和竖向静力平衡方程，即：

式中：h0—条块左侧长度；

G0—条块e1的重力，G0=γsh0/2；

l0—条块e1底面长度。

根据Coulomb强度准则，还应满足：

求解方程（1）可得：

1.2 位于d0范围的平行四边形条块

此范围内各条块分析方法相同，以条块1为例具体阐述。以条块1下表面上的切向力N1和法向力T1作用点位置为矩心，由静力平衡条件及假定（3）可得：

式中：Q1—条块1左侧水平方向合力；

M1—左侧作用力产生的力矩；

G1—条块1的重力。

可分别表示为：

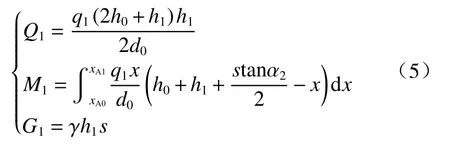
式中：h1—条块1左侧长度，条块2～n-1标记以此类推；下文中Ni、Ti的含义同条块1。

由式（4）可推导得到：

对位于d0范围内的其他条块k，只需要将方程（6）中的下标1换为k，将0换为k-1即可，而其中的Qk、Mk、Gk则按方程（7）求解：

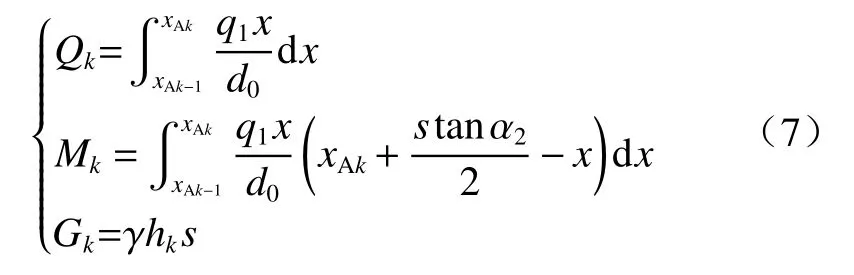
1.3 位于d范围内的平行四边形条块

对位于d范围内的条块i，其受力分析模式同条块1，因此只需将方程（6）中下标1换为i，将0换为i-1即可。但该范围内Qi、Mi解法因左边界荷载不同而与d0范围内情况略有不同，其求解方程为：

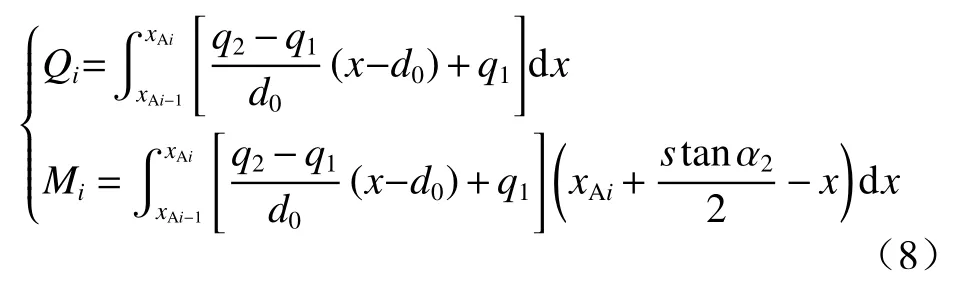
1.4 底部条块n

设该条块面积为Sn，则其重力为Gn=γSn；以Tpn和Npn作用点位置为矩心，由静力平衡条件及假定（4）可得：

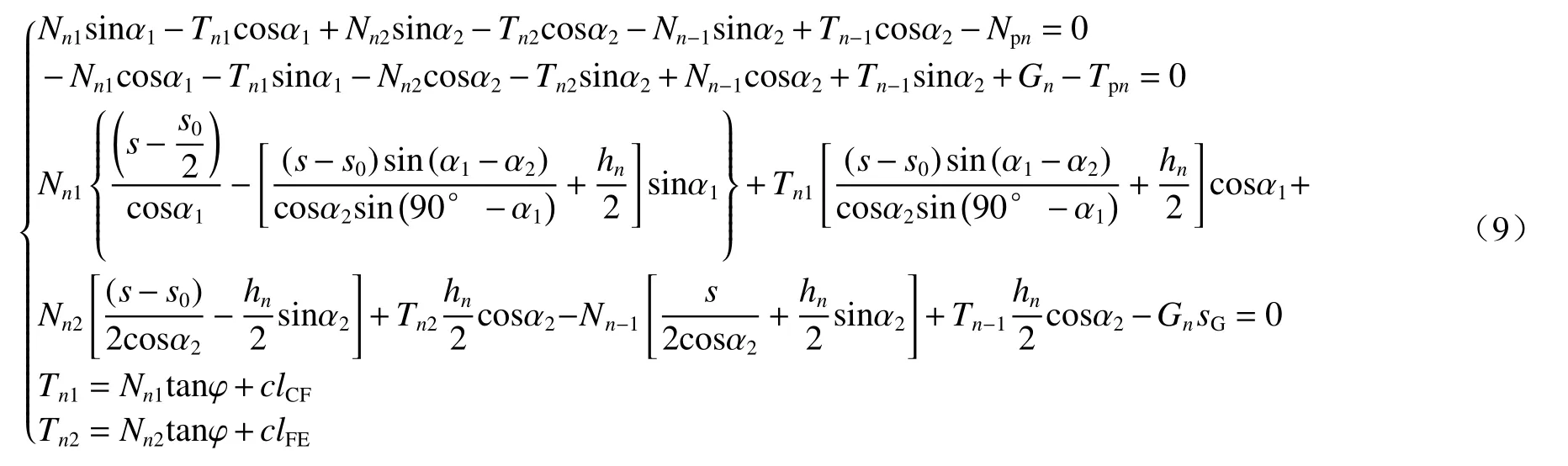
式中：sG—条块n的形心位置距右侧的水平距离，

Nn1、Tn1—条块n底面CF上的法向力和切向力；

Nn2、Tn2—条块n底面FE上的法向力和切向力；

hn—条块n右侧长度；

lCF、lFE—底面CF、FE的长度。

由式（9）可得关于Nn2、Npn的二元一次方程组为：

式中中间变量η1、η2、η3、η4和χ1、χ2、χ3、χ4表达式分别为：

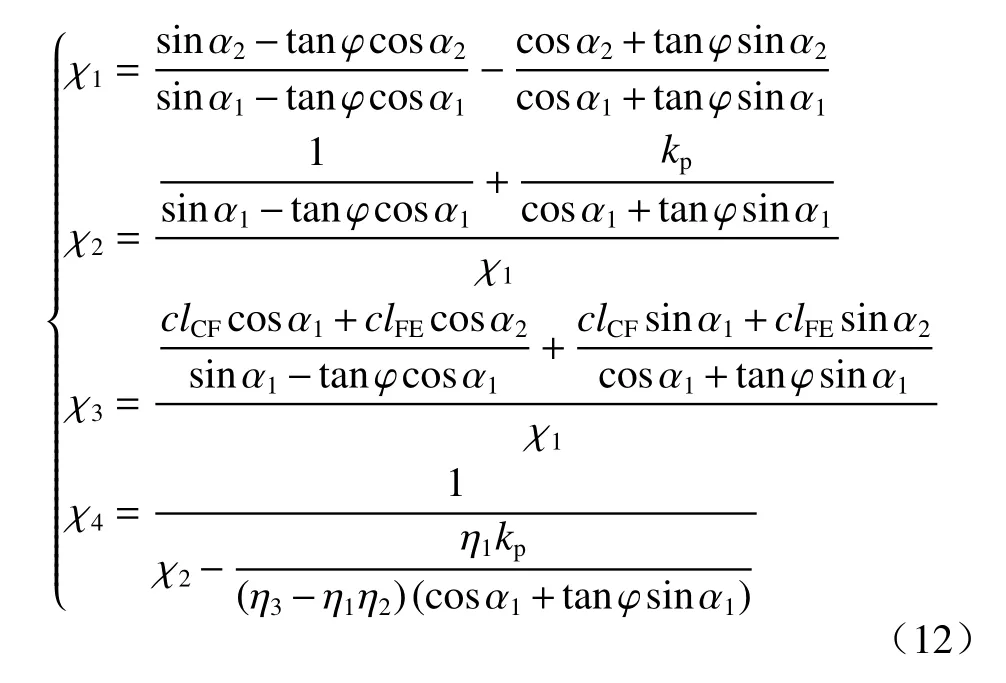
于是，由式（10）可得Npn、Nn2的表达式分别为：

将式（13）（14）代入式（9），可确定Tn1、Tn2、Nn1及Tpn。

通过上述求解方法，可得各条块对前排桩的作用力（局部作用力），因此将其叠加可得前排桩所受的合推力，即：

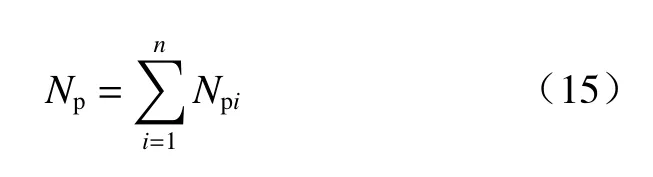
2 实例分析

西南地区某铁路工程沿线存在一中风化大理岩上覆碎石土堆积体的潜在滑坡，滑坡主轴横断面示意图如图4所示，通过现场勘查与试验，确定坡体主要物理力学参数如表1所示。利用传递系数法[27]求得天然工况下该坡体稳定系数为1.128。拟采用双排抗滑桩加固，桩体采用C30混凝土浇筑，截面尺寸为2 m×3 m，桩间距（平面外）为5 m。前排桩拟设于距坡脚水平距离约30 m的滑面平缓地段，后排桩则分别考虑距前排桩水平距离25 m和45 m 2个位置，同时也考虑后排桩顶沉埋情况，故拟定4种设桩方案。

图4 双排抗滑桩加固滑坡实例横截面图Fig.4 Cross section of a practical landslide reinforced with double-row stabilizing piles

表1 坡体及抗滑桩主要物理力学参数Table 1 Main physical and mechanical parameters of the landslide and piles

方案一：后排桩位于桩位一，桩顶位于坡面；

方案二：后排桩位于桩位二，桩顶位于坡面；

方案三：后排桩位于桩位一，桩顶埋深7.4 m；

方案四：后排桩位于桩位二，桩顶埋深7.0 m。

在设计安全系数为1.20的情况下，利用传递系数法及地基系数“m”法[27]求得各方案时后排桩对其前侧滑体的推力分布如图5所示。

图5 4种设桩方案对应的排间滑体计算模型Fig.5 Calculation models of slide mass between two piles corresponding to four design plans in the example

采用前述斜条分法，求解作用于前排桩受荷段后侧的坡体推力。各设桩方案相应的排间土体条分模式见图6，前排桩土界面综合参数kp取为tanφ[28]。

图6 4种设桩方案对应的条分模式Fig.6 Slice modes of slide mass between two piles corresponding to four design plans in the example

表2给出了各方案时相应各土条对前排桩的局部推力Npi及其合推力值。可见，对于后排全长桩的方案一和方案二，其前排桩推力计算值比较接近，方案一（排间直线型滑面）较方案二（排间折线型滑面）的推力值偏大约5%。同时，当排间滑面为直线型时（方案一和方案三），方案三（后桩埋深7.4 m）较方案一（后桩全长）的前排桩推力值偏小约10.6%；当排间为折线型滑面时（方案二和方案四），方案四（后桩埋深7.0 m）较方案二（后桩全长）的前排桩推力值偏小约8.6%。此外，所拟定的4种方案中，方案四时作用于前排桩后侧的推力最小。方案一和方案二的前排桩推力值均大于后排沉埋桩的方案三和方案四，这也反映出后排桩沉埋有利于减小前排桩后侧推力。其原因在于后排桩沉埋时作用于排间滑体后侧的推力有所减小（图5）。

对表2中所示的各土条对前排桩的局部推力值除以其相应作用面积，可近似得到该条处前排桩后侧的压应力，进而可得前排桩受荷段后侧推力分布模式如图7所示。

表2 在4种设桩方案下各土条对前排桩局部推力及其合推力Table 2 Local thrusts by each slice and their resultants on the fore piles under four design plans/（kN·m−1）

由图7可见，各设桩方案时前排桩后侧推力分布模式较为相似，均呈不规则的抛物线型分布。桩顶局部范围内桩后压应力有先减小再增大的特征，最大压应力位于距受荷段底端高0.11～0.17倍受荷段高度，其下至滑面处桩后压应力急剧减小至近于零。

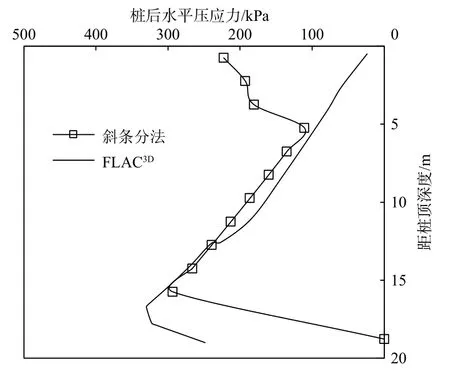
图7 4种设桩方案下前排桩受荷段推力分布曲线Fig.7 Distribution curves of thrust on the fore piles under four design plans in the example

3 对比验证

为了进一步说明本文方法的合理性，以前述实例中的设桩方案四为例，采用FLAC3D进行数值模拟分析，与理论计算结果予以比较。所建数值模型如图8所示，模型含72 198个8节点6面体单元，坡体采用服从Mohr-Coulomb屈服准则和关联流动法则的理想弹塑性本构模型，桩体视为弹性材料，利用结构单元模拟。模型前后左右四个边界进行水平位移约束，底面同时进行水平和竖向位移约束。采用强度折减法进行数值模拟分析，得到该滑坡模型的稳定系数为1.12，与前述的传递系数法计算结果基本一致，说明数值模型有一定的合理性。

图8 实例方案四的双排抗滑桩加固滑坡数值模型Fig.8 Numerical model of the practical landslide reinforced with double-row piles under the fourth design plan

图9为数值模拟得到的加固后滑坡的水平应力分布云图，由此可得前排桩后压应力分布图，如图10所示。可见，在桩顶以下局部约0.25倍受荷段高度范围以内，理论计算与FLAC3D模拟所得的桩后压应力分布有差异，前者沿深度呈非线性减小模式，后者则为近似线性增大模式，且后者整体小于前者，意味着理论计算偏于保守；在此局部范围以下，两种方法得到的桩后坡体压力变化规律基本一致，均为先近似线性增大，近滑面处达到极大值，然后再急剧减小；二者得到的桩后峰值压应力偏差约10%，理论算法略小于数值模拟结果。

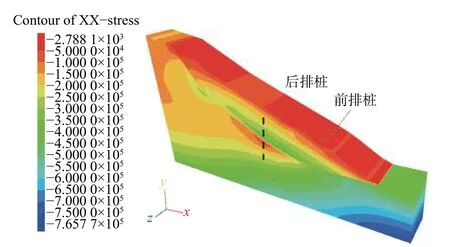
图9 实例方案四加固坡体的水平应力分布云图Fig.9 Contour of horizontal stress of the reinforced landslide using the fourth design plan in the example

图10 实例方案四时前排桩后侧推力分布模式对比Fig.10 Comparison of distribution patterns of thrust on the fore piles under the fourth design plan in the example

表3给出了传递系数法、FLAC3D模拟法和本文的斜条分法得到的4种设桩方案时的前排桩受荷段后侧坡体推力值。可见，本文方法比传递系数法的结果分别偏大约10.6%、12.5%、11.5%、13.4%，而比FLAC3D结果分别偏大约13.2%、7.95%、1.31%、−0.72%。因此，相对于传递系数法，本文方法整体更接近于FLAC3D计算结果。

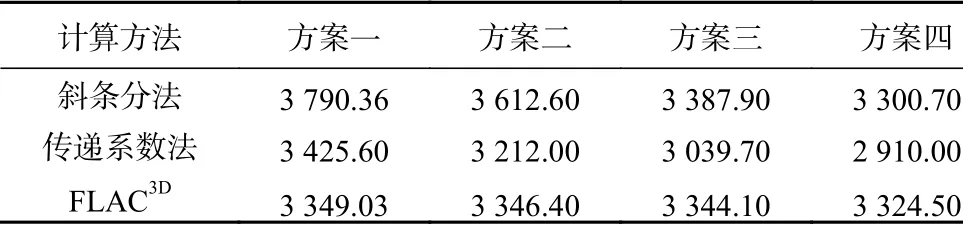
表3 不同方法求得的4种设桩方案下前排桩上推力值对比Table 3 Comparison of thrust on the fore piles under four design plans by various methods/（kN·m−1）

4 结论

（1）前排桩后侧推力呈不规则的抛物线形分布，其峰值点位置接近滑面，在峰值点以下，受荷段桩后坡体压力急剧减小至接近于零。

（2）对于后排桩沉埋模式的双排桩，前排桩后侧坡体推力小于后排桩全长模式的结果。本文方法实例计算表明，前者比后者偏小8.6%～10.6%。

（3）本文提出的斜条分法与传递系数法、FLAC3D数值模拟方法计算的前排桩后侧坡体推力值较为相近，本文方法整体较既有两种方法均偏大，结果偏于保守一面。实例分析表明，本文方法比传递系数法结果偏大10.6%～13.4%，且相对更接近于FLAC3D数值模拟结果。