考虑侧壁土体脱离影响的桶基承载力
程健 姜君 王栋

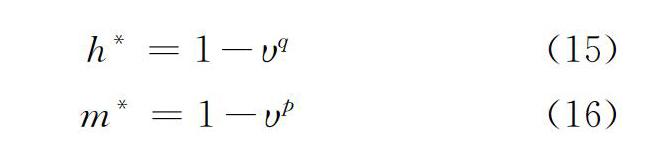

摘 要:當桶基发生平动或转动,其侧壁可能与土体发生脱离,形成空隙,土体破坏模式由“双侧式”变为“单侧式”,承载力降低。建立桶基与黏性土相互作用的三维有限元模型,设置允许脱离和不允许脱离两种接触类型,改变土体强度和桶基长径比,确定桶基与土体发生脱离的条件,探讨脱离对桶基承载力的影响,总结单向与复合加载的承载力公式。结果表明:当允许桶基与土脱离时,土体强度越高,单向与复合承载力降低越严重,但长径比对承载力降低程度影响不大。对于单向承载力,建议通过折减系数量化脱离的影响;对于复合加载,提出了同时适用于允许和不允许脱离的归一化包络面表达式。
关键词:桶基;承载力;脱离;有限元;黏土
中图分类号:TU470 文献标志码:A 文章编号:2096-6717(2020)04-0052-06
收稿日期:2020-10-25
基金项目:国家自然科学基金(41772294、U1806230、42025702)
作者简介:程健(1994- ),男,主要从事海洋岩土工程研究,E-mail:chengjian@stu.ouc.edu.cn。
王栋(通信作者),男,教授,博士生导师,E-mail:dongwang@ouc.edu.cn。
Received:2020-10-25
Foundation items:National Natural Science Foundation of China (No. 41772294, U1806230, 42025702)
Author brief:CHENG Jian (1994- ), main research interest: offshore geotechnical engineering, E-mail: chengjian@stu.ouc.edu.cn.
WANG Dong (corresponding author), professor, doctorial supervisor, E-mail: dongwang@ouc.edu.cn.
Capacities of bucket foundation considering the influence of sidewall-soil separation
CHENG Jian, JIANG Jun, WANG Dong
(College of Environmental Science and Engineering, Ocean University of China, Qingdao 266100, Shandong, P. R. China)
Abstract: When the bucket foundation moves laterally or rotates, its sidewall may be separated from the soil to form a gap. The failure mechanism of the soil changes from "double-sided" to "single-sided", which reduces the bearing capacity. The three-dimensional finite element model was established to simulate the reaction between bucket foundation and cohesive soil. Two different types of contact types were set up, allowing separation or not allowing separation. The soil strength and aspect ratio of the bucket foundation were varied to determine the conditions when separation occurs. The effect of the separation on the bearing capacity of the bucket foundation under different conditions was studied, and the capacity formulas of uniaxial and combined loading have been proposed. The results show that the separation of the bucket foundation from the soil reduces the uniaxial and combined bearing capacity, and the reduction is more significant with the increase of soil strength, while the aspect ratio has little effect on the reduction of bearing capacity. For uniaxial bearing capacity, it is recommended to quantify the impact of separation through the reduction factor. For combined bearing capacity, the normalized envelope surface expression that is suitable for both separation and not separation situations has been proposed.
Keywords:bucket foundation; bearing capacity; separation; finite element method; clay
负压桶基础广泛应用于海洋工业,如作为管道终端的支撑基础、张力腿平台的锚泊基础以及海上风机基础等[1-3],本质上是一种底端敞开、上端封闭的裙式基础(图1)。安装负压桶时,由桶顶向外抽水,在桶内形成负压,将桶基压入土中。桶形基础根据材料可分为钢质和混凝土桶基,壁厚范围通常在0.012~0.5 m之间[4-5]。与海上风电常用的单桩基础相比,桶形基础具有埋深浅、施工快捷、可回收等优点[6-7],更适用于基岩上覆土层厚度有限的地层,如中国福建和广东部分海域,这些地区的基岩上仅覆盖了10~30 m厚的软土层。桶形基础用于支撑固定式风机,承受的复合加载包括:自重和上部结构重力、上部结构传递的水平荷载和弯矩[8]。
现有研究大都假设正常工作状态的桶基外侧壁与土体保持接触、不发生脱离[9-11],但Randolph等[12]、Guo等[13]以及Kumar等[14]的试验表明:较大水平力作用下桶基背侧可能与土体分离,土体破坏模式由双侧式变为单侧式,使得水平承载力降低。按照DNV规范[15],桶基承载力取决于桶基侧壁是否与土体发生脱离形成空隙。桶基沉贯经常形成侧壁与土体之间的缝隙,荷载作用下吸力难以充分发展,此时的桶基承载力计算需要考虑侧壁与土体可能脱离。
对于承受斜拉荷载作用的桶基,比较“桶土”接触与脱离两种条件,正常固结黏土中后者的斜拉承载力最多比前者低11%,而超固结土中可达27%[16]。目前还不清楚竖向压力和水平力共同作用下“桶土”脱离造成的影响。Gelagoti等[17]发现,“桶土”保持接触时单向水平承载力或抗弯能力显著高于允许脱离时,但该研究仅针对不排水强度不随深度变化的超固结土,而正常固结或弱超固结海洋黏土的不排水强度大多随深度线性增加。
笔者利用有限元软件Abaqus,研究正常固结土中“桶土”接触条件对单向和复合承载力的影响,同时,考察桶基长径比、土体强度等因素与接触条件的耦合作用,最终提出“桶土”脱离时的单向和复合承载力计算方法。
1 建立有限元模型
建立三维有限元模型模拟桶基与土体的相互作用。桶基刚度远大于土体,因此,假定桶基为刚体。试算和以往研究[18-19]均表明,归一化的承载力与桶基直径无关,此处取桶径D=10 m;桶长L=10、15、20 m,即长径比L/D=1、1.5、2,这也是近海风机桶基的典型尺寸;桶基壁厚取为t=0.2 m;桶形基础的截面积用A表示。以桶基顶面中心点为参考点,上部结构传递的竖向荷载V、水平荷载H和弯矩M施加在参考点上,参考点的竖向位移为w、水平位移为u、转角为θ。由于竖向承载力基本不受脱离影响,所以,单向承载力部分仅考虑脱离对水平承载力和弯矩承载力的影响。
由于桶基具有几何对称性,三维模型中只需考虑一半的基础和土体,以提高计算效率(图2)。土体范围为:径向由桶基侧壁向外延伸3D,竖向由桶基底部向下延伸3L,此计算区域已足够消除边界效应。采用三维八节点六面体全积分单元剖分土体,为确保计算精度和计算的收敛性,加密桶周及桶内土体,加密区域单元尺寸为0.1D。
采用Tresca理想弹塑性模型描述不排水条件下的海洋黏土,正常固结土的不排水抗剪强度su随深度线性增加。
su=sum+kz(1)
式中:sum为土体表层的不排水抗剪强度,k为不排水强度随深度增加的坡度;z为土体深度。取典型值sum=1、8、15 kPa;海洋黏土的k大致在1~1.5 kPa/m之间,取上下限k=1.5、1 kPa/m。为近似模拟土体不排水条件,令泊松比为0.49。土体弹性模量E对极限承载力影响很小,为提高计算效率,取E/su=10 000。土体有效重度γ′=6 kN/m3。
设置两种不同的“桶土”接触类型:1)桶基与土体不发生任何相对运动,桶内外侧壁与土体之间采用tie连接。2)允许桶基与外侧土体发生分离,桶外侧壁与土体为摩擦接触,接触面上的最大剪切应力为sum+kL/2。由于桶内土体会随着桶基一起运动,所以,桶基内壁与土体之间仍采用tie连接。
2 有限元模型验证
首先与已有结果[16-17]进行对比,以验证建立的有限元模型的可靠性。Gelagoti等[17]的有限元分析针对均质黏土:su=60 kPa,L/D=0.2~1;按位移控制模式施加水平力或弯矩,竖向荷载V=0;在施加水平位移或转角时,约束另一个荷载分量。笔者采用相同参数,但将长径比扩展到L/D=0.2~2。当L/D<1时,计算结果与文献[17]非常接近,如图3所示,两种“桶土”接触类型得到的承載力差别均小于5%。
对于承受斜拉荷载作用的VH复合加载情况,与Supachawarote[16]的有限元结果进行比较(图4)。其中D=5 m,L/D=3,su=(10+1.5z) kPa,有限元模型中参考点选在0.65L深度处的桶体中心。计算结果与文献[16]的有限元结果接近,最大误差为6%。
3 单向承载力
对于竖向加载、水平加载或施加弯矩等单向加载情况,采用位移控制模式在参考点上施加位移或转角,此时不约束其他位移分量。由于规定土体刚度较大,“水平反力位移”曲线或“弯矩转角”曲线均很快达到稳定值,该稳定值即为单向承载力。
采用与文献[19]类似的承载力表达形式,但重新拟合各参数在不同工况下的取值,总结了不允许脱离时单向竖向承载力Vt0、单向水平承载力Ht0和单向抗弯能力Mt0的表达式
Vt0=πDLsuav+AsutipNcV(2)
NcV=9.73+0.4(L/D-1)(3)
Ht0=DLsutipNcH(4)
NcH=nH(mHkL/sutip+1)(5)
nH=4.27(0.22(L/D)2-0.76(L/D)+1.8) (6)
mH=0.05(L/D)2-0.32(L/D)-0.29(7)
Mt0=D2LsutipNcM(8)
NcM=nM(mMkL/sutip+1)(9)
nM=2.76(0.18(L/D)2+0.16(L/D)+0.8) (10)
mM=0.04(L/D)2-0.32(L/D)-0.12(11)
式中:suav=sum+kL/2。
“桶土”脱离与否对竖向承载力影响很小,但可能显著影响水平承载力与抗弯能力。允许脱离时,水平荷载或弯矩作用下土体的破坏模式相似,因此,以水平加载为例,展示桶基周围土体位移。取L/D=1,图5显示了土体强度影响“桶土”之间空隙的形成。当k=1 kPa/m时:1)如果sum=1 kPa,桶基外側和土体之间不会形成空隙,这是由于土体浅层强度较低,即使允许脱离,土体也会随着桶基一起运动,左右两侧对称的楔形土体被激发平动,桶底截面以下一定深度范围内的土体也被带动旋转(图5(a)),桶基的转动中心在中心轴附近。2)如果sum增大到8 kPa,浅层土体强度达到了可以保持直立的程度,桶基背侧和土体之间形成空隙,土体的破坏模式由对称的楔形破坏转变为单侧破坏,但底部土体的破坏模式及旋转中心的位置基本不改变(图5(b))。增大k至1.5 kPa/m,发现k值的改变基本不会影响土体的破坏模式,因为空隙一般出现在深度较浅的土体区域内,因此,影响土体破坏模式的关键因素是sum。
定义折减系数βh和βm表示脱离对水平承载力和抗弯能力的影响。βh=Hs0/Ht0,Hs0为允许脱离时的水平承载力;βm=Ms0/Mt0,Ms0为允许脱离时的弯矩承载力。通过归一化参数sum/kD表征sum和k对承载力的影响。进行多组变动参数分析,拟合不同土体强度及长径比条件下单向水平承载力和抗弯能力的变化,得到
βh=1-sum/kD2.77sum/kD+1(12)
βm=1-sum/kD4.18sum/kD+1.68(13)
公式计算结果与有限元计算结果比较见图6。随着sum/kD的增加,承载力降低程度逐渐变缓,这是因为“桶土”之间空隙的形状不再改变。与不允许脱离相比,允许脱离时的水平承载力最多减少28%,抗弯能力最多减少20%。同时,长径比不显著影响承载力降低程度。利用式(4)~式(11)计算不允许脱离时的Ht0和Mt0,分别乘以式(12)和式(13)给出的折减系数,即可获得允许脱离时的单向承载力Hs0和Ms0。允许脱离时的竖向承载力Vs0按式(2)计算。
4 复合承载力
对于竖向荷载V、水平荷载H和弯矩M同时作用的复合加载情况,采用Probe法构建包络面:竖向荷载V保持不变,然后按一定比例施加水平位移和转角,随着水平荷载的增加,弯矩先迅速增加,后沿着包络面运动,连接各加载路径的终点即可获得包络面。图7展示了不同土体强度和不同竖向荷载条件下允许和不允许脱离两种情况的复合承载力包络面,其中sutip是桶基刃角处的土体强度。每个包络面由至少5条加载路径获得,为了在图中清晰表示允许脱离和不允许脱离分别对应的加载路径,此处每个包络面只画出两条对应路径。
不同土体强度条件下桶基在允许脱离时得到的包络面总小于不允许脱离情况,但包络面的形状基本一致,因此采用相似的表达式。已有研究[11,20]建议不脱离时桶基的复合承载力可用式(14)计算。
HH0h*2+MM0m*2+nHH0h*MM0m*=1(14)
式中:系数n决定了包络面的形状, h*和m*分别为描述VH及VM相互作用的函数,采用Vulpe等[9]建议的幂函数
h*=1-υq(15)
m*=1-υp(16)
式中:υ=V/V0,经过拟合得到q=4.6、p=4.4、n=2。以上参数同时适用于允许脱离和不脱离情况,即“桶土”不脱离时,式(14)~式(16)中的V0、H0和M0分别为Vt0、Ht0和Mt0;允许脱离时,分别为Vs0、Hs0和Ms0。图8展示了不同条件组合下公式(14)与有限元结果的对比。虽然脱离条件影响单向水平承载力和弯矩,但其影响已被包含在(H/H0)和h*或者(M/M0)和m*中,所以,式(14)同时适合脱离与不脱离工况,公式计算结果与有限元计算结果吻合。
上述单向与复合承载力计算公式构成了预测脱离条件下桶基承载力的完整流程:确定设计荷载V、H和M,初步选定桶基直径D和长度L;根据式(2)~式(11)确定不脱离时的单向极限承载力,然后由式(12)和式(13)获得允许脱离时的水平承载力和弯矩,单向竖向承载力则不受脱离条件影响;将V、H和M中的任意两个分量代入式(14),得到第3个荷载分量的极限值,若该设计荷载分量小于其极限值,则设计安全,否则需改变基础尺寸。
5 结论
针对风机桶形基础与黏性土的接触条件,改变土体强度和长径比,研究桶侧壁与土的脱离条件对单向及复合承载力的影响,主要结论如下:
1)当sum/kD<0.3时,即使允许脱离,桶基与土体之间也不会形成空隙,允许或不允许脱离得到的承载力几乎相同;而当sum/kD>0.3时,桶基与土体之间形成空隙,破坏模式由“双侧”变为“单侧”,单向承载力最多降低至不允许脱离时的72%。给出了允许脱离时的单向承载力计算公式。
2)桶基侧壁与土体的脱离使复合承载力降低,土体强度越高,降低程度越显著,但归一化表达的复合承载力包络面公式同时适用于允许和不允许脱离条件。提出了考虑脱离条件的桶基复合承载力设计流程。参考文献:
[1] FORESI A, BUGHI S. Suction pile foundation for a PLET subsea structure [C]//Frontiers in Offshore Geotechnics III. Taylor & Francis Books Ltd, 2015: 245-250.
[2] RANDOLPH M F, GAUDIN C, GOURVENEC S M, et al. Recent advances in offshore geotechnics for deep water oil and gas developments [J]. Ocean Engineering, 2011, 38(7): 818-834.
[3] HOULSBY G T, KELLY R B, HUXTABLE J, et al. Field trials of suction caissons in sand for offshore wind turbine foundations [J]. Géotechnique, 2006, 56(1): 3-10.
[4] DING H Y, LIU Y G, ZHANG P Y, et al. Model tests on the bearing capacity of wide-shallow composite bucket foundations for offshore wind turbines in clay [J]. Ocean Engineering, 2015, 103: 114-122.
[5] WANG L Z, WANG H, ZHU B, et al. Comparison of monotonic and cyclic lateral response between monopod and tripod bucket foundations in medium dense sand [J]. Ocean Engineering, 2018, 155: 88-105.
[6] CASSIDY M J, BYRNE B W, RANDOLPH M F. A comparison of the combined load behaviour of spudcan and caisson foundations on soft normally consolidated clay [J]. Géotechnique, 2004, 54(2): 91-106.
[7] VILLALOBOS F, BYRNE B W, HOULSBY G T, et al. Bearing capacity tests of scale suction caisson footings on sand: Experimental data: Report FOT0005/1 [R]. Department of Engineering Science, University of Oxford, 2003.
[8] ZHANG Y H, BIENEN B, CASSIDY M J, et al. Undrained bearing capacity of deeply buried flat circular footings under general loading [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(3): 385-397.
[9] VULPE C, GOURVENEC S, POWER M. A generalised failure envelope for undrained capacity of circular shallow foundations under general loading [J]. Géotechnique Letters, 2014, 4(3): 187-196.
[10] GEROLYMOS N, ZAFEIRAKOS A, KARAPIPERIS K. Generalized failure envelope for caisson foundations in cohesive soil: Static and dynamic loading [J]. Soil Dynamics and Earthquake Engineering, 2015, 78: 154-174.
[11] GOURVENEC S, BARNETT S. Undrained failure envelope for skirted foundations under general loading [J]. Géotechnique, 2011, 61(3): 263-270.
[12] RANDOLPH M F, O'NEILL M P, STEWART D P, et al. Performance of suction anchors in fine-grained calcareous soils [C]//Offshore Technology Conference. Houston, Texas, 1998: 571-579.
[13] GUO Z, WANG L Z, YUAN F, et al. Model tests on installation techniques of suction caissons in a soft clay seabed [J]. Applied Ocean Research, 2012, 34: 116-125.
[14] KUMAR N D, RAO S N. Earth pressures on caissons in marine clay under lateral loads-A laboratory study [J]. Applied Ocean Research, 2010, 32(1): 58-70.
[15] VERITAS D N. Geotechnical design and installation of suction anchors in clay: DNVGL-RP-E303 [S]. Oslo, Norway: 2017.
[16] SUPACHAWAROTE C. Inclined load capacity of suction caisson in clay [D]. Australia: University of Western Australia, 2006.
[17] GELAGOTI F, GEORGIOU I, KOURKOULIS R, et al. Nonlinear lateral stiffness and bearing capacity of suction caissons for offshore wind-turbines [J]. Ocean Engineering, 2018, 170: 445-465.
[18] MEHRAVAR M, HARIRECHE O, FARAMARZI A. Evaluation of undrained failure envelopes of caisson foundations under combined loading [J]. Applied Ocean Research, 2016, 59: 129-137.
[19] 周素靜, 张艳, 王栋. 海底管道沉箱基础的复合承载力包络面研究[J]. 海洋通报, 2019, 38(6): 727-732.
ZHOU S J, ZHANG Y, WANG D. Capacity envelope of caisson foundation for on-bottom pipelines [J]. Marine Science Bulletin, 2019, 38(6): 727-732. (in Chinese)
[20] BRANSBY M F, RANDOLPH M F. Combined loading of skirted foundations [J]. Géotechnique, 1998, 48(5): 637-655.
(编辑 章润红)

