加权奇异值结合极值点包络的变转速轴承微弱故障诊断
张 洲, 张宏立, 马 萍, 王 聪
(新疆大学 电气工程学院,乌鲁木齐 830047)
滚动轴承是旋转机械中使用广泛的重要支撑部件,其健康状况直接影响着整个机械的正常运行。实际中,多数旋转机械都在变转速、变负载的工况下运行,而大部分机械故障都是在轴承工作周期以局部缺陷的形式产生,在后期故障状态加剧,种类增多,极大威胁着设备整体运行的安全性。故障信号具有特征微弱、信噪比低及易被噪声淹没等特点,因此,如何从干扰众多的信号中提取出微弱故障信号是诊断变转速条件下滚动轴承微弱故障的关键[1]。
恒定转速下的微弱故障信噪分离主要是通过一系列特征提取方法结合频谱分析来完成故障的诊断,例如小波变换和变分模态分解(variational mode decomposition, VMD)等方法,都能很好地完成滚动轴承的信噪分离[2-3]。小波分析在分析明显故障冲击信号时较为有效,但其频带特性使小波分析在提取微弱的故障信号较为困难[4]。VMD在经验模态分解(empirical mode decomposition, EMD)基础上提出并有效解决了EMD模态混叠的问题,可以实现信号不同频率分量的有效分离[5]。由于变转速轴承的微弱故障特征常常被强噪声淹没,影响了VMD在变转速下故障诊断的效果和应用。
奇异值分解(singular value decomposition, SVD)具有极好的稳定性和不变性,其分量信号具有线性叠加特性[6]。文献[7]中将SVD分解结合相关峭度特点应用于滚动轴承的故障诊断,有效地提取出轴承弱故障信号。文献[8]将SVD分解结合包络分析方法应用于滚动轴承微弱故障诊断中,准确地分离出轴承的微弱故障特征。然而当背景噪声很强时,微弱故障特征完全被噪声淹没,经SVD分解后不能得到突出的奇异值,因而无法有效提取微弱故障信号。针对以上问题,本文提出一种新的加权奇异值分解(weighted singular value decomposition, WSVD)方法用于提取微弱故障信号,该方法引入周期调制强度(periodic modulation intensity, PMI)指标表征SVD分解后各分量中故障特征的含量,根据该指标可以有效地选取突出的奇异值分量进行叠加得到高信噪比的重构信号。
阶次跟踪[9-10]作为变转速下的信号分析方法可以较好地描述振动信号和转速信号的关系,该方法可以消除转速变化对振动信号的影响,同时也消除了快速傅里叶变化在变转速下频谱模糊的现象。阶次跟踪技术与其他信号提取方法结合能有效诊断变转速条件下机械体的故障[11-12]。阶次跟踪也存在一定的局限性,利用阶次跟踪无法对存在相近频率分量的故障信号进行有效分析导致误诊[13]。文献[14]针对传统阶次跟踪存在插值误差的问题,提出联合时频压缩结合广义解调的方法成功诊断出变转速轴承的故障,实现了“类似阶次跟踪”。文献[15]中提出极值点包络阶次跟踪代替阶次跟踪,结合VMD滤波有效解调出混合扫频信号中调制成分和低阶扫频信号,解决了Hilbert变换结合阶次跟踪解调出两扫频信号阶次差的问题,验证了极值点包络阶次跟踪的先进性。本文使用极值点包络阶次跟踪方法对WSVD重构信号进行分析,完成变转速下滚动轴承微弱故障的诊断。
针对变转速下滚动轴承微弱故障信号特征,本文提出WSVD分解结合极值点包络阶次跟踪的滚动轴承微弱故障方法,该方法将基于PMI的WSVD分解方法引入到滚动轴承微弱故障信号中进行重构去噪,利用极值点包络阶次跟踪方法实现变转速下滚动轴承的微弱故障诊断。仿真和实例结果表明,本文所提方法能有效诊断变转速条件下滚动轴承微弱故障。
1 WSVD信号分解及重构
1.1 SVD信号分解
对于一个实矩阵A∈Rm×n,必定存在正交特征向量矩阵U=[u1,u2,…,um]∈Rm×m和正交特征向量矩阵V=[v1,v2,…,vn]∈Rn×n,使得矩阵A写成
(1)
式中,∑为对角阵,表示为∑=diag(σ1,σ2,…,σl), 其中l=min(m,n),且有σ1≥σ2≥…σl≥0,它们称为矩阵A的奇异值。
在文献[16]中,研究了SVD可以用较为低秩的矩阵近似地替换矩阵A。SVD有此特性,因此在信号处理中成为振动信号去噪的有效工具。对于一个一维信号序列,信号可以通过以下3个步骤实现:
步骤1构造Hankel矩阵
实际应用中,被测信号通常表示为一个时间序列,因此需要构造一个矩阵为SVD分解做准备。文献[17]中有许多矩阵形式,包括循环矩阵,Toeplitz矩阵和Hankel矩阵,其中,Hankel矩阵由于具有零相移特性和类小波特性而被广泛应用。
对于一维的数字信号,x=[x(1),x(2),…,x(N)]其Hankel矩阵的构造可以表示为
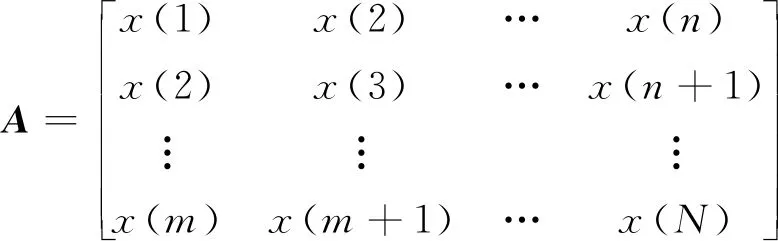
(2)
式中,m=N-n+1。参数m用于确定SVD分解分量的个数,通常小于n。
步骤2信号分解
根据式(1),Hankel矩阵可以写为m个子矩阵Ai相叠加,它满足
A1+A2+…+Am
(3)
式中:ui∈Rm×1为左奇异矩阵U的第i列向量;vi∈Rn×1为右奇异矩阵的第i行向量;Ai∈R1×n对应于原始信号x的奇异分量(singular value component, SC)。
步骤3信号重构
如图1所示,为反对角线重构法。反对角线重构法是将Hankel矩阵A沿矩阵的反对角线求得每条对角线上元素的平均值,由此可得重构信号

图1 反对角线重构法
(4)
1.2 基于周期调制强度的信号重构
处于健康状态的设备其振动能量是均匀的,当发生故障时,由于局部啮合刚度、接触力或瞬态摩擦的变化,振动能量将周期性地变化,从而在从测量信号中产生周期性幅度调制(periodic amplitude modulation, PAM)。实际上,除了故障特征产生的PAM外,振动信号还受到测量噪声和其他干扰的随机调制,使得带有故障的振动信号PAM特征不明显。PMI值(P)表征了故障信号的PAM能量(Eg)与其他干扰信号的能量(Eh)的比值[18]。因此可以利用振动信号的PMI值来衡量信号中是否主要存在故障特征。PMI计算表达式为
(5)
本文采用包络分析识别轴承故障产生的PAM,采用自相关的方法估计PMI值。对于由PAM部分p(t)和随机调制部分n(t)组成的信号x(t),其包络信号a(t)与PAM信号p(t)的包络信号g(t)和随机调制信号n(t)的包络信号h(t)的关系表达式为
a(t)=abs[x(t)+iH(x(t))]=
abs(Ap(t)eiθp(t)+An(t)eiθn(t))=
abs(Ap(t)+An(t))=
g(t)+h(t)
(6)
式中:a(t)为x(t)的包络;H为Hilbert变换;i为虚数单位;Ap(t)为p(t)的幅值;An(t)为n(t)的幅值;g(t)为p(t)的包络;h(t)为n(t)的包络;符号⊗为两信号的卷积。
包络a(t)关于时滞τ的自相关函数为
(7)
令时滞τ为0,得
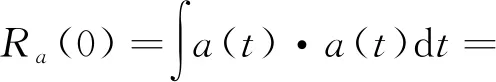
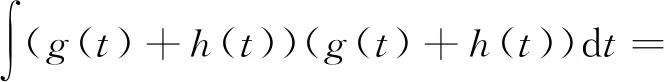
Eg+Eh+2Egh
(8)
式中,Egh为g(t)和h(t)之间得耦合能量。由于g(t)和h(t)通常不相关,Egh为0,因此Ra(0)=Eg+Eh。
由式(8)可知,故障特征引起的PAM与其他干扰信号的随机调制的总能量等于Ra(0)。另一方面,由于PAM是周期性的,其能量可以通过检测包络自相关的相应峰值来获得,假设PAM的周期为T,根据式(9),可以得到Eg=Ra(T)。


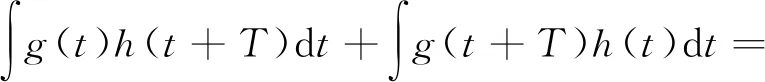
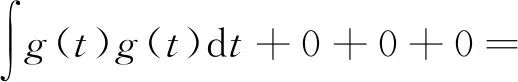
Eg
(9)
根据式(8)和式(9),PMI值对应P可以推导得
(10)
为验证PMI指标能有效衡量变转速信号中调制信号的成分,给定一轴承局部故障信号[19]。仿真信号的采样频率为4 096 Hz,采样时长为1 s,xbe为变转速下的轴承故障信号,如式(11) 所示,固有频率为1 600 Hz,其1~3阶故障特征阶次分别为1.6,3.2和4.8。
(11)
选取不同转速时刻(对应不同的周期T),对不同噪声大小的变转速信号求解其PMI值。图2分别为未加噪声的变转速调制信号与叠加了8 dB,2 dB,0噪声的调制信号,其中信号转速由大变小再变大。

图2 含不同噪声的仿真信号
求取仿真信号的周期信息,所得周期变化图如图3(a)所示。在转速下降的过程中,其周期最小值为0.008 8 s,最大值为0.021 24 s。从中依次选取呈增大趋势的5个周期,依次计算出不同周期下不同加噪信号的PMI值如图3(b)所示。

图3 变转速信号周期变化图及对应PMI值
由图可知,随着变转速信号周期增大,信号的PMI值呈现出下降趋势。同时,在同一周期下,随着信号噪声的加大,其PMI值也呈现出下降趋势,虽然转速的变化会影响信号的PMI值的大小,但其仍然可以较好的衡量噪声在变转速信号中的强弱。因此,PMI指标能较好地衡量出变转速信号中调制信号的含量。
本文对SVD分解后的各分量信号使用截断线性加权函数进行如式(12)所示的加权。设定阈值ε=pmax/2,若某分量信号的PMI值pi小于阈值ε,则将该分量信号认定为与故障信号的相关度过低并将其剔除;若某分量信号的PMI值pi大于阈值ε,认定该分量信号与故障信号存在较大的相关度,将超过阈值ε的分量信号进行重新加权,得到这些信号的权值W(pi),确保PMI值更大的分量信号在重构信号时有更大的权重。然后根据所得各分量信号的权值序列W(pi)进行信号重构,完成信号的重构过程。重构公式如式(13)。
(12)
(13)
2 极值点包络阶次跟踪
基于极值点包络的阶次跟踪方法可以将混合扫频信号中调制成分和低阶扫频信号解调出,是一种有效的变转速工况故障诊断方法。极值点包络阶次跟踪主要分为求取极值点包络和阶次跟踪两部分,其实现过程如下:
步骤1求取极值点包络。求取时域信号的极大值序列,并对其进行三次样条插值得到信号的极值点包络。
步骤2计算极值点包络阶次跟踪。对极值点包络信号进行低通滤波(避免角度域重采样频率过大;避免阶次混叠);结合键相信号,利用阶次跟踪技术完成对极值点包络信号的角度域重采样;对角度域包络线进行FFT,得到包络阶次谱图。
3 基于WSVD与极值点包络阶次跟踪的变转速轴承微弱故障诊断
含有微弱故障的测量信号,其故障特征常常被实验噪声和其他干扰淹没,因此,提取出故障特征明显的故障信号是变转速条件下微弱故障诊断的重点。本文所提方法的流程图如图4所示。
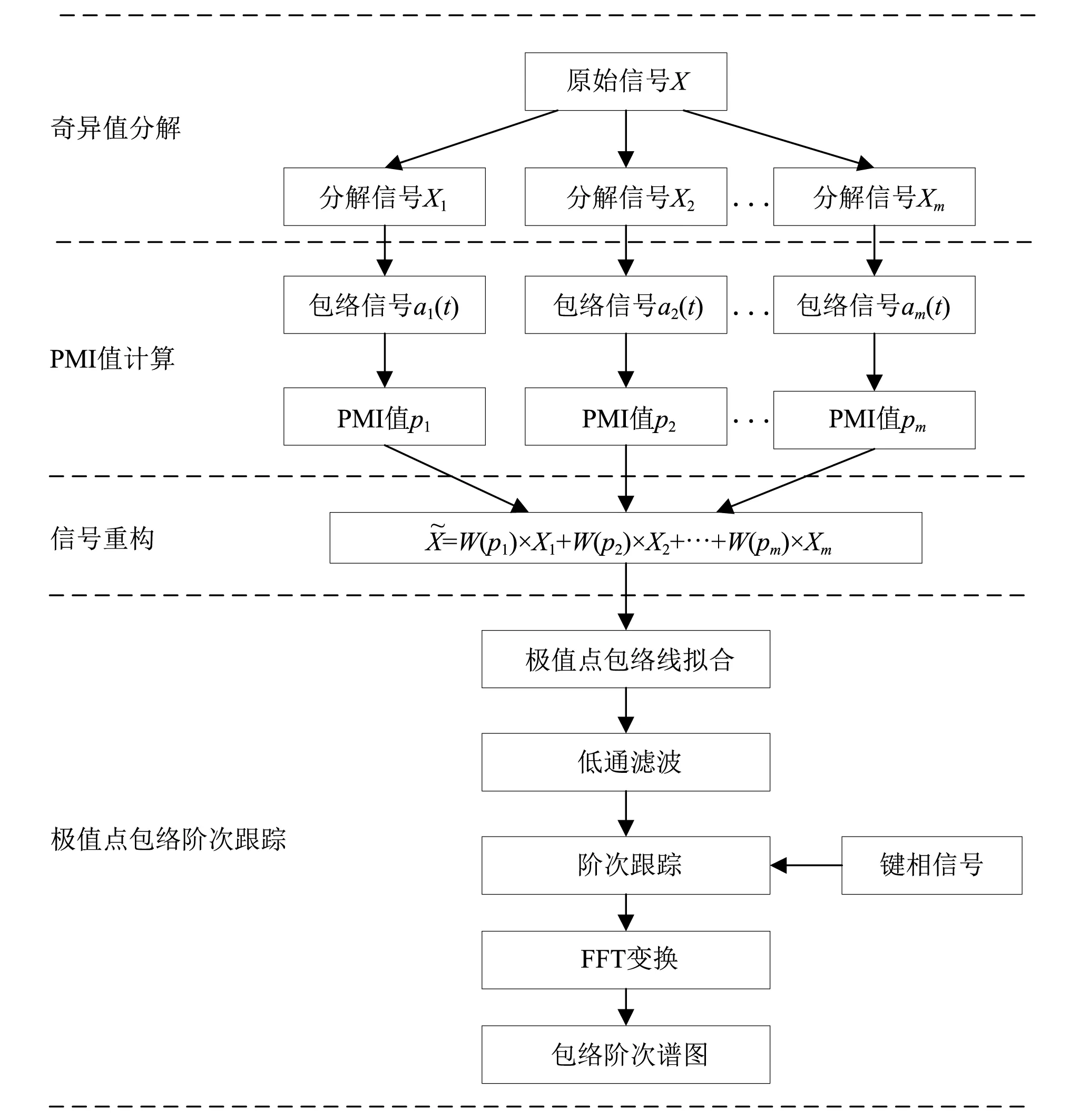
图4 算法流程图
具体步骤总结如下:
步骤1采集轴承的故障振动信号和键相信号,使用SVD分解将故障振动信号分解为m个SVD分量。
步骤2将分解所得的m个SVD分量通过Hilbert变换得到m个包络信号,然后计算出各包络信号的PMI值。


步骤5对包络阶次谱图中的阶次信息进行分析,从而达到微弱故障诊断的目的。
4 仿真分析
为验证本文算法提取变转速轴承微弱故障的有效性,使用由式(11)所得仿真信号进行分析。
如式(14)所示,为模拟变转速下轴承微弱故障信号,在故障信号xbe中引入强度为-8 dB的背景噪声n,得到微弱故障振动信号x,其波形如图5所示。
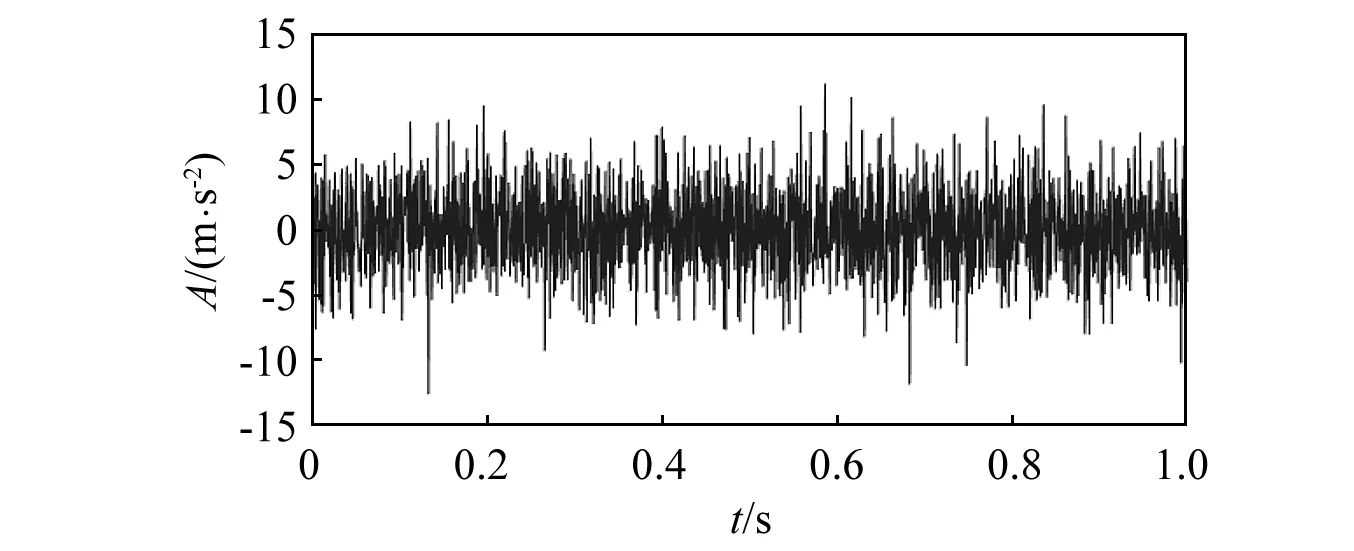
图5 仿真信号
x=xbe+n
(14)
使用SVD分解算法对仿真信号进行处理,设定Hankel矩阵参数m=15,n=4 082,分解所得15个分量信号如图6所示。

图6 15个SVD分量信号
得到的15个分量信号的PMI值,如图7所示,分量1的PMI值p1=pmax=0.24,阈值ε=0.12,且分量1与分量2的PMI值大于0.12且远大于其他的分量,表明分量1与分量2信号与故障信号xbe的相关度更高,与图4中分解得到分量结果相对应,验证了引入PMI值对包含故障特征信息信号选取重构的有效性。加权重构所得信号如图8所示,由图可知,重构信号故障特征明显,与故障信号xbe的相关度非常高,验证了所提WSVD方法具有较好的信噪分离效果。
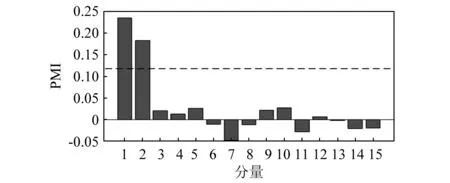
图7 各分量PMI值
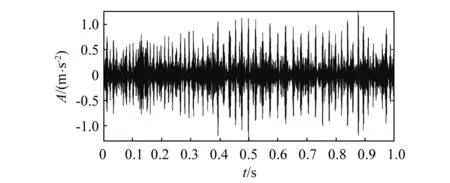
图8 重构信号
使用极值点包络阶次跟踪得到的重构信号的极大值包络,如图9所示。由极值点包络阶次跟踪方法得到的阶次谱图,如图10所示,由图可以看出,故障阶次1.8,3.6,4.8位置明显,噪声被有效剔除,无其他干扰成分出现,验证了本文算法提取变转速下滚动轴承微弱故障的有效性。

图9 重构信号的极大值包络信号
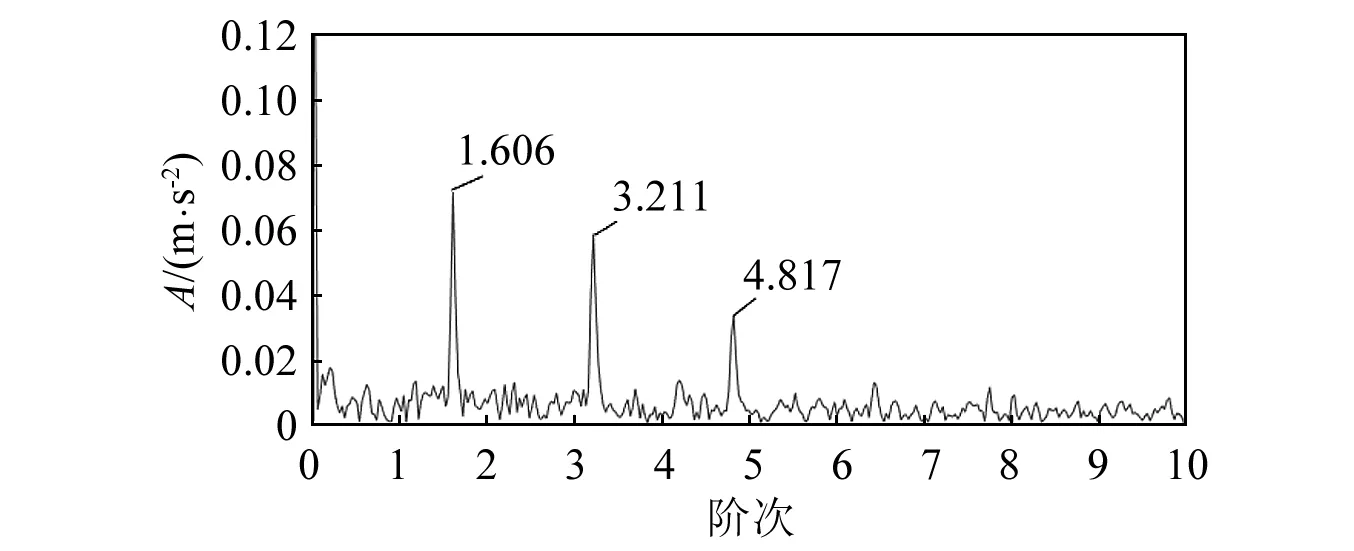
图10 极值点包络阶次跟踪所得阶次谱
为突出本文提出算法的优越性,采用武英杰等使用的VMD结合极值点包络阶次跟踪方法对图5所示信号进行分析。VMD得到的与故障信号相关系数最大的为第4个分量,对其进行极值点包络阶次跟踪,得到的阶次谱图如图11所示。在图11中,虽然出现了设定的3个故障阶次,但图中除了出现较大幅值的噪声干扰外,还出现了1.211和2的干扰阶次,使得设定阶次4.8无法确定。

图11 IMF4极值点包络阶次跟踪所得阶次谱图
5 应用实例
为验证本文方法在诊断变转速下轴承微弱故障的有效性,本文使用了加拿大渥太华大学提供的轴承数据进行分析[20]。该数据在型号为MFS-PK5M的机械故障模拟器上采集,该机械的转动轴由一台交流驱动器控制的变速电机驱动,转动轴左右两侧分别安装了带有内圈故障的轴承和健康轴承,加速度计安装在机械右侧轴承壳上测量故障轴承的振动数据,增量编码器在安装转动轴上用于测量转动轴的转速。
轴承内圈的故障数据在转轴转频从12.5 Hz增加到27.8 Hz状态下采集,采集频率为200 000 Hz,采集时间为10 s,测试轴承的相关参数如下表所示,其中,fr为轴的转频,根据转频、故障特征频率与阶次之间的关系可得,内圈故障的阶次为5.43。截取0.01 s振动信号对本文方法进行验证,振动信号如图12所示。

表1 轴承内圈故障特征阶次

图12 微弱故障振动信号
使用SVD对振动信号进行分解,所得35个分量信号的PMI值如图13所示。由图可知,分量信号中PMI的最大值pmax为1.4,阈值为0.7。按照WSVD的信号重构原则,在进行信号重构时,将PMI值小于0.7的分量信号剔除,将PMI值大于1.25的分量信号按式(15)进行加权重构,得到信噪分离后的重构信号如图14所示。

图13 分量信号的PMI值
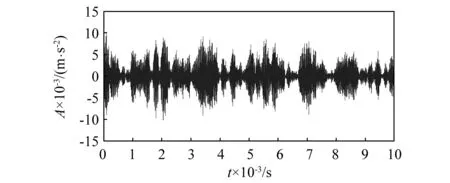
图14 重构信号
(15)
对图14中重构信号进行极值点包络分析,所得包络信号的波形如图15所示,由图可以看出,包络信号可以将重构信号的冲击成分有效凸显。对包络信号进行阶次跟踪,所得包络阶次谱图如图16所示,图中阶次5.323处存在明显峰值,与轴承内圈的故障阶次相近,证明轴承内圈发生故障。

图15 重构信号的极大值包络信号

图16 振动信号的阶次谱图
采用基于VMD滤波结合极值点包络阶次跟踪对图13所示轴承故障信号进行分析,得到分量信号如图17所示,对其进行极值点包络分析和阶次跟踪,得到的阶次谱图如图18所示,阶次5.409虽与轴承故障阶次相近,但存在多个峰值明显的阶次干扰,无法有效判断故障阶次。由此可得,在变转速条件下,本文方法用于诊断滚动轴承的微弱故障优于现有方法。

图17 VMD分量信号

图18 VMD分量信号的极值点包络阶次谱
6 结 论
针对变转速条件下滚动轴承微弱故障信号特征,提出基于PMI的WSVD重构结合极值点阶次跟踪的故障诊断方法,仿真和应用实例验证了本文方法的有效性和优越性。本文主要结论如下:
(1) 提出基于PMI的加权SVD微弱故障信号信噪分离方法。通过仿真和实例分析,该方法可以有效对微弱故障进行有效重构,其分解效果优于VMD方法。
(2) 提出一种基于WSVD与极值点阶次跟踪的变转速滚动轴承微弱故障诊断方法, 并将它应用于滚动轴承仿真和实验数据分析。结果表明, 所提出的变转速滚动轴承微弱故障诊断方法能够有效诊断滚动轴承微弱故障。
(3) 鉴于所提WSVD方法对变转速下微弱故障振动信号的有效特征提取能力,将其应用于变转速下轴承的复合故障分离是进一步需要完成的工作。

