异形支承圆柱滚子轴承结构优化

杨新清，李凌翔，华晓波

(泛亚汽车技术中心有限公司，上海 201208)

1 问题的产生

圆柱滚子轴承因结构简单，且具有较高的刚度，在汽车变速箱中广泛应用。但其抗变形能力差，较小的系统位错量都会产生边缘应力。轴承设计分析时，往往根据传统弹性接触理论计算轴承接触应力[1-9]，从而验证轴承设计是否合理。某汽车变速箱输出端圆柱滚子轴承(图1)开发中出现边缘应力集中现象，从而导致轴承失效(图2)。采用原方法校核得到其接触应力满足设计要求，分析原因可能为弹性接触理论计算方法假设轴承支承均匀，但该轴承实际为异形支承。在此采用有限元法建立轴承实际模型，分析其产生边缘应力集中现象的原因，并提出相应的改进措施。

图1 汽车变速箱输出端圆柱滚子轴承安装位置示意图Fig.1 Diagram of installation position of cylindrical roller bearing at output end of automobile gearbox

2 有限元分析

发动机最大输出扭矩180 N·m,变速箱传动比见表1。变速箱在1挡载荷最大，1挡和主减速齿轮参数见表2。

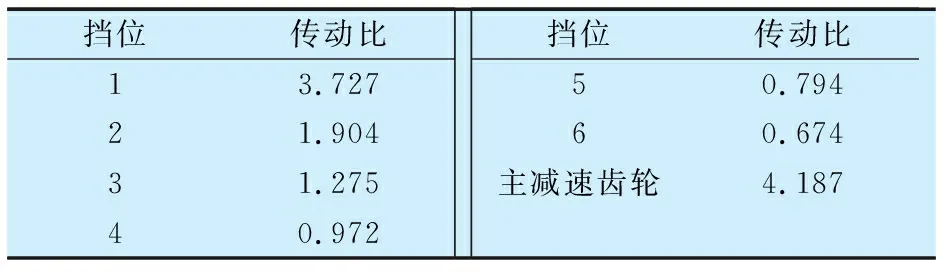
表1 变速箱传动比Tab.1 Transmission ratio

表2 变速箱齿轮参数Tab.2 Transmission gear parameters

圆柱滚子轴承主要结构参数为：内径39 mm,外径68 mm,宽度14 mm,滚子直径8.5 mm，滚子长度15 mm,滚子数量15。内圈和滚子材料为GCr15，外圈材料为S55C中碳钢。额定动载荷为64.86 kN，额定静载荷为71.01 kN。

滚子采用对数修形，对数素线方程为[10]

(1)

Lwe=Lw-2r,

式中：ν为材料泊松比；E为材料弹性模量；Qmax为滚子所受最大载荷；Lwe为滚子有效长度；Lw为滚子长度；r为滚子倒角半径；Fr为径向载荷；Z为滚子数量；对于滚子轴承，1/Jr取4.08。

凸度近似值

(2)

式中：K0为材料常数，对于普通轴承钢，K0=2.81×10-6mm2/N；b为滚子与滚道的接触区半宽；∑ρ为滚子与滚道接触的综合曲率；Dpw为滚子组节圆直径；Dwe为滚子有效直径。

通过上述计算可得1挡时作用在轴承上的径向力Fr为44.43 kN,翻转扭矩为67.19 N·m。

2.1 有限元模型

为准确模拟轴承受力状态，需考虑失效挡位下的动力传递路径、零件刚度、螺栓预紧、配合状态等。考虑1挡时轴承受载最大，模型只留1挡传动相关数模。

建立包含变速器左右壳体、传动齿轮、同步器、轴承板、轴承以及相关的连接螺栓等变速箱整体有限元模型，如图3所示。其中，壳体、轴承板等复杂结构零件采用二阶四面体单元C3D10M划分，对于重点分析的圆柱滚子轴承，需进行网格细化处理，同时考虑滚子沿轴向的修形，采用C3D8I单元，如图4所示。

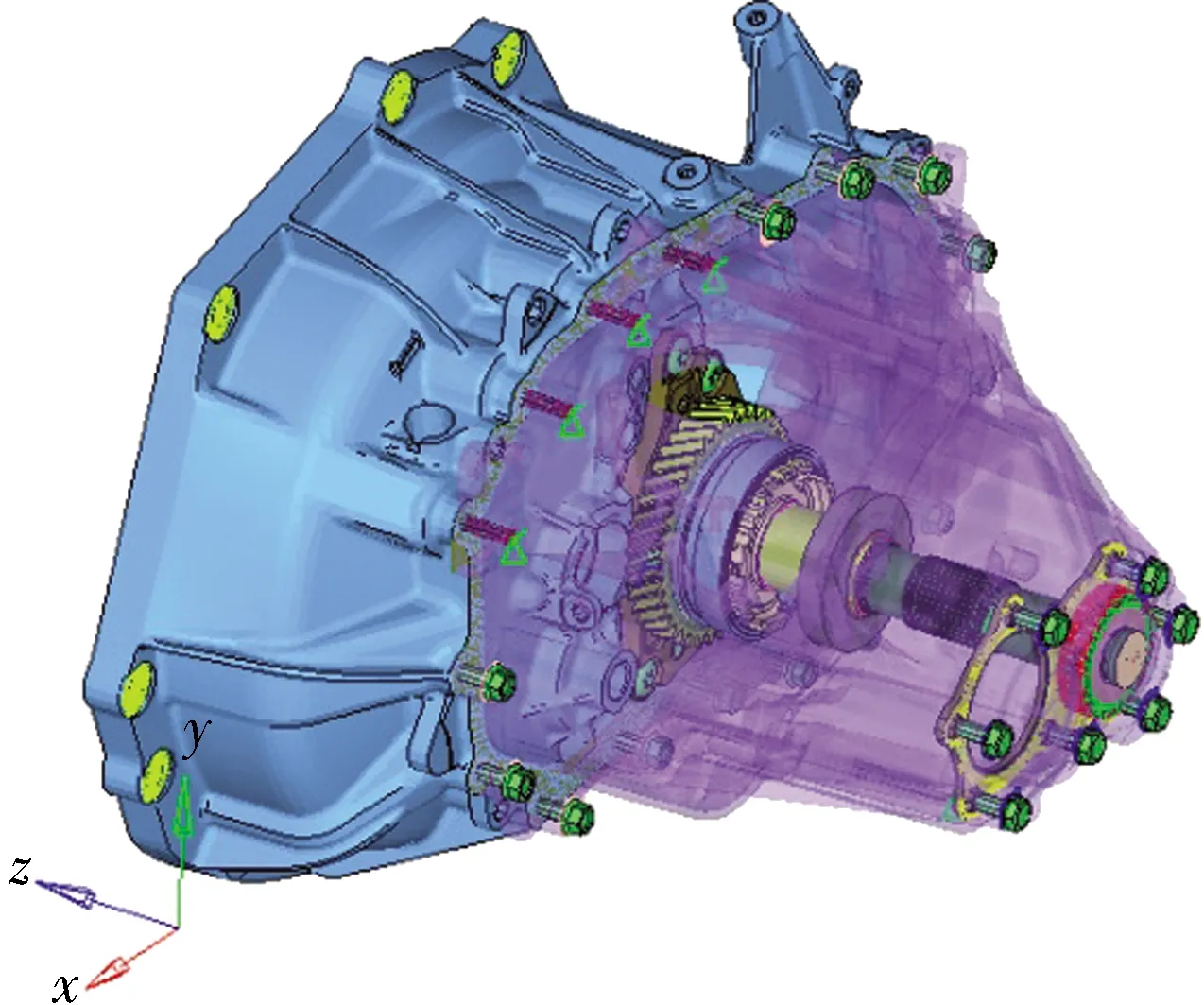
图3 变速箱整体有限元模型Fig.3 Overall finite element model of gearbox

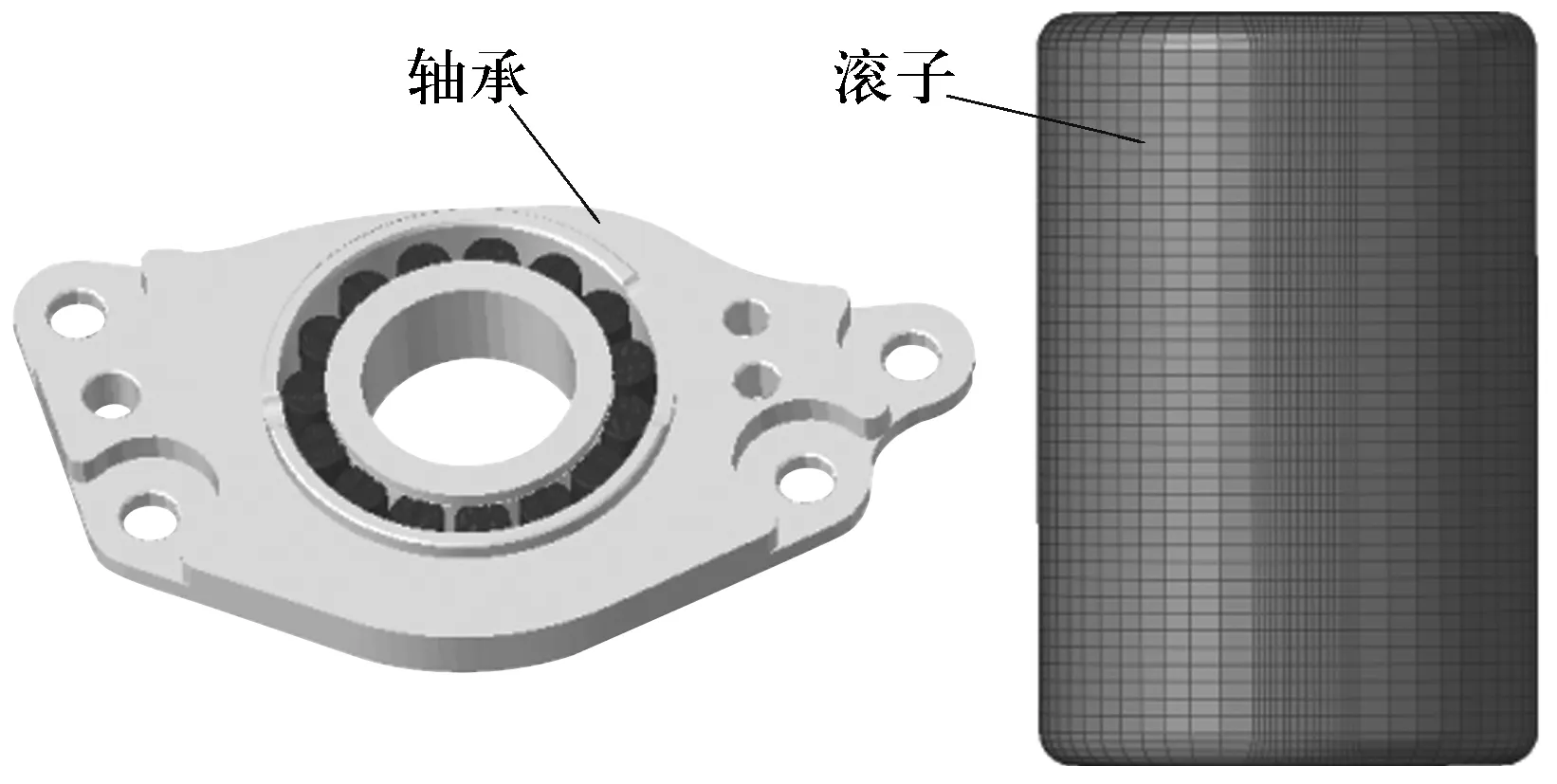
图4 圆柱滚子轴承有限元模型Fig.4 Finite element model of cylindrical roller bearing

通过定义接触对模拟各零件之间的相互传动关系。计算过程中，只考虑某一特定时刻滚子受力，忽略转速的影响，即等效为准静态问题进行分析。滚子与内外圈之间定义接触对时，选择滚子作为从面，滚道面作为主面，摩擦因数为0.03，同时定义相互之间为小滑移Small sliding。考虑轴承板与前壳体的2种极限配合关系：间隙为0.024 mm，过盈为0.002 mm。施加作用在齿轮上的径向载荷Fr=5.86 kN，周向载荷Ft=12.86 kN，轴向载荷Fa=8.12 kN。

2.2 结果分析

轴承外圈滚道轴向截面中心相对初始位置位移如图5所示(间隙和过盈分别对应外圈与前壳体2种配合状态)，由图可知滚道各截面中心基本处于同一位置，说明外圈滚道总体变形一致。进一步分析发现外圈与滚子边缘位置有严重折弯变形，如图6所示，该位置为实际边缘应力失效起始点。对如上轴向各截面进行径向变形扫描，如图7所示，各截面在该处局部变形量径向差异最大为0.05 mm，也就是该处实际折弯变形量。该轴承滚道整体变形一致，轴承错位量很低，局部存在较大变形，从而导致轴承出现边缘应力。

图5 外圈滚道轴向各截面中心相对初始位置的位移Fig.5 Displacement of center of outer ring raceway axial section relative to initial position

图6 滚道折弯变形Fig.6 Bending deformation of raceway

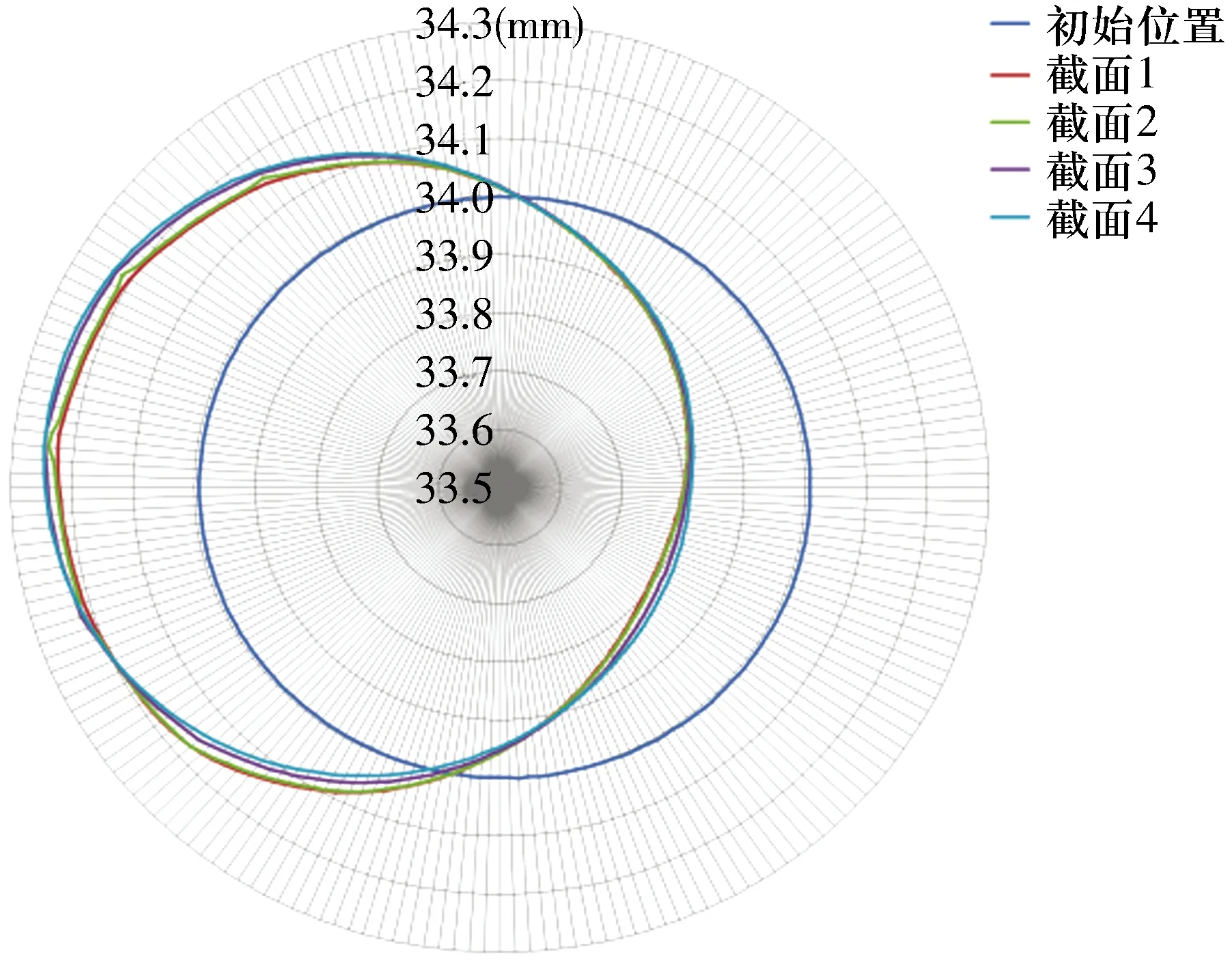
图7 轴承板滚道折弯量计算Fig.7 Calculation of bending amount of bearing plate raceway

为分析轴承滚道局部产生较大变形的原因，对折弯变形位置结构进行分析，如图8所示，轴承板(外圈)安装到前壳体，曲线D与轴承板螺栓安装面平齐，直线E对应壳体C形径向支承边界位置，轴承外圈径向载荷近乎与直线E同处一个平面。前壳体径向支承部位仅为外径面A,外径面B，C不受壳体径向支承。在外径面A处径向支承刚度明显变化，轴承板受壳体反作用力而发生折弯变形。

图8 折弯变形位置结构Fig.8 Bending deformation position structure

3 改进措施及效果

增大轴承自身整体刚度或减小壳体对外圈反向支承刚度都可以减小外圈滚道折弯变形，在轴承板上增加径向加强筋或增大轴承板厚度可提高轴承自身刚度，在轴承板上增加过渡阶梯可减小壳体对外圈反向支承刚度。在此提出以下3种改进方案：1)轴承板单独增加0.2 mm过渡阶梯，如图9所示；2)轴承板端面增加径向加强筋，并增加过渡阶梯；3)轴承板增加轴向厚度，并增加过渡阶梯。

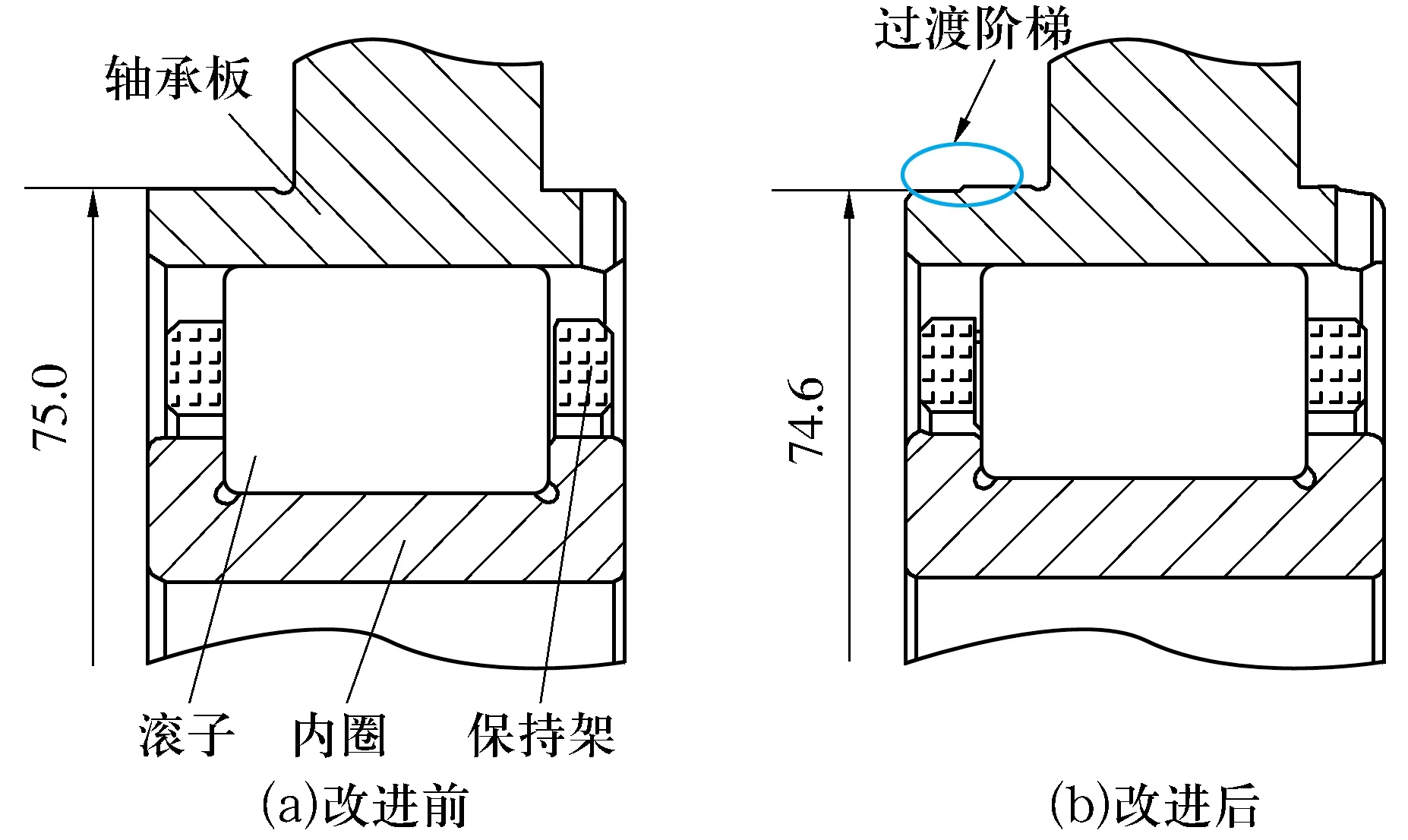
图9 轴承板过渡阶梯特征Fig.9 Features of transition step of bearing plate

通过有限元分析(图10)可得各方案折弯变形如图11所示，由图可知：方案1比原方案变形减小了50%。方案2，3增加轴承板自身刚度会进一步减小变形，但加工难度增大，故采取方案1。

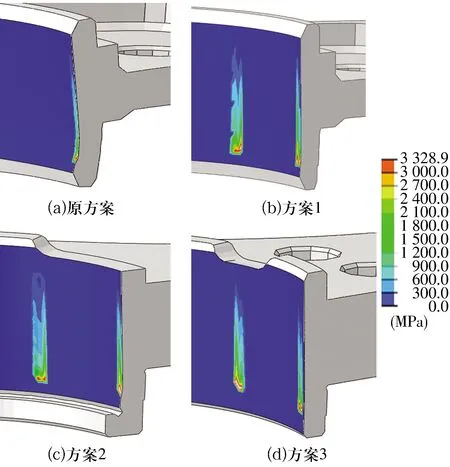
图10 有限元分析模型Fig.10 Finite element analysis model

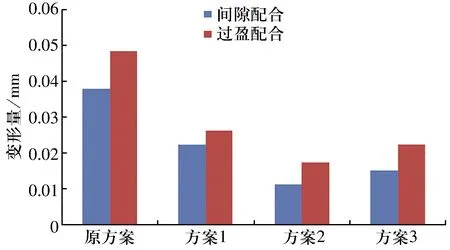
图11 各方案折弯变形对比Fig.11 Comparison of bending deformation of each scheme

对支承结构改进后的轴承进行齿轴耐久试验,变速箱输入扭矩180 N·m，转速4 000 r/min，按最恶劣的1挡进行考核，运行时间为轴承使用寿命。试验后轴承如图12所示，未出现边缘应力集中现象。

图12 轴承试验后拆解示意图Fig.12 Disassembly diagram of bearing after test

4 结束语

对于普通圆柱滚子轴承，通常可采用对数修形来减小边缘应力，而对于异形支承的轴承，仅仅通过滚子修形并不能解决边缘应力集中问题。而通过传统弹性接触理论校核异形支承圆柱滚子轴承接触应力并不准确，应采用有限元分析轴承实际接触情况下的应力分布。