基于递归熵及长短期记忆神经网络的滚动轴承退化趋势预测

崔澜，张宏立，马萍，王聪

(新疆大学 电气工程学院，乌鲁木齐 830046)

滚动轴承是机械设备中极易发生故障的重要部件, 鉴于滚动轴承故障物理模型的不确定性以及智能化处理技术的飞速发展，基于数据驱动的滚动轴承退化趋势预测方法成为一个深具潜力的研究方向[1]，其核心在于状态变化敏感特征的提取，最优退化特征的选择以及预测模型的建立3个方面。

对于敏感特征的提取，文献[2]提取滚动轴承的时域指标并通过主成分分析法构建敏感特征，但该方法增加了人工提取的难度，且易受噪声的影响。文献[3]提出了一种从二维图形上分析非线性时间序列内部动力学特性的递归方法——递归图法(Recurrence Plot，RP)，但递归图仅是对非线性动力学的定性描述，观察起来极不方便。文献[4]在递归图的基础上进行递归定量分析(Recurrence Quantification Analysist，RQA)，从定量的角度对非线性动力学系统进行分析，克服了传统方法对过程平稳的严格要求且对噪声具有一定的抑制作用。文献[5]采用递归定量分析方法，利用递归量指标进行离心泵的故障诊断并得到了较好的结果，但未对故障的预测进行讨论。因此，本文尝试采用递归定量分析方法提取滚动轴承的递归量，并选取最能体现滚动轴承退化趋势的递归量作为滚动轴承的退化指标。

为更好预测滚动轴承的退化趋势，需进行退化状态分割，滚动轴承在完全失效之前需要经历多状态过程，文献[6]利用自动谱聚类的方法将滚动轴承全寿命周期划分为多状态，文献[7]将谱聚类与遗传算法相结合进行时序曲线的聚类。因此，本文利用谱聚类方法对提取的递归量指标进行时序曲线聚类，划分滚动轴承的多种运行状态。

在对滚动轴承退化趋势进行的研究中，文献[8]将递归定量分析与卡尔曼滤波方法结合，但卡尔曼滤波方法需要建立具体的物理模型，对于滚动轴承的非平稳状态而言，建立准确的物理模型比较困难。长短期记忆神经网络[9](Long Short-Term Memory，LSTM)可以处理长期依赖问题，与卡尔曼滤波和马尔可夫模型[10]相比，LSTM不需要预先选择有限个状态即可进行预测，文献[11]利用LSTM进行了故障序列的多步预测且取得了比传统预测模型要好的结果，故本文选择LSTM作为预测模型，对滚动轴承的退化趋势进行预测。

1 基于递归熵的退化指标

1.1 数据预处理

在准确预测滚动轴承退化趋势时，提取最优特征是关键步骤，嵌入定理[12]指出，在确定合适的延迟时间τ和嵌入维数m的情况下，可以从一维混沌时间序列中重构一个与原动力系统在拓扑意义下一样的相空间。对于长度为n的时间序列{x1,x2,x3,…,xn}，重构后的相空间向量为{xi,xi+τ,…,xi+(m-1)τ}，其中M为相空间向量个数，M=n-(m-1)τ,重构后的相空间可表示为

(1)

由此可见，选择合适的τ和m至关重要，本文利用互信息量法确定延迟时间τ并选择虚假临近点法确定嵌入维数m，从而对滚动轴承的原始振动信号进行相空间重构，得到体现系统运行状态的高维特征，并对高维特征进行定性以及定量分析，以挖掘能够体现系统运行状态的信息量。

1.2 递归熵

对重构相空间向量进行定性分析，可得递归矩阵

(2)

式中：Θ为阶跃函数；Yi,Yj为相空间中任意2个点；ε为递归阈值。

采用基于原始时间序列标准差的方法改进递归阈值，具体步骤如下：

1)采用最大相空间尺度的10%[13]确定t1时刻的标准递归阈值ε1。

2)确定t1时刻数据的标准差σ1，得比例系数k=ε1/σ1。

3)确定t2时刻数据的标准差σ2,则t2时刻的递归阈值为ε2=kσ2，以此类推得tn时刻的递归阈值为εn=kσn。

从递归图的点线关系求出系统的递归量[14]，结果见表1。

表1 递归量特征指标Tab.1 Characteristic index of recurrent quantity

(3)

(4)

式中：p(l),p(v)分别为递归图中45°和垂直方向直线的长度；Nl,Nv分别为递归图中45°和垂直方向上长度为l/v的直线的条数；lmin,vmin分别为递归图中45°和垂直方向上直线的最小长度(一般取2)；lmax,vmax分别为递归图中45°和垂直方向直线的最大长度。

1.3 谱聚类

滚动轴承在其全寿命周期内依次经历平稳运行阶段、轻微退化阶段、加速退化阶段和失效阶段，对滚动轴承所处的运行状态进行明确划分，只针对失效阶段前的数据进行预测更具有实际意义。因此，采用谱聚类的方法对退化指标进行时序曲线聚类，以此区分不同的运行阶段。

谱聚类源于图论中的图谱[15]，通过建立各数据点之间的相似度矩阵，将数据聚为不同类别，具体步骤如下：

1)采用全连接法确定所有数据点之间的相似度矩阵wij，即

(5)

式中：xi,xj为任意2个数据点；σ为距离阈值，控制着样本点的邻域宽度，即σ越小表示样本点与距离较远的样本点相似度越小。

2)确定权重矩阵W

(6)

3)确定度矩阵D为

(7)

4)确定量纲一化后的拉普拉斯矩阵L

(8)

5)计算L的特征向量和特征值，将特征值按降序排列得{λ1>λ2>…>λm},取前m个最大的特征值对应的特征向量X=[v1,v2,…,vm]，其中m就是要聚成的类别个数。

6)将X量纲一化得到Y，对矩阵Y按每行为一个数据点，进行k-means聚类，其中第i行所属类就是原来xi所属的类。

由于滚动轴承全寿命周期共经历4个阶段，因此规定谱聚类数目为4。

2 长短期记忆神经网络

2.1 网络介绍

处理非线性时间序列时首选具有时间步的循环神经网络(Recurrent Neural Network，RNN)，但在处理较长的时间序列时，RNN容易造成梯度消失和梯度爆炸的问题，导致更早时刻的数据在训练过程中丢失。针对RNN的缺陷，提出如图1所示的长短期记忆循环神经网络，相对于循环神经网络对系统状态建立的递归计算，3个门控对LSTM单元的内部状态建立了自循环(self loop)，从而使其具有长期记忆功能。

图1 LSTM隐藏层细胞结构Fig.1 LSTM cell structure in hidden layer

LSTM的长期记忆能力可表示为

(9)

式中：xt为当前时刻的数据输入；ht-1为前一时刻的细胞输出；ft为长期记忆c的遗忘比例；it为当前信息输入到长期记忆c的比例；ot为长期记忆c输出到当前状态h的比例。

由(9)式可以求出当前细胞的状态，即

(10)

则t时刻隐含层的状态值ht为

ht=ottanh(ct) 。

(11)

2.2 网络训练

规定输入层数据为提取的递归熵Fo={f1,f2,…，fl}，LSTM输入层数据需满足的格式为(样本个数，时间步，特征个数)，假定递归熵长度为l，时间步大小为s,特征个数为a，则总样本个数为l-s，具体步骤如下：

1)确定训练集样本个数m，则训练集数据输入为

X={X1,X2,…，Xm}，

(12)

X1={f1,f2,…,fs}，

X2={f2,f3,…,fs+1}，

Xm={fm,fm+1,…,fm+s-1}，

若Xm为s×a的二维矩阵，则X为m×s×a的三维矩阵。

2)确定对应的理论输出，即

Y={Y1,Y2,…，Ym}，

(13)

Y1={fs+1}，

Y2={fs+2}，

Ym={fs+m}，

若Ym为a×a的二维矩阵，则Y为m×a×a的三维矩阵。

3)确定测试集输入数据，即

X′={X′1,X′2,…，X′n}；n=l-s-m，

(14)

X′1={fm+1,fm+2,…,fm+s}，

X′2={fm+2,fm+3,…,fm+s+1}，

X′n={fm+n,fm+n+1,…,fm+n+s-1}，

若X′n为s×a的二维矩阵，则X′为n×s×a的三维矩阵。

4)测试集对应的理论输出为

Y′={Y′1,Y′2,…，Y′n}，

(15)

Y′1={fm+s+1}，

Y′2={fm+s+2}，

Y′n={fm+s+n}，

若Y′n为a×a的二维矩阵，则Y′为n×a×a的三维矩阵。

5)将RMS作为误差函数，采用Adam优化器对训练集数据进行训练，训练结束后对测试集数据进行测试。

3 滚动轴承退化趋势预测步骤

结合上述理论分析，所设计的滚动轴承退化趋势预测算法如图2所示，具体步骤为：

图2 滚动轴承退化趋势预测算法流程图Fig.2 Flowchart of rolling bearing degradation trend prediction algorithm

1)选择合适的延迟时间和嵌入维数对原始振动信号进行相空间重构，得到滚动轴承高维相空间向量。

2)对高维相空间向量进行递归定量分析，计算递归熵、递归率、层流性和确定性等退化指标。

3)利用谱聚类方法对各退化指标进行时序曲线聚类，找到最能体现滚动轴承退化趋势的退化指标。

4)谱聚类后划分滚动轴承在运行过程中的各个状态，选择滚动轴承处于正常运行状态数据。

5)将正常运行状态的数据输入长短期记忆神经网络中进行滚动轴承的退化趋势预测。

4 试验验证

4.1 数据准备

为验证本文所提方法的有效性，采用美国辛辛那提大学NSF I/UCR智能维护系统中心提供的滚动轴承全寿命周期振动试验数据，该试验共安装了4套Rexnord ZA-2115双列圆柱滚子轴承，通过PCB353B33加速度计每隔10 min采集1次数据，采样频率为20 kHz，一次共采集20 480个数据。

试验共采集3组数据集，每组数据集都包含4套轴承的振动信号，其中数据集1包含X,Y这2个方向的振动信号，数据集2和3则只包含X方向的振动信号。本文选用数据集2的1#轴承进行验证，该数据集共有984组数据，该组试验起始于2004-02-12T10:32:39，一直监测到2004-02-19T06:22:39，约7天，在该组试验结束后，拆解发现轴承外圈损坏。

4.2 数据分析

对984组数据进行相空间重构，画出系统的递归图，以第1组数据为例，利用互信息量法求得τ=4，利用虚假临近点法求得m=4，标准差σ1=0.073 5，利用最大相空间尺度的10%求得递归阈值ε1=0.904，比例系数κ=12.3，将第1时刻的20 480个数据点分为10等份，每2 048个数据点做一次递归图并求递归量，取10次递归量的平均值作为第1时刻的递归量。以此类推，共可求出984组递归量。将滚动轴承全寿命周期数据平均分为9份，观察9类不同时刻的递归图，画出每个时刻前2 048个数据点的递归图，如图3所示。

由图3可以看出，不同衰退程度的递归特征具有较明显的差别，递归图中黑色区域越大，表明动力学系统中出现的急剧或突然的变化越多。在滚动轴承的正常运行阶段不会出现大面积的黑色区域，随着滚动轴承磨损，会产生大量的冲击信号，导致在滚动轴承最后运行阶段出现大面积的黑色区域。因此，可以用递归量作为反映滚动轴承退化程度的退化指标。

图3 不同时刻的递归图Fig.3 Recurrence diagram at different moments

对递归图进行定量分析得到4个递归量作为评价所选的退化指标，对各递归量进行灰色关联性[16]分析，结果见表2，由表可知改进后递归量(利用标准差改进递归阈值的方法)的灰色关联性指标均要高于改进前。因此，对改进后的递归量指标以及均方根、峭度进行谱聚类。

表2 各退化参数灰色关联性Tab.2 Gray correlation of degradation parameters

选择聚类数目m=4，距离阈值σ=0.1，谱聚类的结果如图4、图5所示。

图4 时域指标谱聚类Fig.4 Spectral clustering of time-domain index

图5 改进后递归量指标谱聚类Fig.5 Spectral clustering of recurrent quantity index after improvement

不同退化指标对滚动轴承全寿命周期不同退化阶段的划分见表3，其中T1～T4表示滚动轴承在不同退化阶段停留的时间。

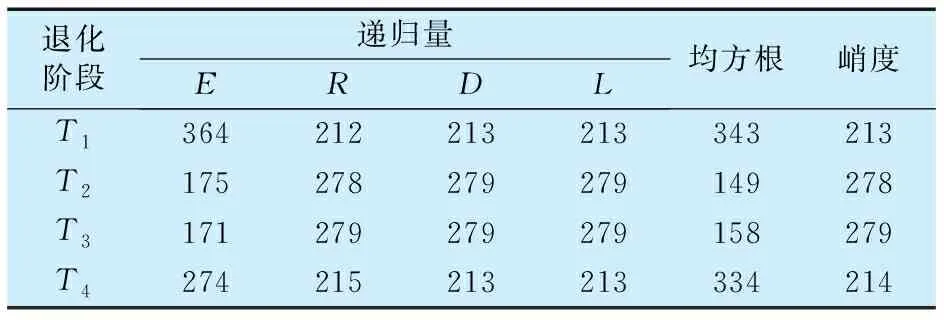
表3 退化停留时刻Tab.3 Degraded residence times

由图4、图5、表3综合分析可知：均方根、峭度、确定性，层流性以及递归率指标均在第490个时刻附近判断滚动轴承进入加速衰退阶段。国内外的研究学者经大量试验表明，该试验中1#轴承的早期故障点在第530—550的时刻区间，由图5d可见，改进递归熵指标判断系统在第539个时刻进入加速衰退阶段，结果更加接近真实情况。

相较于其他指标，选择递归熵作为退化指标可确定该轴承的平稳阶段持续时间比轻微退化阶段长，符合滚动轴承的实际运行情况。对递归熵进行谱聚类时，在第710个时刻处递归熵发生突变，标志着轴承进入失效阶段，而其他指标的谱聚类结果均表明轴承在第760个时刻附近进入失效阶段，但此时相应指标并未发生明显突变。虽然确定性和层流性的灰色关联性高于递归熵，但在进行谱聚类时，递归熵能更好体现轴承的实际运行状态，两者结合能够更加准确的区分轴承的运行状态。

采用长短期记忆神经网路模型进行滚动轴承的退化趋势预测，从图5d可以看出该轴承在运行的第710个时刻进入失效阶段，轴承已受到严重损坏，递归熵值上下波动较大，不具备实际研究意义，故删除第710—984时刻的数据点，利用前710时刻的数据点进行研究。

时间步确定为4，特征值为递归熵，大小为1，一共构成706个样本，取前682个样本作为训练集对模型进行训练，后24个样本作为测试集对模型进行验证，采用Adam优化器，迭代训练120次，LSTM网络结构见表4。将LSTM模型与传统预测模型进行对比，预测结果如图6所示。

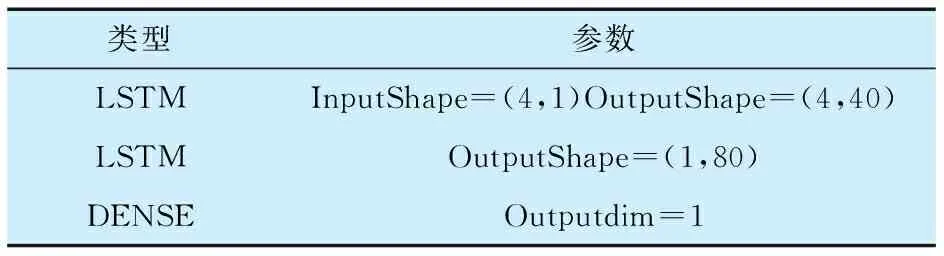
表4 LSTM的网络结构Tab.4 Network structure of LSTM

图6 各模型的退化趋势预测曲线Fig.6 Prediction curve of degradation trend for each model

选择均方误差eMSE和均方根误差eRMSE对预测结果进行评价，其表达式分别为

(16)

(17)

式中：Fi为实际值；Fp为预测值。

由表5可知，相比于其他3种网络模型，LSTM模型的eMSE和eRMSE更低，表明LSTM模型对滚动轴承退化趋势的预测更加有效。

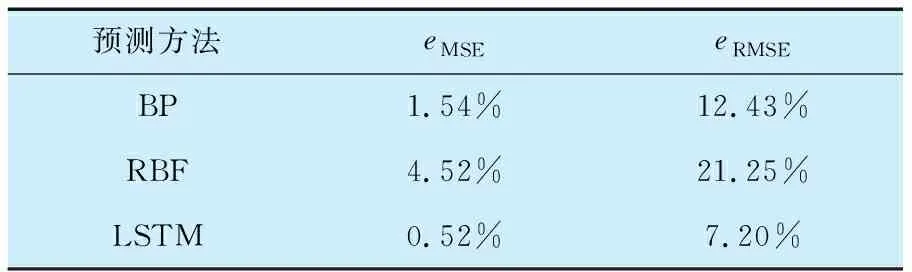
表5 不同预测方法的性能比较Tab.5 Performance comparison of different prediction methods

4 结束语

采用相空间重构法得到滚动轴承的动力学特性并在此基础上进行递归定量分析，选择更加符合滚动轴承实际运行工况的递归熵作为滚动轴承的退化指标。然后，采用谱聚类方法，通过对退化指标的划分，明确了滚动轴承的多状态模式并去除滚动轴承失效点。最后，采用具有记忆功能的长短期记忆神经网络对滚动轴承的退化趋势进行预测，结果表明其预测精度要高于BP神经网络和RBF神经网络，证明了递归熵退化指标结合谱聚类及LSTM神经网络对滚动轴承退化趋势预测的有效性。