超临界二氧化碳涡轮机主轴静压轴承承载特性分析

郑培培，李伦，李济顺，许世钰

(河南科技大学 a.机电工程学院；b.河南省机械设计及传动系统重点实验室，河南 洛阳 471003)

0 引言

超临界二氧化碳(Supercritical Carbon Dioxide，S-CO2)循环是极具发展潜力的新一代发电循环技术。超临界状态下的CO2相较于水蒸气具有更高的能量密度和极低的内摩擦功耗，可极大地提高热循环效率，减小发电装置及配套系统的体积[1-2]。此外，区别于传统水蒸气循环需要消耗大量的水，S-CO2循环属于完全密闭循环，无需额外的气体补给。因此，S-CO2循环发电技术特别适合于太阳能资源充足且干旱缺水的地区，如澳大利亚、非洲及我国西部地区。S-CO2循环发电技术是未来人类能源开发利用的主要研究方向之一。

涡轮机作为S-CO2动力循环的核心部件，其主轴运转的稳定性极其重要，因此对涡轮机主轴的支承轴承提出了更苛刻的要求。目前，气体静压轴承因其运转精度高，无污染，摩擦小，在医疗设备和高精密机床上应用较为广泛[3-4]。国内外学者针对气体静压轴承进行了广泛而深入的研究，目前针对压力和承载力计算主要有以下3种方法：

1)简化的工程计算方法。如文献[5]开发了一种简单的设计方法，以协助轴承的设计或选择，并研究分析了进气孔直径、进气压力、轴承内径对承载力和刚度的影响。文献[6-7]根据空气轴承的特点，结合润滑气体特性，分析了气体静压轴承承载力和刚度等特性。

2)利用有限差分法对静压轴承气膜的雷诺方程进行差分，借助于计算机进行求解。文献[8]将轴承气膜流动简化为量纲一的Navier-Stokes方程，利用牛顿法对其离散并求解，所建立的解析模型为分析高精度旋转气体轴承的动静态性能提供了一种有价值的手段。文献[9]在雷诺方程中增加了流量项，将不同坐标系内的雷诺方程变换成为相同形式，简化了数值计算，并对微分方程离散方法加权余量法、变分求极值法进行了分析讨论。

3)利用有限元方法，构建流体域的三维模型，通过流体分析工具进行仿真计算。文献[10]研究了高速主轴空气静压滑动轴承在不同工况下的刚度特性，针对不同长径比、供气孔直径、供气压力进行了对比分析，结果表明几何结构对刚度有显著的影响。文献[11]采用数值分析法对空气静压轴承气膜压力分布进行了分析，并推算出轴承的承载能力和静刚度的计算公式，为空气轴承板形仪的结构设计和性能分析提供一定的理论依据。文献[12]研究了空气静压轴承的动刚度和阻尼系数，结果表明由于气体的可压缩性，气体静压轴承的动态特性表现出非线性特性，这种非线性特性在超薄气膜间隙和大供气压力条件下尤为显著。文献[13]建立了小孔节流空气静压轴承双向流固耦合数值模拟模型，采用数值模拟法获取了设计参数对承载力和刚度的影响规律，并在气体静压试验平台上对自行研制的空气静压轴承进行静动态特性测试试验验证。文献[14]利用有限体积法分析了静压轴承旋转状态下轴承承载力和耗气量的变化规律，结果表明转速增加引起较为明显的动压效应，动压效应使轴承承载力明显提高。文献[15]结合仿真方法和正交试验方法分析了轴承参数对承载能力的影响，揭示了各个参数对承载力影响的主次顺序。

上述研究方法和文献所涉及的静压轴承均以空气为润滑介质，而对S-CO2为润滑介质的静压轴承承载力和刚度的研究还比较少。此外，由于S-CO2的物理性质与空气差别较大，这给S-CO2作为润滑介质的静压轴承承载力和刚度的研究带来一定的难度。因此，现以S-CO2涡轮机主轴支承静压轴承为研究对象，对比分析了不同参数对S-CO2润滑轴承承载特性的影响。

1 主轴静压轴承结构及工作原理

1.1 支承静压轴承结构

S-CO2涡轮机的汽轮处于悬伸状态，且S-CO2的工作温度为550～750 ℃。本文选用的主轴支承静压轴承可以提高主轴的运转稳定性和刚度，并能够利用低温下的S-CO2完成对主轴的冷却。静压轴承有多种形式，本文选取小孔节流形式的静压轴承(图1)，圆周节流孔数目为8个且呈均匀分布(图1b)。节流孔轴向排数对支承也有一定的影响，因此选取单、双排节流孔静压轴承进行对比分析，所选用轴承的参数见表1。

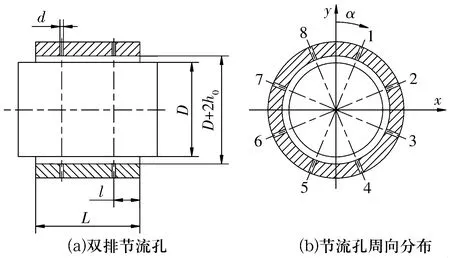
图1 涡轮机径向气体轴承结构Fig.1 Structure of radial gas bearing for turbine

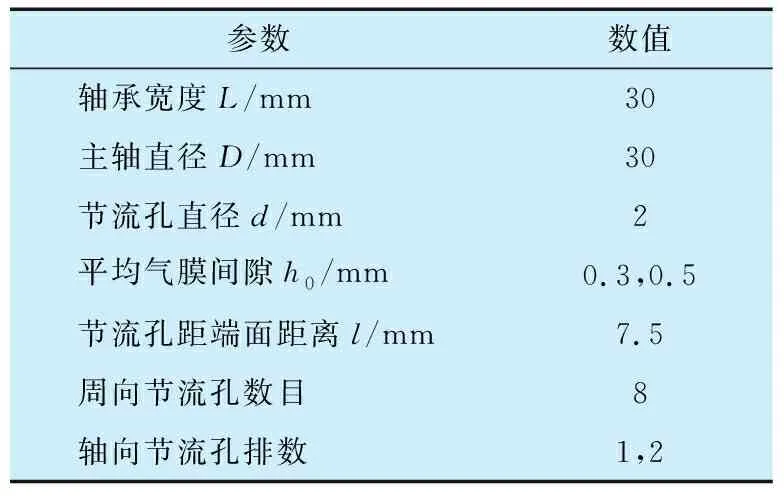
表1 涡轮机径向气体轴承结构参数Tab.1 Structure parameters of radial gas bearing for turbine

1.2 支承静压轴承工作原理

气体支承轴承依靠外部的供气装置在气膜间隙内形成高压气体膜以满足主轴的运转需要，高压气体通过圆周分布的节流孔进入轴承间隙。在空载情况下，轴承四周气膜间隙一致，压力处处相等，形成的承载力相互平衡。在y方向载荷作用下，主轴在y方向将形成偏心，导致y轴上半部分气膜间隙增大，压力减小，下半部分气膜间隙减小，压力增大，上下两部分的压力差使主轴再次达到平衡。

1.3 支承静压轴承承载力和刚度理论

静压轴承的流体域内部流动为稳态流动，根据连续性方程，每个节流孔质量流量为

(1)

βi=pdi/pa,

式中：A为节流孔面积；p0为进气口压力；φ为流量系数；ρ为流体密度;k为气体常数;pdi为出气口压力;pa为环境压力;i为第i个节流孔，其与基准线的夹角为αi。

不考虑其径向y和圆周方向z的流动速度，其内部流体的运动方程为

(2)

式中:p为压力；μ为黏性系数；u为流体轴向流动速度。对其流体域气体流动，有y=0，u=0和y=h，u=0,对(2)式积分可得流体域气体在轴向的速度分布

(3)

式中:y为径向尺寸；h为对应的气膜厚度。

由(1),(3)式可知

(4)

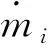
(5)

式中：b为第i等份气膜在圆周方向尺寸；ρa为静压轴承出口流体密度。进一步，流体域轴向在z点的压力可表示为

(6)

针对单个节流进气孔,其形成的压力合力为

Fi=2pdi(L-2l)Rsin(π/n)+

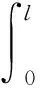
(7)

对(7)式沿圆周方向积分可得整体气膜承载力为

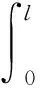
(8)

由(6)式可进一步求得膜承载力为

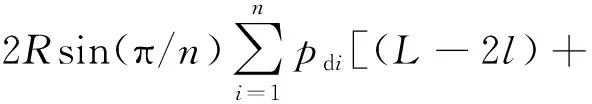
(9)

σ=pa/p0。

根据刚度定义，刚度K为

(10)

式中：Δe为相邻偏心点的偏心增量；W(e+Δe)和W(e)为该2点的承载能力。

2 CFD仿真预处理

2.1 模型建立及网格划分

利用CFD方法分析研究主轴支承静压轴承的特性，主要分析轴承气膜压力、承载力和刚度等特性的影响因素及其变化规律。根据静压轴承的结构参数，在ANSYS Workbench平台上，Design Modeler模块中建立静压轴承的流体域三维模型，如图2a所示。气膜网格划分是数值计算预处理极其重要的环节，网格质量不仅关系到数值计算的效率，也直接关系到计算的精度和准确性。由于静压轴承的气膜间隙远小于轴承的内径和宽度，因此网格划分在气膜间隙位置需要更加的精细。在Workbench meshing模块中对流体域进行网格划分(图2b)，并对进气孔位置网格进行了加密，以满足速度和压力在此处的急剧变化。

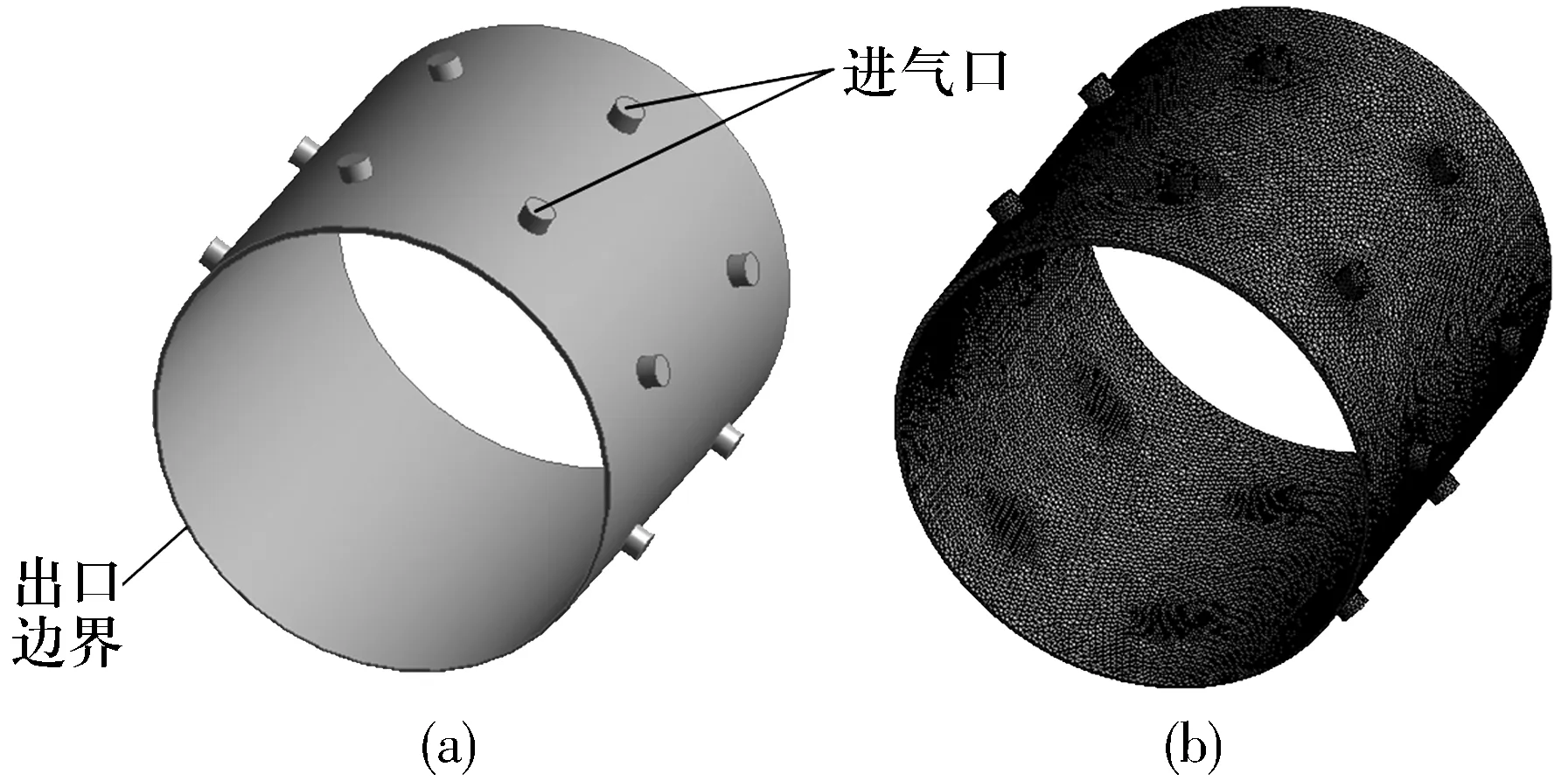
图2 静压轴承整体气膜及流体域网格Fig.2 Integral air film and fluid domain grid of hydrostatic bearing

2.2 S-CO2物性特点

S-CO2与普通CO2相比有更加复杂多变的物性，物性随温度和压力的改变表现出明显的差异性。8 MPa压力下S-CO2的物性随温度的变化曲线如图3所示，由图可知：比热容在临界点附近出现峰值，且临界点前后比热容数值变化较小；密度和导热系数在临界点出现突变，物性数值呈现大幅度减小。黏度是S-CO2重要的物性参数，直接影响到涡轮机主轴的摩擦功耗，因S-CO2兼有气体和液体的双重性质，其黏度接近于普通气体而小于液体，在给定超临界压力下，其黏度在临界点急剧减小，呈现陡直下降特点；随温度的继续升高，在超临界状态其黏度变化较小，8 MPa压力下保持在4.5×10-5Pa·s，与普通状态下CO2的黏度相比减小一半。

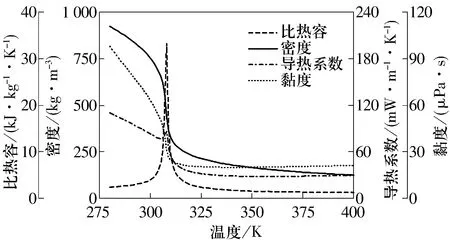
图3 8 MPa压力下S-CO2的物性曲线Fig.3 S-CO2 physical property curve under pressure of 8 MPa

复杂多变的物性易导致静压轴承流体域内仿真结果出现不收敛，因此对S-CO2物性的定义十分重要。本文采用美国国家标准数据库(National Institute of Standards and Technology,NIST)S-CO2气体物性的数据，通过软件对其物性进行拟合，利用Fluent内置函数对物性进行定义。

2.3 数值计算边界条件及仿真工况

因S-CO2气体物性的特殊性，流体在轴承间隙内的流动是十分复杂的三维流动。利用流体分析工具Fluent可对静压轴承内部流体进行相对准确的分析，在数值计算前需做出以下假设：1)气体在气膜间隙方向不流动，即无速度变化；2)忽略惯性力和黏性力；3)忽略主轴表面粗糙度对气膜的影响。

仿真计算湍流模型要根据实际工况选择，针对本文的分析工况，涡轮机主轴的转速为50 000 r/min，轴承内部雷诺数较高，适合选用标准k-ε模型。选择默认的基于压力的求解器(Pressure Based)，求解算法设置为SIMPLEC分离算法。收敛残差决定了计算效果，默认值为10-3，本文设定为10-5。仿真压力入口和出口如图2a所示，其边界条件是：压力设定为绝对压力，入口压力为8 MPa，出口边界设定为大气压力0.1 MPa，主轴偏心率设置为0，0.1，0.2，0.3，0.4，0.5。

3 数值计算结果分析

3.1 流体域压力分布分析

3.1.1 轴承结构和气膜间隙的影响

偏心率为0.5，供气压力为8 MPa时，不同进气结构及气膜间隙下的压力云图如图4所示，由图可知：无论单排还是双排进气结构，压力沿轴向均呈对称分布；当气膜间隙一致时，双排进气结构较单排进气结构的静压轴承流体域压力更高，且更加均匀；在结构一定的条件下，气膜间隙对流体域压力变化影响较为明显，可以看出0.3 mm的气膜压力高于0.5 mm。

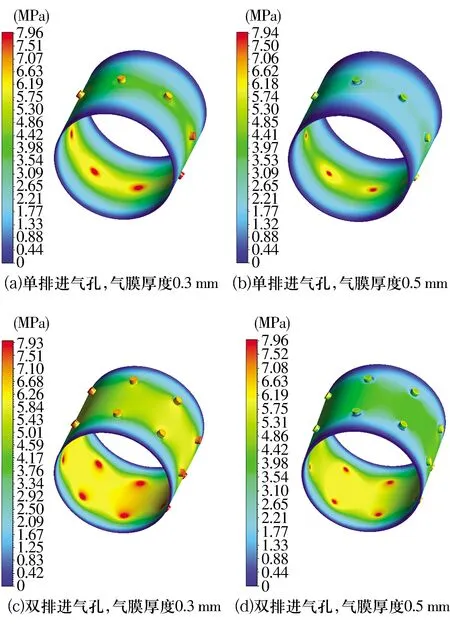
图4 不同进气结构及气膜间隙下流体域压力分布云图Fig.4 Pressure distribution nephograms in fluid domain under different gas supply structures and gas film clearances

3.1.2 偏心率对流场压力的影响

采用图1b中的坐标系，偏心方向为-y方向，进气压力为8 MPa，不同偏心率下的气膜压力分布如图5所示。由图5可知：在涡轮机主轴未受载情况下，主轴偏心率ε=0，流体域中节流孔出口处压力最高，出口边界压力最低；因流体域内气膜间隙一致，气膜压力分布在圆周方向和轴向方向呈现严格的对称性(图5a);随着偏心率不断增大，x轴上方气膜间隙逐渐增大，导致该区域气膜压力变小；x轴下方气膜间隙和气膜压力则相反，对比图5b—图5d可明显看出其压力变化;x轴上下压力差的存在使主轴在偏心方向有更大的承载能力，且偏心率越大，压力差越明显，轴承的承载能力更加突出。

3.2 主轴静压轴承承载力特性

不同进气结构和气膜间隙下静压轴承承载力随偏心率的变化曲线如图6所示,在轴承进气结构一定的条件下，承载力随偏心率的增大而增大，且承载力和偏心率呈现非线性正相关关系。在偏心率较小时，承载力变化较大，随偏心率继续增大，承载力增长幅度逐渐减缓。在偏心率一定条件下，双排进气结构静压轴承承载能力比单排结构更高，且平均气膜间隙较小的静压轴承承载力更高。例如平均气膜间隙0.3 mm的双排进气结构静压轴承承载力较0.5 mm的提高10%。

图6 不同进气结构及气膜间隙下承载力和偏心率的变化关系Fig.6 Variation curves of load capacity with eccentricity under different gas supply structures and gas film clearances

3.3 主轴静压轴承刚度特性

不同进气结构和气膜间隙条件下，静压轴承的刚度随偏心率的变化曲线如图7所示,在相同的偏心率下，双排进气结构的静压轴承刚度明显高于单排进气结构，且平均气膜间隙较小的静压轴承刚度更高。因为偏心率和承载力呈非线性关系，所以刚度随偏心率变化而变化，在偏心率增大过程中，刚度先增大后减小，极值出现在偏心率0.32附近；在偏心率较小条件下，刚度曲线变化梯度较明显，在大偏心率下，刚度曲线下降较缓慢，且刚度的最大值位置并非承载力的最大值。

图7 不同进气结构及气膜间隙下刚度随偏心率的变化曲线Fig.7 Variation curves of stiffness with eccentricity under different gas supply structures and gas film clearances

4 结论

基于Fluent软件对S-CO2涡轮机主轴支承静压轴承进行了数值分析，获得了静压轴承润滑气膜的压力分布云图，揭示了S-CO2润滑条件下的承载力和刚度随偏心率的变化规律:

1)不存在偏心条件下，轴承气膜圆周方向压力均匀分布，轴承承载力为零；气膜间隙一定时，双排进气结构较单排进气结构的静压轴承流体域压力更高。随偏心率增大，气膜间隙减小区域压力增加，气膜间隙增大区域压力减小。

2)在偏心率一定时，双排进气结构静压轴承承载能力比单排结构更高，且平均气膜间隙较小的静压轴承承载力更高；在偏心率不断增大过程中，承载力和偏心率呈非线性正相关关系。

3)双排进气结构的静压轴承刚度高于单排进气结构，且平均气膜间隙较小的静压轴承刚度更高。因承载力和偏心率的非线性关系，刚度和承载力呈现出高度的非线性。刚度在随偏心率增大过程中先增大后减小，偏心率为0.32时出现极值，且极值前的刚度增长梯度高于极值后的减小梯度。